染色机喷嘴缝隙的流动分析与结构优化

Flow Analysis and Structural Optimization of Gaps in Dyeing Machines Nozzle

摘要: 为了提高染色机环形喷嘴的冲击和牵引性能，通过数值模拟分析研究了四种环形缝隙形状(矩形、锥形、锥直形、维多辛斯基形)喷嘴性能的差异，并对锥直形喷嘴结构参数进行了正交实验，还建立了回归预测模型，并利用算法进行了多目标优化，得到了最优结构组合，最后开展了数值模拟验证。结果表明：在不同性能指标下，锥形、锥直形和维多辛斯基形喷嘴均大于矩形喷嘴，且锥直形和维多辛斯基形喷嘴两者性能接近；优化后的锥直形喷嘴在缝隙入口大小为6.00 mm、直段长度为2.00 mm，出口间隙为1.50 mm以及射流角度为40˚时，性能有了进一步的提升。

Abstract: In order to improve the impact and traction performance of dyeing machine annular nozzles, the differences in the performance of nozzles with four annular gap shapes (Rectangular, Conical, Cone Straight, and Vidocinsky) were investigated through numerical simulation analysis, then orthogonal experimental analysis was carried out on the structural parameters of cone-straight nozzles, and a regression prediction model was also established, and a multi-objective optimization was carried out by using an algorithm to get the optimal structural combinations. And build related experi-ments to verify the simulation model. The results show that: under different performance indexes, the conical, conical straight and Vidocinsky nozzles are larger than rectangular nozzles, and the performance of conical straight and Vidocinsky nozzles are close to each other; the optimized cone straight nozzles with a gap inlet size of 6.00 mm, a straight section length of 2.00 mm, a gap outlet size of 1.50 mm and a jet angle of 40˚ provide a further performance improvement.

1. 引言

在当下的实际工程应用中，利用水射流技术的不同类形喷嘴已广泛应用于破岩 [1] 、注浆 [2] [3] 、切割 [4] 、采矿钻井 [5] 、农业 [6] 等多个不同领域，多年来取得了显著的社会效益和经济效益。而不同结构参数的喷嘴具有不同的水力性能，其水力性能直接决定了喷嘴的运行效率。因此，选择合适的喷嘴类形并优化其结构参数，以尽可能地提高性能是非常必要的。

目前研究较多的就是圆管喷嘴，此种喷嘴能提供强大的冲击力，在除锈、清洗等方面有着显著的效果，因此也就成了相关研究的重点。Wen Jiwei等人 [7] 对直锥喷嘴与其他形状喷嘴的结构和水力性能进行了研究，得出了直锥喷嘴的最佳结构，发现其产生的水射流冲击力随其出口直径的增大而显著增大。Luyun Huang等人 [8] 根据超高压水射流除锈喷嘴的工作特点，对喷嘴的水动力特性进行了三维仿真研究，发现靶距和射流角对壁面剪应力大小的影响最为显著。Xin Qiang等人 [9] 提出了一种锥形等离子体射流喷嘴，并通过单因素仿真分析了喷嘴几何形状对射流性能的影响，最后通过正交实验对喷嘴结构进行了进一步的优化。张吉智等人 [10] 对不同结构喷嘴进行了数值模拟，获得了不同结构喷嘴内外壁面的压力场、速度场分布，结果表明相比圆柱形喷嘴，圆锥和余弦形喷嘴射流反推特性更好。还有诸多研究人员对圆管喷嘴进行了研究，分析了出口直径、靶距、工况、形状等影响因素，再通过设计试验、数值模拟、理论计算和实验验证，进一步得出了圆管喷嘴的最优结构参数，以获得最佳喷嘴性能。

不同于常见的圆管喷嘴圆柱射流，还有一类为环形狭缝射流，环形射流泵、喷气(水)织机等设备也均利用了此技术。He Shanshan等人 [11] 为了减少喷气织机的回流现象，设计了一种双喉口的新形主喷嘴结构，通过用负压值和负压区长度来评价回流现象的强度，验证了新结构负压区长度更短，负压值更小，引纬能力更强。Yu Meihong等人 [12] 通过控制变量优化算法对R1234yf喷射器的面积比和喷嘴出口位置在内的几何参数进行优化，以提高其性能。最终结果使喷射器的性能比优化前的夹带率提高了约17%。陈亮 [13] 设计了一种新形的双喷嘴芯串联作用的主喷嘴，并对其引纬流场进行数值模拟和实验分析，发现在合理的压力分配下，新形主喷嘴中气流牵引力能够得到提升，且耗气量得到了有效控制。针对环形射流泵和喷气(水)织机上的环形狭缝射流，诸多研究重心都是在其喷嘴的整体结构，通过设计与优化，使喷嘴性能得到进一步提升。

综上所述，国内外对喷嘴结构设计进行了大量的研究，研究结果表明，通过结构设计和优化可以明显改善喷嘴的性能。在染色机中，环形喷嘴是染色机的核心部件，对染色性能起着至关重要的作用 [14] [15] [16] 。然而，目前对染色机喷嘴结构和形状设计的研究较少。为此，本文通过数值模拟的方法对染色机的喷嘴的环形缝隙结构进行了设计，并对不同环形缝隙形状的喷嘴进行了数值模拟，分析了其性能区别，随后对较优的环形缝隙形状进行优化，获得了较优性能的喷嘴。

2. 建模与仿真

2.1. 模型建立

如图1是染色机圆形喷嘴结构及其计算域，染液经2个入口进入，先经分隔板的缓冲作用，然后进入染液腔内，待染液腔充满染液后，最后从环形缝隙射流而出。在通道内的织物收到高速染液的冲击后，开始运动，同时织物吸附染液，从而实现织物运动的同时进行染色。图中喷嘴直径D为80 mm，喷嘴高度H为80 mm，织物入口直径D_m为30 mm，染液入口直径D_i为15 mm，射流角度α为30˚。

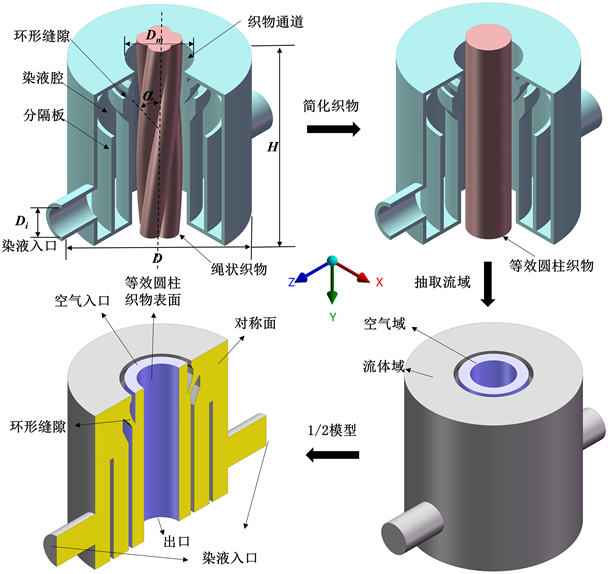
Figure 1. Dyeing machine nozzle structure and calculation domain

图1. 染色机喷嘴结构与计算域

本文利用SolidWorks提取染色机喷嘴的流域。为了更好地研究染液从环形缝隙喷射到织物上的影响，建立了一个带有绳状织物的空气域。但是，为了研究方便，使用刚性圆柱体代替绳状织物 [17] 。因此，计算域如上图中所示，考虑到模型具有对称性，为了减少网格数量和提高计算效率，只选择了一半结构进行仿真分析。

为了研究不同环形缝隙流道形状对染色机喷嘴喷射性能的影响，设计了图2中的四种不同环形缝隙流道形状，分别是矩形、锥形，锥直形和维多辛斯基形。矩形因加工制造方便，是目前染色机喷嘴中应用最广泛的一种缝隙形状，而其余3种缝隙形状鲜有应用到环形喷嘴上的案例。图中缝隙长度l为8 mm，缝隙出口间隙b为2 mm，缝隙入口大小d为4 mm，直段长度l₁为3 mm，其中维多辛斯基形由维多辛斯基曲线方程确定，再通过镜像对称曲线组合形成。

Figure 2. Annular gap shapes

图2. 环形缝隙形状

2.2. 仿真设置

由于染液从环形缝隙喷射到织物上时，会与周围的空气发生动能的交换，因此本文选用广泛运用的k-ε-RNG双方程湍流模型 [18] [19] [20] 和Mixture多相流模型 [21] [22] [23] 。本文用水代替染液进行分析，喷嘴染液入口设置为压力入口为0.1 MPa，水相体积分数设定为1；空气入口设定为0 Pa的压力入口，水相体积分数设定为0；出口设置表压为0 Pa。

本文利用ANSYS-Fluent 2021软件进行计算，采用Coupled稳态算法求解上述控制方程，梯度选择Least Squares Cell Based，压力选择PRESTO，动量、湍流动能和湍流耗散率均为二阶迎风格式，体积分数采用一阶迎风格式，变量残差的收敛准则小于10⁻⁵。

2.3. 评价指标

由于无法直接从数值模拟中得到喷嘴对织物的牵引力，因此本文选取了三个评价指标来反映喷嘴性能，分别是环形缝隙出口速度V_o、等效圆柱织物表面上的最大冲击压力P_max和Y轴方向上的最大剪切力的代数和Δw。环形缝隙出口速度V_o在本文中利用Ansys Fluent软件通过计算其出口的面积加权平均速度计算得出。

为了能够量化不同环形缝隙形状对等效圆柱织物表面产生的冲击效果，在等效圆柱织物表面等间距设置了多条沿着Y轴方向的检测轴线，如图3(a)所示，每条检测轴线上又等距布置了500个检测点，并将所有检测轴线上沿圆周对应点的数据进行求和再对其平均，从而得到一条由平均值组成的等效检测轴线，并以此检测轴线上的数据进行分析。因此，可以从等效检测轴线上的数据得到不同环形缝隙形状对等效圆柱织物表面产生的压力分布，从而得到最大冲击压力P_max。

在本文中，因射流冲击的是圆柱面而不是平板，因此不考虑X与Z方向上的剪切力作用，定义沿Y轴负方向的剪切力，阻碍织物运动；沿Y轴正方向的剪切力，加速织物运动。为了更好的反应不同流道形状的冲击性能，用等效检测轴线上的Y轴正负方向上两个最大剪切力的差——Δw来表示不同流道射流冲击效果：

$\Delta w=W_{\max \_Y+}+W_{\max \_Y-}$ (1)

式中：W_{max_Y+}表示沿Y轴正方向上的最大剪切力；W_{max_Y−}表示沿Y轴正方向上的最大剪切力。

Figure 3. Data collection methods

图3. 数据采集方式

2.4. 模拟结果与分析

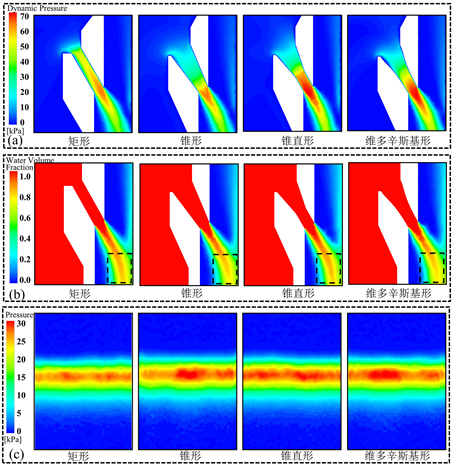
Figure 4. Comparison of different annular gap shapes. (a) Dynamic pressure, (b) Water volume distribution, (c) Pressure distribution

图4. 不同环形缝隙形状对比。(a) 动压，(b) 水相分布，(c) 压力分布

如图4(a)中可以看出，矩形缝隙中的水流的高速区主要集中在缝隙中心，而锥形和维多辛斯基形的高速区集中在出口处，而锥直形由于缝隙流径在直段l₁突然变化，使得直段处的水流受到挤压而导致速度迅速加快。从图中也可发现，由于水流在此压强下为不可压缩流体，因此可以发现锥直形和维多辛斯基形缝隙出口速度明显大于矩形和锥形，出口的高速区长度也更长，且两者的V_o接近，分别为11.48 m/s和11.49 m/s。

而从图4(b)的水相分布来看，经四种不同环形缝隙形状的射流在冲击到等效圆柱织物表面前，其中心水相体积分数无明显区别，但在冲击后，锥形和维多辛斯基形的射流其中心的水相体积分数较矩形和锥直形有所下降，说明在射流发生了扩散，损失了动能。

从图4(c)压力分布来看，锥直形喷嘴在等效圆柱织物表面造成的冲击压力分布均匀，矩形、锥形和维多辛斯基形都有不同程度的压力分布不均的现象，这是因为一方面，水流从缝隙射流出后会发生扩散，此时射流的形态会发生变化，另一方面环形射流冲击到圆柱面上后会互相作用，导致冲击压力分布不均匀。从P_max的具体数值来看，矩形的P_max为26.49 kPa，锥形和维多辛斯基形接近，分别为27.71 kPa和27.91 kPa，而锥直形P_max最大，较矩形提高了6.15%，达到了28.12 kPa。

从图5中可以看出，四种喷嘴在等效圆柱织物表面产生的剪切力在Y负方向上无明显区别，均有剪切力分布不均的现象出现。而在Y正方向上，锥直形喷嘴产生的剪切力分布较均匀，而矩形、锥形和维多辛斯基形喷嘴产生的剪切力分布有局部集中的现象，这是因为冲击压力分布不均导致剪切力分布也产生了差异。

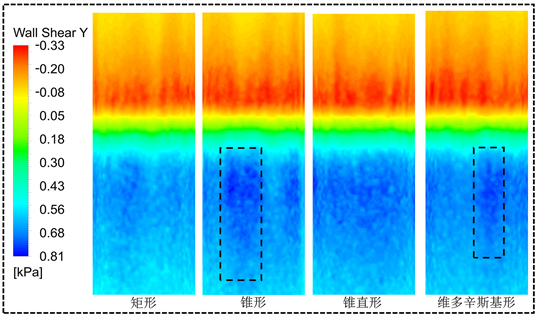
Figure 5. Y-direction wall shear stress distribution cloud

图5. Y方向壁面剪切力分布云图

从图6可以看到，Y负方向上，剪切力大小各形状喷嘴之间接近；Y正方向上，矩形喷嘴产生的剪切力最小，锥形、锥直形和维多辛斯基形喷嘴产生的剪切力互相接近，计算Δw的值可知，矩形喷嘴的Δw为0.41 kPa，锥形、锥直形和维多辛斯基形喷嘴的Δw对比矩形喷嘴均提升了约8.90%。

综上所述，锥直形喷嘴性能优于矩形、锥形和维多辛斯基形，造成的射流冲击力更大，且受力分布均匀，可使织物运动平稳，因此下文以锥直形喷嘴为对象进行下一步分析。

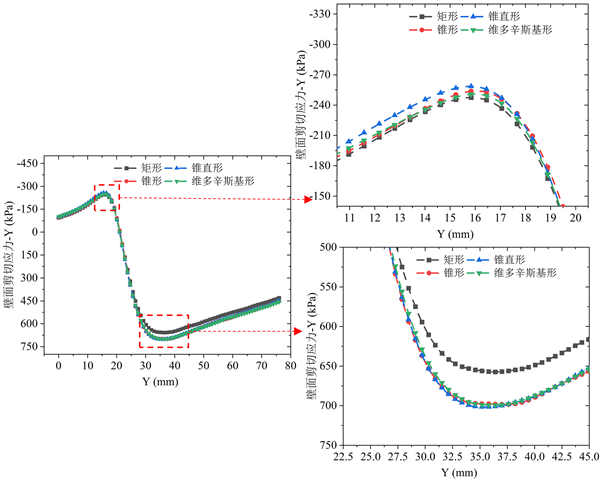
Figure 6. Y-direction wall shear stress distribution curve

图6. Y方向壁面剪切力分布曲线。

3. 喷嘴优化

3.1. 正交实验研究与分析

因锥直形其结构参数的变化极易影响射流性能 [24] ，因此建立正交实验，来研究锥直形结构组成在缝隙整体长度l不变的情况下，缝隙入口大小d、直段长度l₁、出口间隙b以及射流角度α对喷嘴性能的影响。建立的水平因素表如表1所示，4个因素加1个空白对照组共5个因素，根据正交设计原理，5因素4水平需进行16次实验，记作L₁₆(4⁵)。16次实验结果如表2所示。

Table 1. Test factors and levels

表1. 试验因素及水平

Table 2. Results of orthogonal experiments

表2. 正交实验结果

极差分析具有计算简单，结果直观等优点 [25] ，因此采用极差分析来处理上述实验数据，其计算公式如下：

$R_j=\max \left\{{\text{T}}_{j1},{\text{T}}_{j2},{\text{T}}_{j3},{\text{T}}_{j4}\right\}-\min \left\{{\text{T}}_{j1},{\text{T}}_{j2},{\text{T}}_{j3},{\text{T}}_{j4}\right\}$ (2)

式中，T_jm为第j列因素m水平的实验指标平均值，R_j为第j列水平因素变化从而影响评价指标幅度的大小。其各指标下的极差分析结果如表3所示。以V_o为指标时，锥直形缝隙形状不同结构参数对V_o的影响先后顺序为出口间隙b、直段长度l₁、射流角度α、缝隙入口大小d。T_C1 > T_C2 > T_C3 > T_C4，说明V_o随着间隙的增大而减小，以V_o为指标时，其最优组合为入口大小4 mm，直段长度3 mm，出口间隙1.50 mm，射流角度25˚。

Table 3. Range analysis

表3. 极差分析

以P_max为指标时，锥直形缝隙形状不同结构参数对P_max的影响先后顺序为射流角度α、出口间隙b、直段长度l₁、缝隙入口大小d。一般研究当中射流角度的改变需要控制靶距，但由于染色机喷嘴的织物通道的直径是由所染织物的克重决定的，而且实际运行过程中织物会在织物通道内摆动 [26] ，造成靶距实时发生变化。因此，为了便于研究，在仿真中假设织物一直处于喷嘴中心，即不考虑因射流角变化造成靶距的变化。因此在以P_max为指标时，射流角度α的影响最大，且随着角度的增大，P_max也随之增大。以P_max为指标时，其最优组合为入口大小4 mm，直段长度3 mm，出口间隙2.00 mm，射流角度40˚。

以Δw为指标时，锥直形缝隙形状不同结构参数对Δw的影响先后顺序为射流角度α、缝隙入口大小d、出口间隙b、直段长度l₁，其最佳水平组合为入口大小4 mm，直段长度3mm，出口间隙1.75 mm，射流角度40˚。

通过极差分析，发现在不同指标下，锥直形喷嘴的最佳结构参数组合有所不同，这是因为缝隙出口速度V_o最大时，最大冲击压力P_max与最大剪切力代数和Δw都不是最大值，而且P_max影响喷嘴对织物的上染效果，Δw影响喷嘴对织物的牵引能力，因此确定锥直形喷嘴的最佳结构参数时，以P_max与Δw这两项指标作为优化目标。

3.2. 建立回归预测模型

由于涉及以P_max与Δw这两项指标作为优化目标，因此需先建立其各自的回归预测模型。目前许多数据分析软件具有能够基于多种方式对数据进行分析、归纳、预测、调整、改进等功能，因此本文利用Minitab软件对16组数据进行回归预测模型的建立。考虑到锥直形缝隙形状的四个参数对不同评价指标的影响，以及正交实验的分析，得知四个影响因素之间可能存在交互作用，因此采用二次多元回归模型，分别对P_max和Δw建立预测模型，得到如下模型：

$P_{\max }=-38.29-0.2228l_1+26.34b+1.2973\alpha -6.07b^2$ (3)

$\begin{array}{c}\Delta w=-523.6+11.57d+12.17l_1+495.6b+28.5\alpha \\ -83.1b^2-0.2069{\alpha }^2-3.68d\cdot l_1-6.938b\cdot \alpha \end{array}$ (4)

在正交实验各因素的水平范围内，随机选取了8种参数组合来验证模型，其结果如表4所示，其中P_max平均误差为1%，最大误差3.48%；Δw平均误差1.24%，最大误差为2.64%。两者其平均误差均小于2%，表明预测模型精度较高，可以用于求解喷嘴最佳参数组合。

Table 4. Regression prediction model validation

表4. 回归预测模型验证

3.3. 多目标优化

得到P_max与Δw的目标函数后，本文利用利用NSGA-II算法进行多目标优化。NSGA-II算法的种群数量为200，迭代次数为1000次，交叉比例为0.7，变异比例为0.2，Pareto前沿比例为0.15，并规定了缝隙入口大小d上下边界范围为3 mm~4 mm、直段长度l₁范围为2 mm~5 mm和出口间隙b为1.50 mm~2.25 mm，以及外部参数射流角度α范围为25˚~40˚。经过计算，得到了如图7(a)所示的包含30个解的Pareto前沿最优集合。

由于实际应用中，需从Pareto前沿最优集合中选择一个最优解来作为最终结果。这就需要对多目标进行决策过程，本文中采用了基于熵权法的TOPSIS方法对Pareto前沿最优集合中的解进行客观赋值后进行评分，以此来得到其最优解。经过计算，得出最大冲击压力P_max权重为0.325，最大剪切和Δw权重为0.675，其30个解各自所得评分如图7(b)所示，其中第26号参数组合评分最差为0，第15号最好评分为1，其对应的结构参数为：缝隙入口大小d为6.00 mm、直段长度l₁为2.00 mm，出口间隙b为1.50 mm以及射流角度α为40˚。

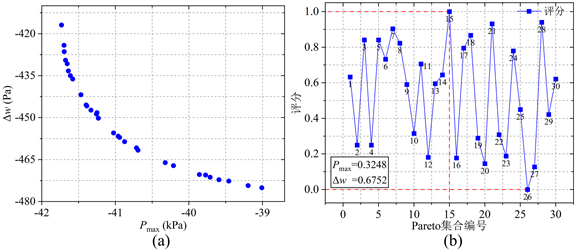
Figure 7. The Pareto set and its score: (a) Pareto set, (b) Score

图7. Pareto集合及其评分：(a) Pareto集合，(b) 评分

3.4. 优化结果对比

Table 5. Optimization before and after comparison

表5. 优化前后对比

利用数值模拟对优化前后的锥直型喷嘴分别在不同入口压力下进行了验证，结果如表5所示。优化后锥直型环形缝隙的出口速度V_o对比优化前提升了6.60%，而优化后锥直型喷嘴最大冲击压力P_max对比优化前有40.46%的提升幅度。最后，优化后锥直型喷嘴的Δw也较优化前提升了3.12%。总的来说，优化后的锥直型喷嘴性能有了进一步的提升。

4. 总结

本文探讨了不同环形缝隙形状(矩形、锥形、锥直形、维多辛斯基形)喷嘴冲击和牵引性能的差异。此外，还对锥直形喷嘴的结构参数进行了优化，以获得更好的性能。得出以下结论：

1) 在不同性能指标下，锥形、锥直形和维多辛斯基形喷嘴均大于矩形喷嘴，且锥直形和维多辛斯基形喷嘴两者性能接近。

2) 对锥直形喷嘴结构进行了正交实验设计，分析发现不同性能指标下，出口间隙b和射流角度α的影响程度最大。

3) 通过建立回归预测模型与利用NSGA-II算法对锥直形喷嘴进行多目标优化求解，并利用基于熵权法的TOPSIS方法得到了最优组合为缝隙入口大小d为6.00 mm、直段长度l₁为2.00 mm，出口间隙b为1.50 mm以及射流角度α为40˚，并利用数值模拟进行了对比，发现优化后喷嘴性能得到了进一步的提升。

综上所述，对喷嘴环形缝隙的改进与优化能够有效提升染色机喷嘴的牵引性能，提高整机生产效率，降低能耗，进一步推动印染行业绿色发展。

基金项目

浙江理工大学2022年省教育厅一般科研项目(项目编号：Y202250589)。