1. 前言
农村农业经济的可持续发展对于我国经济和社会稳定发展具有重大意义,这使得其研究广泛而深刻。但从农村农业经济发展的研究中,不难发现,对于其经济发展的影响因素分析,多数学者停留在理论分析上 [1] ,而鲜有数据实证分析农村农业经济发展的研究。这一部分原因是我国地域辽阔,东西部地区农村经济发展基础与发展水平不同,且影响农村农业发展的因素众多,无法将其逐个列举进行分析,另一方面是因为我国有关农村地区数据调查的缺失,其主要表现在家庭金融资产、居民收入等敏感话题上,使得对于农村地区经济发展研究无法通过数据模型进行分析 [2] 。
二十世纪八十年代以来,农村经济可持续发展成为世界热议的话题。而我国自进入新常态以来,更加重视调结构、稳增长的经济发展,不再是一味地追求经济总量的增长;更加注重经济结构的对称态及在对称态的基础上的可持续发展,而不仅仅是GDP总量、人均GDP增长与经济均衡产出最大化。农村经济新常态是在找准经济增长点、实现农村经济结构对称态的基础上实现经济高速可持续发展,这在追求长期经济稳态增长的索罗–斯旺模型中得到了很好的诠释。索罗–斯旺在构建新古典经济增长模型时,将资本与技术作为经济增长的主要因素,而将其他影响经济增长的变量均视为外生变量,并给予诸多严苛的假设条件,虽在当前社会看来其前提假设条件难以满足且过于严格,但对于研究我国农村地区经济发展仍有较大的借鉴意义 [3] 。货币主义学派的代表人物弗里德曼将经济的发展不仅仅归功于资本与劳动人口,而更多地将货币市场因素与资本市场因素作为经济发展的重要因素,例如资本市场债券利息等。这其实是过度强调金融市场发展对于经济的作用,而冲淡了实体资本对于经济发展的贡献。这显然与我国十九届五中全会提出的强调“全面振兴实体经济,培育壮大新动能,防止产业‘空心化’和经济‘脱实向虚’”的理论,且与我国当前农村地区金融市场基础薄弱,货币影响传导机制较弱的发展现状相违背 [4] 。
在已有的文献中,许多国内学者通过对农村农业发展提出自己的看法与见解,但未尝有分析农村地区农业发展影响因素的案例 [5] 。事实上,通过应用索罗–斯旺模型,假定资本与劳动人口作为农村地区经济发展的解释变量,从国家统计局与中国统计年鉴的数据上看,这可能具有一定的相关性。事实上,通过观察我国农村地区的经济发展状况就可以发现,我国农村农民人均收入自1984年至2019年以来,由人均3321元上涨到人均16,021,增长了4.82倍;同样1984~2019年间我国第一产业产出总量平均每年实际增长3.22%,产出总量增长3.02倍,农村地区人均资本量也从1984年的790元,上涨到2019年的2693元,共增长3.42倍;但第一产业从业人员数量从1984年的37,746人,下降至19,445人,减少了0.94倍。这也从另一方面解释了我国农村地区经济发展中的影响因素项,存在技术增长这项解释因素,符合我国农村经济发展的实际情况 [6] 。
但对于技术增长这项影响因素的衡量上,在已知文献的研究中,我国国内诸多学者并未给出直接衡量农村地区技术增长的指标,更多是借助已有数据侧面替代技术发展,并将其作为解释变量进行分析经济增长的影响因素。本文借助古典凯恩斯主义的两部门模型,并借助增长核算方程,通过对农村地区经济发展影响因素作出基本假设,并在其基本假设的基础上,将技术增长作为刨除资本与劳动力因素所带来的经济增长贡献外的影响贡献进行衡量,这在本文的理论分析部分将进行详细阐述。
本研究认为农村地区经济增长取决于劳动力人口因素与农村地区资本存量,而三者之间的影响关系与影响路径需得到实证与分析解释,唯有如此才能找到农村地区经济增长的正确影响路径 [7] 。
基于这一目的,本文在理论分析的基础上,分析当前我国农村地区产业发展现状,使用1984~2019年中国国家统计局数据与中国统计年鉴数据作为数据来源,运用时间序列分析方法研究农村地区经济增长同农村地区劳动力人口因素与资本存量增长的关系,并以此为根据提出对农村地区经济可持续发展的对策与建议。文章第二部分将对本研究的计量模型建立、数据来源和分析方法做出具体说明;第四部分将对本研究所使用的计量模型进行实证分析,运用单位根检验(Unit Root Test)、协整检验(Cointegration Test)、格兰杰因果关系检验(Granger Causality Test)、误差修正模型(Error Correction Model)和脉冲响应分析(Impulse Response Analysis)对其影响路径进行实证分析,并将在文章的最后部分对实证结果进行进一步解释说明,提出相关建议,揭露其政策含义,给出其实际支持的最终结论。
2. 农村地区可持续发展理论分析
索罗–斯旺认为经济增长不应该只局限于资本的广化,更应该追求资本的深化。所谓资本广化是指资本的增长率同劳动力的增长率相同,从而使得两者的比率相同。而资本深化则是资本的增长率快与劳动力的增长率,从而使得人均储蓄或人均资本量增加 [8] 。而根据我国统计年鉴数据表明,结果见图1,我国农村第一产业劳动力人口多年呈负增长,最新数据显示,2019年我国第一产业劳动人口仅为19,445人,这数据仅是1987年我国第一产业劳动人口的51.5%,另一方面我国第一产业生产总值的变动呈现上升趋势,1984~2019年间共增长3.02倍。
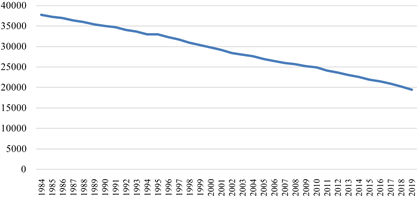
Figure 1. Number of employees in the primary industry from 1984 to 2019
图1. 1984~2019年第一产业从业人数
索罗–斯旺模型中对于经济增长中含有技术进步的影响,主要表现在从业人员对经济增长影响中存在乘数效应,而资本存量对于经济增长的影响则仅仅为简单的加法效应 [9] 。另外对于从业人员的出生率角度分析,结果见图2,自1978年改革以来我国实行计划生育政策,我国各地区农村新增人口出生率大幅下降,也在一定程度上跳出索罗–斯旺模型经济增长的虚假繁荣陷阱,并随着技术因素与资本存量对于经济增长的影响,呈现长期稳定的因素。
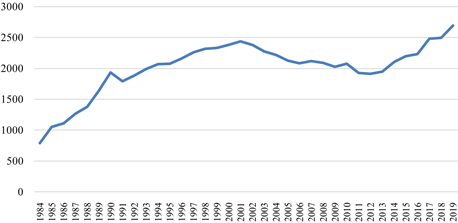
Figure 2. Capital stock in rural areas, 1984 to 2019
图2. 1984~2019年农村地区资本存量
从当前我国农村地区资本存量整体情况来看,我国农村地区资本存量整体呈现上升趋势,而在2001年~2012年间存在一定程度的下降,且在当前阶段来看,仍存在很强的上升势头 [10] 。这说明目前我国农村地区具备一定程度的发展基础与发展潜力。但同时也暴露出一些问题,例如资本如何使用与资本使用效率等问题,这需要在后续的研究中逐渐解决。
而我国农村地区当前资本量正呈现逐渐积聚现象,一方面伴随着农村地区二、三产业的发展,使得农村地区经济发展趋于多样化,为其第一产业农业发展积累资金,另外一方面国家鼓励农村青壮年劳动力就地创业、返乡创业,并给予其政策支持,使得农村地区青壮年劳动力返乡发展,为农业发展奠定基础。而农村地区农业发展,伴随着中国工业化发展进程逐步加快,工业部门逐步成为社会经济发展的主导部门 [11] ,特别是在我国广大中西部的农村地区,农业部门的主导型逐渐被工业部门所取代。但由于农业部门作为社会经济发展的基础,其基础性与生存保障性功能,并未被其他产业部门所取代。
我国当前处在经济发展过程中工业化中后期阶段,存在一定工业反哺农业、城市带动乡村的一般发展规律 [12] 。党的十六届四中全会明确指出:“农业是安天下、稳民心的战略产业,必须始终抓紧抓好。纵观一些工业化国家发展的历程,在工业化初始阶段,农业支持工业、为工业提供积累是带有普遍性的趋向;但在工业化达到相当程度以后,工业反哺农业、城市支持农村,实现工业与农业、城市与农村协调发展,也是带有普遍性的趋向。” [13]
而我国农业地区资本量的积累很大程度上归功于工业部门的发展,这使得农村地区发展跳出传统的“二元经济”结构,朝着城市与农村、工业与农业协调健康发展。
另外索罗–斯旺模型中对于影响资本存量大小的变动假设的在于银行存贷款利率的大小变动,认为投资者均是理性人,对于其经济行为的假设过于理想化。1911年,货币主义学派代表人物美国经济学家欧文费雪在其《货币的购买力》一书中提出著名的“费雪交易方程”,即假设流通速度不变的情况下,投资者对于货币的需求量取决于投资品价格与产品数量,强调货币作为交易媒介即流通手段的作用;而后货币主义学派代表人物弗里德曼在吸收和修整凯恩斯灵活偏好论的基础上,推演出新货币数量论,即认为投资者对于货币需求不仅取决于产品价格与产品数量,更取决于金融市场的存贷款利率、M1和M2的比率与预期物质资产收益率等 [14] 。
但在实际研究中我们发现,由于调查研究对象为我国广大的农村地区,且大多分布在我国的中西部地区,较东部发达地区而言,我国中西部地区金融市场不发达、未形成理性的投资环境,且国家政策与大型投资机构在中西部农村地区中的作用较大,个体投资者对于其个人决策上较为保守。因此使得我国中西部的广大农村地区在上述西方经济理论影响分析中影响路径与影响因素并不显著,但我们在后文的模型构建上,仍可以借鉴西方经济理论中的可取之处。
3. 模型设定、数据来源与研究方法
3.1. 模型引出
由于在中国农村,可利用可观测的样本观测值有限,且可利用到的数据有限,这使得索罗–斯旺模型的应用成为必要,因为索罗–斯旺模型只考虑到我们所关心的基本内容 [15] 。这里首先引入经济增长率的概念:即从抽象的意义上讲,设变量Z(t)是时间变量t的市值函数,则变量Z从时间t到时间
的增长率被定义为如下关系式:
如果让时间改变量
,则在变量Z(t)关于时间的增长率关系式为:
此时由于经济增长的概念是清晰的,但导致经济增长的原因却是复杂的,本文借助索罗–斯旺模型,目的是减少经济增长的影响因素,将解释变量限制在资本与劳动力,并将模型建立在一个新古典生产方程体系上,引入增长核算这种经济分析方法,将观测到的总产出增长分为几个部分,而各个部分与各要素的投入变化与生产技术的变化相关:
其中A为全要素生产率,K为资本量,N为人口资本量。借着上述关于增长率理论,可将其表述为
即:产出增长 = 生产率增长贡献 + 资本增长贡献 + 劳动增长贡献,而全要素生产率无法直接观测与搜集,因此通过间接衡量进行观测:
根据索罗–斯旺模型前提假设:(1) 经济由一个部门组成生产一种即可投资又可消费的商品。(2) 不存在国际贸易的封闭经济,且政府部门被忽略。(3) 生产的规模报酬不变。(4) 经济技术、人口增长与资本折旧速度外生。
由于未能从国家统计局、中国统计年鉴等数据库中找到农村地区资本总量数据,根据(2)假设,且根据凯恩斯学派有关两部门模型均衡理论,定义资本为可支配收入在进行消费后的结余,可得
,即人均资本 = 农村居民可支配收入 − 农村居民人均消费支出。另外这里的总产值为农林牧副渔业总产值,即第一产业总产值,忽略农村从业人员从事第二、三产业的产出贡献,且这里人力资本使用第一产业从业人员人数进行衡量 [16] 。
注:数据来源于中国统计年鉴。
根据表1数据,以上一年数据为基础,进行增长率计算,可得:全要素生产率是作为一个余量进行计算得出,即为考虑了可直接导致产出增长,结果见表2。
注:数据来源于上述数据整理计算。
根据全要素生产率的定义可知,全要素生产率是作为余量计算的影响解释因素,即不能被投入要素解释的部分,一般被认为是由于技术因素的变动引起的产出增长。这里我们导出全要素生产率按年份变化的折线图,结果如图3所示。
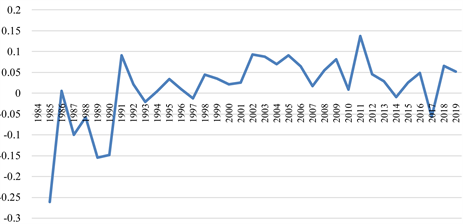
Figure 3. Total factor productivity in 1984~2019
图3. 1984~2019年全要素生产率
可以看到在最初1991年之前,技术水平导致产出增长呈现出负增长率,这可能是因为资本与人力资源对产出增长的贡献相对于全要素增长率来讲贡献较大。而在1991年至2019年中,全要素生产率呈现正增长,虽各年存在波动,但整体围绕某一值上下波动。根据图示信息,猜测这里全要素生产率时间序列可能为平稳序列,以下对其全要素生产率这一时间序列进行单位根检验。
注:**表示在1%的显著水平上拒绝有单位根的原假设。
从表3中可以看出,在选择滞后阶数时,采用系统推荐滞后阶数。而在单位根检验中,全要素生产率的ADC检验值为−5.388406 < −3.639407,在1%的显著水平下拒绝其有单位根的原假设,认为其不存在单位根,即全要素生产率增长率为平稳序列。这说明,全要素生产率对于农村地区经济增长的影响中,呈现一种不确定的趋势与波动性,但从数据来看,全要素生产率波动围绕均值1.25%上下波动,且方差为0.0063,这说明从整体来看,全要素生产率不随时间变动,但每年均存在一定程度上由于技术水平提升所导致的农村地区经济增长影响。
3.2. 模型说明
在研究总生产函数的传统分析框架中,由于技术因素是由衡量增长的决定因素计算后的剩余余量得出的,且从实际度量上并未找到相关替代数据对其进行衡量 [17] 。因此在实际计量模型构建中,可将全要素增长率作为资本与劳动人口对产出影响进行全微分后进行模型回归时的截距项进行研究分析,而在考虑实际产出影响模型时,可以得出索罗–斯旺模型中反映资本与劳动人口对经济产出的生产函数:
这里Y表示第一产业经济产出,K表示农村地区总的资本投入,L表示第一产业劳动力投入。对其产出模型进行全微分,可得到以下等式:
在上式中,资本与劳动人口对产出的贡献率存在一定共性,即资本与人口两者作为产出衡量的解释变量,不仅反映出各时期内的产出贡献程度,又体现出一定量的资本与劳动人口发展水平。但考虑到收入分配结构、收入分配制度和政府政策行为等因素在地区间存在差异,即对其各地区产出影响不同。这里并将国家统计局与中国统计年鉴的相关数据进行地区分类,且由于研究对象是农村地区的可持续发展,因此取第一产业人均产出替代第一产业总产出,使用农村地区人均资本投入量替代农村地区总的资本投入,用β1来表示资本对产出贡献,用β2表示劳动人口对产出贡献,μ作为截距项表示全要素增长率,即反应技术因素对第一产业发展的影响。从而建立产出增长模型:
数据说明本文涉及到的变量与数据资料主要包括第一产业人均产出、农村地区人均资本和第一产业从业人口三个方面,我们选择1984~2019年的农村地区数据进行分析研究。由于数据较大,我们对第一产业人均产出、农村地区人均资本和第一产业从业人口取对数,为的是减少数据的波动与回归系数大小的处理。
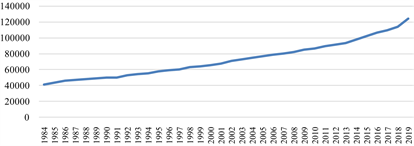
Figure 4. Change curve of output value of primary industry
图4. 第一产业产值变化曲线
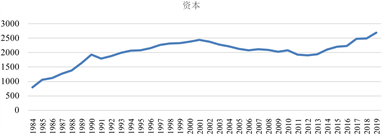
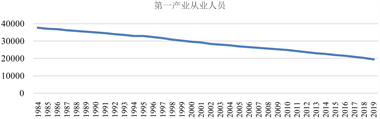
Figure 5. Overall trends in capital per capita and working population
图5. 人均资本和从业人口整体趋势
图4描述了我国第一产业产值变化,图5描述了我国农村资本和第一产业人口变化趋势,可以看出:随着时间的变动,我国第一产业人口呈现逐年下降的趋势,而在产出与资本上,则呈现总体上升趋势。并且在实际分析中,由于其存在明显的趋势项且存在截距项,因此我们在后面的实证分析中,可能其数据并非平稳,但数据间可能存在协整关系。因此我们将对这三组数据进行处理,通过对其单位根检验,对其数据平稳性进行研究,分析是否为平稳的AR模型,而后再进行协整检验,建立平稳的ARMA模型,并通过格兰杰因果检验,观测变量间的格兰杰关系,最后通过误差修整模型,分析确定模型。本研究所涉及的数据来源于《中国统计年鉴》(1984到2019年历年)、国家统计局(1984~2019)。
3.3. 实证分析方法
为了避免模型出现伪回归的现象,在进行时间序列数据处理上,首先将利用Dickey和Fuller (1981)提出的考虑残差项序列相关的ADF单位根检验法,检验变量的平稳性,对于非平稳性的变量进行处理使之成为平稳时间序列。如果变量是单整的,那么我们将对相关变量进行协整检验(Cointegration Test)分别确定第一产业从业人员和农村人均资本量与第一产业人均产出之间是否存在长期协整关系。
协整理论是研究分析非平稳时间序列的一个重要方法。Engle and Granger (1987)指出,如果两个或两个以上的非平稳时间序列(含有单位根的时间序列)的线性组合能构成平稳的时间序列,则称这些非平稳时间序列是协整的,称得到的平稳的线性组合为协整方程,可以认为协整方程的存在说明这些变量(即非平稳的时间序列)之间存在长期的均衡关系。协整理论是研究分析非平稳时间序列的一个重要方法。
4. 实证检验结果与分析
4.1. 单位根检验
本研究利用Eviews软件,考虑使用残差项序列相关的ADF单位根检验法,对各变量进行单位根检验,以确定变量的平稳性 [18] 。首先对农村地区第一产业从业人数、人均资本量、第一产业人均产出取对数,以减少数据的波动,分别用LNN、LNK、LNY表示。根据ADF单位根检验发现,LNN、LNK、LNY三者均为非平稳变量,于是我们对于非平稳变量处理采用差分法。结果见表4其中△LNN、△LNK、△LNY分别表示对其相关变量取一阶差分值。从表1可以看出,经过一阶差分处理后所有时间序列数据在1%显著水平下都是平稳的。
注:**表示在1%的显著水平上拒绝有单位根的原假设。
4.2. 协整检验
由于上述变量都是单整的,因此,我们可以利用Johansen协整检验判断它们之间是否存在协整关系,并进一步确定相关变量之间的符号关系。由单位根检验我们可以知道,DLNY、DLNK、DLNK三者时间序列均含有线性趋势项和常数项,相应地协整方程也应该包含趋势项和常数项项(Johansen,1994;赵华、潘长凤,2004)。而Johansen协整检验是一种基于向量自回归模型的检验方法,在检验之前,必须首先确定VAR模型的结构。根据SC准则可以确定DLNN、LDNK、DLNY模型的最优滞后期数为0;同时,我们利用Q统计量检验、怀特检验和JB检验进一步检验滞后期数为0的VAR模型,发现其拟合优度很好,残差序列具有平稳性,的确是最优模型。在此基础上,我们可以进行协整检验,结果如表5所示。

Table 5. Results of co-integration test of rural capital, employment and output (sample interval: 1984~2019)
表5. 农村资本和从业人数与产出的协整检验结果(样本区间:1984~2019)
注:**表示在1%的显著水平上拒绝有单位根的原假设。
协整检验在1984~2019年的样本区间中,协整关系十分明确,即DLNY、LDNN、DLNK三个变量之间存在协整关系,可据此建立误差修正模型,可以得到误差修正模型:
则LNY、DNK、LNN三个变量之间的协整方程是:
这表明了在1984~2019年中,三个变量间LNN与LNY存在一个长期均衡关系,但LNK与LNY之间的长期均衡关系并不显著。从中可以发现1984~2019年间,农村地区第一产业人均产出与第一产业从业人数间存在一个反向关系,而农村地区第一产业人均产出和农村地区人均资本量间存在正向关系,但整体上农村地区第一产业产值呈现上升趋势。
这说明在1984~2019年间,第一产业从业人员整体上呈下降趋势,人均资本量呈现上升趋势,总体来说,经济增长中包含技术因素,且技术的增长对人均产出呈现促进影响 [19] ,而在上述分析中,全要素增长率的变动呈现波动,且整体平稳,因此在理论分析时可以省去其技术增长的影响,且在对农村地区第一产业人均产出、第一产业从业人数和农村地区人均资本量的协整检验中,发现其可能存在长期均衡关系。
但在LNY、LNK、LNN三个变量间确定长期均衡关系后,我们又通过误差修整模型确定其变量之间的短期动态关系,可以发现LNK对LNY的变动系数并不明显,这说明在经济发展中短期人均资本存在对于第一产业人均产出影响并不明显,但在LNN对LNY的变动中,可以看到其对第一产业的人均产出影响较大,数据表明伴随着第一产业从业人数的降低,第一产业人均产量变动反应较大,这在理论分析上可以说明在1984~2019年间,全要素增长率中技术等因素的增长对第一产业发展贡献较大。
4.3. 格兰杰因果检验
在上述分析中,尽管LNN、LNK对LNY这三者变量间存在长期关系,但LNK与LNY的长期均衡关系并不显著,因此我们需要进一步利用格兰杰因果检验对其变量间关系予以分析,其最优滞后项选择根据AIC、SC和HQ准则进行检验,结果如表6所示:

Table 6. Variable lag order selection test
表6. 变量滞后阶数选择检验
注:*表示在该标准下所选取的滞后项数。
根据AIC、SC和HQ准则,我们可以选择0阶最优滞后项进行格兰杰因果检验,表7检验的是∆LNN和∆LNK同∆LNY的格兰杰因果检验关系,从表6可以得知,在取得最优滞后期0阶以后,∆LNN与∆LNY的Granger因果检验结果表明,在5%的置信度下,拒绝“∆LNN不是△LNY的Granger原因”的原假设,认为∆LNN是∆LNY的Granger原因。然而另一方面,在10%的置信度下,△LNK没有成为∆LNY的格兰杰原因。

Table 7. Granger causality test (sample interval: 1984~2019)
表7. Granger因果检验(样本区间:1984~2019)
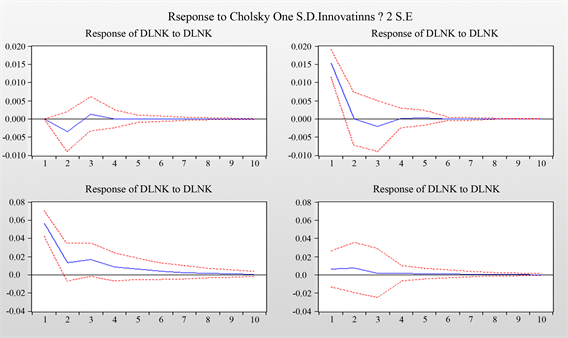
Figure 6. Dynamic response of per capita capital stock in rural areas and per capita output growth of primary industry in rural areas to related shocks
图6. 农村地区人均资本存量与农村地区第一产业人均产出增长对相关冲击的动态反应
然而根据索罗–斯旺模型理论分析上,在资本、劳动力同产出的关系上,中国农村地区第一产业人均产出与农村地区人均资本量和第一产业从业人数上存在某种程度上的联系 [20] ,但可能由于中国当前农村地区经济发展程度较弱,使得资本对农村地区产出贡献较低,这可能是导致在Granger因果检验中,在10%的置信度下,没有拒绝“∆LNK不是∆LNY的Granger原因”的原假设,
由于格兰杰因果检验无法证实农村地区人均资本存量是农村地区第一产业人均产出增长的原因,因此我们需要利用向量自回归模型(VAR)进行冲击反应分析(Impulse-Response),以进一步细化探索变量之间的关系。图6是农村地区人均资本存量与农村地区第一产业人均产出增长对相关冲击的动态反应。
从图6中可以看出:(1) 农村地区人均资本存量的负向自冲击会呈现自身的优化;(2) 农村人均资本存量的变动对农村第一产业人均产出导致其产生同向变动,而在滞后2期达到最大的正向效应,从滞后3期以后,这种冲击效应得以改善。这说明在农村地区人均资本存量与农村地区第一产业人均产出增长的向量自回归模型中(VAR),二者存在一定量的滞后相关关系。这也证实了索罗–斯旺模型在理论上对农村地区人均资本存量与农村地区第一产业人均产出增长两者关系的研究 [21] 。
5. 结论及政策建议
实证结果清楚地显示:我国农村地区1984~2019年间,农村地区经济的发展,无论是在理论分析还是实证分析结果上,资本存量的增长会带来农村地区经济的发展,且由于存在技术增长等外在因素的影响,使得第一产业从业人员数量的下降也会使得农村地区产出的增加。但在我国农村地区经济发展中,由于各地区发展存在一定差异,使得劳动人口作为人力资本因素在地区间流动,这导致索罗–斯旺模型中原本起重要作用的人口增长因素,变得微乎其微,从而使得农村地区的劳动人口未能成为农村地区产出增长与经济发展的重要影响因素,但在实际实证分析中,由于全要素生产率的存在,使得农村地区劳动人口的流失并未成为阻碍农村地区发展的因素,也并未成为直接导致城乡经济发展差距拉大以及“二元结构”的强化。这一结果论证得出在我国农村地区经济发展过程中,农村地区资本存量与劳动人口实则是“鱼和熊掌”的关系,肯定了经济增长中资本对于经济增长之间的正向关系适用于我国农村地区长期均衡增长理论有效性,同时也证明了农村地区技术增长真实存在,且在现行农村地区经济发展战略与当前农村土地流转制度的背景下,我国农村地区资本存量变动与农村地区产出增长变动相互协调的事实。
在我国广大中西部农村地区,第一产业的产出作为衡量地区农业可持续发展的重要衡量指标与农村地区经济发展的重要目标,其在当前我国目前已全面进入小康社会阶段,过去农村地区仅靠劳动人数来增加农业产出总量增长的时代已经过去,而农村地区资本存量的积累与技术因素的提升对于农村地区农业产出增长之间的正向作用关系,不仅是在理论逻辑和实证分析上存在和行得通的,并且对于当前我国农村地区农业可持续发展,稳定经济结构,保证社会稳定等方面也是必须的。
在中国,广大农村地区实现农村地区可持续发展这一重要目标是不应动摇的,然而为实现农村地区可持续发展这一目标,宏观指导、制度安排与微观分析对于解决上文所提到的问题而言都是至关重要的。一方面针对我国广大农村地区自然环境的差异导致的污染问题,应及时建立农村户级责任制,针对由于技术、专业知识等原因导致的问题,将责任落实到人,并针对当前已存在的环境问题有针对性的开展治理;另一方面针对我国中西部各地区农村农业产业化水平较低问题,加强基础设施建设,加强地区间的生产协作,破除原本按乡镇的土地划分界限,并逐步提高农村地区现代化、规模化与集约化农业发展;另外针对当前城乡农产品销售问题上,建立横纵交错的销售网络,并提高信息开放水平,避免城乡双方信息不对称现象,并依托网络平台,扩展农产品销售渠道,树立农业农产品品牌效应,避免过去销售网络与销售半径存在的短板。最后针对农业资本如何使用与资本使用效率较低等问题,由于实证分析中资本对于经济发展的贡献较低,必须提高资本的使用效率,具体分析各地区工业发展阶段水平,并确定不同农业项目的投资比例,依据农村户级责任制,具体到户责任到人进行资本投资指导,对原先资本投资效率较低的生产环节进行调整,并调节各环节投资比重,使农村地区农业生产与工业生产二者均衡发展,实现农村地区可持续发展,并逐渐破除“二元结构”,减小城乡差距。