HXD3型机车车轮磨耗数据建模与镟修策略优化

Modeling of Wheel Wear Data and Optimization of Re-Profiling Strategy for HXD3 Locomotives

摘要: 机车车轮的磨耗难以避免，研究车轮磨耗规律，优化镟修策略具有重要意义。本文首先介绍了车轮常见的损伤种类和镟修机理，后建立了轮缘厚度磨耗模型、轮径磨耗模型和基于上述模型利用蒙特卡洛方法提出的一种车轮镟修策略优化方案，以降低车轮全寿命周期的使用成本。在建立磨耗模型过程中，分别采用二次曲线拟合轮缘厚度磨耗速率模型和高斯分布拟合轮径磨耗模型；对136组镟修策略的仿真结果表明，车轮轮缘厚度在28~32.5 mm时车轮的生命周期较长，其中镟修前后轮缘厚度为28.5 mm，31.5 mm时为最优镟修策略，此时车轮仿真预期使用寿命最长、车轮平均使用成本最低。

Abstract: Wear of locomotive wheels is unavoidable, and it is of great significance to study the wheel wear pattern and optimize the re-profiling strategy. This paper firstly introduces the common types of wheel damage and re-profiling mechanism, and then establishes a wheel flange thickness wear model, a wheel diameter wear model and a wheel re-profiling strategy optimization scheme based on the above models using the Monte Carlo method, so as to reduce the cost of wheel life cycle. In the process of establishing the abrasion model, the quadratic curve is used to fit the flange thickness wear rate model and the Gaussian distribution is used to fit the wheel diameter abrasion model, respectively; the simulation results of 136 groups of re-profiling strategies show that, when the thickness of wheel flange before and after re-profiling is 28.5 mm and 31.5 mm, the wheel life cycle is the longest of 75 months, which corresponds to the lowest average cost of 880 yuan/month.

1. 引言

随着车辆运行，车轮与钢轨的不断接触必然造成车轮踏面的磨耗甚至损伤 [1] 。因此当车辆运行一段时间后，需要对车轮进行镟修，恢复到正常运行的廓形。如何预测车轮磨耗状态并对车轮镟修方案进行优化已然成为铁路相关研究的主要方向。然而，预测车轮磨损是一项复杂和具有挑战性的任务，主要归因于各种复杂的复杂性。这些复杂的问题包括车辆轨道动力学的模拟、轮轨滚动接触的建模、磨损率的确定和其他技术细节，如每个周期后的轮廓的平滑和更新 [2] 。许多学者对这些问题进行了研究。目前，对车轮磨耗和镟修的研究主要分为两个方面，其一是从车辆动力学和轮轨接触关系结合磨耗模型正向推导出车轮磨耗规律，从而给出镟修建议 [3] [4] [5] ，结合轮轨匹配分析和车轮磨损模拟，揭示影响轮缘严重磨损的关键因素 [6] 。其二是从轮对历史磨耗数据进行数据建模，进行车轮廓形尺寸预测及更新 [7] [8] [9] [10] ，并采用蒙特卡洛仿真等方法，得不同镟修策略的实际经济效果 [11] 。其中基于车辆动力学的磨耗研究已较为成熟，而基于历史检修数据的信息挖掘与建模正随着数据分析方式的更新展现出强大的生命力。本文从车轮常见损伤和镟修机理出发，基于大连机车车辆有限公司四年间的HXD3型电力机车车轮检修数据库，建立轮径、轮缘磨耗模型研究车轮磨耗规律，并优化车轮镟修策略以获得更低的车轮使用成本。

2. 理论基础

2.1. 车轮常见损伤种类及原因

机车车轮常见的损伤种类主要有以下三种。

1) 轮缘及踏面磨耗。在车辆运行过程中，踏面与钢轨之间的摩擦会导致踏面圆周磨耗，而当车辆经过曲线线路时，离心力使得车轮轮缘与钢轨发生挤压摩擦，轮缘会因此变薄甚至产生裂纹。磨耗达到一定程度时则需要进行镟修，使车轮恢复到标准廓形。实际上，轮缘及踏面的磨耗是车辆运行过程中不可避免的。

2) 踏面擦伤和剥离。踏面擦伤一般是由于车辆在制动过程中，车轮抱死发生滑行，从而导致圆形踏面产生平面疤痕，严重影响列车的行车安全。踏面剥离指的是车轮踏面在解除疲劳和制动热的作用下，踏面圆周产生金属掉块剥落的现象，其危害与踏面擦伤类似。

3) 车轮多边形。车轮多边形指车轮发生磨耗后出现的非圆现象。出现车轮多边形的成因较为复杂，轮对结构共振是车轮多边形磨耗形成的内在因素，不合理的车轮镟修对车轮多边形磨耗的形成和发展起到至关重要的作用 [12] 。

图1给出了几种常见的车轮失效形式示意图或者实物图。

(a) 车轮磨耗(b) 车轮擦伤(c) 高阶车轮多边形 [12]

Figure 1. Common forms of wheel failure

图1. 车轮常见失效形式

当车轮出现以上失效情况时，需要通过镟修使得车轮外形尺寸参数在标准运行范围内。

2.2. 车轮镟修机理

不考虑因车轮擦伤等异常损伤而进行的镟修，车轮的主要失效参数是轮缘和踏面磨耗，轮对在正常运行情况下，轮缘厚度的磨耗一般比轮径磨耗快。当轮缘厚度小到一定范围内，车辆通过曲线时轮缘顶点易于爬上尖轨从而导致列车车辆脱轨 [13] 。并且在目前的镟修策略中，都是以牺牲轮对直径为条件，达到恢复轮缘厚度的目的同时必须保证镟修后的车轮外形尺寸参数在标准运行范围内。图2为轮对镟修和更换时轮径和轮缘厚度的状态示意图，其中Sd为轮缘厚度，D为轮径值，Sdh为镟修上限，Sdl为镟修下限。当车轮轮缘厚度磨耗至轮缘厚度下限以下时，进行一次镟修，将轮缘厚度恢复至轮缘厚度上限。镟修比例系数k被定义为镟修前后车轮直径的减小量与轮缘厚度增大量之间的比率。HXD3型机车车轮踏面廓形为JM3磨耗型踏面，k值取4.2。

3. 车轮磨耗建模

3.1. 轮缘厚度磨耗模型

为了研究轮缘厚度磨耗规律与车轮使用寿命周期的关系，通过公式(1)计算出每月的轮缘厚度磨耗量作为轮缘厚度磨耗模型的输出变量：

$V_{Sdi}=\frac{S{d}_{i+1}-S{d}_i}{t_{i+1}-t_i}\times 30$ (1)

式中， $t_{i+1}$ 和 $t_i$ 表示测量出该轮缘厚度数据的日期， $S{d}_{i+1}$ 和 $S{d}_i$ 分别为不包含镟轮情况下 $t_{i+1}$ 和 $t_i$ 日期的轮缘厚度测量值。

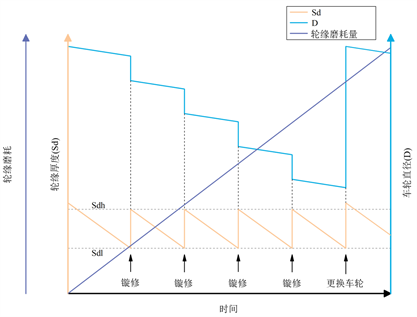
Figure 2. Wheel re-profiling and replacement schematics

图2. 车轮镟修和更换示意图

通过对比，选取大连机车车辆有限公司2018~2021四年间积累形成的HXD3型电力机车车轮检修数据库中服役周期最久、运行里程最长的10辆机车的轮缘厚度数据作为建模样本，并去除样本数据中的毛刺数据，绘制轮缘厚度散点图分布如图3所示。

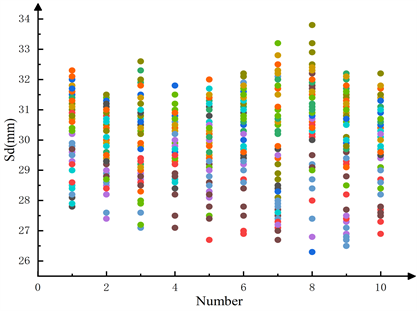
Figure 3. Flange thickness distribution

图3. 轮缘厚度分布散点图

共提取数据库轮缘厚度值1056条，经式(1)计算得到885条轮缘厚度磨耗速率值，将同一轮缘厚度下的轮缘厚度磨耗速率取均值，最后将轮缘厚度和轮缘厚度磨耗速率的计算数据进行拟合，结果如图4所示。

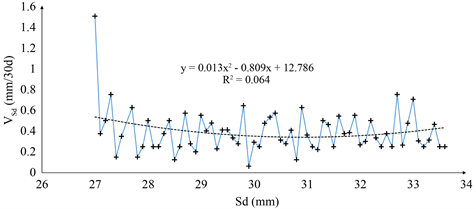
Figure 4. Fitted curve for flange thickness and flange wear rate

图4. 轮缘厚度和轮缘磨耗速率拟合曲线

选用二次曲线拟合轮缘厚度磨耗速率与轮缘厚度的关系，方程表达式为：

$V_{Sd}=0.013S{d}^2-0.809Sd+12.786+R{V}_{Sd}$ (2)

式中 $R{V}_{Sd}$ ~N(0, 0.226)，为样本值与预测值之间的误差函数，其中0.226为极大似然估计得到的标准差。

3.2. 轮径磨耗模型

经计算，轮径磨耗速率与检修数据中的轮径值、轮缘厚度等均无明显相关性，因此考虑采用分布律进行拟合建模。提取数据库中的所有1号车轮的轮径磨耗量，得出每四个月轮径的磨耗量基本分布在0~5 mm之间，因此将[0, 5]以0.1间距分为五十个小区间，统计各个区间内的轮径磨耗量的频数，得出如图5所示的频方图。

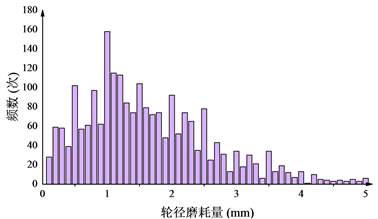
Figure 5. Frequency histogram of wheel diameter wear distribution

图5. 轮径磨耗量分布频方图

从图5可以看出，轮径磨耗量近似服从正态分布，因此采用正态分布函数对该轮径磨耗量进行高斯分布拟合，如图6所示，正态分布的概率密度函数如式(3)所示。

$f\left(x\right)=\frac{1}{\sqrt{2\text{π}}\sigma }{\text{e}}^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}$ (3)

其中 $\mu =1.634,\sigma =0.984$ 。

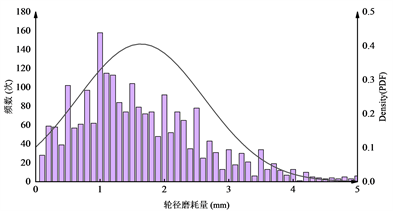
Figure 6. Fitted graph of wheel diameter wear distribution

图6. 轮径磨耗量分布频方图

4. 镟修策略优化

根据轮缘厚度统计数据，大多分布在26~34 mm之间，同时为避免出现上限太低的无意义镟修方案，以0.5 mm为间隔确定Sdl和Sdh，对应得到136种镟修策略，仿真流程如图7所示。

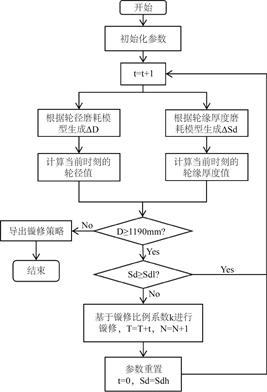
Figure 7. Re-profiling strategy simulation flow

图7. 镟修策略仿真流程

如图8所示，图8(a)~(c)为136种镟修策略分别对应的镟修上下限，镟修次数和使用寿命。从图8(a)、图8(b)中可以看出，当镟修方案的镟修下限一定时，镟修上限越低，对应镟修次数越高，这在轮对的全寿命周期中会因镟修次数过多影响有效服役时间，同时且浪费大量财力物力。从图8(b)、图8(c)中可以看出，仿真出的镟修次数多分布在5~10次，车轮的预期生命周期多分布在55~65个月。在136种镟修策略中，预期生命周期最长为75个月，约为6.3年，对应镟修上下限为[28.5, 31.5]，镟修次数为6次。将所有镟修策略中预期生命周期不低于70个月的策略汇总，见表1。从表1可以看出镟修上下限在28~32.5 mm时车轮的生命周期较长，这表明此时的车轮踏面与钢轨磨合达到相对平稳的状态，轮缘与轨道之间的摩擦较少，当镟修后轮缘厚度仍处在此区间时，车轮预期使用寿命相对较长。

Figure 8. Simulation results

图8. 仿真结果

最后，以更长的生命周期和最低的镟修次数为原则，考虑单轮更换成本和单轮镟修成本，计算出单轮平均使用成本最低的最佳镟修策略。目前，HXD3型车轮单轮更换成本为60000元，单次镟修成本为1000元，以64号镟修策略为例，其预期单轮平均使用成本为(60000 + 1000*8)/70 ≈ 971.43元/月。由表1可得，在综合考虑镟修次数和生命周期以及平均使用成本的情况下，通过计算和对比，镟修上下限为(28.5, 31.5)的76号策略为最佳镟修策略，其预期使用寿命可以达到6.3年，平均使用成本最低，为880元/月。

Table 1. The preferred re-profiling strategies

表1. 较优镟修策略

5. 结论

本文基于HXD3型机车车轮磨耗数据，建立轮缘厚度磨耗模型和轮径磨耗模型，然后利用蒙特卡洛方法仿真136种不同镟修前后轮缘厚度下的车轮全寿命周期磨耗情况，对比得到最优镟修策略。结果表明，车轮轮缘厚度在28~32.5 mm时车轮的生命周期较长，其中镟修前后轮缘厚度为28.5 mm，31.5 mm时为最佳镟修策略，此时车轮仿真预期使用寿命最长、车轮平均使用成本最低。相比以往的镟修方式，车轮寿命提高的同时兼具了更低的使用成本，为车轮数据挖掘使用和工人镟修提供参考。

此外，本文中仅对检修数据库中部分数据进行了调用，轮缘高度、轮缘角和轮径差等相关数据仍未得到使用，随着测量、计算技术的发展，充分挖掘车轮检修数据信息对实现车轮运维智能化管理有重要意义。

基金项目

辽宁省教育厅科学研究项目(LJKZ0493)；大连市科技创新基金应用基础研究项目(2022JJ12GX029)。