1. 引言
弧齿锥齿轮是在重要的动力传动系统中传递动力和运动的一种较为复杂的齿轮。该传动过程具有重合度大、传动平稳、承载能力高、噪声低的优点,适用于高速齿轮传动。然而,锥齿轮传动过程中产生应力集中和轴向力会影响齿轮和轴承寿命 [1] [2] [3] 。
田志勇 [4] 分析了齿向修形方式,探究了斜齿轮齿向修形的曲线优化。蒋进科 [5] 根据人字齿轮传动的特点,提出小轮轴向浮动安装的齿面修形优化设计方法,将修形曲面与理论齿面叠加构造修形齿面。对于锥齿轮适当的齿向修形对改善齿轮啮合情况和轴向力有着十分重要的影响。姚贵金 [6] 分析了轴向力对弧齿锥齿轮使用寿命的影响,提出了通过合理安排轴向力来提高锥齿轮使用寿命的措施。王明松 [7] 对弧齿锥齿轮的旋转组合进行了优化,可以避免轴向力的叠加,从而提高了减速器齿轮轴和箱体的压力,提高了齿轮和轴承的寿命。Wu Y等 [8] 为双弧斜齿轮液压泵工作过程中产生的轴向力提供了一种新的分析思路和平衡方案,可以减少轴向力引起的端部间隙泄漏,提高齿轮液压泵的容积效率。刘卫等 [9] 分析两个齿轮中间轴的螺旋方向往往是相同的,因此其轴向力可以部分抵消。这将减少滚动轴承、杆和齿轮箱的轴向负荷,并延长其使用寿命。为同类齿轮的设计和安装提供参考。朱美琳等 [10] 提出了一种可调节的轴向推力结构来抵消齿轮的轴向力。
针对减小锥齿轮轴向力,改善啮合情况,本文提出弧齿锥齿轮齿向采用抛物线齿向形式达到抵消部分轴向力的目的,从而减小锥齿轮的轴向合力,提高齿轮轴端轴承寿命。利用UG二次开发实现抛物线齿形球面渐开线锥齿轮的快速建模,分析在不同抛物线焦准距下,抛物线齿形对锥齿轮的轴向力影响。
2. 抛物线锥齿轮数字化建模
2.1. UG二次开发简介
UG是目前市场上集CAD/CAM/CAE于一体的主流三维设计软件,通过强大的三维设计能力,能够轻易的构建各种复杂结构的三维模型。同时还具备参数化、特征化的设计理念。UG提供了许多可用的库工具和二次开发工具来为用户构建部件。吴家洲等 [11] 介绍了UG二次开发的各种模块和用法。UG不仅具有强大的实体造型、曲面造型、虚拟装配和工程图设计等功能,还提供了Grip和API程序设计模块以及两个辅助开发模块,同时还具有良好的高级语言接口。在这些二次开发模块的辅助下,UG的参数化能力变得更为强大。
传统的齿轮建模方法是按照机械手册计算齿轮设计参数,手动完成建模。从轮坯到整个模型的生成都需要手动生成,相较于数字化建模,传统建模方法无论在精度或者速度上都无法与之相比。UG二次开发的齿轮数字化建模,是基于齿廓生成原理,利用程序使得从齿面点生成到齿轮实体建模整个过程完全自动化。
2.2. 齿轮数字化建模过程
2.2.1. 齿廓曲线构建
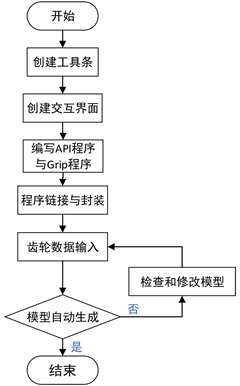
Figure 1. UG/OPEN development process
图1. UG/OPEN开发流程图
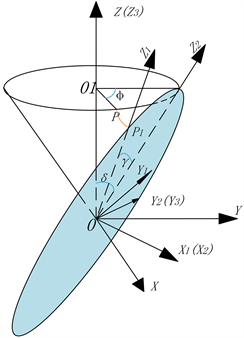
Figure 2. Generation principle of spherical involute
图2. 球面渐开线的生成原理
理论上来说,利用球面渐开线的形成原理得到的齿面是完全共轭的。由于齿轮的制造、安装的误差,以及轮齿啮合对数、啮合点位置和瞬时传动比不断变化,使得齿轮刚度不断变化。因此一般采用局部共轭原理进行加工。将球面渐开线的齿廓在背锥上投影展开,即以直代曲的近似分析和设计方法。这种近似方法必然会影响弧齿锥齿轮的设计精度,在一定程度上影响了弧齿锥齿轮的特有优点,降低了其使用性能。随着数控加工技术的不断发展,点位式加工方法越来越成熟。本文在点位式加工方法的基础上利用球面渐开线生成原理,结合UG二次开发构建抛物线齿形球面渐开线锥齿轮。二次开发流程如图1所示。
球面渐开线是一条空间曲线,使用显示方程推导的难度较大,本文将P点所在的动坐标系经过齐次坐标变换与基圆锥坐标系统一,以此获得球面渐开线上一点的方程。随着
角变换得到一条连续的球面渐开线。球面渐开线的生成原理如图2所示。
下面对P点所在动坐标系变换到基圆锥坐标系的过程进行说明:在坐标系OX1Y1Z1中,Z1轴通过P`点,X1垂直于平面O向下。坐标系OX1Y1Z1绕X1顺时针旋转
角形成OX2Y2Z2。将坐标系OX2Y2Z2绕Y2顺时针旋转
角形成OX3Y3Z3。最后将坐标系OX3Y3Z3绕Z3顺时针旋转
角变换到OXYZ坐标系。
其中坐标系OX1Y1Z1绕X1顺时针旋转
角形成OX2Y2Z2的变换矩阵为:
(1)
坐标系OX2Y2Z2绕Y2顺时针旋转
角形成OX3Y3Z3的变换矩阵为:
(2)
坐标系OX3Y3Z3绕Z3顺时针旋转
角形成OXYZ的变换矩阵为:
(3)
综上所述,坐标系OX1Y1Z1到OXYZ的坐标系变换矩阵:
(4)
即:
(5)
以上式中Rb为动坐标系z轴的长度,它对应基圆锥的母线,随着Rb的变化可得到不同母线位置的球面渐开线。
为球面渐开线形成过程中圆锥的展角,
为球面渐开线形成过程中平面的展角,
为圆锥的基锥角。由弧长公式可知:
。
2.2.2. 抛物线锥齿轮模型构建
锥齿轮的齿线是空间曲线,随着基锥角的改变,同一种线形也会有所变化。平面曲线缠绕在锥面上,使其转化为空间曲线。将抛物线的坐标系原点放在锥齿轮齿厚的中面上,抛物线的横坐标L对应锥面齿线距平面坐标系的纵轴的弧长,如图3所示。
由弧长公式可知弧长L、母线长度Rb、基锥角
和分度角
存在以下关系:
(6)
(7)
其中Ro为基圆锥原点到平面坐标系原点的距离,h为抛物线方程的纵坐标,基锥角
为定值,弧长L与h有关,因此可知分度角只与抛物线方程的纵坐标h有关。
齿轮参数如表1所示,针对抛物线齿形的球面渐开线锥齿轮建模,利用UG二次开发,通过齿线方程和齿廓方程实现抛物线锥齿轮的快速建模。

Table 1. The basic parameters of the gear
表1. 齿轮的基本参数
针对抛物线锥齿轮,由抛物线方程Y2 = 2PX知焦准距P决定了齿面齿形,通过不同的焦准距得到不同的齿面,齿面如图4所示。
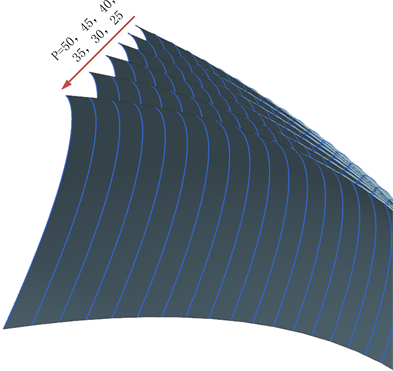
Figure 4. Parabolic bevel gear tooth surface
图4. 抛物线锥齿轮齿面
通过UG二次开发实现齿轮的快速建模,只需改变一个参数即可快速构建所需要的齿轮模型,为该齿形的仿真分析提供可靠的数字化模型。焦准距为30的抛物线锥齿轮装配模型如图5所示。

Figure 5. Parabolic bevel gear assembly model
图5. 抛物线锥齿轮装配模型
3. 抛物线锥齿轮仿真分析
本文针对抛物线齿形球面渐开线锥齿轮,利用UG二次开发快速构建齿轮模型,分析在不同的齿向修形情况下的抛物线锥齿轮轴向力的变化以及齿轮啮合情况与啮合区应力应变情况。以焦准距为30和40的抛物线锥齿轮为例进行静力学分析。
3.1. 静力学分析流程
3.1.1. 导入模型
将抛物线锥齿轮装配正确后以STP格式保存,利用Ansys Workbench仿真分析软件,使用Workbench静力学分析模块,选择齿轮模型并导入。
3.1.2. 定义接触面
齿轮模型导入分析软件Workbench的DM模块,此时大小轮模型会自动生成接触对,此时的接触对不能满足本分析所需,过少的接触对限制会发生穿透,引发错误,影响分析结果。删除自动生成的接触对,设置齿轮的接触面为两轮的所有凹凸面,选中主动轮的凹面和凸面,将所有的接触面并命名为01,同样的方法设置从动轮的接触面并命名为02。
3.1.3. 接触设置
属性设置中,接触面为01,目标面为02,为了提高计算结果的准确性,将接触类型设置为摩擦接触,摩擦系数设置为0.2。计算方法选择拉格朗日算法,拉格朗日算法可以减少求解过程中对刚度的敏感度。大齿轮内孔轴添加传动铰链,接触类型设置为实体对地,铰接类型设置为转动。其余默认。
3.1.4. 网格划分
有限元分析中,划分的网格质量对结果的准确性起决定性因素,只有建立高精度的有限元网格模型分析才能得到准确的数值分析,为了使结果更加精确和运算的效率,采用整体自动划分和接触面细化的方法对模型进行网格划分。
3.1.5. 施加约束与载荷
在静力学分析时,假设两齿轮接触瞬间,从动轮固定不动,主动轮以给定的角速度旋转,施加约束时,对从动轮内轴孔面施加固定约束,主动轮内轴孔面施加1000 N·m扭矩。操作如下:在静态结构中,插入固定约束,添加小轮内轴孔为固定约束面。插入转动副,设置转矩数值为1000 N·m。
3.1.6. 求解
通过Ansys Workbench软件计算出抛物线锥齿轮的径向力X、径向力Y、轴向力Z。为了得到所需要的解结果,需在求解结果中插入探针,通过反作用力计算得到数据结果。在求解结果中插入等效应力,等效弹性应变和总变形量,并查看结果。
3.2. 齿轮静力学结果分析
利用Ansys Workbench分析齿轮啮合情况与齿轮轴向力,得到如图6(a)所示的等效应力图和如图6(b)所示的轴向力数据图。
由图6可知,在修形行前,应力集中在小端切两齿面啮合区分别靠近齿根和齿顶,修形后偏向齿顶的接触区下移,偏向齿根的接触区上移,同时,在轴端部分的接触应力减小,接触区向齿轮中间靠拢,使得接触应力得到改善,提升传动性能。
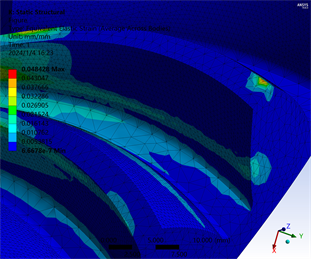
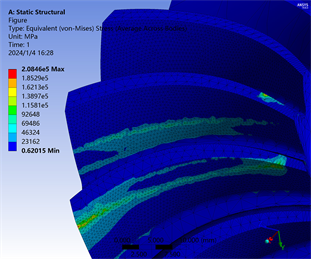 (a) 修形前等效应力图 (b) 修形后等效应力图
(a) 修形前等效应力图 (b) 修形后等效应力图
Figure 6. Equivalent force diagram of parabolic bevel gear before and after reshaping
图6. 抛物线锥齿轮修形前后等效应力图

Table 2. Axial force simulation results
表2. 轴向力仿真结果
由表2可知,抛物线锥齿轮的在轴向力方向上的分力相互抵消,从而使得合力变小。将抛物线锥齿轮和格里森进行对比。由于装配的原因,其抛物线锥齿轮和格里森数值存在偏差,因此不将X轴方向分力的大小作为参考标准,只考虑Y轴与Z轴方向上的力的大小的差值来衡量抛物线锥齿轮相对于格里森齿轮的优势。
在修形前由于抛物线齿形的齿向曲率较小,导致在轴向方向的分力抵消趋势较小,在进行修形后,随着啮合区的调整分力抵消趋势逐渐增大,由修形前的−7.846,变为1.284 (这里的正负号只代表方向,不代表数值大小)。由此可知,抛物线锥齿轮在Z轴可抵消部分力,从而提高其承载性能。在受到相同力的作用下,抛物线锥齿轮相较于格里森齿轮在齿向方向上承载能力强,在齿轮传动性能上具有优势。
4. 结论
本文针对抛物线球面渐开线锥齿轮,通过剖析球面渐开线的形成原理构建球面渐开线方程,利用平面曲线的空间变换获得缠绕在基圆锥表面的齿线,结合UG二次开发快速构建齿轮模型。通过更改齿线方程,实现齿向修形。探究了齿向修形对抛物线锥齿轮的影响,通过利用Workbench对抛物线锥齿轮修形前后的模型仿真分析得出结论:抛物线锥齿轮的在轴向方向上的分力可以相互抵消,从而使得合力变小。在进行修形后,随着啮合区的调整,分力抵消趋势逐渐增大,由修形前的−7.846,变为1.284。由此可知,抛物线锥齿轮在Z轴可抵消部分力,从而提高其承载性能。
本文实现了抛物线锥齿轮由设计到模型创建的整个过程,结合UG二次开发,将设计过程简化。为新型锥齿轮设计提供了思路。提高研究人员的工作效率,缩短新型锥齿轮研发周期。同时验证了模型的正确性。
基金项目
国家自然科学基金(52227809),项目名称:小模数齿轮超精密测量仪器研制。
参考文献
NOTES
*通讯作者。