基于Pythagorean Hodograph T-曲线的过渡曲线的构造

Construction of Transition Curve Based on Pythagorean Hodograph T-Curve

摘要: 本文基于平面三次T-Bézier曲线，定义了三次T-PH曲线，研究了T-PH曲线的代数和几何特征，进而利用三次T-PH曲线构造了两圆互不包含的情况下的C型过渡曲线，给出圆心距的取值范围，并证明了过渡曲线的唯一性。最后给出数值实例，验证了方法的可行性。

Abstract: In this paper, we define the cubic T-PH curve and study the algebra and geometric characteristic of T-PH curve. In addition, a non-circle transition curve is constructed as a C-type transition curve us-ing cubic T-PH curve, giving the value range of the center distance, and proving the uniqueness of transition curve. Finally, numerical examples are given to verify the feasibility of the method.

1. 引言

Pythagorean-Hodograph (PH)曲线是Farouki [1] 提出的一种特殊的多项式参数曲线。由于PH曲线的曲率和等距曲线是有理形式的，因此被广泛应用在计算机辅助设计、机器人行走路线、数控机器加工等领域中。

到目前为止，基于一元多项式空间 $\left\{1,t,\cdots ,t^{n-2},t^{n-1},t^n\right\}$ 中的PH曲线已经有了比较深入的研究。文献 [1] 给出了在边角分离的条件下，三次PH曲线的控制多边形的几何特征。但是有理式Bézier模型不能准确地表示超越曲线，因此，许多学者提出了三角空间和代数双曲混合空间。文献 [2] 定义了空间 $\left\{1,t,\cdots ,t^{n-2},\sin t,\cos t\right\}$ 上的C-Bézier曲线，并给出三次C-Bézier曲线成为PH曲线的充要条件；文献 [3] 以三次PH-C曲线的代数结构为基础，给出三次PH-C曲线的几何特征及构造方法。文献 [4] 定义了 $\left\{1,t,\cdots ,t^{n-2},\sinh t,\cosh t\right\}$ 上的AH-Bézier曲线，文献 [5] 在文献 [4] 的基础上，通过两种基底推导出三次PH-H曲线的充要条件，并给出PH-H曲线的几何构造方法；文献 [6] 定义了在三角多项式空间 $\left\{1,\sin t,\cos t,\cdots ,\sin nt,\cos nt\right\}$ 上的T-Bézier曲线。目前三角多项式空间上的PH曲线尚无研究。

在曲线曲面的几何造型设计中，经常涉及到2条曲线间的光滑拼接，即过渡曲线的构造。由于过渡曲线要求在端点处满足几何连续性，并且曲线的曲率单调变化，因此文献 [7] 定义了用积分表示的Clothoid曲线，并将其用于公路铁路设计中。后来发现Clothoid曲线的表达式中含有Fresnel积分，计算复杂，许多学者开始对文献 [8] 提出了用三次Bézier曲线构造过渡曲线，但Bézier曲线的弧长和等距线不能表示为有理形式，在实际的几何设计中存在新的难题，为解决这一问题，文献 [9] [10] [11] 提出了利用五次PH曲线构造过渡曲线，五次PH曲线的内部不含奇点和拐点，其曲率单调，并且曲率和等距曲线是有理形式的，因此更适用于构造过渡曲线。为了使过渡曲线构造更为简单高效，文献 [12] 利用放缩法得到了类三次Bézier螺线，并构造了半径比例不受限制的两圆弧间S型和C型G²连续过渡曲线；文献 [13] [14] [15] 分别构造了C-Bézier螺线、H-Bézier螺线和T-Bézier螺线，并利用这些螺线作两圆之间的过渡曲线。为了避免求解复杂的非线性方程组，文献 [16] 采用次数较低的三次PH曲线构造相互包含的两圆弧间G²连续过渡曲线，文献 [17] 基于三次PH曲线，构造了两圆不相互包含的情况下的C型过渡曲线。

本文主要研究了T-PH曲线的代数和几何特征，并用来解决过渡曲线的构造问题。结构安排如下：首先，给出T-PH曲线的定义，并应用平面参数曲线的复数表示法，讨论T-PH曲线的代数结构和几何特征；其次，基于三次T-PH曲线来构造不互相包含的两圆之间的C型过渡曲线，并证明了过渡曲线的唯一性；最后，给出数值实例。

2. T-PH曲线

在三角多项式空间 $\Gamma =span\left\{1,\sin t,\cos t,\cos 2t\right\}$ 中可以生成一类特殊曲线T-Bézier曲线。

定义1 [7] 给定平面上一组控制顶点 $P_i\left(i=0,1,2,3\right)\in R^2$ ，对于任意的 $t\in \left[0,\frac{\pi }{2}\right]$ ，三次T-Bézier曲线表示为

$P\left(t\right)={\displaystyle \underset{i=0}{\overset{3}{\sum }}{P}_i}{Z}_{i,3}\left(t\right)$ (1)

其中 $Z_{i,3}\left(t\right)$ 为T-Bézier曲线的基函数。其矩阵表示形式为

$P\left(t\right)=\left(\begin{array}{cccc}1& \sin t& \cos t& \cos 2t\end{array}\right)\left(\begin{array}{cccc}\frac{3}{2}& -1& -1& \frac{3}{2}\\ -2& 2& 0& 0\\ 0& 0& 2& -2\\ -\frac{1}{2}& 1& -1& \frac{1}{2}\end{array}\right)\left(\begin{array}{c}{P}_0\\ P_1\\ P_2\\ P_3\end{array}\right)$

显然

$\begin{array}{l}{Z}_{0,3}\left(t\right)=\frac{3}{2}\hfill \end{array}-2\sin t-\frac{1}{2}\cos 2t$

$Z_{1,3}\left(t\right)=-1+2\sin t+\cos 2t$

$Z_{2,3}\left(t\right)=-1+2\cos t-\cos 2t$

$Z_{3,3}\left(t\right)=\frac{3}{2}-2\cos t+\frac{1}{2}\cos 2t$

则有

$P\left(t\right)=P_0+{\displaystyle \underset{i=0}{\overset{2}{\sum }}\Delta P_i}{\displaystyle \underset{j=i+1}{\overset{3}{\sum }}{Z}_{j,3}(\; t\; )}$

从而

$P^{\prime }\left(t\right)=\Delta P_0{w}_0+\Delta P_1{w}_1+\Delta P_2{w}_2,$ (2)

其中

$w_i={\displaystyle \underset{j=i+1}{\overset{3}{\sum }}{Z^{\prime }}_{j,3}}\left(t\right),i=0,1,2$

记 $w=\left(\begin{array}{c}{w}_0\\ w_1\\ w_2\end{array}\right)=\left(\begin{array}{c}2\cos t\left(1-\sin t\right)\\ 2\sin t\left(1-\cos t\right)\\ 2\sin t\cos t\end{array}\right)$ 。

定义2平面T-Bézier曲线 $P\left(t\right)=\left(x\left(t\right),y\left(t\right)\right)\in {\Gamma }_n$ ，若存在 $\sigma \left(t\right)\in {\Gamma }_{n-1}$ 使得其导数分量 $x^{\prime }\left(t\right),y^{\prime }\left(t\right)$ 满足 ${x^{\prime }}^2\left(t\right)+{y^{\prime }}^2\left(t\right)={\sigma }^2\left(t\right)$ ，则称该曲线为Pythagorean Hodograph T-曲线，简称T-PH曲线。

3. 三次T-PH曲线的代数与几何特征

定理1 若参数曲线 $P\left(t\right)=\left(x\left(t\right),y\left(t\right)\right)$ 满足：

$\{\begin{array}{l}{x}^{\prime }\left(t\right)=w\left(t\right)\left[u^2\left(t\right)-v^2\left(t\right)\right]\hfill \\ y^{\prime }\left(t\right)=2w\left(t\right)u\left(t\right)v(\; t\; )\hfill \end{array}$

其中 $w\left(t\right),u\left(t\right),v\left(t\right)$ 分别为实系数多项式，且不等于零，则 $P\left(t\right)$ 为PH曲线。

根据定义2和定理1，可以得到

定理2 式(1)中的三次T-Bézier曲线 $P\left(t\right)$ 是PH曲线的充要条件是存在实数 $u_0,v_0,u_1,v_1$ ，使得其控制顶点满足如下关系式

$\{\begin{array}{l}{P}_1=P_0+\left(\frac{u_1^2-v_1^2}{2},u_1{v}_1\right)\hfill \\ P_2=P_1+\left(\frac{u_1^2-v_1^2+u_0{u}_1-v_0{v}_1}{2},\frac{2u_1{v}_1+u_0{v}_1+u_1{v}_0}{2}\right)\hfill \\ P_3=P_2+\left(\frac{u_0{u}_1-v_0{v}_1}{2},\frac{u_0{v}_1+u_1{v}_0}{2}\right)\hfill \end{array}$ (3)

其中

$\{\begin{array}{l}{u}_0^2+u_1^2=v_0^2+v_1^2\hfill \\ u_0{v}_0+u_1{v}_1=0\hfill \end{array}$ (4)

证明：令

$\{\begin{array}{l}u\left(t\right)=u_0\sin \frac{t}{2}+u_1\cos \frac{t}{2}\\ v\left(t\right)=v_0\sin \frac{t}{2}+v_1\cos \frac{t}{2}\end{array}$

由T-Bézier曲线的基函数得

$u^2\left(t\right)-v^2\left(t\right)=\left(\frac{u_1^2-u_0^2}{2}-\frac{v_1^2-v_0^2}{2}\right)\cos t+\left(u_0{u}_1-v_0{v}_1\right)\sin t+\left(\frac{u_0^2+u_1^2}{2}-\frac{v_0^2+v_1^2}{2}\right)$

$2u\left(t\right)v\left(t\right)=\left(u_1{v}_1-u_0{v}_0\right)\cos t+\left(u_0{v}_1+u_1{v}_0\right)\sin t+\left(u_0{v}_1+u_1{v}_1\right)$

三次T-Bézier曲线的导数可写为

$P^{\prime }\left(t\right)=2\left(P_1-P_0\right)\cos t+\left(P_0-2P_1+2P_2-P_3\right)\sin 2t+2\left(P_3-P_2\right)\sin t$

因此得到T-PH曲线的控制顶点：

$\{\begin{array}{l}{P}_0=\left(x_0,y_0\right)\hfill \\ P_1=P_0+\left(\frac{u_1^2-u_0^2-v_1^2+v_0^2}{4},\frac{u_1{v}_1-u_0{v}_0}{2}\right)\hfill \\ P_2=P_1+\left(\frac{u_1^2-u_0^2-v_1^2+v_0^2+2u_0{u}_1-2v_0{v}_1}{4},\frac{u_1{v}_1-u_0{v}_0+u_0{v}_1+u_1{v}_0}{2}\right)\hfill \\ P_3=P_2+\left(\frac{u_0{u}_1-v_0{v}_1}{2},\frac{u_0{v}_1+u_1{v}_0}{2}\right)\hfill \end{array}$

其中 $u_0,v_0,u_1,v_1$ 需满足

$\{\begin{array}{l}{u}_0^2+u_1^2=v_0^2+v_1^2\hfill \\ u_0{v}_0+u_1{v}_1=0\hfill \end{array}$

对上式进行整理即可得到式(3)，从而得到了三次T-Bézier曲线成为T-PH曲线的充要条件。

下面将用一个例子来说明定理2，用定理中的充要条件给定参数取值，计算出曲线的控制顶点，并根据T-Bézier曲线的表达式构造出两条三次T-PH曲线。

例1给定 $P_0=\left(0,0\right),u_0=1,u_1=2,v_0=2,v_1=-1$ ，则由式(3)可得三次T-PH曲线的控制顶点为：

$\begin{array}{l}{P}_0=\left(0,0\right),P_1=\left(1.5,-2\right)\\ P_2=\left(5,-2.5\right),P_3=\left(7,-1\right)\end{array}$

得到的三次T-PH曲线及其控制多边形如图1所示。

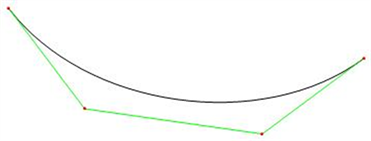
Figure 1. Cubic T-PH curve and control polygon

图1. 三次T-PH曲线及控制多边形

Farouki已经得出三次多项式PH曲线具有简单的几何性质，利用这个性质可以对三次多项式PH曲线进行判别和构造，接下来将证明三次T-PH曲线也具有类似的几何性质。

定理3 若 $P_i,i=0,1,2,3$ 为三次T-Bézier曲线 $P\left(t\right)$ 的控制顶点， ${\theta }_i,i=0,1$ 为控制多边形的两个内角， $L_i=\Vert \Delta P_i\Vert ,i=0,1,2$ 为控制多边形的三条边长，则 $P\left(t\right)$ 是T-PH曲线当且仅当

${\theta }_0={\theta }_1,L_1^2=2L_0{L}_2$ (5)

证明：由定理2可知，若一条三次T-Bézier曲线为T-PH曲线，则存在实数 $u_0,v_0,u_1,v_1$ 使得式(3)、(4)成立。记 ${\phi }_i,i=0,1,2$ 为 $\Delta P_i$ 的辐角，可得

$\Delta P_0=L_0{\text{e}}^{i{\phi }_0}=\frac{u_1^2-v_1^2}{2}+u_1{v}_{1}i$ (6)

$\Delta P_1=L_1{\text{e}}^{i{\phi }_1}=\frac{u_1^2-v_1^2+u_0{u}_1-v_0{v}_1}{2}+\frac{2u_1{v}_1+u_0{v}_1+u_1{v}_0}{2}i$ (7)

$\Delta P_2=L_2{\text{e}}^{i{\phi }_2}=\frac{u_0{u}_1-v_0{v}_1}{2}+\frac{u_0{v}_1+u_1{v}_0}{2}i$ (8)

分别计算 $\Delta P_1^2$ 和 $\Delta P_0\Delta P_2$ 的实部和虚部，得到

$\begin{array}{l}\mathrm{Re}\left(\Delta P_0\Delta P_2\right)=\frac{u_1^3{u}_0+v_1^3{v}_0-3u_1^2{v}_0{v}_1-3v_1^2{u}_0{u}_1}{4}\\ \mathrm{Re}\left(\Delta P_1^2\right)=\frac{\varphi \left(u_0,u_1,v_0,v_1\right)+2u_1^3{u}_0+2v_1^3{v}_0-6u_1^2{v}_0{v}_1-6v_1^2{u}_0{u}_1}{4}\end{array}$

其中 $\varphi \left(u_0,u_1,v_0,v_1\right)=u_1^4-6u_1^2{v}_1^2-4u_0{u}_1{v}_0{v}_1+v_1^4+u_0^2{u}_1^2+v_0^2{v}_1^2-u_0^2{v}_1^2-u_1^2{v}_0^2$

由式(4)化简得到 $\varphi \left(u_0,u_1,v_0,v_1\right)=0$

$\begin{array}{l}\mathrm{Im}\left(\Delta P_0\Delta P_2\right)=\frac{u_1^3{v}_0-v_1^3{u}_0+3u_1^2{u}_0{v}_1-3v_1^2{u}_1{v}_0}{4}\\ \mathrm{Im}\left(\Delta P_1^2\right)=\frac{\psi \left(u_0,u_1,v_0,v_1\right)+u_1^3{v}_0-v_1^3{u}_0+3u_1^2{u}_0{v}_1-3v_1^2{u}_1{v}_0}{2}\end{array}$

其中 $\psi \left(u_0,u_1,v_0,v_1\right)=2u_1^3{v}_1-2v_1^3{u}_1+u_0^2{u}_1{v}_1+u_1^2{u}_0{v}_0-v_1^2{u}_0{v}_0-v_0^2{u}_1{v}_1$

由式(4)化简得到 $\psi \left(u_0,u_1,v_0,v_1\right)=0$

从而可得

$\frac{{\Vert \Delta P_1\Vert }^2}{\Delta P_0\Delta P_2}=2$ (9)

因为 ${\theta }_i$ 为控制多边形的内角，即 ${\theta }_i={\phi }_{i+1}-{\phi }_i$ ，所以由式(9)可知式(5)成立。

反之，若对于给定的三次T-PH曲线，其控制多边形满足式(5)，则假定 $u_0,u_1,v_0,v_1$ 为待定系数，使得式(6)~式(8)成立。若式(6)、式(7)成立，则式(8)也成立。因此分别考虑复方程(6)的实部和虚部，通过求解线性方程组得到

$u_1^2=\Vert \Delta P_0\Vert +\mathrm{Re}\left(\Delta P_0\right),v_1^2=\frac{{\mathrm{Im}}^2\left(\Delta P_0\right)}{\Vert \Delta P_0\Vert +\mathrm{Re}\left(\Delta P_0\right)}$

进一步，将 $u_1,v_1$ 作为已知量，分别考虑复方程(7)的实部和虚部，通过求解线性方程组得到

$u_0=\frac{2\left(u_1\mathrm{Re}\left(\Delta P_1\right)+v_1\mathrm{Im}\left(\Delta P_1\right)\right)-u_1^3-u_1{v}_1^2}{u_1^2+v_1^2}$

$v_0=\frac{2\left(v_1\mathrm{Re}\left(\Delta P_1\right)-u_1\mathrm{Im}\left(\Delta P_1\right)\right)+v_1^3+u_1^2{v}_1}{u_1^2+v_1^2}$

综上，得到使定理3成立的4个实数 $u_0,u_1,v_0,v_1$ ，因此，该曲线是一条三次T-PH曲线。证毕。

4. 三次T-PH过渡曲线的构造

平面参数曲线的曲率表达式为：

$k\left(t\right)=\frac{\left|P^{\prime }\left(t\right)\times P^{″}\left(t\right)\right|}{{\left|P^{\prime }\left(t\right)\right|}^3}$

设三次T-PH曲线的控制多边形初始端点为P₀，末端点为P₃，以P₀为原点建立直角坐标系，由P₀处的曲率可得到以C₀为圆心，r₀为半径的圆Ω₀，由P₃的曲率可得到以C₁为圆心，r₁为半径的圆Ω₁，如图2所示。

Figure 2. Circle of curvature [17]

图2. 曲率圆 [17]

由图2得三次T-PH曲线的控制顶点为：

$\{\begin{array}{l}{P}_0=\left(0,0\right)\hfill \\ P_1=\left(L_0,0\right)\hfill \\ P_2=\left(L_0+L_1\cos \theta ,L_1\sin \theta \right)\hfill \\ P_3=\left(L_0+L_1\cos \theta +L_2\cos 2\theta ,L_1\sin \theta +L_2\sin 2\theta \right)\hfill \end{array}$ (10)

将式(10)代入式(1)中，得到 $P\left(t\right)$ 的参数表达式为：

$\begin{array}{c}P\left(t\right)=\left(x\left(t\right),y\left(t\right)\right)\\ =P_0\left(\frac{3}{2}-2\sin t+\cos 2t\right)+P_1\left(-1+2\sin t+\cos 2t\right)\\ +P_2\left(-1+2\cos t-\cos 2t\right)+P_3\left(\frac{3}{2}-2\cos t+\frac{1}{2}\cos 2t\right)\end{array}$

其中

$\begin{array}{c}x\left(t\right)=L_0\left(-1+2\sin t+\cos 2t\right)+\left(L_0+L_1\cos \theta \right)\left(-1+2\cos t-\cos 2t\right)\\ +\left(L_0+L_1\cos \theta +L_2\cos 2\theta \right)\left(\frac{3}{2}-2\cos t+\frac{1}{2}\cos 2t\right)\end{array}$ (11)

$y\left(t\right)=L_1\sin \theta \left(-1+2\cos t-\cos 2t\right)+\left(L_1\sin \theta +L_2\sin 2\theta \right)\left(\frac{3}{2}-2\cos t+\frac{1}{2}\cos 2t\right)$ (12)

对式(11)、式(12)求导，得到T-PH曲线导数的模长为

$\left|P^{\prime }\left(t\right)\right|=L_0\left(2\cos t-\sin 2t\right)+L_1\cos \theta \sin 2t+L_2\left(2\sin t-\sin 2t\right)$

则曲率表达式为

$k\left(t\right)=\frac{2\sqrt{2L_0{L}_2}\sin \theta }{{\left(L_0\left(2\cos t-\sin 2t\right)+\sqrt{2L_0{L}_2}\cos \theta \sin 2t+L_2\left(2\sin t-\sin 2t\right)\right)}^2}$ (13)

将 $t=0,\frac{\pi }{2}$ 代入式(13)分别得到初始端点和末端点的曲率 $k_0$ 和 $k_1$

$\begin{array}{l}{k}_0=k\left(0\right)=\frac{\sqrt{2L_0{L}_2}\sin \theta }{2L_0^2}\\ k_1=k\left(\frac{\pi }{2}\right)=\frac{\sqrt{2L_0{L}_2}\sin \theta }{2L_2^2}\end{array}$

因为 $0<\theta <\frac{\pi }{2}$ ，所以 $k_0$ 和 $k_1$ 同号，因此当两个圆互不包含时，所构造的三次PH过渡曲线是C型的。

设 $r_0$ 、 $r_1$ 为是末端点的曲率半径， $r_0>r_1$ 令 $\lambda =\sqrt{\frac{L_2}{L_0}}=\sqrt[4]{\frac{r_1}{r_0}}=\sqrt{\frac{k_0}{k_1}}$ 则 $0<\lambda <1$ 。

定理4 当 $r>r_0-r_1$ 时，即两圆不互相包含时，若

$0<\cos \theta <\frac{\sqrt{2}}{2}\lambda$

则过渡曲线是一个C型过渡曲线。

证明：对式(13)求导，得到三次T-PH曲线的曲率导数为

$k^{\prime }\left(t\right)=\frac{-8\sqrt{2L_0{L}_2}\sin \theta \left(L_0\sin t-L_2\cos t+\left(L_0-\sqrt{2L_0{L}_2}\cos \theta +L_2\right)\cos 2t\right)}{{\left(L_0\left(2\cos t-\sin 2t\right)+\sqrt{2L_0{L}_2}\cos \theta \sin 2t+L_2\left(2\sin t-\sin 2t\right)\right)}^3}$ (14)

则

$\begin{array}{l}{k}^{\prime }\left(0\right)=\frac{-\sqrt{2L_0{L}_2}\sin \theta \left(L_0-\sqrt{2L_0{L}_2}\cos \theta \right)}{L_0^3}\\ k^{\prime }\left(1\right)=\frac{-\sqrt{2L_0{L}_2}\sin \theta \left(\sqrt{2L_0{L}_2}\cos \theta -L_2\right)}{L_2^3}\end{array}$

得

$k^{\prime }\left(0\right)\cdot k^{\prime }\left(1\right)=\frac{2L_0{L}_2{\sin }^2\theta \left(L_0-\sqrt{2L_0{L}_2}\cos \theta \right)\left(\sqrt{2L_0{L}_2}\cos \theta -L_2\right)}{{\left(L_0{L}_2\right)}^3}$

由于 $\lambda =\sqrt{\frac{L_2}{L_0}}=\sqrt[4]{\frac{r_1}{r_0}}$ ， $0<\lambda <1$ ，故当 $0<\cos \theta <\frac{\sqrt{2}}{2}\lambda$ 时，

$\left(L_0+L_2\right)\sqrt{2L_0{L}_2}\cos \theta -L_0{L}_2\left(1+2{\cos }^2\theta \right)<0,$

即 $k^{\prime }\left(0\right)\cdot k^{\prime }\left(1\right)<0$ ，此时，三次T-PH曲线的内部含有尽量少的曲率极值点，且所构造的三次T-PH曲线是C型G²连续的过渡曲线。

下面讨论三次T-PH过渡曲线的唯一性。

定理5 设给定端点的曲率为 $k_0$ 和 $k_1$ ，相应的曲率半径为 $r_0$ 和 $r_1$ ，令 $\lambda =\sqrt[4]{\frac{r_1}{r_0}}$ ，若

$0.6719<\lambda <1$

且

$r_0-r_1<r<q\left(\lambda \right)\left(r_0-r_1\right)$

其中

$q\left(\lambda \right)=\sqrt{\frac{2{\lambda }^8-3{\lambda }^6+4{\lambda }^4-3{\lambda }^2+2}{2{\left(1-{\lambda }^4\right)}^2}}$

若所构造的三次T-PH过渡曲线符合上述条件，则该曲线是唯一的。

证明：由图2知，两圆的圆心分别为 $C_0\left(0,r_0\right)$ ， $C_1\left(x_3-r_1\sin 2\theta ,y_3+r_1\cos 2\theta \right)$ ，则圆心距 $\stackrel{\to }{C_0{C}_1}=C_1-C_0=\left(x_3-r_1\sin 2\theta ,y_3+r_1\cos 2\theta -r_0\right)$ ，设圆心距长度为r，则 $\left|C_1-C_0\right|=r$ 。

由始末端点曲率 $k_0$ 和 $k_1$ 及 $\lambda =\sqrt[4]{\frac{r_1}{r_0}}$ 可得

$L_0=\frac{\sqrt{2}}{2}\lambda r_0\sin \theta ,$ (15)

$L_2=\frac{\sqrt{2}}{2}{\lambda }^3{r}_0\sin \theta ,$ (16)

由 $L_1=\sqrt{2L_0{L}_2}$ ，得

$L_1={\lambda }^2{r}_0\sin \theta$ (17)

构造函数 $g\left(\theta \right)={\left|C_1-C_0\right|}^2-r^2$ ，令 $h=\cos \theta$ ，则 $0<h<1$ 。将式(10)中T-PH曲线的控制顶点代入 $g\left(\theta \right)$ 中，得到关于h的方程

$\begin{array}{c}g\left(h\right)=-2{\lambda }^4{r}_0^2{h}^4+\sqrt{2}{\lambda }^3{r}_0^2\left({\lambda }^2+1\right)h^3+\frac{3}{2}{\lambda }^2{r}_0^2\left(\left({\lambda }^4-\frac{4}{3}{\lambda }^2+1\right)+1\right)h^2\\ -\sqrt{2}{\lambda }^3{r}_0^2\left({\lambda }^2+1\right)h+r_0^2\left({\lambda }^8-\frac{3}{2}{\lambda }^6+2{\lambda }^4-\frac{3}{2}{\lambda }^2+1\right)-r^2\\ =0\end{array}$

因为 $0<h=\cos \theta <\frac{\sqrt{2}}{2}\lambda$ ，考虑 $g\left(h\right)$ 在 $\left(0,\frac{\sqrt{2}}{2}\lambda \right)$ 上的情况：

$\begin{array}{l}g\left(\frac{\sqrt{2}}{2}\lambda \right)=\frac{9{\lambda }^8-10{\lambda }^6+11{\lambda }^4-6{\lambda }^2+4}{4{\left(1-{\lambda }^4\right)}^2}{\left(r_1-r_0\right)}^2-r^2，\\ g\left(0\right)=\frac{2{\lambda }^8-3{\lambda }^6+4{\lambda }^4-3{\lambda }^2+2}{2{\left(1-{\lambda }^4\right)}^2}{\left(r_1-r_0\right)}^2-r^2，\end{array}$

由零点定理， $g\left(h\right)=0$ 有解的充分条件为 $g\left(0\right)\cdot g\left(\frac{\sqrt{2}}{2}\lambda \right)<0$ 。

由 $0<\lambda <1$ 得 $0<\frac{\sqrt{9{\lambda }^8-10{\lambda }^6+11{\lambda }^4-6{\lambda }^2+4}}{2\left(1-{\lambda }^4\right)}<1$ ，因为 $r>r_0-r_1$ ，所以 $g\left(\frac{\sqrt{2}}{2}\lambda \right)<0$ ，从而 $g\left(0\right)>0$ 。

经计算，当 $0.6719<\lambda <1$ 时， $g\left(0\right)>0$ 成立，此时 $g\left(h\right)$ 在 $\left(0,\frac{\sqrt{2}}{2}\lambda \right)$ 有根。

Figure 3. Cubic T-PH transition curves between two circles that do not contain each other

图3. 互不包含的两圆之间的三次T-PH过渡曲线

接下来讨论h的唯一性：

$g^{″}\left(h\right)$ 是关于h的二次多项式，且开口向下，另外 $g^{″}\left(\frac{\sqrt{2}}{2}\lambda \right)=3{\lambda }^2{r}_0^2\left(\frac{2}{3}{\lambda }^2+1\right)>0$ ， $g^{″}\left(0\right)=3{\lambda }^2{r}_0^2\left({\left({\lambda }^2-\frac{2}{3}\right)}^2+\frac{5}{9}\right)>0$ ，所以 $g^{\prime }\left(h\right)$ 是增函数，又 $g^{\prime }\left(0\right)<0$ ， $g\left(0\right)>0$ ， $g\left(\frac{\sqrt{2}}{2}\lambda \right)<0$ ，因此 $g\left(h\right)$ 在 $\left(0,\frac{\sqrt{2}}{2}\lambda \right)$ 有唯一的根。

5. 数值例子

取 $P_0\left(0,0\right)$ ， $r_0=1.5$ ，由 $0.6719<\lambda <1$ ，取 $r_1=1$ ，计算得出过渡曲线两端点的曲率圆的圆心距范围为 $r_0-r_1<r<q\left(\lambda \right)\left(r_0-r_1\right)$ ，取 $r=2.5\left(r_0-r_1\right)$ ，解得 $\theta =1.5484$ ，生成的三次T-PH过渡曲线如图3所示。

6. 总结

本文基于三角多项式空间，给出了三次T-Bézier曲线成为T-PH曲线的几何特征。本文研究的另一个问题，即利用三次T-PH曲线的几何特征，构造了互不包含的两圆之间的三次T-PH过渡曲线，由于过渡曲线次数较低，所以计算方便，易在CAD中实现。

NOTES

^*通讯作者。