1. 引言
由于温室效应不断积累 [1] ,变暖是全球气候变化的一个重要趋势。人们又发现进入21世纪以来,10年间全球全年平均气温上升仅为0.03℃。这种现象被称为全球变暖停滞现象 [2] 。该现象引起了公众对全球变暖的注意。因此,对全球温度变化进行分析和预测有非常重要的意义。研究全球温度变化需要长时间的观测积累,然而过去收集的数据并不完整,这给统计分析带来了很大的困难。
目前为止,国内外很多学者已经提出了很多气象预测的方法,比较主要的方法有三种 [3] 。第一种是天气学方法,该方法是预测者根据自己对气象知识的了解以及个人经验,对一定期限内的天气进行预测。这种方法充分利用了已有的天气状况,但这种方法对气象数据分析非常少,更多地依靠气象人员的经验,因此会导致误差比较大 [4] 。第二种是统计分析方法,该方法首先利用已有的天气数据得到各种天气属性之间的关联程度,再运用有关的数学原理推导出更好的预测模型,最后利用所得的模型对未来天气进行预测 [5] 。第三种是机器学习方法。除了使用天气学和统计分析方法,气象预测人员也越来越多地采用机器学习算法来进行预测,常用的算法主要包括神经网络,支持向量机,贝叶斯算法等 [6] 。
大气系统比较复杂,因此要准确模拟它的变化情况相当困难。由于结合统计分析方法和机器学习方法能够实现较好的预测精度,因此基于统计分析和机器学习的预测模型已不断成为气温预测的主要方法,如邹平 [7] 等结合时间序列方法和BP神经网络对土壤温度数据进行了分析和预测,所得的结论为作物合理布局提供了重要的指导依据。朱晶晶 [8] 利用基于SVM的回归预测模型对海南省各市县的月平均气温数据进行了分析和预测,研究结果表明该论文提出的基于SVM的回归预测模型在短期气温预测方面具有很好的预报能力。刘红 [9] 将随机森林算法用于温室内气温的预测,所得结论发现随机森林模型的预测精度明显优于其他模型。Fan Linan [10] 等利用一种基于改进支持向量机方法构建了一个温室温度预测模型。与传统的BP神经网络预测模型相比,利用改进的支持向量机得到的预测模型预测效果更佳,在预测精度上有了显著的提高。Rujian Qiu [11] 等利用一种改进的人工神经网络方法对长江水温进行了分析和预测,得到了比较理想的预测结果。宋春山 [12] 等人利用对黑龙江漠河段的日平均气温数据进行了分析研究,并进一步利用所得的基于BP神经网络的预测模型对2021年和2022年的开江期日平均气温变化情况进行了预测。
目前,利用深度卷积长短期记忆网络模型(CNN-LSTM)对全球年平均气温的研究还不完善。本文根据气温时间序列构建ARIMA自回归时间序列预测模型和深度卷积长短期记忆网络模型(CNN-LSTM)对全球年平均气温进行了分析和预测。
2. 研究设计
2.1. 数据来源
本研究的数据来源于BERKELEY EARTH数据库(Data Overview-Berkeley Earth),选取1972年11月至2023年10月全球陆地月平均气温异常及1880年~2022年全球年平均气温作为样本数据。
2.2. 数据预处理
在进行气温数据信息采集工作时,可能会受到意外因素影响,使得某些数据偏离真实值,出现异常的谷峰波动,这样的数据点被称为异常点,如果不加以适当的修正,将会影响模型对气温变化规律的学习。因此,本文采用
准则如式(1)
(1)
对数据集进行异常值处理,满足
准则的值占总样本点的1%以内可判断其为异常值,并用相邻两个数据的均值进行填充。
为了解决数据集过大而导致模型运行耗时以及不同类别气象要素量纲不同对模型训练的影响,我们采用了数据标准化处理,以统一要素指标之间的量级关系。标准化也称为归一化,通常情况下,归一化后数据范围在[0, 1]以及[−1, 1]之间。本文中,我们将数据统一归一化到[0, 1]范围内。其计算公式如式(2)所示。
(2)
式中,
和
分别为归一化前后的值,
为各特征样本数据的极小值,
为各特征样本数据的极大值。
3. 全球气温异常分析
3.1. 描述性分析
首先,对预处理后的全球陆地月平均气温异常数据进行描述性分析。图1为近50年全球陆地月气温异常图,可以看出,在全球陆地范围内,月平均气温异常呈现逐年递增趋势。但气温异常接近长期趋势线,初步判断没有出现异常增长。为进一步判断近10年间气温上升与过去任意10年间的气温增长是否存在显著差异性,还需进行差异性分析。
3.2. 差异性分析
差异性分析是常用的数据分析方法,用于检测科学实验中实验组与对照组差异的方法,又称差异性显著检验。差异性分析是假设检验的一种,判断样本间差异主要是随机误差造成的,还是本质不同。

Figure 1. In the past 50 years, the global average monthly land temperature has been abnormal
图1. 近50年全球陆地月平均气温异常
差异性分析通常有三种:ANOVA,T-test,Chi-Square Analysis。本文采用ANOVA检验近10年与过去任意10年间的气温增长是否存在显著差异性。
将样本数据分为实验组和对照组,具体划分原则如表1所示。
方差分析结果如表2所示,p值为0.000小于0.05拒绝原假设,表示各组之间气温增长没有显著性差异,即近10年没有出现气温异常增长。
4. 气温预测模型的构建与对比分析
本节选取百分之九十的气温序列数据作为模型训练集,剩余百分之十为模型测试集。对训练集和测试集数据进行数据预处理得到有效数据,再作为模型输入。
4.1. 基于ARIMA模型的气温预测
4.1.1. 平稳性检验
将2012~2022年的全球平均气温数据作为验证集,1880~2011年的全球平稳气温作为训练集进行模型拟合,拟合的时间序列图如图2。

Figure 2. Temporal diagram of global steady temperature from 1880 to 2011
图2. 1880~2011年全球平稳气温时序图
从图2可以看出,该时序图是非平稳的,总体呈现上升趋势。因此,在进行模型拟合前,需要对数据进行差分处理,一阶差分处理结果如图3。
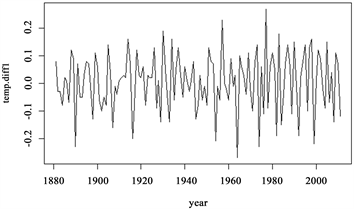
Figure 3. First-order difference diagrams
图3. 一阶差分图
从差分图可以直观的看出一阶差分是平稳序列,并且采用ADF单位根检验得到p-value = 0.01,则可以说明一阶差分后的序列是平稳的。
4.1.2. 模型识别和参数估计
由于数据是一阶差分平稳,我们的模型识别主要集中在一阶差分序列的识别、拟合和预测上。为了确定ARMA模型的p和q阶数,我们通过分析差分序列的ACF和PACF图来进行。图4和图5展示了ACF和PACF图的程序运行结果。
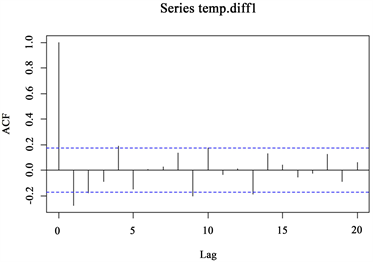
Figure 4. ACF plot after first-order difference
图4. 一阶差分后ACF图
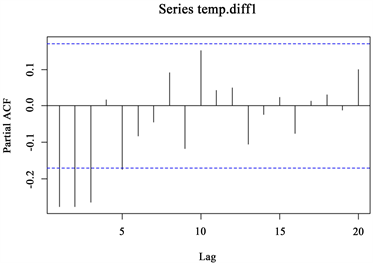
Figure 5. PACF plot after first-order difference
图5. 一阶差分后PACF图
通过观察自相关图和偏自相关图,再经过模型检验,我们最终确定的一阶差分模型为ARIMA(3, 1, 5)模型。
根据程序的最终估计结果,一阶差分后模型的各项系数见表3:

Table 3. ARIMA(3, 1, 5) coefficient table
表3. ARIMA(3, 1, 5)各项系数表
得到的方程式为:
(3)
4.1.3. 模型预测及分析
预测结果见表4:

Table 4. ARIMA model prediction results data table
表4. ARIMA模型预测结果数据表
预测图见图6,预测值和真实值对比见图7。

Figure 6. Forecast map of global average annual temperatures
图6. 全球年平均气温预测图
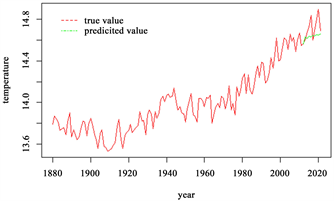
Figure 7. Global annual average temperature ARIMA model forecast and true value overall comparison chart
图7. 全球年平均气温ARIMA模型预测和真实值整体对比图
从表4中可以看出,预测值和真实值之间的误差较小。然而,通过观察图7可以发现,预测值和真实值之间的趋势存在明显差异。这主要是因为时间序列分析在长期预测中存在一定的收敛性,导致预测值的波动相对平稳,从而使得趋势不够明显。
4.2. 基于CNN-LSTM模型的气温预测
将1880年至2022年的全球年平均气温数据,共计143个样本点,经过预处理后以9:1的比例划分为训练集和测试集,将1880年至2007年的128个气温数据当作训练集,2008年至2022年的15个气温数据作为测试集。
首先,我们对预处理后的数据进行了描述性分析,图8展示了1880年至2022年全球年平均气温的变化趋势。可以看出,全球年平均气温呈现出逐年递增的趋势,变化较为平稳。在没有气温突变的情况下,不同年份的气温变化趋势具有类似的规律。

Figure 8. Trends in global annual mean temperature from 1880 to 2022
图8. 1880年至2022年全球年平均气温的变化趋势
在CNN-LSTM模型的训练过程中,随着迭代次数的增加,误差反向传播并不断更新参数。在初始阶段,MAE的下降速度较快。然而,当迭代次数达到300次后,MAE的下降速度开始减缓,模型逐渐趋于稳定,学习速率开始降低。最终,平均绝对误差收敛至1.5左右,表明模型预测的准确性已达到一个较为理想的状态,如图9所示:

Figure 9. Variation curve of loss function in CNN-LSTM model
图9. CNN-LSTM模型损失函数变异曲线
2008年至2022年CNN-LSTM模型的气温观测数据和预测数据的曲线对比图如图10所示,我们可以观察到气温预测数据和实际观测数据曲线基本重合,没有出现滞后的位移偏差,由此可以说明CNN-LSTM模型对气温的预测具有较高的准确性,预测效果优良。
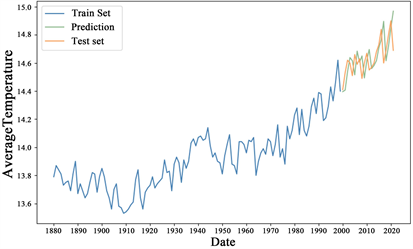
Figure 10. Comparison of temperature observation data and forecast data curves of CNN-LSTM model from 2008 to 2022
图10. 2008年至2022年的CNN-LSTM模型气温观测数据和预测数据曲线对比图
用训练好的CNN-LSTM模型预测未来20年全球年平均气温,结果如表5所示。

Table 5. Global average annual temperature forecast for the next 20 years (˚C)
表5. 未来20年全球年平均气温预测(℃)
4.3. 模型对比
4.3.1. 模型评价指标
为了对模型预测结果进行客观评估,本文选用了三个评价指标来评估全球气温数据的预测结果,这三个指标分别是:绝对误差(MAE)、平均绝对百分比误差(MAPE)和均方根误差(RMSE)。通过这三个指标的综合考量,可以全面评估模型预测的准确性和可靠性,这些指标的具体表达式如下:
(4)
(5)
(6)
式中:
为气温预测值;
为气温真实值;
为预测点个数。
4.3.2. 结果分析
ARIMA模型与CNN-LSTM模型的评价指标对比见表6。

Table 6. Comparison table of the evaluation indicators of the two models
表6. 两种模型评价指标对比表
由表6可以看出两种预测模型都比较好,但结合ARIMA模型的预测图(见图7)和CNN-LSTM模型的预测图(见图10),CNN-LSTM模型预测的效果更优于ARIMA模型,预测结果更加准确。
5. 总结与建议
本文采用CNN-LSTM模型对全球气温进行了预测研究。通过对历史气温数据的分析,我们发现该模型能够有效地捕捉气温变化的长期趋势和季节性规律,从而提高了预测精度。与传统的ARIMA模型相比,CNN-LSTM模型在预测精度和稳定性方面表现更优。通过对比预测值与观测值曲线图,我们发现气温预测数据与实际观测数据曲线基本重合,进一步证明了CNN-LSTM模型在气温预测方面的有效性。CNN-LSTM模型能够有效地提高气温预测精度,为应对全球气候变化问题提供有力支持。未来,我们可以通过进一步优化模型参数和完善数据预处理方法,进一步提高模型的预测性能。同时,还可以将该模型应用于其他气候相关领域,为气候变化研究提供更多有价值的信息。
基金项目
重庆市教委科技项目–科学技术研究项目(青年) (KJQN202101129)和2023年重庆理工大学研究生教育高质量发展行动计划资助成果(gzlcx20233309)。
NOTES
*通讯作者。