1. 引言
随着能源紧缺和环境污染问题的日益严重，燃料电池作为一种清洁、高效的能源转换装置 [1] ，正越来越受到人们的关注。其中，燃料电池端板作为支撑和固定电池单体的关键部件，其结构性能对整个燃料电池系统的运行稳定性具有重要影响。为了提高燃料电池的性能和降低成本，开展燃料电池端板结构的优化设计具有重要意义 [2] 。对于本文涉及到的大型燃料电池堆，在封装过程中需要使用端板、螺栓等部件对整体组件进行紧固，因此端板是燃料电池组件中必不可少的部分。
人们已经开展了很多端板的改进研究，比如改变端板形状，在端板表面加筋或改变接触面形状。另外，Yu等 [3] 也通过设计端板内侧接触面预变形的方法，使端板在封装载荷的作用下达到近似平面的状态。有专利中提供了一种封装薄壳装置，装配于端板和螺栓头之间，该装置中心区域向端板内凹并与之接触，装置的外边缘在施加封装力前与端板留有平行的间隙，在封装过程中可以通过改善端板的弯曲变形达到改善内部压力均匀性的目的。Wang等 [4] 通过结合液压袋，设计了一种增压端板，对内部接触压力均匀性有一定的改善。Yu等 [5] 提出一种含有预变形的绝缘泡沫芯端板，他在设计中考虑了端板的轻量化的需求，这种端板不仅有保温减重的效果，还对内部压力的均匀性有一定的改善。Lin [6] 通过多目标拓扑优化的方法，以端板最大刚度和内部压力最均匀性为设计目标，改善了端板结构，在保证了端板刚度的同时，改善了电堆内部压力，对端板的减重也有一定的效果。拓扑优化不同与结构优化和尺寸优化，是一种对结构的材料分布的优化设计方法，可作为后续优化的基础。相对于传统的端板结构设计，端板的拓扑优化采用理论工具指导材料的最优分布，给出端板结构设计的概念雏形，加快了优化设计进程。
在现有技术条件下，要想使新能源汽车续航能力更加持久，就要降低整车质量，而对于大型电堆，端板质量占整体质量很大一部分，因此设计电堆端板结构形状时，需要在保证端板强度可靠性和功能要求的情况下通过优化结构设计极可能地减小其质量，达到轻量化的目标 [7] 。
2. 三燃料电池三维模型建立
2.1. 模型建立
本文通过SOLIDWORKS进行三维建模，根据燃料电池的实际尺寸和材料属性，如表1所示。对燃料电池的各个部件进行精细的三维建模，如图1所示。首先，建立了燃料电池的单电池结构模型，包括端板、绝缘板、集电板、膜电极、气体扩散层、催化剂层等部件。
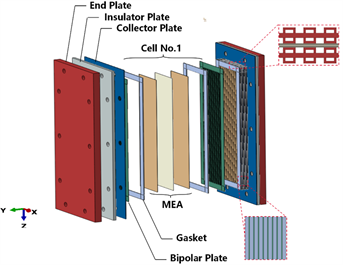
Figure 1. Schematic diagram of fuel cell structure
图1. 燃料电池结构示意图
2.2. 有限元模型建立
Figure 2. Fuel cell finite element model
图2. 燃料电池有限元模型
本文研究的质子交换膜燃料电池堆是由许多零部件相互接触组成的，考虑到完整模型结构十分复杂，因此在综合电堆性能和结构方面，对电堆进行结构简化。如图2所示。
3. 端板拓扑优化
3.1. 拓扑优化方法
在解决实际问题时，我们经常会遇到需要同时考虑多个目标函数的情况，这就是所谓的多目标优化问题。多目标优化问题并不是要求所有的目标都达到最优解，而是通过协调和平衡各个目标函数，使得各个目标函数都能达到相对最优解。
对于多目标优化问题，常用的求解方法有两种。一种是加权系数法，该方法是将多个目标函数分开求解，然后将各单目标函数进行耦合求解。另一种是多目标优化算法，该方法是通过得到所有权重组合的最优方案来求解多目标优化问题。
在本章中，我们将采用双目标拓扑优化的方法对燃料电池端板结构进行优化设计。具体而言，我们需要在保证端板强度与刚度的同时，实现端板的减重，并尽可能使电堆内部应力分布均匀。为了实现这个目标，我们将采用加权系数法进行求解。
需要注意的是，在Optistruct中并不能直接实现这两个优化目标，需要进行一定的转化。具体而言，我们将端板刚度最大化转化为端板应变能最小化，将电堆内部接触压力分布最均匀化转化为对应区域节点位移均方根最小化。这样，我们的目标函数就可以写成：
(1)
(2)
(3)
其中ω1 = ω2 = 0.5，f = 0.3。
在求解这个目标函数时，我们需要考虑一些约束条件。这些约束条件包括：端板的几何形状和尺寸约束、材料性能约束以及接触压力分布的约束。我们将采用加权系数法进行求解，具体步骤如下：
1) 首先，利用单目标拓扑优化方法，分别求解两个单目标优化问题，得到两个最优解；
2) 然后，将两个最优解进行组合，得到一个新的最优解；
3) 重复步骤1和步骤2，直到得到一个满意的解。
需要注意的是，加权系数的选取对于优化结果的影响较大。不同的加权系数可能会导致不同的优化结果。因此，在实际应用中，需要根据具体问题进行合理的调整。
3.2. 优化结果
为了研究拓扑优化对电堆端板减重和改善电堆内部接触压力均匀性的效果，我们对原始电堆的进气端板进行了初步的拓扑优化设计。在图3中展示了进气端板拓扑优化基础模型，其中设计区域尺寸为325 mm、136 mm、40 mm，并避开了气体通道和端板四周螺栓的位置。端板整体厚度为60 mm，为了减少人为设置的干扰，在端板的底部留出20 mm的非设计厚度。
在优化设计之前，我们需要在Hypermesh软件中导入模型组件并定义相关参数，以及建立各部件之间的接触关系。完成前置工作后，进行网格划分，然后可以施加所需的荷载及位移边界条件。参考实际工程情况，给定电堆封装载荷为42 kN，并均匀施加在14根螺栓上，以模拟封装效果。
拓扑优化结果中的变量主要是单元的相对密度。相对密度值越大，表示材料在该单元分布越密集。对于变密度法，端板上相对密度的变化是连续的。为了能够找到合适的设计结构，在显示密度云图时通常需要设置一个显示阈值。通过将小于这个阈值的单元隐藏，可以突出显示优化后得到的拓扑结构。
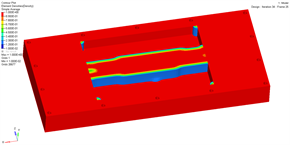
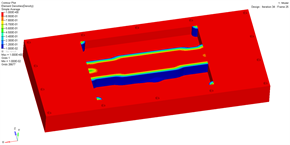(a) 阈值0.1 (b) 阈值0.2
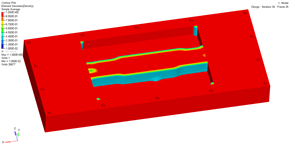(c) 阈值0.3 (d) 阈值0.4
Figure 4. Results of dual-objective optimization under different density thresholds
图4. 不同密度阈值下双目标优化结果
图4展示了进气端板在不同密度阈值下的双目标优化结果。可以看出，材料主要集中在设计区域的中部，连接两边的螺栓孔，呈现出中心对称的分布趋势。这种分布趋势可以减少进气端板的应变能并提高其刚度。同时，将材料分布集中在端板的中间区域，也可以提高端板的局部刚度，减轻其在受到螺栓封装力时的弯曲变形。随着密度阈值的增加，拓扑结构上材料分布逐渐减少。选取密度阈值为0.4时的优化结构作为拓扑优化后的端板结构，并对其进行处理以进行静力分析。需要注意的是，拓扑优化得到的优化结构不考虑外观尺寸，只是为结构设计提供材料分布的参考。
观察重建端板的弯曲变形情况和应力分布情况，并与原始端板进行比较。图5展示了原始端板及优化后端板的位移变形图，其中变形放大倍数为50倍。可以看出，原始端板两端的弯曲变形相对于优化后的端板更大一些。
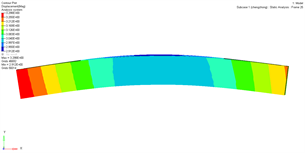
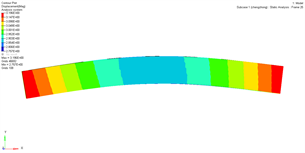(a) 原始端板 (b) 优化后的端板
Figure 5. Optimization of front and rear end plate deformation
图5. 优化前后端板变形
4. 结语
在本文中，我们研究了燃料电池电堆的进气端板，通过优化设计来达到轻量化和刚度提升的目标。我们首先对进气端板进行了拓扑优化，通过改变单元的相对密度来重新分布材料。在优化过程中，我们采用了双目标优化方法，考虑了端板的刚度和质量两个目标。
通过对比不同密度阈值下的优化结果，我们发现随着密度阈值的增加，拓扑结构上材料分布逐渐减少，而相对密度的变化也呈现出类似的趋势。我们选取了密度阈值为0.4时的优化结构作为最终的端板设计，这种设计在保证刚度的同时，实现了35.15%的减重效果。
为了评估优化后端板的性能，我们对其进行了静力分析，并比较了原始端板和优化后端板的位移变形情况。结果显示，优化后的端板在保证刚度的同时，降低了弯曲变形量。此外，我们还对内部接触压力的均匀性进行了评估，发现优化后模型内部接触压力均匀性提高了10.28%。
总之，本文通过对进气端板进行优化设计，实现了显著的轻量化效果，同时保证了刚度和内部接触压力均匀性。这些改进对于提高燃料电池电堆的性能和可靠性具有重要意义。我们的研究结果为燃料电池系统的优化设计提供了有益的参考。未来，我们将进一步研究其他部件的优化设计方法，以实现整个燃料电池系统的轻量化和性能提升。