外立面突出构件对高层建筑风荷载特性影响研究

Study on the Influence of Facade Protruding Members on Wind Load Characteristics of High-Rise Buildings

摘要: 为研究方形高层建筑表面外立面突出构件对高层建筑风荷载的影响，通过在光滑表面分别贴11种不同形式突出构件的方法改变建筑表面外立面突出构件，进行方形高层建筑模型测压试验，得到各工况下层风力系数，进而分析了矩形格栅工况下层风力功率谱和相关性的影响。研究表明：三种模型表面的布置均会增大建筑脉动阻力系数，矩形格栅和水平板的布置会略微增大平均阻力系数，竖向板和矩形格栅的布置都会减小脉动升力系数，增幅随测点层高度的下降而增大。表面布有矩形格栅板会降低建筑物横风向脉动风荷载，但宽度越大，降低效果越不明显，甚至当宽度增大到一定程度时，会增大建筑物横风向脉动风荷载。矩形格栅框基本上既不会改变横风向脉动层风力功率谱也不会改变层风力相关性，只有增加矩形格栅框厚度时会略微改变。总的来说，方形建筑表面布置合理尺寸的水平板、竖向板、矩形格栅有利于气动优化。

Abstract: To study the effect of protruding components on the wind load of square high-rise buildings, 11 different forms of protruding components were pasted on smooth surfaces to change the protruding components on the building surface. A square high-rise building model pressure test was conducted to obtain the wind force coefficients of the lower layer under each working condition, and then the influence of the wind power spectrum and correlation of the lower layer under the rectangular grid working condition was analyzed. Research has shown that the arrangement of the three model surfaces will increase the building’s pulsation resistance coefficient, while the arrangement of rectangular grids and horizontal plates will slightly increase the average resistance coefficient. The arrangement of vertical plates and rectangular grids will reduce the pulsation lift coefficient, and the increase will increase with the decrease of the measurement point layer height. The presence of rectangular grid panels on the surface can reduce the crosswind pulsating wind load on buildings, but the wider the width, the less significant the reduction effect. Even when the width increases to a certain extent, it will increase the crosswind pulsating wind load on buildings. The rectangular grid frame basically does not change the crosswind fluctuation layer wind power spectrum or the layer wind correlation, only slightly changes when the thickness of the rectangular grid frame is increased. Overall, the rational arrangement of horizontal and vertical panels, as well as rectangular grilles on the surface of square buildings, is beneficial for aerodynamic optimization.

1. 引言

建筑外立面会根据需求附着不同的突出构件或不同的覆面材料，呈现出多样化。建筑外表面的复杂装饰条、阳台和幕墙格栅等突出构件等会导致建筑表面突出构件有很大的不同，对建筑结构的风荷载产生一定的影响。

Stathopoulos等 [1] 研究发现，增大建筑表面粗糙度会减小迎风面上部和侧风面的局部风压。Mruta等 [2] 研究表明，风压受到表面粗糙度的影响显著，特别是在侧壁前缘附近，增加表面粗糙度会减弱气流的分离，抑制漩涡脱落。黄冬梅等 [3] 通过风洞试验研究发现，粗糙条对顺风向气动力功率谱的影响较小，表面粗糙化可以减小一部分区域的风荷载和风振响应。Yuan等 [4] 、Hui等 [5] 和杨易等 [6] 通过风洞试验研究了水平隔板对方形高层建筑风荷载的影响，发现不同布置的水平隔板能大幅度减小侧风面的风压，尤其是负极值风压，同时对横风向层风力有一定的影响。刘子荷等 [7] 和Quan等 [8] 研究了竖向肋板对方形高层建筑气动力特性的影响，发现竖向肋板能显著降低横风向脉动层风力和基底弯矩。柯延宇等 [9] 研究了竖向肋条对高层建筑局部覆面风压的影响，发现增加肋条的布置会增大侧风面肋条分界线的前缘区域平均风压、脉动风压和极值风压。程旭等 [10] 研究了粗糙条围护结构对高层建筑风荷载的影响，发现水平粗糙条对建筑表面风压均值和脉动值影响较小，有使其分布趋于均匀的作用，伸出长度越大，极值吸力减小也越明显；竖向粗糙条导致了明显更大的风压梯度，伸出长度越大，极值吸力增大也越明显，最大增大可达到25.8%。艾辉林等 [11] [12] 通过CFD获取了不同风向角下外围装饰条上的风荷载数值和风荷载体型系数分布规律。Zheng等 [13] [14] 通过CFD研究了阳台对表面风压系数的影响，研究发现阳台会增大迎风面平均风压系数。

综上所述，目前学者关于竖向板和水平板对高层建筑风荷载影响的研究，已取得了一定的进展，但较少考虑建筑外立面为矩形格栅的情况。本文用ABS板制作的水平板、竖向板、矩形格栅框来模拟高层建筑外立面突出构件，改变其宽度和厚度，进行了刚性模型同步测压风洞试验，分析了不同立面附件对方形高层建筑整体风荷载的影响。

2. 试验概括

2.1. 试验风场模拟

试验在湖南科技大学大气边界层风洞中完成，风洞试验段尺寸为4 m × 3 m × 1 m (宽 × 高 × 长)，试验段空风洞风速最大可达30 m/s。通过在风洞中布置尖劈装置和粗糙元调试出缩尺比为1:400的C类风场，风洞试验布置如图1所示。参考高度取模型高度H，即0.6 m (对应实际高度240 m)，参考高度处来流的平均风速即参考风速UH约为10.3 m/s，风场参数如图2所示，其中U_z为z高度处平均风速。

Figure 1. Wind tunnel setup and test model

图1. 风洞布置与试验模型

(a) 平均风速与湍流强度(b) 脉动风速谱

Figure 2. Wind tunnel setup and test model

图2. 风场特性

2.2. 试验模型

选取实际高度240 m且表面无附件的方形截面高层建筑作为基准建筑，建筑横截面边长为48 m。试验模型几何缩尺比为1:400，由ABS塑料板制作，试验模型高H = 600 mm，横截面边长B = 120 mm。风洞阻塞比为0.6%，其影响可以忽略不计。本实验共设有11种附属构件分别布置在基准模型表面，其中模型A1、A1-I和A1-II表面布置横向板，模型B1、B1-I和B1-II表面布置竖向板，模型C1、C2、C3、C3-I和C3-II表面布置矩形格栅框，所有附件布置均不采用封角设计，布置如图3所示。图4为附属构件几何参数，11种附属构件参数如表1所示：表中br = b/B，dr = d/B，hr = h/H，ar = a/B。

参考模型REF 模型A1 模型A2 模型C1 模型C2 模型C3

Figure 3. Part of the model 3D diagram

图3. 部分模型三维图

Table 1. Parameters of rectangular grating

表1. 几何参数

Figure 4. Geometric parameter

图4. 几何参数

2.3. 测点布置及量测

试验模型表面测压点布置和试验风向角如图5所示，采样频率为333 Hz，采样时长为60 s，采样长度为20000个数据。为确保试验的准确性，在每个矩形框中均布有测点。由于模型为正方形具有双轴对称性，风洞试验风向角为0˚~90˚，间隔为10˚，并增设了45˚的风向角试验。

3. 层风力系数

3.1. 水平板和竖向板

试验模型层风力由各层测点同步测压试验结果积分获得，层风力系数按下列公式计算：

$C_D\left(z\right)=\frac{\overline{F_D\left(z\right)}}{A\left(z\right)q_r}$

${C^{\prime }}_D\left(z\right)=\frac{{\sigma }_D\left(z\right)}{A\left(z\right)q_r}$

${C^{\prime }}_L\left(z\right)=\frac{{\sigma }_L\left(z\right)}{A\left(z\right)q_r}$

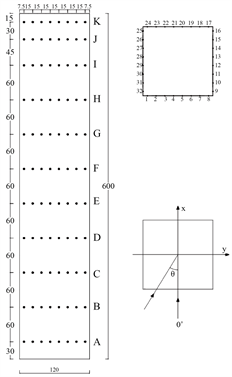
Figure 5. Part of the model 3D diagram

图5. 测点布置及风向定义

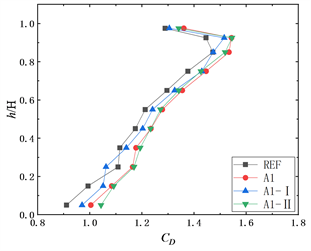
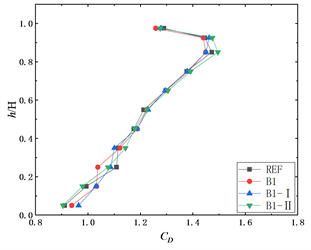
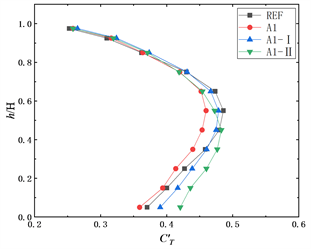
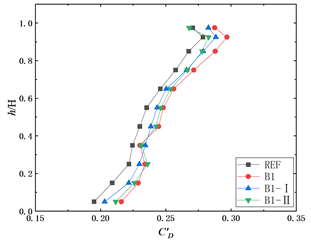
其中， $C_D\left(z\right)$ 、 ${C^{\prime }}_D\left(z\right)$ 、 ${C^{\prime }}_L\left(z\right)$ 分别为z高度处的层平均阻力系数、层脉动阻力系数和层脉动升力系数； $\overline{F_D\left(z\right)}$ 、 ${\sigma }_D\left(z\right)$ 、 ${\sigma }_L\left(z\right)$ 分别为z高度处层平均阻力、层脉动阻力和层脉动升力。 $A\left(z\right)$ 为z高度处受风面积； $q_r$ 为参考来流风速压。图6展示了在0˚风向角下参考模型REF、模型A1、A1-I、A1-II、B1、B1-I、B1-II、C1、C2、C3、C3-I和C3-II的层风力系数沿高度变化的情况。

图6(a)~(c)分别为参考模型REF和表面布置了水平板模型的平均阻力系数、脉动阻力系数和层脉动升力系数。从图6(a)可以看出，参考模型REF的平均阻力系数最大值出现在0.85H高度处，数值约为1.47。而模型A1、A1-I、A1-II的最大值出现在0.93H高度处，数值上相较于参考模型略有增大。总体上来看，

(a) 平均阻力系数 (b) 脉动阻力系数

(c) 脉动升力系数 (d) 平均阻力系数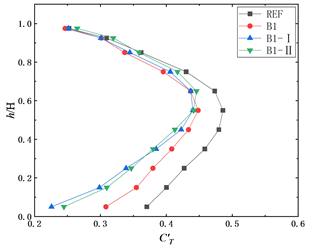(e) 脉动阻力系数 (f) 脉动升力系数

Figure 6. Wind layer force coefficients

图6. 层风力系数

表面布置水平板会略微增大建筑的平均阻力系数。从图6(b)可以看出，参考模型REF、模型A1、A1-I、A1-II的层脉动阻力系数最大值均出现在0.93H高度处，布置了水平板的模型脉动阻力系数最大值略大于参考模型。值得注意的是，dr = 3.3%的水平板模型的层脉动阻力系数模型大于参考模型。从图6(c)可以看出，水平板对脉动升力系数影响较小。

图6(d)~(f)分别为参考模型REF和表面布置了水平板模型的平均阻力系数、脉动阻力系数和层脉动升力系数。从图6(d)可以看出，布置竖向板的模型的平均阻力系数最大值和参考模型一样在0.85H高度处，数值变化较小。总体上来看，竖向板的布置对平均阻力系数没有明显的影响。从图6(d)可以看出，参考模型REF、模型B1、B1-I、B1-II的层脉动阻力系数最大值均出现在0.93H高度处，数值上布置了水平板的模型均大于参考模型。相较于参考模型，表面布置水平板会增大建筑的脉动阻力系数，平均增幅分别为6%、4%、4%。从图6(f)可以看出，相比参考模型REF，表面布置竖向板会减小脉动升力系数且减幅会随着建筑高度的降低而增大。对比B1、B1-I和B1-II的脉动升力系数发现，增大竖向板的宽度和厚度均会略微增大脉动升力系数。

3.2. 矩形格栅

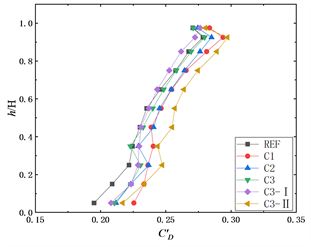
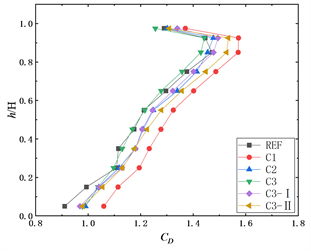
从图7(a)可以看出五种表面布置了矩形格栅的模型的平均阻力系数在模型底部较小，随着模型高度的增加平均阻力系数逐渐增加，变化趋势和参考模型REF一样，其最大值均出现在距底部0.93H高度处，数值上均比参考模型大。总体上来看，模型C3的平均阻力系数和参考模型差别不大，当增加br (模型C1)后会明显增大模型的平均阻力系数，相较于参考模型平均增幅约为10%。当增加矩形格栅板宽度(模型C3-I)，平均阻力系数都有一定程度的增加，其中模型B2的最大平均阻力系数分别为1.49，相较于参考模型增长量为1.4%。对比模型C3-I和B2-II可以发现，增加矩形格栅框的厚度会略微增大平均阻力系数。

(a) 平均阻力系数 (b) 脉动阻力系数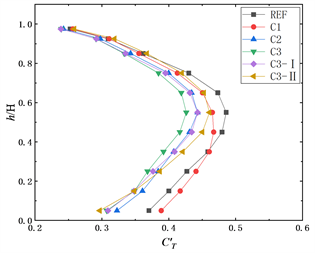(c) 脉动升力系数

Figure 7. Wind layer force coefficients

图7. 层风力系数

图7(b)和图7(c)分别为五种表面布置了矩形格栅的模型的脉动阻力系数、脉动升力系数随高度的变化曲线。从图7(b)可以看出，模型C3-II的脉动阻力系数相较于参考模型有略微的增大，平均增幅为5%。由图7(c)可见，表面布置网格格栅模型的横风向脉动层力系数的变化趋势和参考模型REF的变化趋势一样，都是随模型高度增加而增大，在模型0.55H高度处达到最大值，然后又随着高度的增加而减小。和竖向板对脉动升力系数影响一样，矩形格栅会减小脉动升力系数且减幅会随着建筑高度的降低而增大，其中模型C3的减幅最为明显，当br = 23% (模型C1)相较于br = 11% (模型C3)，脉动升力系数会明显增大，是因为竖向板数量变少，使得抑制作用减弱。

4. 层风力概率谱

从层风力系数可知矩形格栅框对高层建筑整体风荷载较为明显，图8给出了0˚风向角下0.55H高度处的脉动风力功率谱分布，进一步阐述了矩形格栅框对层风力脉动特性的影响。图中f为频率， $f_B/U_H$ 为折减频率， $S_D\left(f\right)$ 、 ${\sigma }_D^2$ 分别为顺风向脉动层风力的功率谱密度和方差。 $S_L\left(f\right)$ 、 ${\sigma }_L^2$ 分别为横风向脉动层风力的功率谱密度和方差。

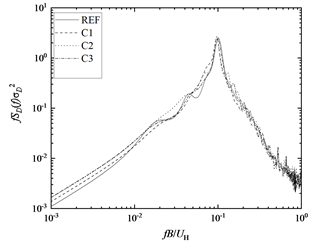
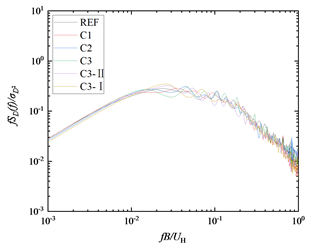(a) 顺风向(b) 横风向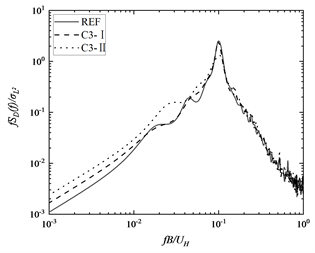(c) 横风向

Figure 8. Power spectra of fluctuating wind layer force

图8. 层脉动风力功率谱

从图8(a)中可以看出，参考模型REF和布置了矩形格栅框的五种模型的顺风向脉动层风力功率谱分布规律基本一致，能量均分布于较宽的频带内。图8(b)是取参考模型REF和dr = 2 mm工况的模型的横风向脉动层风力的功率谱，从图中可以看出，当建筑表面布置dr = 2 mm的矩形格栅框时，既不会改变横风向脉动层风力功率谱的峰值和峰值出现的折减频率，同时增大矩形数量和格栅条的宽度都不会改变横风向脉动层风力功率谱的峰值和峰值出现的折减频率。这是因为装配了厚度为2 mm的网格格栅框的模型截面仍然是正方形，和参考模型REF一致，就不会改变方型模型表面的漩涡脱落频率。模型表面布置横向肋条能够略微增大功率谱峰值处的能量 [4] ，模型表面布置竖向肋条能够略微减小功率谱峰值处的能量 [7] ，因为矩形格栅框是横竖交叉的肋条框，所以在建筑表面布置矩形格栅框不会改变横风向脉动层风力功率谱的峰值。从图8(c)中可以看出，模型C3-II的功率谱峰值小于模型C3-I，模型C3-II的功率谱峰值出现的折减频率大于模型C3-I，这是因为增大矩形格栅框的厚度，使横风向升力频域特性发生改变，漩涡脱落的频率会有所增大，同时气流在侧风面的漩涡脱落被抑制，从而方向建筑横风向功率谱峰值。

5. 层风力相关性

任意两层的层脉动风力相关性的计算公式为：

$C_{ij}=\frac{{\sigma }_{ij}}{{\sigma }_i{\sigma }_j}$

式中， ${\sigma }_{ij}$ 为i、j两层的脉动层风力的协方差； ${\sigma }_i$ 和 ${\sigma }_j$ 分别为i、j两层的脉动层风力的根方差。图9为层间脉动风力的相关系数随层间距离的变化规律。这里选取0.55H高度处的层风力作为参考层风力，分别求出0.55H高度层风力与其余各层层风力的相关系数。从图9中可以看出脉动风力的相关系数均随层间距的增大而减小，在模型表面布置矩形格栅框对相关性影响较小，当增大格栅框的厚度会略微减小0.55H高度层风力与下半部分各层层风力的竖向相关性。结果表明，矩形格栅对脉动风力功率谱影响较小。

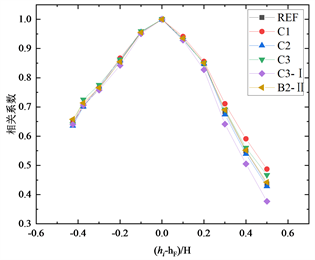
Figure 9. Power spectra of fluctuating wind layer force

图9. 层脉动风力功率谱

6. 结论

本文通过风洞试验研究了用水平板、竖向板和矩形格栅改变方形建筑外立面突出构件的方法对高层建筑风荷载的影响，得到以下结论：

1) 水平板会略微增大高层建筑的平均阻力系数和脉动阻力系数，dr越大增幅越大。竖向板的布置会略微增大脉动阻力系数，同时会减小脉动升力系数且减幅会随着测点层高度的降低而增大。

2) 表面布置网格格栅会增大0.25H高度以下的平均阻力系数，0.65H高度以上的平均阻力系数随着格栅单元面积、宽度和厚度的增加而增大。所有布置矩形格栅模型在距模型底部0.45H高度以下区域的顺风向脉动层风力系数均比参考模型大，模型A1、B2-II、B3的增幅相对较为显著。模型B1对降低横风向脉动层风力的效果最好，最大降幅出现在距模型底部0.05H高度处，为17%，表面布有矩形格栅板会降低建筑物横风向脉动风荷载，但宽度越大效果越不明显，甚至当宽度增大到一定程度时，会增大建筑物横风向脉动风荷载。

3) 当建筑表面布置dr = 2 mm的矩形格栅框时，不会改变横风向脉动层风力功率谱的峰值和峰值出现的折减频率。同时增大矩形数量和格栅条的宽度都不会改变横风向脉动层风力功率谱的峰值和峰值出现的折减频率。但增大矩形格栅框的厚度会使功率谱峰值出现的折减频率减小，同时会增大功率谱的峰值。

致谢

能够顺利完成本次实验，要感谢李永贵导师的悉心指导，师姐师兄的教诲，同门师弟的帮助。

参考文献