1. 引言
锂离子电池(LIBs)以其高能量密度、长循环寿命和较低的自放电能力等特性成为电动汽车动力源的首选。 [1] 为了增加电动汽车续航里程,锂离子电池在不断追求高能量密度和高成组效率,单体电池正在向大型化方向发展 [2] 。大尺寸电池由于其结构的特殊性,其电热特性在空间上差异尤为突出。此外,为了追求更高的成组效率,电池组内部的温度分布不均匀现象更加严重 [3] 。考虑到成本和系统复杂性,温度传感器通常布置在汇流排、端盖和电池表面三个位置。然而,有限数量的温度传感器很难准确监测到电池或电池组的温度分布和最高温度点,这对电池的热安全构成了较大的风险。为了预防热安全事故的发生,电池热管理系统(BTMS)必须根据实时的温度场及时调整控制策略。要实现有效的BTMS,必须准确预测电池和电池组的温度分布。利用热模型获得温度分布已被证明是一种有效的方法 [4] 。因此,人们对电池热模型进行了广泛的研究,以获得准确的电池温度分布,以改善电池的热平衡 [5] 。
在过去的LIBs在线温度估计研究中,虽然取得了很多突破,但仍然存在一些局限性。例如,过去的研究工作主要集中在小型电池上 [6] ,且多数没有考虑极柱区域产热对电池温度分布的影响,也没有考虑电池本体的非均匀生热特性 [7] 。为了更好地描述大尺寸电池的温度分布,本文提出了一种基于卡尔曼滤波算法的大尺寸电池温度估计方法,以解决计算效率和计算精度之间的矛盾。
2. 实验
2.1. 实验对象
本文选择研究对象为150 Ah磷酸铁锂刀片电池,其参数如表1所示。
2.2. 模型参数测试
模型参数的精度直接影响电池热模型的精确度,一些文献报道中模型参数是参考文献中的数值,然而不同类型电池之间的参数具有较大差异性,势必会影响模型的计算精度。为了提高模型精度,采用实验测量的方式确定模型参数 [8] 。
2.2.1. 脉冲内阻测试
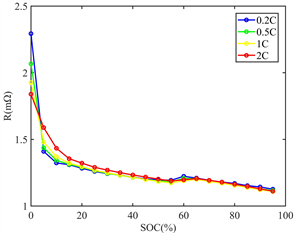
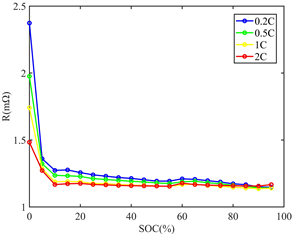
电池内阻是电池热模型的重要参数,电池内阻一般分为欧姆内阻和极化内阻。本文采用HPPC (The Hybrid Pulse Power Characterization)方法测试电池的脉冲内阻。HPPC方法是采用阶跃电流对电池进行充放电,记录电池的电压的变化,根据电流的幅值和电压的响应计算电池的脉冲内阻。通常情况下,欧姆内阻用1秒的直流内阻来表示,电池总内阻由10秒内阻来表示。测量结果如图1所示。
 (a) (b)
(a) (b)
Figure 1. Resistances of the battery: (a) Charging; (b) Discharge
图1. 电池内阻:(a) 充电;(b) 放电
2.2.2. 熵系数测试
电位法通过预定义的SOC测量点的OCV与环境温度之间的线性关系的斜率来确定熵热系数。我们先对电池进行CC-CV充满至100% SOC。在25℃下静置1小时后,通过温度梯度实验确定电池熵热系数。环境温度经过7种温度(45℃、35℃、25℃、15℃、5℃、0℃、−10℃)最终冷却到−20℃。电池在每个温度下静置3个小时,并记录不同温度下的端电压。然后将环境温度调节到25℃两小时,然后放电10% SOC调节到下一个测试点。
恒温箱最后时刻的端电压作为当前温度下的OCV。不同的环境温度与相关OCV呈高度线性关系,其斜率为当前SOC点的熵热系数。在图2中给出了整个SOC范围内的熵热系数。
2.2.3. 比热容测试
为了获得电池的比热容,进行了比热容实验。在两块电池中间布置恒定功率的加热片,并使用隔热棉将电池外部包裹起来。在大尺寸刀片电池上等距选取三个测温点1、2、3。分别在加热片表面和两块电池外表面对应的测温点位置贴上热电偶测量温度。在营造的绝热环境下,近似认为加热片的发热量被电池全部吸收而使得电池温度提高。公式(1)可用于计算电池的比热容。取三个测点计算结果的平均值作为电池的比热容。
(1)
其中Cp、Pheat、M和dT/dt分别为电池的比热容、加热片的加热功率、两块电池的总质量和电池的温升速率。
最终测得刀片电池比热容为1139.7 J/(Kg·K)。
2.2.4. 导热系数测试
导热系数通过实验和模型辨识相结合得到。在两块电池的中心布置了一块薄膜加热片,并在加热片表面涂抹少量导热硅脂,以确保加热片与两块电池之间有良好的热接触。假设加热片能够均匀加热两块电池。在两块电池的外侧等距各布置5个热电偶,其中测点1位于电池大面中心位置。使用隔热棉对电池进行包裹,以达到近似绝热的效果。通过加热片加热上下两块电池,并记录温度数据。同一测点测量的两个温度数据做平均值处理,作为该测点的温度值。应用COMSOL Multiphysics建立符合导热系数测试过程的物理模型,并取三个测点的温度值,作为参数模型辨识的目标温度。
通过优化仿真温度曲线可以得到辨识结果:电池厚度方向导热系数λz = 1.07 W/(m∙K)、电池展向导热系数λx = λy = 20.95 W/(m∙K)。
3. 温度估计方法
3.1. 区域划分
本文根据刀片电池的内部结构,将刀片电池整体分为5个区域。图3为对刀片电池整体进行的整体划分以及实验传感器的布置位置。
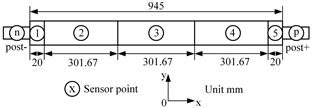
Figure 3. Regional division and sensor placements
图3. 区域划分和传感器位置
3.2. 电池产热建模
3.2.1. 极耳产热的建模
由于极柱区域的产热率远大于电池本体的产热率,并且极柱区域的面积很小,因此可以认为极柱区域的温度在每个位置都是相等的 [9] 。然后,可以将极柱区域与电池本体相连的地方作为第一类边界条件,极柱区域作为电池本体区域的外部传热节点。根据能量守恒定律,可以通过使用集总参数法来构建极柱区域的热模型,如下所示:
(2)
其中Ts是极柱温度;ms和Cp,s分别是极柱的质量和比热容;Qs是极柱区域的产热率;Rh,s是极柱区域在环境温度下由对流换热产生的热阻;Tamb为环境温度;n和p分别代表负极和正极;Qs,k是从极柱传递到电池本体区域的传热率,其中与负极极柱连接的是电池本体区域1,与正极极柱连接的是电池本体区域5 (即1与n连接;5与p连接)。
3.2.2. 电池本体温度分布的建模
为了降低电池几何结构的复杂性,提出了一下假设:1) 将电池核心视为具有各向异性导热系数的均质立方体。2) 为了降低计算成本,忽略电池的产热不均匀性,因此仅根据每个节点所含电芯体积将发热量分配到每个节点 [10] 。3) 假设热参数(包括导热系数和比热容)与温度无关。4) 电池内部的对流传热和所有辐射传热均被忽略。
电池本体产热主要包括四个方面:不可逆热、可逆热、混合热和副反应热 [11] 。传统的锂电池产热模型忽略了电池的化学反应热和混合热,只考虑不可逆热,即电池内阻产生的焦耳热和极化反应产生的极化热,以及熵变产生的可逆热。电池的产热模型表示如下:
(3)
其中Qirrev和Qrev分别表示不可逆热和可逆热项,总产热量是两项之和。
每个产热项可以表示如下:
(4)
其中I是充放电电流;E是电池的端电压;Uocv是电池的开路电压;R是电池的脉冲内阻;T是电池的温度;dUocv/dT是电池的熵热系数。
本文将刀片电池本体热模型简化为五个节点的一维热模型,节点数的选择兼顾了精度和计算速度。五个节点的能量传递可以根据传热学理论中的热平衡方程来描述:
(5)
大尺寸刀片电池在在宽度和厚度方向上的尺寸较小,整个电池的温差主要体现在长度方向上。因此,在瞬态模型中可以合理的忽略厚度方向和宽度方向上的热传递。热平衡方程可以简化为:
(6)
其中ρk是节点区域的密度;Cp,k是节点区域的比热容;Vk是节点区域的体积;λx、λy和λz分别表示刀片电池x、y和z方向上的导热系数。
除此之外还应考虑电池的散热。对于大尺寸刀片电池与环境的对流换热,传热规律满足第三类边界条件,可以表示为:
(7)
其中,Rh,k是节点区域在环境温度下由对流换热产生的热阻。
将三维热模型简化为一维热模型,即热流沿着一个方向流动 [12] 。每个节点被表示为一个热源,并且热模型的五个节点温度被近似地描述为五个区域的体积平均温度。两个节点之间的距离是节点区域长度和的一半,即步长。用微分法求解能量传递的热平衡方程,可以表示为:
(8)
在公式的右边,第一项Qheat,k为产热率,第二项和第三项为相邻节点区域之间的传热,第四项为节点区域的散热。Ck表示节点区域的等效热容,Rx,k,k+1表示节点k和节点k + 1之间传热的热阻。
将公式中的微分方程离散化,其中时间步长设置为1s,节点的温度可以由等式表示。其中Bt、Ct和At是系数矩阵。Qheat,t为产热率矩阵。Tt为在t时刻的温度矩阵,Tt+1为在t + 1时刻的温度矩阵,可根据公式对任意时刻的Tk,t+1进行求值。
(9)
3.3. 基于卡尔曼滤波算法的温度计算
卡尔曼滤波(Kalman filtering,简称KF)算法是由Rudolf E. Kalman在1960年提出的一种利用线性离散系统的状态空间方程,由系统的输入、输出数据,在已知系统噪声的统计特性的基础上,对系统的状态量进行最优估计的方法。
卡尔曼滤波作为现代控制理论的重要组成部分,在表达上采用系统状态空间描述的方法,在算法迭代上采用递推的形式。
设线性离散系统的状态空间方程的表达式为:
(10)
其中,xk表示系统第k时刻的状态量;yk为系统第k时刻的观测量;A、B、C、D分别为系统的系数矩阵;wk−1为系统的过程噪声;vk为系统的测量噪声。
KF算法的五步递推公式为:
(11)
KF算法的五步递推公式中,卡尔曼增益Kk是观测量yk在修正后验状态估计值时所占的权重。当状态量的初值与真值相比偏差较大时,先验估计误差协方差矩阵Pk变大,卡尔曼增益Kk变大,观测量yk在修正状态量估计值时所占的权重变大,使状态量估计值趋近于真实值;随着状态量的估计值与真值相比偏差逐渐变小,先验估计误差协方差矩阵Pk变小,卡尔曼增益Kk变小,观测量yk在修正状态量估计值时所占的权重减小,状态量的估计值逐渐收敛于真值。因此,当系统状态量的初值选取与真值相比存在较大误差时,经过KF算法的迭代和修正,系统状态量的估计值将会收敛于真值。
将传感器3测量的温度作为实测温度,利用卡尔曼滤波算法进行闭环校正。刀片电池中间三节点可以用状态空间方程表示:
(12)
根据状态空间方程,可以得到采用KF算法进行温度估计的状态向量xk、系统输出量yk和输入量uk,从而可列系数矩阵A、B、H的具体表达形式,具体方程如下式所示:
(13)
(14)
(15)
(16)
(17)
(18)
4. 仿真结果
本文的算法仿真在MATLAB & Simulink平台展开,基于KF算法对刀片电池的温度进行在线估计。为了验证提出的非均匀产热的简化多节点热模型在不同工况下的估计精度,在恒温箱内进行了恒流放电测试和动态工况测试,并对仿真结果和试验结果的温度变化趋势进行了对比分析。
图4为2C恒流放电工况下电池各个区域实验温度和仿真结果的对比。可以看出在最大温升的工况下,电池五个区域的模拟绝对误差均小于1.88℃,可见模型的准确性。
为了进一步验证所提出的热模型在驾驶条件下的估计能力,进行了动态工况实验。动态应力测试(DST)、新欧洲汽车法规循环工况(NEDC)和城市道路循环(UDDS)在许多研究中被用来评价锂电池的性能。本文设计了一种包含了这三种测试的混合动态工况来验证模型的准确性。在图5(a)上显示了不同区域的实验和预测的比较结果。由于动态工况下的产热相对较小,温度随电流的变化不明显,最大温升不足7℃。计算结果与实测数据吻合较好,证明该方法在动态工况下也能很好的预测温度变化,所提出的热模型可以捕捉电池中关键的动态热力学变化。
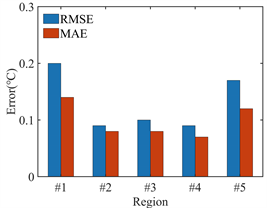
此外,在动态工况下计算出不同区域温度的RMSE和MAE结果在图5(b)中。模型MAE和RMSE的最大值均在区域#1位置处。MAE最大值为0.1424℃,RMSE最大值为0.2022℃。这表明在动态工况下,所提出热模型可以很好地描述锂电池在动态工况下的热响应。
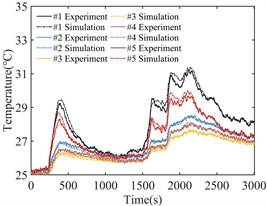 (a) (b)
(a) (b)
Figure 5. Hybrid dynamic condition: (a) Estimation temperature; (b) Estimation error
图5. 动态工况:(a) 温度预测;(b) 预测误差
5. 结论
本文提出了一种基于卡尔曼滤波算法的温度估计方法用于大尺寸刀片电池的温度分布预测,主要结论如下:
1) 该方法充分考虑了电池极耳产热对电池温度分布的影响。通过将电池划分为多个区域,考虑极耳产热对电池温度的影响,可以提高估计的精度。
2) 通过简化电池本体的传热节点,来提高模型的计算速度。结果表明,该模型可以在1 s内计算出大尺寸刀片电池的温度分布,且精度较高。
3) 在不同测试工况下的温度实时误差均小于1.88℃,RMSE在1.35℃以内,MAE在1.18℃以内。
未来的努力将集中在将该温度估计方法扩展到具有复杂边界条件的电池组之中,并最终将其集成到现有的BTMS之中。
基金项目
国家自然科学基金面上项目(52277222);上海市自然科学基金项目(22ZR1444500)。