1. 引言
随着新课程改革的不断深入,数学教育的目标不仅仅是求解数学问题,还应该注重培养学生的逻辑思维、创新能力,以帮助中学生塑造正确的世界观、人生观和价值观。但根据目前的中学数学教育情况,数学课程思政教育略显不足。随着教育改革的不断深入,越来越多的教育工作者认识到,在数学课程中融入思政教育是提升学生综合素质的必要手段。因此就需要创生与中学数学课程教学相匹配的课程思政教育,使学科知识的学习与德育教育相结合。
2. 课程创生概述
学者李小红对“教师的课程创生”进行了界定,认为教师课程创生是指教师根据本校的实际情况、自身的知识经验和能力优势、学生的兴趣爱好和发展水平,在整个课程运作过程(包括课程开发、课程实施、课程评价等)中通过批判反思来实现对课程目标、课程内容(包括文本内容和非文本内容)、课程资源、课程意义和课程理论的持续的主动建构 [1] 。
课程创生的目的是提高学生学习的效果和效率,培养学生能够适应未来社会需要的能力和素质,使课程教学更加适应现代化的教学需求。课程创生不仅仅是课程内容和教学方法的创新,还包括对教材的研发和编写、师资培训、教育评估等全方位的改革。课程创生“以人为本”的教育理念,强调学生的自主学习和实践操作能力,具有较强的前瞻性和创造性,能对未来教育的发展产生积极影响。
3. 数学课程创生的案例
函数是中学数学的重要内容之一,其教学的难点是使学生理解函数抽象的概念,在教学中体现函数的本质属性。那么如何将复杂的函数概念课中融入课程思政元素,让学生更好地理解和应用函数的概念,同时培养学生的创新能力和实际应用能力,提升学生的整体素质和思政教育效果呢?
教学设计:
[教师先板书:从一穷二白到世界第二,彰显了中国在经济、科技和文化等领域巨大的进步。]
(一) 复习回顾,搭建桥梁
1) 在一个过程中,固定不变的量称为常量,可以取不同数值的量称为变量 [2] 。如,购买课本时,课本的单价称为常量,购买的数量和对应的总价是变量。
2) 表示变量之间的关系的方法有:解析法、列表法、图像法。
函数是刻画变量之间关系的常用模型,什么是函数?我们一起去探究。
(二) 实践探究,交流新知
篇章一:富起来
【探究1】下表是我国近几年的国内生产总值(GDP)的统计表
根据表1内容,回答问题

Table 1. Statistical table of gross domestic product (GDP)
表1. 国内生产总值(GDP)的统计表
1) 在这个问题中有几个变量?分别是什么?
答:两个变量,分别是年份x,国内生产总值y。
2) 对于给定的年份x,相应的国内生产总值y确定吗?
答:对于给定的年份x,相应的国内生产总值y随之确定。
篇章二:快起来
【探究2】2018年6月中国新版高铁“复兴号”率先在北京发车,如图1是“复兴号”高铁从某车站出发,在行驶过程中速度v (单位:千米/分钟)与时间t (单位:分钟)的关系。
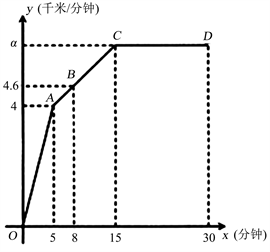
Figure 1. Driving speed and time diagram
图1. 行驶速度与时间关系图
1) 在这个变化中,有几个变量?自变量,因变量是什么?根据上图填表2。

Table 2. Driving speed and time relationship
表2. 行驶速度与时间关系表
2) 对于自变量的每一个值,因变量有几个值与之对应?
答:唯一一个。
篇章三:强起来
【探究3】2022年10月中国宇航员在太空直播了一场科学课,引发了学生了解科学知识的新热潮。植物生长研究社团通过查阅资料得知一种树苗栽种时的高度约为80厘米,生长过程中,树苗的高度h (单位:厘米)与载种以后得年数n满足的关系式如下:h = 80 + 25n
1) 在这个问题中,有几个变量,分别是什么?
答:两个变量;树苗的高度h和栽种后的年数n。
2) 当x分别等于1,5,10时,相应的树苗高度是多少?
答:105厘米,205厘米,330厘米。
3) 给定一个大于0的n值,你能求出相应的h吗?
答:能。
【议一议】问题1:在上面3个问题中,存在着哪些共同点?
知识要点1:函数的定义。
【议一议】问题2:在上面3个问题中,存在着哪些不同点?
知识要点2:函数常用的三种表示方法:a) 解析法;b) 列表法;c) 图像法
【议一议】问题3:在上面3个问题中,自变量能取哪些值?
知识要点3:函数值的一一对应关系。
(三) 巩固学习,应用知识
1) 浙江某市苹果的价格是10元/千克。设用购买苹果x千克时,应付金额为y元,则y关于x的函数解析式为_____________,当x = 5时,函数值为________,它的实际意义是________________________________。
2) 国内某快递寄件价格如下表3。

Table 3. Price list for express delivery items
表3. 快递寄件价格表
a) b是a的函数吗?说明理由。
b) 分别求当a = 2,4,8时的函数值,并说明它的实际意义。
(四) 课堂小结
师:通过这节课我们有什么收获?
学生活动:先独立思考,再举手回答。
师:本节课我们通过富起来,快起来,强起来的探索过程,学习了函数的定义、表示方法以及函数值的概念;并能感受到数学来源于生活实际。
师:希望通过本节课的学习,同学们能够有所启发,有所感悟,有所收获。白日不到处,青春恰自来,苔花如米,小也学牡丹开,山河虽无恙,吾辈当自强,愿同学们以青春之小我努力学习,发奋图强,为大国之崛起贡献自己的力量。
4. 课程思政面临的问题
融入课程思政的数学教学设计通过中国经济富起来、中国速度快起来、中国科技强起来三个篇章进行展开,激发学生的爱国之情和强烈的民族自豪感,激发了学生的学习斗志,为中国的崛起而读书的理想信念。从而使本节课的“情感、态度与价值观”目标得到了升华,实现了融入思政教育的数学课程的创生。
数学课程承载着知识教育和价值教育的双重属性。传统意义上讲,数学课程目标围绕知识传授和能力培养,思政目标存在“浅表化”“硬融入”等问题。数学落实课程思政,要树立融合思维,让教学目标的思政价值凸显起来,育人功能强大起来 [3] 。下面就数学课程思政教学的主要问题展开讨论和探讨。
第一,课程思政内容浅显。课程思政内容必须与课程内容紧密结合,将国情、民族团结等相关内容有机地融入数学教学中。但有些思政教育,在加入课程内容方面经常出现抽象简单、缺乏针对性的现象,这会引发学生对思政教育的反感与不感兴趣。因此,在课程思政教育设计过程中,必须要确立好教学目标,具体化教学内容,真正做到思政教育与课程的链接紧密,并且要提倡真材实料的教学方法,注重符合学生心理的思政教育手段。
第二,传统教学模式的限制。传统教育模式教师通常采用基础的教育手段,而缺乏动态交互的互动式教学方式。这样的教学方式缺乏趣味性,学生学习效果与学习兴趣受到影响。因此,需要学校与教师积极创生新型教学模式,选择合适的教学手段和辅助教学工具,例如利用数字化平台、在线辅导、互动配合等方法,增加教学内容的多样性和趣味性。
第三,教学方式单一。数学课程思政教学方式缺乏互动和参与性,往往只是单向传授知识,容易导致学生长时间的被动学习感到厌烦。为了启发学生的思考和激发学习兴趣必须采用互动式教学方式,让学生主动参与其中,例如以竞赛的形式进行教学,活跃课堂气氛来激发学生学习兴趣,通过实际操作掌握更有深度的知识和技能,提高教学质量。
5. 总结与展望
数学课程与思想政治教育的融合是当今教育体制下亟待解决的问题。在教学实践中,面临着许多挑战和困难,包括教学内容的设计、授课形式的创新、技术手段的应用等方面。为了更好推进数学课程的创新与思想政治教育的强化,我们积极的进行数学课程创生。
首先,教学内容的设计要体现思想政治教育的要求。数学作为一门学科,其教学内容应与思政教育紧密结合,将国情、国家政策、社会问题等有机融入数学教学中。通过引入与实际生活相关的数学问题和案例,让学生在数学学习中感受到思想政治教育的影响和引导。例如,可以通过在数学问题中涉及社会公平、公共利益等话题,培养学生的社会责任感和公民意识。
其次,授课形式应注重互动和参与。传统的数学教学往往是教师单向传授知识,学生被动接受。为了激发学生的学习兴趣思考能力,教师应采用多样的教学方法和策略,营造活跃的课堂氛围。例如,可以采用小组讨论、问题解决、角色扮演等互动式教学,让学生积极参与到数学学习和思想政治教育中去。同时,教师还应给予学生充分的发言权和表达自己观点的机会,关注他们的思考过程和个人成长。
技术手段的应用可以提升教学效果。在信息技术高度发达的今天,教育技术已成为推动教育改革的重要引擎。在数学课程思想政治教育中,教师可以利用多媒体教学、在线教学平台等技术手段,创造丰富多样的教学资源和环境。例如,通过使用电子白板或教学软件进行演示,可以更直观地呈现数学问题和思想政治内容,提高学生的学习效果。同时,通过在线平台和移动学习等方式,可以推广可融合的数学课程和思想政治教育内容,使更多的学生受益于现代化教育手段。
此外,教师的专业素养和教学指导也至关重要。教师应不断提升自身的学科知识水平,以及思想政治教育的理论素养。同时,学校和教育部门应关注教师的专业发展和培训,提供有针对性的教学指导。只有教师具备更好的教学能力和方法,才能创生出更好的数学课程,真正提高数学课程思想政治教育的质量,为学生的成长提供更加积极的引导。
总而言之,数学课程与思想政治教育的融合是当今教育发展的重要任务。我们必须加强教学内容的创生,注重授课形式的创生,将技术手段应用于教学实践,并提升教师的专业能力和指导水平。只有通过综合性的探究和努力,才能真正促进数学课程思想政治教育的深入发展,引导学生成为具有真正受教育的人。
NOTES
*第一作者。