基于Plant Simulation的混合流水线作业序列优化

Optimization of Hybrid Assembly Line Job Sequencing Based on Plant Simulation

摘要: 为了完成某公司的智能制造转型计划，对该公司车间的生产流程、生产布局以及产品的生产工艺进行了调研，根据该车间的生产特点，将其归类为混合流水线车间调度(HFSP)这一典型的NP-hard问题。以最短作业时间(SPT)调度为优化目标，使用遗传算法去解决这一问题。具体方法上使用Plant Sim-ulation仿真软件，结合现场生产实际情况，搭建起车间流水线生产模型，应用遗传算法实现最优排序，得到近似最优解。经过遗传算法计算后的生产作业序列，理论上按此指导进行生产，总的作业时间可以缩短15%左右，从而提高企业生产效率；另外，厂家只需要导入即将执行的产品数量及工艺信息到模型，经过模型计算即可获得推荐排序。因此，此方式具有一定的实际应用价值和指导意义。

Abstract: In order to complete the intelligent manufacturing transformation plan of a company, the production process, production layout and product production process of the company’s workshop were investigated. According to the production characteristics of the workshop, it was classified as a typ-ical NP-hard problem of hybrid flow shop scheduling (HFSP). The shortest operation time (SPT) scheduling is taken as the optimization goal, and genetic algorithm is used to solve this problem. In the specific method, Plant Simulation software was used to build the production model of the workshop assembly line combined with the actual situation of the field production, and the genetic algorithm was used to achieve the optimal sequencing, and the approximate optimal solution was obtained. After the genetic algorithm calculation of the production sequence, theoretically according to this guidance for production, the total operation time can be shortened by about 15%, so as to improve the production efficiency of enterprises; In addition, the manufacturer only needs to import the product quantity and process information to be executed into the model, and the recommended ranking can be obtained after the model calculation. Therefore, this method has certain practical application value and guiding significance.

1. 引言

随着经济市场的发展，制造业产品市场朝着多品种、小批量、个性化的方向发展；这种现象一方面导致新产品的需求量激增，另一方面促使现有的车间生产方式进行优化提升，以满足市场对产品的需求。因此对于车间装配水平的提升，值得企业进一步研究。车间作业排序问题被广泛认为是一项具有挑战性的NP难题，也被归类为最复杂的组合优化问题之一。尽管在这一领域的研究已取得了一些实际应用成果，但由于问题的高度复杂性，存在一些难以克服的弱点，例如处理大规模问题变得几乎不可能，同时全局最优解的获得也异常困难。

这个问题的复杂性涵盖了主要两个方面的变化，即不同产品加工顺序所引发的不同加工时间和生产平衡率的多变性。随着问题规模的扩大，计算复杂度呈指数级增长，传统的分析方法往往难以胜任，或者只能满足局部的优化条件，远远达不到预期。目前较好地满足需求的方法主要是利用工业仿真软件搭建仿真模型，使用功能组件对数据进行优化。该方法包括在仿真软件中构建模型，随后使用仿真语言编写程序，以通过仿真优化获得最佳的车间作业排序。通过将算法语言直接嵌入仿真过程中，可以直观地观察到最佳制造顺序，以实现最小化最大完工时间、加快在制品周转率等目标。

近年来，学者对于车间混合流水线生产的研究不断深入，一部分学者使用仿真软件对该问题进行探索，另外一部分学者是通过结合实际问题改造相关算法来解决这类情况。王晓峰等 [1] 运用FCFS规则，形成解决混合调度流水线问题的改进遗传算法，并利用仿真软件建立混合流水线调度运行的仿真模型，验证改进遗传算法求得的解。周金平 [2] 根据车间装配线的特点，使用仿真软件搭建流水线模型，对一整个配送系统的数据流进行统计优化。如卜康正等 [3] 基于NSGA2遗传算法并设定多个优化目标；从而得到Pareto解，结合实际问题从Pareto解集中得到最优方案。张海涛等 [4] [5] 以工件最短生产周期为优化目标，通过MATLAB等仿真软件优化出静态调度问题解最优值与最优调度方案，从而给出最佳调度策略。肖福龙 [6] 梳理出产线生产的流程工艺，生产布局以及存在的生产不平衡之处，使用仿真软件找出其生产瓶颈，对生产线进行平衡优化。王静云 [7] 针对多目标不相关并行机混合流水车间调度问题，建立以最小化最大完工时间、机器总能耗和机器加工成本为目标的多目标数学模型，提出一种改进的基于分解的多目标进化算法。程廷等 [8] [9] [10] 采取多目标优化算法，对遗传算法的编码解码、种群初始化以及局部搜索方面进行了优化,改进的调度算法使得迭代次数降低、可跳出局部最优、获得的解的质量也更高。M. EBRAHIMI [11] 提出了两种元启发式算法，即非支配排序遗传算法(NSGAII)和多目标遗传算法(MOGA)，并在不同维度上对两种算法的定量和定性结果进行了比较。

本文使用Plant Simulation这一仿真平台，针对当前流水线半流程半离散的机械生产特点，搭建起车间运行仿真模型；使用遗传算法结合最短作业时间这一优化目标，进行仿真优化。最后，导入工厂真实工单信息数据以及产品工艺信息到仿真平台上，验证该优化方法的有效性。

2. 问题描述

车间作业排序问题描述

当前车间作业排序问题可描述为：有j个工件，它们需要经过i个工序进行加工，每道工序需要在对应加工工位上完成，每道序的加工时间是已知的。

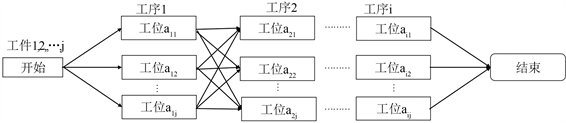
Figure 1. Workpiece processing flow chart

图1. 工件加工流程图

如图1所示，当前混合流水线车间调度的约束如下：

1) 同一时间每台设备只能加工一道工序，且每道工序只能被一台设备所加工，同时加工过程不可间断，整个过程中设备均处于有效工作状态。

2) 整个加工过程中，每个工件不能在同一台设备上加工多次。

3) 工件必须按照工艺路线以指定的次序在设备上加工，工件n的第i道工序必须在其前一道工序完成后才能开始。

4) 考虑工件之间的加工优先权，允许操作等待。

5) 工件的工时事先给定，且在整个加工过程中按设定好的分布函数上下波动。

6) 同工件的工序之间没有优先约束关系。

总的来说，产线推荐作业排序就是安排等候某个设备或工作中心加工的多个任务，确定这些任务加工的先后次序，使预定的目标最优化。实际上就是要解决如何按时间的先后，将有限的人力、物力资源分配给不同工作任务，使预定目标最优化的问题。这个预定的目标可以是产线完工时间，也可以是生产产品的成本。

3. 遗传算法

可供车间作业序列优化的算法有很多，比如遗传算法，模拟退火算法，蚁群算法等等。本文采用遗传算法来解决这一问题，遗传算法优化的终极目的是确定一个作业序列，即将工件的每个工序合理分配到对应设备的某个时间段，使得当天作业的最大完工时间最小。

3.1. 染色体编码

车间调度问题有多种染色体编码方式，此次研究采用基于工序的编码方式。结合当前车间作业调度问题描述，对于N个产品M台机器的车间作业调度问题而言，染色体编码为： $\left[r_1,r_2,r_k,\cdots ,r_{N\ast M}\right]$ ，其中 $r_k$ 为工件号，此工件号在染色体中第n次出现，表示执行该工件的第n次工序。在每条染色体中，有N × M个基因。对于单生产线多产品调度而言， $r_k$ 表示第k个操作的产品号。这样的编码方式可以保证随机产生的调度方法的可行性。

Table 1. Information map of workpiece processing

表1. 工件加工信息图

以表1中3台机器、3个工件的调度问题编码为例：一次完整的调度有3 × 3道工序，每条染色体包含3 × 3个基因。可假设随机初始化染色体为：[1 2 3 1 1 2 2 3 3]。其中，1表示工件J₁，2表示工件J₂，3表示工件J₃，因为每个工件有3道工序，所以,每个工件在一个染色体中刚好出现3次。在染色体[1 2 3 1 1 2 2 3 3]中，出现3个2表示工件J₂的3道工序，第1个2对应工J₂件的第1道工序在设备2上加工，第2个2对应工件J₂的第2道工序在设备3上加工，第3个2对应工件J₂的第3道工序在设备1上加工。可见，工件的所有工序都用相同的符号2命名，并且根据它出现的染色体中的顺序得到解释。将染色体解释为可行的作业排序，如图2所示：

Figure 2. Diagram of theprocess coding

图2. 工序编码图

可见，设备1上工件的加工顺序为1-2-3；设备2上工件的加工顺序为2-3-1；设备3上工件的加工顺序为1-2-3。

3.2. 适应度函数

如何使适应度函数与优化目标相一致是保证遗传算法有效优化作业序列的关键，对于HFSP问题，本文选取的优化目标为最大完工时间的最小值，所以可以采用整个任务的最小完工时间的倒数作为优化目标。所以有，一定数量的工件经过工艺路线所规定的工序加工，其中染色体 $gen\left\{i\right\}$ 在每道工序上花费的时间为 $F_{\max }={\max }_{1\le i\le n}\left\{F_i\right\}$ ，所以适应度函数可以表示为：

$\text{fitvalue}=\frac{1}{F_{\max }}$ (1)

3.3. 选择算子

选择算子有多种方式，比如二进制锦标赛、线性排序、指数排序等，本文采用轮盘赌选择的方法。轮盘赌选择又称比例选择方法，其基本思想是：种群中的个体被选中的概率与个体相应的适应度函数的值成正比。将种群中所有个体的适应度值进行累加然后归一化，最终通过随机数对随机数落在的区域对应的个体进行选取，类似赌场里面的旋转的轮盘。即值越大，越有可能被选中遗传到下一代，则染色体i被选中的概率为：

$p_i=\frac{F_i}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{F}_i}}$ (2)

3.4. 交叉算子

本文采取了工序编码方式，为了防止产生非法解或者基因冲突的现象，我们可以采用部分映射交叉(Partially Mapping Crossover, PMX)、次序交叉(OrderCrossover, OX)等方式来设计交叉算子。本文选用部分映射交叉方式PMX。具体步骤描述为：采用随机规律来生成两个交叉点，两个染色体在此基础上进行交换基因的操作。交换基因之后，若交叉点内外的基因编码不发生冲突，则保留此次交换结果。如果基因编码发生冲突，则在基因片段中寻找可以替换的基因编码，进而产生新的染色体。PMX具体过程如图3所示：

Figure 3. Diagram of the partially mapping crossover principle

图3. 部分映射交叉原理图

3.5. 变异算子

由于本文采取了工序编码的方式，所以基因突变可以采取互联变异和逆转变异两种方式。互联变异是指在染色体片段中选取两个基因点，交换其位置形成新的染色体。如个体[1，2，3，4，5，6，7，8，9]，随机选择3、6，交换后的个体为[1，2，6，4，5，3，7，8，9]。而逆转变异是指在染色体中截取一个片段，对此基因段进行逆转从而形成新的个体。如个体[1，2，3，4，5，6，7，8，9]，随机选择3、6，逆转后的个体为[1，2，3，6，5，4，7，8，9]。本文选择互联变异方式。

4. 模型设计与结果分析

4.1. 仿真软件介绍

Plant Simulation是一款西门子旗下的工业仿真软件，用户可以仿真和优化生产物流系统和工艺。Plant Simulation可以对各种规模的工厂和生产线，进行建模、仿真和优化生产系统，分析和优化生产布局、资源利用率、产能和效率、物流和供需链等。它是面向对象的、图形化的、集成的建模、仿真工具；系统结构和实施都满足面向对象的要求。

4.2. 实验设计

4.2.1. 实验数据

在本案例中，选取由8台设备 $\left(M_1,M_2,\cdots ,M_8\right)$ 加工9个工件 $\left(J_1,J_2,\cdots ,J_9\right)$ ，工件对应的工序加工时间如表2所示。对工时数据和工艺流程进行整理后，本文针对装配车间的加工流程进行生产逻辑编程。结合Plant Simulation的基本组件特性，本文使用缓存区模仿实际生产过程中的加工等待过程；该厂房产品的加工步骤可基本概括为：压装机压装–手工辅助工序–气密机检测–检验包装；对于其半流程半离散的加工特点，可以针对工位工时做区间化处理；以及各个产品的加工流向，使用程序实现根据工艺路线自动路由。

Table 2. The schedule of work piece corresponds to the process

表2. 工件对应工序时间表(单位：S)

4.2.2. 实验设计思路和结果

首先是针对工时区间的设置，做了一些处理。在实际生产过程中，工人对每个产品的作业时间是在一定区间随机波动的，采用区间数表征工时的不确定性，通过将给定的工时数据进行区间化，获取区间加工时间，使仿真更真实。采用了模糊化方法对已知确定条件下一些算例的加工数据进行区间化，对每个工件每道工序的加工时间进行区间化。现给定确定的加工时间t，对其进行区间化后所得到的区间加工时间为[a × t, b × t]，这里a < 1，b > 1，两个因子分别取值a = 0.85，b = 1.3。

在分析工具中输入当前产线要做的每个产品的名称、工艺路线、各个工序的标准工时以及初定前后作业顺序；设定好产品与产品更替生产之间，生产线的停滞时间；经过plant模型的计算，得到当前生产线的最优生产序列，具体代码逻辑设计见图4所示。

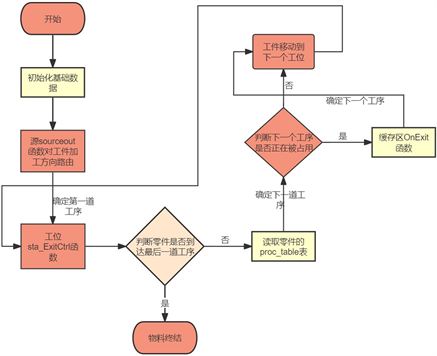
Figure 4. Diagram of the industrial simulation model logic

图4. 工业仿真模型逻辑图

针对车间流水线装配制造的特点，使用工业仿真软件模拟整个车间生产流程，搭建起仿真模型，如下图5所示。该流水线模型囊括三大模块，其中模块一中的sourceout方法控制每个工件的起始加工工位，sta_ExitCtrl方法控制工件在工位之间的流转逻辑。模块二为承担不同种类加工任务的工位以及缓存区等基本组件，模块三为信息导入导出以及优化进度控制模块。

首先，模块三可以实现订单信息的导入与删除，增强了数据的拓展性。其次，模块二中设定的工位以及缓存区，可以视为这个流水线模型的字典数据，设定好这些基本数据之后；模型才能较好地模拟出真实生产流程。最后由模块一中的路由程序以及控制逻辑，推动所有在制品进行物流移动。由此，本文可以得出较为准确的工件加工总耗时，以及使用遗传算法工具对其进行优化。

Figure 5. Diagram of the pipeline model

图5. 流水线模型图

模块一中的GA插件为该仿真软件的遗传算法优化工具，在该模块中设定好种群的大小以及规模，并设置适应值按fitness函数方法计算。通过多次迭代，模拟出工单在不同工件加工优先顺序下，所耗费的最大作业时间。得到优化结果之后，通过仿真，对比优化前后完成工单所需时间，即可得出结论。具体结果如下图6所示：

Figure 6. Performance chart

图6. 性能图

从图6 (横坐标代表迭代次数，纵坐标代表适应度函数值)可得出结论，随着迭代次数的递增，运算结果趋于一个稳定的水平；红线代表每次迭代计算中的最优排程方案，蓝线代表最差排程方案，绿线介于二者之间。以优化最短作业时间为目标的适应度函数值在第8代种群之后收敛到最佳状态，从而我们可以得到最合适的排序结果。此时工件的推荐加工优先级为8-5-1-3-2-4-7-9-6，此时适应度值为13 min。

5. 结语

本文提出一种仿真优化方法，调研某企业车间作业调度现状，并在此基础之上搭建Plant Simulation模型；对遗传算法进行针对性改造，比较好地解决了当前流水线车间调度问题。通过实时导入企业实际生产工单信息以及相应的产品工艺数据，可以生成最优生产序列，使生产排程达到设备级，对于提升企业的装配制造水平具有一定的指导意义。但由于现实流水线生产中会有紧急插单或者设备故障等不确定情况，要想更贴切车间实际生产情况，仍然需要进一步完善模型，纳入其他可优化的参数，解决生产调度多目标优化的问题。