1. 引言
生产系统在运行过程中,受多种因素的影响难免会发生退化,这将导致系统运行异常,从而降低系统的运行效益。在明确退化规律的基础上,对系统的运行状态进行检测,并采取相应的维修方案是常用的应对手段之一。Luis等 [1] 通过对伽马过程的参数结构进行调整以模拟退化的变化规律。Franck等 [2] 基于伽马退化过程,提出一种完美的纠正措施和不完美的预防措施的状态维修策略。Zhang等 [3] 提出一种结合状态检查和不完美制造过程的综合经济模型,以确定最佳的生产批量和预防性维修阈值。Khatab等 [4] 建立了一个确定最优检测周期和退化阈值水平的集成优化模型。Zheng等 [5] 基于状态检测结果制定不同的维修方案,通过最小化平均成本率来优化生产批量和视情维修策略。在生产系统的运行状态难以直观判定时,可以借用验收抽样的思想,通过检验产品质量推断系统的运行状况。Abdessamad等 [6] 将检验策略建立在动态抽样计划的基础上,根据退化情况调整抽样间隔,并考虑了生产、维修和质量控制之间的相互关系。Wu [7] 利用可变样本量的方法检测系统的运行状态,以单位时间平均运行成本最小为目标,选择最优检测策略。Bose等 [8] 利用在线抽样检验方法对生产系统的状态进行判定,并讨论了生产批量的决策问题。Liu等 [9] 基于部分可观察马尔可夫过程,构建了多类型检验和在线检验模型,使单位时间内的长期平均成本最小。在维修方案优化设计方面,Wang等 [10] 根据退化程度对系统状态进行评估,提出了一种基于状态的预防性维护策略。Ahmad等 [11] 考虑了部件质量问题、检查错误、维修成本和系统可用性的影响,提出一个基于状态的综合维修方案。Tian等 [12] 考虑了一个两阶段退化的生产系统,通过最小化长期平均成本率来优化批量和基于状态的维修阈值。Peng等 [13] 利用更新理论计算退化系统的长期平均成本,提出基于状态的维修方案。以上研究很少将系统退化过程与抽样检验及视情维修方案结合在一起。
在生产系统状态监测的研究中,以往文献大都对生产过程进行定期离线抽样检验或全检,较少考虑抽样次数和在线抽样方案的优化设计。另外,在抽样过程中,由于条件限制和抽样的随机性,很可能会做出误判,从而给生产方和使用方造成经济损失,以往文献对抽样检验误判的影响考虑较少。因此,本文将在线抽样检验的方案设计、抽样检验误判的影响与视情维修相结合,针对退化规律服从伽马过程且存在隐性缺陷的生产系统,在考虑抽样检验成本、误报警检查成本、维修成本、不合格品损失等各类成本的基础上,提出综合经济模型。通过寻找最佳抽检和维修方案,以实现生产系统长期运行单位时间平均损失最小的目的。
2. 问题描述及模型假设
2.1. 问题描述
生产系统在运行过程中受环境、磨损、老化等因素影响,将出现退化现象。退化量是随机变量且与系统运行时长呈正相关关系。当累积退化量超过临界阈值时,系统处于异常状态。异常不影响系统运行,但生产加工的产品的不合格品率会增大。在系统异常无法直观判定时,通过对产品质量的在线抽样检验,以推断系统的运行状态。在抽检过程中,如果样本中的不合格品数大于接收数,则有理由怀疑系统可能存在异常。此时,对系统进行进一步检查,如果确认发生异常,立即停机实施纠正性维修;否则,不进行任何处理,系统将继续运行至下一次抽样。当样本中的不合格品数不大于接收数时,则不进行检查,系统将继续运行至下一次抽样。在经过若干次抽检后,对系统进行预防性维修。为了减小生产运行造成的损失,需要对抽样方案和抽检次数进行优化设计,使系统在单位时间内的平均损失达到最低。
2.2. 模型假设
1) 系统在运行过程中的退化量随时间单调不减,且服从伽马过程。当退化量达到临界阈值时,系统发生异常;
2) 系统仅存在正常和异常两种状态,异常状态不影响系统的运行和生产加工的效率;
3) 在异常状态下运行时,生产加工的产品不合格品率将增大;
4) 系统的运行状态可以通过对产品质量的抽样检验加以判定;
5) 当抽样检验报警时,对系统状态进行检查,检查是完美的,检查的时间可以忽略不计;
6) 考虑两种维修方案:一是当系统运行到指定时间点时,进行预防性维修;二是当发现系统异常时,进行纠正性维修。纠正性维修成本大于预防性维修成本,且两类维修均可使系统恢复到初始状态,即修复如新。维修时间可以忽略不计;
7) 产品的原材料和生产加工成本可以不予考虑。
3. 模型构建
考虑一个以恒定速率r生产单一产品的生产系统,在运行过程中,系统按照单调不减的退化过程退化,每个时间段的退化量累积可加。当退化量达到异常阈值
时,系统即处于异常状态。在时间
内的退化由一个可测量的随机变量
定义。由于伽马过程在描述退化随时间单调累积的广泛适用性,本文假定
服从平稳的伽玛过程。
生产系统的伽马退化过程
具有以下特征:
1)
;
2)
具有独立增量性;
3) 对于所有
,随机变量
服从伽马分布。其密度函数
和分布函数
定义为:
(1)
(2)
其中
,
(
,
)为不完全伽马函数。
当
时,式(1)、(2)可简记为
和
。
由于在累积退化量达到异常阈值
时,系统发生异常。因此,系统正常运行时长可以用随机变量
表示,即退化量首次超过阈值的时刻。其对应的分布函数为:
(3)
系统正s,常运行时长
的密度函数为:
(4)
其中
,
系统在第
次检查时没有发生异常的概率可表示为:
(5)
其中
为第j次抽样检查的时点,h为抽样间隔。
系统在第j个区间发生异常的概率为:
(6)
为了评估系统的运行状态,并减少不合格品带来的损失,对系统实施如下的检查和维修策略:定期对生产过程进行抽样检验,抽样方案为
。在抽样检验时,若样本中的不合格品数Y大于接收数Ac,系统报警。此时,对系统进行检查,以确认系统的状态。若系统异常,则实施纠正性维修。若系统正常,则不对系统实施维修行为,生产继续进行。考虑到系统异常带来的影响及过高的维修成本,计划在系统运行至
时实施预防性维修,使系统恢复到初始状态。
将生产从开始运行到采取维修措施的时长记为一个生产周期。则,在每个生产周期结束时,系统发生一次更新。在抽样检验时,第一类风险
和第二类风险
分别为:
(7)
(8)
其中p0和p1分别是系统在正常和异常状态下生产的产品的不合格品率。
在一个生产周期内,根据系统是否发生异常和抽检是否报警,可将生产过程划分为以下几种情形。
情形1:在运行过程中,系统没有发生异常
系统在运行过程中,由于没有发生异常,生产将运行至
。此时,根据抽检情况,将系统运行分为发生误报警和不发生误报警两种运行轨迹。
1) 没有发生异常,也没有误报警
系统运行正常且没有发生误报警的概率为:
。
记
分别表示第i种情形、第j种运行轨迹的误报警检查成本、纠正性维修成本、不合格品损失、抽检成本。如果在一个生产周期内即没有发生异常,也没有发生误报警,则不存在误报警检查和纠正性维修,即
,
。此时,总损失成本包括不合格品的损失、抽检检验成本和预防性维修成本。
由于系统没有发生异常,故,一个生产周期内生产的不合格品损失为:
(9)
其中,D为单位不合格品损失。
在一个生产周期内,共抽检
次。故,抽检成本为:
(10)
其中,a为抽取一个样本的固定成本,b为抽检单位样品的成本。
此时,平均损失为:
(11)
其中,C5为预防性维修成本。
2) 没有发生异常,但发生误报警
系统运行正常但发生误报警的概率为:
。
如果在一个生产周期内没有发生异常,但发生误报警,则不存在纠正性维修,即
。生产总损失包括误报警检查成本、不合格品损失、抽样检验成本和预防性维修成本。
在发生误报警的条件下,误报警的次数M为随机变量,误报警i次的概率为:
(12)
平均误报警次数为:
。
故,误报警检查成本
,其中
为一次误报警检查成本。
另外,在没有发生异常,但发生误报警的情况下,生产的不合格品损失、抽样检验成本和预防性维修成本与没有发生异常,也发生误报警的情况相同。即
,
。
故,平均损失为:
(13)
因此,当系统在运行过程中,如果没有发生异常,则生产过程的平均损失为:
(14)
情形2:系统发生异常,且实施抽样检验
系统在运行过程,如果异常在第
个区间发生,则在异常发生后最多有
次机会对过程实施抽样检验。异常在第
个区间发生的概率为:
。
根据异常发生前抽样检验是否报警,将系统运行分为两种运行轨迹:没有误报警和发生误报警。在发生异常后,又分为没有漏报警、有漏报警但被发现、有漏报警但没有被发现三种路径。
1) 系统在发生异常前,没有误报警
系统在发生异常前没有误报警的概率为:
。
由于在发生异常前,没有发生误报警,所以误报警检查成本
。
在异常发生的条件下,无论异常能否被发现,都不存在预防性维修,故预防性维修成本
。生产过程的损失包括:纠正性维修成本、生产不合格品损失、抽样检验成本。
① 纠正性维修成本
在异常发生后,如果抽样检验能够发现异常,则对系统进行纠正性维修。纠正性维修成本为:
(15)
如果异常没有发现,在生产周期终点按计划实施预防性维修,但系统实际为异常状态,故最终实施纠正性维修。此时的纠正性维修成本将增大,纠正性维修成本为:
(16)
其中
为纠正性维修成本;
为原计划采用预防性维修,但最终转为纠正性维修的成本。
② 生产不合格品损失
不合格品损失等于异常前和异常后不合格品损失之和。
(17)
式(17)中,第一项表示系统在正常状态下运行生产不合格品的损失;中括号里的第一项表示第j个区间内异常运行时长,第二项表示从第j次抽样检验漏报警到第i次抽样检验报警之间平均异常运行时长,第三项表示从j次抽样检验漏报警持续到生产周期终点的平均异常运行时长。
当
时,在第
次抽检时存在报警和漏报警两种情况。如果报警,则系统停止运行,并进行纠正性维修;如果漏报警,则系统继续运行至生产周期终点。故,生产不合格品损失可表示为:
(18)
③ 抽样检验成本
抽样检验成本包括异常前的抽检成本和异常后的抽检成本。
在系统发生异常前,共抽检了
次。在异常发生后,抽检次数与异常是否被发现有关。
当
时,异常发生后的抽检次数的期望为:
(19)
因此,总的抽检成本为:
(20)
当
时,由于第
次抽检一定发生,故总抽检次数为
。总抽检成本为:
(21)
故,平均损失为:
(22)
2) 系统在发生异常前,存在误报警
系统在发生异常前发生误报警的概率为:
。
在发生误报警的条件下,误报警i次的概率为:
(23)
平均误报警次数为:
。故,误报警检修成本
。
在系统发生异常且存在误报警的情况下,不存在预防性维修,故预防性维修成本
。生产过程中的纠正性维修成本、不合格品损失、抽检成本与不发生误报警情况下的相同。即
,
。
故,平均损失为:
(24)
因此,系统在运行过程中,如果发生异常,且有机会实施抽样检验时,生产过程的平均损失为:
(25)
情形3:系统发生异常,但没有实施抽样检验
系统在第N个区间发生异常的概率为:
。
当系统在第N个区间发生异常时,由于在第N个检测点按计划实施预防性维修,故没有机会对过程进行抽样检验,系统的状态未知。此时,首先按计划进行预防性维修,在维修过程中,发现系统异常后转为纠正性维修。在这种情况下,系统虽然运行至预防性维修点,但并非实施预防性维修,预防性维修成本
此时,生产过程的损失包括:误报警检查成本、纠正性维修成本、不合格品的成本、抽样检验成本。
在异常发生前共抽检了
次,平均误报警次数为:
。
故,误报警检查成本
。
由于在
时,按计划进行预防性维修,但最终实施了纠正性维修。故纠正性维修成本为:
。
不合格品损失等于异常前和异常后不合格品损失之和。故总的不合格品损失为:
(26)
在系统发生异常前,共抽检了
次。在异常发生后,抽检次数为0。因此,总抽检成本为:
。
故,情形3的平均损失为:
(27)
综上,一个生产周期内的平均总损失为:
(28)
一个生产周期的平均总时长为:
(29)
因此,一个生产周期单位时间内的平均损失为:
(30)
本文研究目的是确定抽样方案
、最大抽检次数N,使单位时间平均损失
最小。
4. 仿真模拟与分析
假定生产系统的退化量服从平稳伽马过程
。在退化量达到异常阈值前,系统保持正常运行,在退化量达到异常阈值时,生产系统将发生异常。异常状态不影响生产运行,但产品的不合格品率将增大。为了及时发现系统异常,定期对生产过程进行在线抽样检验,以判定系统的运行状态。根据抽样检验是否报警,采用检查、纠正性维修和预防性维修等多种方案。为了制定最佳的抽样方案检查和维修计划,确定模型参数值如表1所示。

Table 1. Model parameters and their values
表1. 模型参数及其取值
将表1中的参数值代入式(30),通过MATLAB编程计算得:当异常阈值
,抽样间隔
时,最佳抽样方案
,最大抽检次数
,第一类风险
,第二类风险
,一个生产周期内单位时间平均损失
。如果依据
、
及
、
值,可得计数标准型一次抽样检验方案为
,对应的单位时间平均损失
。由计算结果可以看出,标准型一次抽样方案的样本量较大,但对应的单位时间平均损失相较本文所提方案增加0.67。假设生产系统每天按8个单位工作时间计算,一年365天,本文所提方案将减少损失1956.4。
下面通过抽样特征OC曲线和平均检出质量AOQ曲线,进一步对比两种抽样方案的差异。
由图1知,在不合格品率较小和较大时,本文给出的抽样方案与标准型一次抽样方案的接收概率基本一致。在不合格品率介于
和
之间时,本文给出的抽样方案的接收概率略有降低。由图2知,在不合格品率较小时,本文给出的抽样方案与标准型一次抽样方案的AOQ基本一致,但标准型一次抽样方案对应的AOQL相对较差。
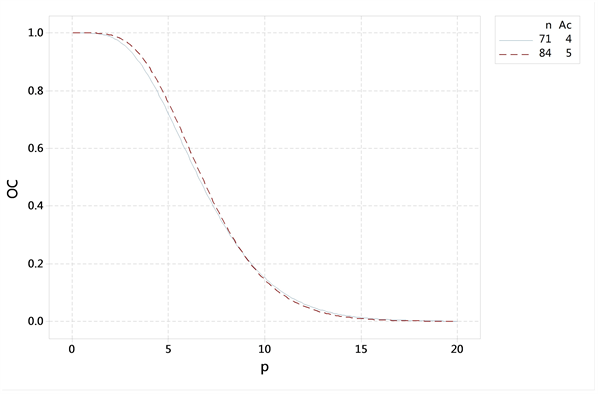
Figure 1. Operating characteristic curve
图1. 抽检特征OC曲线
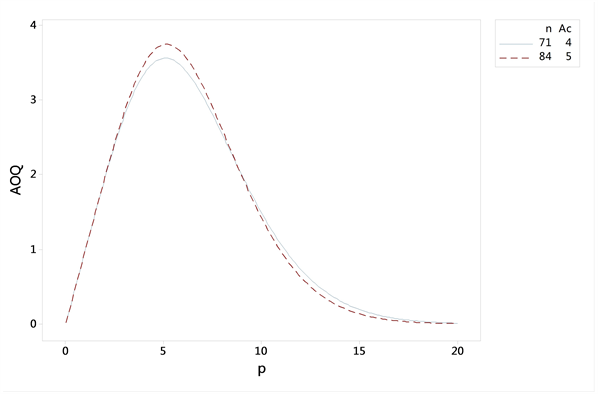
Figure 2. Average Output Quality curve
图2. 平均检出质量AOQ曲线

Table 2. Analysis of the effect of X f on decision variables, two types of risk and average loss per unit of time
表2.
对决策变量、两类风险和单位时间平均损失的影响分析
对于不同的生产系统,其异常阈值有时也有差异。在抽样间隔固定的情况下,研究不同异常阈值对抽样方案、一个生产周期内单位时间平均损失及抽样风险的影响。由表2知,当异常阈值
减小时,在相同的退化规律下,系统发生异常的时间将缩短。此时,抽样方案有放宽趋势,最大抽检次数N逐渐减小,单位时间平均损失
逐渐增大。不同的异常阈值
对第一类风险
的影响较小,对第二类风险
的影响相对较大。当异常阈值
由5减小到1时,抽样方案将由(76, 4)变成(57, 3),单位时间平均损失
由133.53增加到208.89,同比增加了56.44%。

Table 3. Analysis of the effect of p 1 on decision variables, two types of risk and average loss per unit of time
表3.
对决策变量、两类风险和单位时间平均损失的影响分析
当系统处于异常状态时,不合格品率
不同,对应的抽样方案也不相同。由表3知,当
不变,而不合格品率
增大时,
和
之间的距离增大,抽样方案有放宽的趋势,最大抽检次数N保持不变,单位时间平均损失
逐渐减小。同时,第一类风险
和第二类风险
都将逐渐减小。如果
不变,
由0.1增大到0.2,抽样方案将由(71, 4)变成(37, 3),抽样检验工作量降低一半,单位时间平均损失
也由143.83降低到134.12。

Table 4. Analysis of the effect of D on decision variables, two types of risk and average loss per unit of time
表4. 不合格品损失D对决策变量、两类风险和单位时间平均损失的影响分析
不同的产品对应的不合格品损失有时也不尽相同。因此,有必要研究不合格品损失对抽样方案、单位时间平均损失和两类风险的影响。由表4知,当不合格品损失D增大时,抽样方案有加严的趋势,最大抽检次数N变化不大,
先减小后逐渐增大,
逐渐减小。单位时间平均损失
逐渐增大。当单位不合格品损失为40时,在一个生产周期内,单位时间平均损失为296.22。相较于不合格品损失为15,单位时间平均损失将增加152.39,同比增加了105.95%。因此,生产部门可以根据产品不合格造成的损失,选择合适的抽样方案和维修策略,以尽可能地降低损失。
5. 总结
本文研究了服从伽马退化过程的生产系统状态检测和维修方案的优化设计问题。通过对产品的在线抽样检验,推断系统的运行状态。考虑了抽样检验的两类误判风险,提出了单位时间平均损失经济模型。仿真模拟,给出了寻找最佳决策方案的方法,并在两类误判风险条件下,与标准型一次抽样方案进行了对比。最后,分析了模型参数对决策变量和单位时间平均损失的影响。研究表明:异常阈值减小时,抽样方案有放宽趋势,最大抽检次数将减小,单位时间平均损失将增大;异常状态造成不合格品率增大时,抽样方案有放宽趋势,最大抽检次数保持不变,单位时间平均损失将减小;不合格品损失增大时,抽样方案有加严趋势,最大抽检次数变化不大,单位时间平均损失将增大。本文所提模型可以为带有退化的生产系统的状态检测和维修决策提供决策方案。