基于TOPSIS熵权的SARIMA模型对新能源汽车的生态研究

Research on the Ecological Impact of New Energy Vehicles Using the SARIMA Model Based on TOPSIS Entropy Weight

摘要: 自2011年起，新能源汽车在政府的支持和鼓励下快速发展，已呈现出从政策驱动转向市场拉动的新发展阶段，而新能源汽车的发展对生态环境的影响也不容小觑。本文对我国各个省份新能源汽车的发展水平进行聚类划分，从中选择具有代表性的广州省，建立SO₂，NO_x，工业烟(粉)尘作为新能源汽车影响生态环境的指标，利用基于TOPSIS的熵权法对2007年到2021年时间序列的生态环境进行打分，发现广州省的生态环境得分逐年递增。我们将该评价模型推广至全国，并采用SARIMA的时间序列模型对我国新能源汽车的发展进行预测和分析，从政府政策，企业活力，成本支出，基础设施四个方面解释说明影响我国新能源汽车发展的因素，进而验证新能源汽车的发展对我国生态环境的影响，我们发现新能源汽车的发展有利于我国生态环境的改善。

Abstract: Since 2011, with the government’s support and encouragement, new energy vehicles have rapidly developed in China. They have transitioned from policy-driven to market-driven development, and their impact on the ecological environment should not be underestimated. This study clusters and categorizes the development levels of new energy vehicles in different provinces of China. Guangzhou province, which represents the case study, is selected. We use SO₂, NO_x, and industrial smoke (particulate matter) as indicators for the impact of new energy vehicles on the ecological environment. We employ the TOPSIS entropy weight method to score the ecological environment based on a time series from 2007 to 2021 and find an increasing trend in the ecological environment score in Guangzhou province over the years. We extend this evaluation model to the national level and use the SARIMA time series model to forecast and analyze the development of new energy vehicles in China. We explain and validate the factors influencing the development of new energy vehicles in China from four aspects: Government policies, business vitality, cost expenditure, and infrastructure. Subsequently, we verify the impact of the development of new energy vehicles on China’s ecological environment, we find that the development of new energy vehicles is conducive to the improvement of China’s ecological environment.

1. 引言

随着全球不可再生能源的不断枯竭，以及生态环境的恶化，新能源汽车因其能够有效地缓解能源短缺与环境污染问题，近些年来得到了快速发展并受到了各国政府和学者的广泛关注 [1] 。自2011年我国政府大力推动新能源汽车的发展以来，尾气污染不断减少，生活环境不断改善，人民的幸福指数不断提高。然而，随着新能源汽车市场的快速发展，如何准确预测和评估新能源汽车的发展趋势和影响因素成为了当前亟需解决的问题。因此，本研究的目的是将TOPSIS熵权法与SARIMA模型相结合，通过权重分配和时间序列分析，深入探究新能源汽车市场的发展潜力，并为相关决策提供科学依据。大力推动新能源汽车发展有助于减少温室气体的排放，有效缓解全球气候变暖的难题，改善全球的生态环境，助力我国碳中和碳达峰目标的实现 [2] 。

2. 数据预处理

2.1. 数据缺失值处理

由于收集数据的时间跨度较长，数据不全，信息缺失会对建模分析的过程产生影响，人为寻找缺失值并进行处理需要时间，我们利用python建立自动寻找缺失值的系统，并进行三次样条插值法对中间的缺失值进行处理，利用matlab工具箱对时间序列首尾缺失的值进行拟合回归。

2.2. 数据标准化

为了消除不同量纲对于数据分析的影响，我们建立数据量的矩阵，并将矩阵标准化，标准化公式如下：

$Z_{ij}=\frac{X_{ij}}{\sqrt{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{X}_{ij}^2}}}$ (1)

3. TOPSIS的熵权法生态环境评分建立

为了探究各个省份的新能源汽车发展对生态环境的影响，需要定量化各个省份的新能源汽车的发展水平，我们将新能源汽车在该省份的普及率作为该省份新能源汽车发展水平的衡量因素，并将新能源汽车对生态环境的影响量化得分，分析该省份新能源汽车的发展对生态环境的影响。

我们定义：

新能源汽车的普及率 = 新能源汽车的销售量/汽车行业的销售量

Step 1：

根据新能源汽车的发展水平对各个省份聚类，选择出代表性的省份，为了探究新能源汽车在整个汽车行业的占比，我们将引入中国各个省份的新能源电动汽车的普及率，并对各省份新能源电动汽车的发展水平进行聚类，聚类结果如图1。

Figure 1. Clustering results

图1. 聚类结果

从图1可以看出，各个省份新能源汽车的普及率可以大致分为3类，我们将其定义新能源汽车发展的高中低三个水平。

Step 2：

为了提高结果的准确性，选择新能源汽车发展水平较高的省份，广东省作为代表，以2014年为时间转折点，分析生态环境在新能源汽车普及前后的变化情况。

并将影响生态环境的指标定义为汽车在制造和行车过程中SO₂，NO_X，工业烟(粉)尘这三个指标的排放量，为了定量分析影响生态环境的程度，我们利用基于TOPSIS的熵权法对生态环境的三个指标确定权重 [3] ，并根据最后结果对生态环境的变化情况进行打分。

1) 在我们建立的数学模型中有n个要评价的对象，m个要评价的指标，n = 15，m = 3。SO₂，NO_X，工业烟(粉)尘均为成本性指标，将指标正向化：

$x_{nm}=\max \left\{\left|x_n-x_{best}\right|\right\}$ (2)

2) 并将正向化指标标准化：

$Z=\left[\begin{array}{cccc}{z}_{11}& z_{12}& \cdots & z_{1m}\\ z_{21}& z_{22}& \cdots & z_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ z_{n1}& z_{n2}& \cdots & z_{nm}\end{array}\right]$ (3)

3) 构造概率矩阵P：

$p_{ij}=\frac{z_{ij}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{z}_{ij}}}$ (4)

4) 对于第j个指标的信息熵

$e_j=-\frac{1}{\ln n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{p}_{ij}}\ln \left(p_{ij}\right)\left(j=1,2,\cdots ,m\right)$ (5)

5) 求得信息效用值

$d_j=1-e_j$ (6)

6) 将信息效用值归一化得到每个指标的熵权见表1：

Table 1. The entropy weight of the three indicators

表1. 三个指标的熵权

$W_j=\frac{d_j}{{\displaystyle \underset{i=1}{\overset{m}{\sum }}{d}_j}}\left(j=1,2,\cdots ,m\right)$ (7)

7) 定义第 $i\left(i=1,2,\cdots ,n\right)$ 个评价对象与最大值的距离和最小的距离：

$D_i^{+}=\sqrt{w_j{\displaystyle \underset{j=1}{\overset{m}{\sum }}{\left(Z_j^{+}-z_{ij}\right)}^2}},D_i^{-}=\sqrt{w_j{\displaystyle \underset{j=1}{\overset{m}{\sum }}{\left(Z_j^{-}-z_{ij}\right)}^2}}$ (8)

8) 计算生态环境得分见表2：

Table 2. Ecological environment score of Guangzhou province

表2. 广州省生态环境得分

$S_i=\frac{D_i^{-}}{D_i^{+}+D_i^{-}}$ (9)

我们将这15年分为两个阶段，分别代表新能源汽车发展前期，新能源汽车发展后期，从图2我们可以看出新能源汽车发展后，广州省生态环境得分不断提高，说明新能源汽车的普及对生态环境有明显改善。

Figure 2. Ecological environment score and pollutant changes in Guangzhou province from 2007 to 2023

图2. 2007年~2023年广州省生态环境得分和污染物变化

4. SARIMA模型的建立

我们将新能源汽车的发展推广至全国，分析近六年来我国新能源汽车的发展现状，并预测未来10年的发展情况，探究我国新能源汽车发展对我国生态环境的影响。

4.1. 近六年新能源汽车发展现状

我们定义近六年新能源汽车发展表现在新能源汽车的市场销量上。

从图3可以看出，近六年我国每月的新能源汽车的销量有指数上升的趋势，且每年我国新能源汽车的销量呈现年前高年中低具有季节性的趋势。

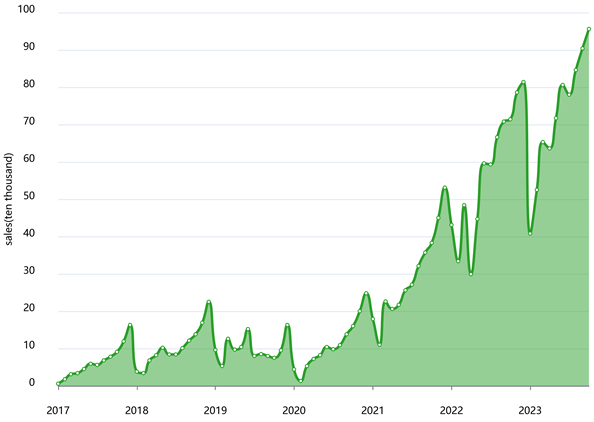
Figure 3. Time series analysis of China’s monthly sales of new energy vehicles in the past six years

图3. 近六年我国新能源汽车月度销量时间序列分析

我们认为春节前新能源电动汽车销量快速增长的原因在于消费者和供给商与经销商三个主体，前者表现在年末人均经济水平的提高，经济拉动消费增长增强了新能源汽车的购买数量；后者表现在厂家依据年前的销量走势，为了刺激销量持续增长而采取的优惠促销，经销商为了减少贴息贷款的费用，促销卖出新能源电动汽车，进而刺激了年前新能源电动汽车销量的增长，而春节期间，消费者的消费欲望并不是很强 [4] 。

从而呈现出一年中12月即春节前新能源电动汽车的销量最高，春节后大概在1月或2月新能源电动汽车的年销量最低，但整体呈现指数上涨的趋势。

4.2. SARIMA模型的建立

根据上述描述，我们发现近六年来我国的新能源电动汽车销量呈现季节性趋势，SARIMA模型见图4是基于时间序列预测对平稳非白噪声的季节性序列进行预测分析，符合季节性平稳变化的规律 [5] 。

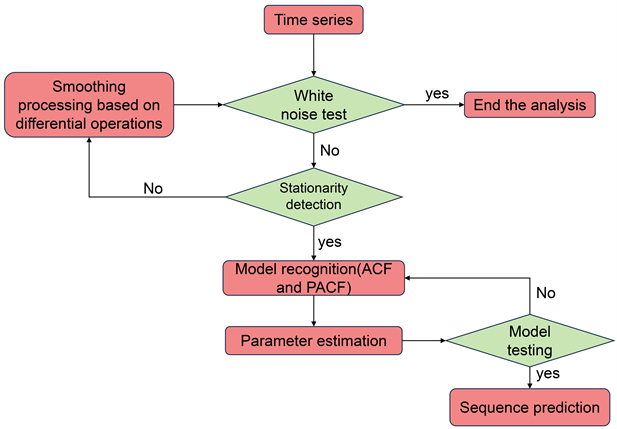
Figure 4. Flowchart of the SARIMA model establishment

图4. SARIMA模型建立的流程图

1) 差分处理

我们对过去六年的新能源汽车的销量进行一阶差分处理并剔除异常值，将其转换为平稳的时间序列后再进行预测，并将销量导入到spss中，可以发现当我们采用ARIMA(p, d, q)(P, D, Q) m时模拟效果最好。

其中AR为自回归项，p = 0为非季节部分对应的自回归项，d = 1为非季节性部分的差分阶数，MA为移动平均项，q = 0为非季节性部分移动平均项的项数；P = 0为季节部分对应的自回归项，D = 1为季节部分的差分阶数，Q = 0为季节部分的移动平均项的项数，m = 12为年度周期数12.

差分自回归移动平均模型的数学表达式如下：

$\left(1-{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\alpha }_i{L}^i}\right)\left(1-{\displaystyle \underset{i=1}{\overset{P}{\sum }}{\alpha }_i{L}^{mi}}\right){\left(1-L\right)}^d{\left(1-L^m\right)}^D{x}_t={\alpha }_0+\left(1+{\displaystyle \underset{i=1}{\overset{q}{\sum }}{\beta }_i}{L}^i\right)\left(1+{\displaystyle \underset{i=1}{\overset{Q}{\sum }}{\beta }_i}{L}^{mi}\right){\epsilon }_t$ (10)

2) 残差检验

经过一阶差分后，一阶差分的序列的稳定性有了显著性提高，我们对模型的白噪声进行残差性检验，进一步提高模型的准确度。

模型的自相关系数(ACF)和偏自相关系数(PACF)图如下。

从图5白噪声的残差检验中可以看出，所有滞后的自相关系数均和0没有显著差异，即没有相关性，我们可以认为数据能够通过白噪声检验。

Figure 5. Residual test for white noise

图5. 白噪声的残差检验

从表3杨博克斯Q检验得到P值 = 0.473 > 0.05，不能拒绝原假设，可认为残差就是白噪声序列，因此我们认为ARIMA(0, 1, 0)(0, 1, 1)可以很好的识别模型。

Table 3. Parameter specification

表3. 参数表格

3) 模型预测

我们对过去6年的新能源电动汽车的销量进行拟合和预测，R² = 0.991，模型与过去六年的新能源销量得到一个很好的拟合，变化趋势和真实的趋势一致如图6所示，因此我们预测未来十年新能源汽车的销量呈现季节性上升趋势，在每年春节前销量达到全年峰值。

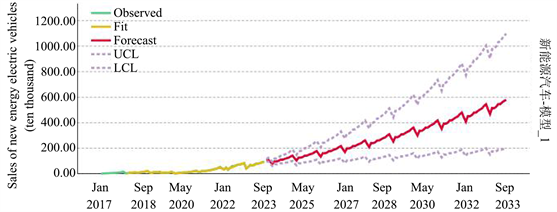
Figure 6. Fitting and forecasting the sales volume of new energy electric vehicles

图6. 对新能源电动汽车销量的拟合和预测

预测部分结果见表4：

Table 4. Sales of new energy vehicles in the next 10 years

表4. 新能源汽车未来十年销量

4.3. 全国新能源汽车推广前后生态环境评分

我们通过SARIMA模型得出近六年我国新能源汽车的销量呈现季节性指数上升趋势，并预测了未来十年的新能源汽车的发展，我们有理由说明在近二十年内，我国新能源汽车的发展呈现整体向好的趋势。

我们将应用在广州省新能源汽车普及前后对生态环境的评价模型推广至全国，如图7所示，我们可以看出自2011年新能源汽车普及之后，生态环境的得分得到明显的提高，说明新能源汽车的普及有利于改善生态环境，有助于碳中和碳达峰的目标实现。

5. 影响新能源汽车发展的因素

根据SARIMA模型和TOPSIS的熵权法的推论，我们可以得到新能源汽车的发展有助于生态环境的改善，由于探讨影响新能源汽车的发展的因子对生态环境的改善具有重要意义，我们将从政府政策，企业活力，成本价格，基础设施四个方面来评估对新能源汽车发展的影响 [6] 。

Figure 7. The ecological environment score of new energy vehicles in China

图7. 全国新能源汽车的生态环境得分

1) 通过收集数据，我们得到影响新能源电动汽车发展的相关因子，将新能源电动汽车的发展量化为电动汽车的销量，并构造了三级指标结构表如图8：

Figure 8. Three-level index structure table affecting new energy vehicles

图8. 影响新能源汽车的三级指标结构表

2) 我们得到三级指标的斯皮尔曼相关系数，并将这些指标与新能源电动汽车的销量的相关程度可视化，如图9所示。从图中可以看出油价和动力电池的公司注册数对新能源电动汽车的销量影响并不是很大，因此我们将这两个指标剔除掉，将剩下7个指标作为影响新能源电动汽车销量的输入变量。

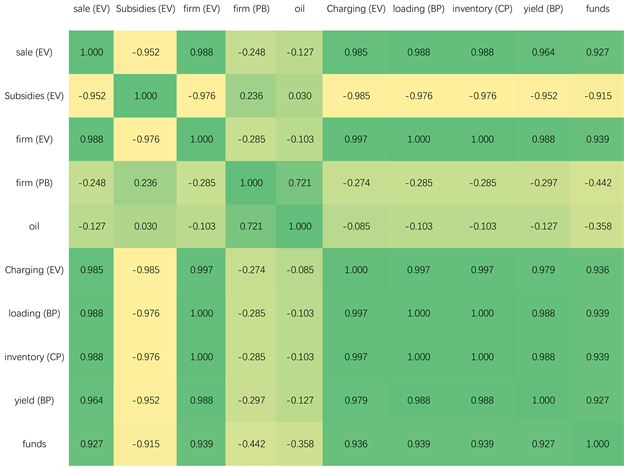
Figure 9. Spearman correlation coefficient heat map

图9. 斯皮尔曼相关系数热图

3) 我们将7个指标作为输入变量，新能源电动汽车销量作为输出变量，构造多元回归模型，通过t检验我们发现绝大多数指标并不显著，为精准确定7个指标标量与新能源电动汽车销量的关系，我们对指标进行BP检验看扰动项是否存在异方差，并进行多重共线性 [7] 的检验，检验参数如表5所示。

Table 5. Verification parameter table

表5. 检验参数表

可以看出BP检验的P值均小于0.05，说明扰动项并不存在异方差，但是我们发现VIF均大于10，说明这7个指标变量存在多重共线性。

4) 对解决7个指标变量多重共线性的干扰，我们采用向后逐步回归进行分析，剔除掉具有完全多重共线性的指标变量，得到的回归系数如表4所示。

构造逐步向后回归模型表达式：

$销量=0.7903058\times 电池装车量+0.8083368\times 充电桩保有量$ (11)

可以定量分析动力电池的装车量和充电桩的保有量与新能源电动汽车的销量的变化趋势具有趋同性，虽然补贴呈现“下坡”趋势，但考虑到实时政策的有效性，我们将政府政策这个二级指标单独做出解释，在新能源电动汽车的发展之初，我国为了促进新能源电动汽车的发展，对新能源电动汽车投入大量资金并对新能源电动汽车进行补贴，提高了新能源电动汽车企业的自主创新能力，因而新能源电动汽车的续航里程等关键技术得到有效提升，为了提高市场上新能源电动汽车的质量，我国根据续航里程对新能源电动汽车的补贴做出调整，续航里程高则补贴较同期其他新能源电动汽车的补贴高，刺激企业的核心竞争力，续航里程的提高也表现了新能源电动汽车的发展向好趋势。

6. 结论与展望

我国新能源汽车市场规模不断扩大，企业核心竞争力不断提高，产销呈现爆炸式增长，同时有助于生态环境的改善，本文通过TOPSIS的熵权法建立新能源汽车对生态环境影响的评价模型，具有一定的客观性，将其运用至广州省并推广至全国，二者的结果都说明了新能源汽车的发展有助于生态环境的改善。

考虑到影响新能源汽车发展的因素会间接影响对生态环境的改善，本文通过政府政策，企业活力，成本价格，基础设施四个方面建立起和新能源电动汽车发展的关系，并运用斯皮尔曼相关系数，多元回归验证因素对新能源汽车发展的影响。

本文提出的模型能够定量化评价新能源汽车对生态环境的影响，并且预测未来新能源汽车的发展，并进一步探讨了影响新能源汽车发展的因素，使用TOPSIS熵权法对新能源汽车影响环境的相关指标进行权重分配，从而确定各个指标的重要性。通过这种方式，可以更全面地考虑各个指标的影响，通过SARIMA模型预测新能源汽车的发展，讨论新能源汽车的发展和环境的改善是否具有趋同性，提高预测结果的准确性。此外，该研究还可以为新能源汽车相关决策提供科学依据，帮助制定有效的发展策略，客观而全面地认识了新能源汽车发展对生态环境的影响，具有重要现实意义。