多无人机同时到达的可解集算法

On Solving Simultaneous Arrival Problems for Multiple UAVs System

摘要: 随着无人机技术的快速发展，研究多无人机协同运动具有重要的现实意义。本文针对多架同质的无人机，在障碍约束下考察其同时到达给定目标区域的问题。我们基于距离聚类的Euler方法构造近似可解集，进而获得障碍情境下多无人机的可行轨迹。最后，数值仿真证明了理论结果的有效性。

Abstract: With the rapid advancement of unmanned aerial vehicle (UAV) technology, there exists a significant practical need to explore the collaborative motion of multiple UAVs. This paper investigates the simultaneous arrival problem of multiple unmanned aerial vehicles avoiding obstacles. The technique presented in the paper is based on constructions of the approximate solvability sets. The approximate solvability sets are constructed using the Euler method and selected by distance clustering. Subsequently, we analyze the obstacle situation for this system. Finally, we present simulation results to demonstrate the effectiveness of our theoretical results.

1. 引言

随着科技的迅猛发展，无人机编队控制技术逐渐成为人工智能和航空领域的热门研究方向 [1] 。无人机，具备高机动性、强隐蔽性、低成本和灵活操作等特点，已经在军事和民用领域广泛应用，为各行各业带来了全新的可能性。例如，在灾害评估和监视任务中，多架无人机可以协同搜索更大的区域，提高效率 [2] 。而在军事任务中，多架无人机的协同攻击能力可以通过多方位覆盖实现更为精准和高效的目标打击 [3] 。在实际作战任务中，多架无人机的协同配合能够通过能力互补提升整个无人机系统的作战效能 [4] 。为了提高攻击的有效性和打击的突然性，可以设计多架无人机从不同的初始位置起飞，先集结到一个位置形成紧密编队，然后从多个方向同时对一个或多个地面目标进行攻击。而本文的研究重点在于确保不同初始位置的多架无人机在控制作用下能够同时到达指定的目标区域。

早期对于多架无人机同时到达问题的研究多以路径规划为主 [5] 。McLain等提出了基于协调变量与协调函数的协同控制方法，通过路径规划实现了多架无人机同时到达的目标 [6] 。为了实现通信拓扑动态变化的目标，同时解决 [5] 和 [6] 中集中式控制方法的缺陷，Beard等提出了一种基于一致性算法的分散化解决方案 [7] 。此外，Neto等基于快速搜索随机树(RRT)算法，提出了多架无人机在障碍约束下的可行轨迹 [8] 。针对现实中无人机之间通信延迟等情况，Makhdoom等通过周期性调整无人机的速度和任务轨迹，保证了在通信受限的情况下，多架无人机同时到达目标位置 [9] 。以上的研究主要基于一致性算法进行正向求解，较少关注问题的逆向求解。目标逼近算法因其能够在相对短的时间内迅速收敛到较优解，提高了问题求解的效率。此外，该算法通常具备一定的自适应性，能够适应环境的变化，在不同条件下依然能够有效运行。为了确保多架无人机能够同时到达指定的目标区域，我们将多架无人机同时到达的问题转化为目标逼近问题(approach problem)，并采用逆向求解的方法。

值得指出的是，目标逼近问题的其中一种求解方法是使用可解集(solvability sets)来构造问题的解 [10] [11] [12] [13] [14] 。能够使无人机系统到达指定目标区域的初始状态集合称为系统的可解集。Ushakov等使用构造系统的可达集(attainability sets)与积分漏斗(integral funnels)的技术通过逆向求解逐步计算出了非线性控制系统的近似可解集，应用Euler方法在每个时间区间内由分段常值控制得到了对应的欧拉多边形线 [15] ，并提出像素法(pixel method) [16] 来提高计算可解集的效率。Ershov等基于Ushakov的算法研究了在相位约束下控制系统的逼近问题，并依据可解集的概念给出了逼近问题的近似解 [17] 。

本文主要研究Menon等提出的三维空间中的非线性多无人机模型 [18] ，在Ushakov算法基础上，为提高计算效率，通过基于距离聚类的Euler方法来构造近似可解集。进一步探讨多架无人机同时到达的航迹规划问题，在确保无人机之间和无人机与障碍物不发生碰撞的前提下，实现多架无人机同时到达指定的目标区域。

本文主要分为以下五个部分：第二部分介绍了基本模型与问题描述，第三部分讨论了模型求解方法，并且研究了如何避免无人机之间以及无人机与障碍物之间的碰撞问题，第四部分进行了数值模拟实验，最后对研究内容进行了总结，并提出了未来可研究的方向。

2. 预备知识

2.1. 无人机模型

假设编队中每架无人机采用 [18] 中的模型来描述无人机的飞行运动，不考虑地球曲率的影响，在时间段 $\left[t_0,\theta \right]$ 上，其中，无人机编队中每架无人机的运动模型可以描述为

$\begin{array}{l}\stackrel{\dot{}}{x}=v\cos \alpha \cos \beta \\ \stackrel{\dot{}}{y}=v\cos \alpha \sin \beta \\ \stackrel{\dot{}}{z}=v\sin \alpha \end{array}$ (1)

其中 ${\left[x,y,z\right]}^{\text{T}}$ 为无人机在惯性坐标系中的位置坐标，v为无人机相对于地面坐标系的运动速度，下文简称地速； $\alpha$ 为航迹角， $\beta$ 为偏航角。动力学模型可以描述为

$\begin{array}{l}\stackrel{\dot{}}{v}=\frac{T-D}{m}-g\sin \alpha \\ \stackrel{\dot{}}{\alpha }=\frac{g}{v}\left(n_g\cos \varphi -\cos \alpha \right)\\ \stackrel{\dot{}}{\beta }=\frac{L^0\sin \varphi }{mv\cos \alpha }\end{array}$ (2)

其中m为无人机的质量，g为重力加速度， $L^0$ 为升力，D为阻力，T为无人机发动机产生的推力控制量， $\varphi$ 为无人机方向舵与副翼产生的滚转角控制量， $n_g=L^0/\left(mg\right)$ 为无人机升降舵产生的过载控制量。

在 [19] 中，对运动模型(1)进一步求导得到：

$\ddot{x}=u_x$ ， $\ddot{y}=u_y$ ， $\ddot{z}=u_z$

其中 $u_x$ ， $u_y$ ， $u_z$ 与实际控制量之间的关系为

$\begin{array}{l}T=m\left[\left(u_z+g\right)\sin \alpha +u_{xy}\cos \alpha \right]+D\\ n_g=\frac{\left(u_z+g\right)\cos \alpha -u_{xy}\sin \alpha }{g\cos \varphi }\\ \varphi =\arctan \left[\frac{u_y\cos \beta -u_x\sin \beta }{\left(u_z+g\right)\cos \alpha -u_{xy}\sin \alpha }\right]\end{array}$ (3)

其中 $u_{xy}=u_x\cos \beta +u_y\sin \beta$ ，航迹角 $\alpha =\arcsin \left(\stackrel{\dot{}}{z}/v\right)$ ，偏航角 $\beta =\arctan \left(\stackrel{\dot{}}{y}/\stackrel{\dot{}}{x}\right)$ 。

设 $\xi ={\left[x,y,z,v,\alpha ,\beta \right]}^{\text{T}}$ ， $u={\left[u_x,u_y,u_z\right]}^{\text{T}}$ ，将(3)代入无人机运动与动力学模型(1)(2)，可以将无人机模型描述为如下形式

$\frac{\text{d}\xi }{\text{d}t}=f\left(t,\xi ,u\right)$ ， $t\in \left[t_0,\theta \right]$ ， $u\in P$ (4)

其中t表示时间。考虑到 $\alpha$ 与v的实际意义， $\alpha \in \left[-{\alpha }_0,{\alpha }_0\right]\subset \left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ ， $v\in \left[a,b\right]$ ，其中 $a,b>0$ ， $\xi \in {ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]\subset {ℝ}^6$ 为系统状态变量， $u={\left[u_x,u_y,u_z\right]}^{\text{T}}\in P$ 为控制输入向量，P为欧氏空间 ${ℝ}^3$ 中的紧集。

对系统(4)分析，满足如下条件：

条件1向量函数 $f\left(t,\xi ,u\right)$ 在 $\left[t_0,\theta \right]\times {ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]\times P$ 上有界且连续可微，且对于任意有界闭区域 $D\subset \left[t_0,\theta \right]\times {ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]$ ，存在常值 $L=L\left(D\right)\in \left(0,\infty \right)$ 使得

$\Vert f\left(t,{\xi }^{\left(1\right)},u\right)-f\left(t,{\xi }^{\left(2\right)},u\right)\Vert \le L\Vert {\xi }^{\left(1\right)}-{\xi }^{\left(2\right)}\Vert$ ， $\left(t,{\xi }^{\left(i\right)},u\right)\in D\times P$ ， $i=1,2$ ，

其中 $\Vert f\Vert$ 为f在欧式空间的范数，且连续函数 $f\left(t,\xi ,u\right)$ 的解可以在D内延展。

条件2对于任意的 $\left(t,\xi \right)\in \left[t_0,\theta \right]\times {ℝ}^4\times \left[{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]$ ， $F\left(t,\xi \right)=\left\{f\left(t,\xi ,u\right):u\in P\right\}\subset D$ 是凸集。考虑到条件1中D的定义，假设 $\omega \left(\delta \right)=max\left\{\Vert f\left(t^{\left(1\right)},\xi ,u\right)-f\left(t^{\left(2\right)},\xi ,u\right):\left(t^{\left(i\right)},\xi ,u\right)\in D\times P,\left|t^{\left(2\right)}-t^{\left(1\right)}\right|\le \delta ,\delta \in \left(0,\infty \right),i=1,2\Vert \right\}$ 其中当 $\delta \to 0$ 时 $\omega \left(\delta \right)\to 0$ 。定义紧集A，B之间的Hausdorff距离为 $d\left(A,B\right)$ ，则

$d\left(F\left(t^{\left(1\right)},{\xi }^{\left(1\right)}\right)-F\left(t^{\left(2\right)},{\xi }^{\left(2\right)}\right)\right)\le \omega \left(\delta \right)+L\Vert {\xi }^{\left(1\right)}-{\xi }^{\left(2\right)}\Vert ,\left(t^{\left(1\right)},{\xi }^{\left(1\right)}\right),\left(t^{\left(2\right)},{\xi }^{\left(2\right)}\right)\in D,\left|t^{\left(1\right)}-t^{\left(2\right)}\right|\le \delta$ .

2.2. 问题描述

假设无人机系统(4)中的N个成员从不同位置出发并同时到达指定目标区域 $T_{*}$ ， $M\subset {ℝ}^6$ 为空间中的一个紧集,且 $T_{*}=\left\{{\left(x,y,z\right)}^{\text{T}}:{\left[x,y,z,v,\alpha ,\beta \right]}^{\text{T}}\in M\right\}$ 。为实现多无人机安全到达目标区域，需要解决如下问题：

问题1 求解系统(4)的可解集 $\mathcal{W}=\left\{\left(t_{*},{\xi }_{*}\right):t_0\le t_{*}<\theta ,\xi \left(t_{*}\right)={\xi }_{*}\right\}$ ，满足对任意的 $\left(t,\xi \right)\in \mathcal{W}$ ，总是存在容许控制 $u\left(t\right)\left(t\in \left[t_0,\theta \right]\right)$ ，保证 $t=\theta$ 时无人机能够到达目标区域，即 $\xi \left(\theta \right)\in M$ 。

问题2 对 $\left(t^{\left(0\right)},{\xi }^{\left(0\right)}\right)\in \mathcal{W}$ ，构造容许控制 $u^{*}\left(t\right)$ ，形成运动轨迹 ${\xi }^{*}\left(t\right)$ $\left(t\in \left[t_0,\theta \right]\right)$，使 $t=\theta$ 时无人机能够到达目标区域，即 ${\xi }^{*}\left(\theta \right)\in M$ 。

问题3 假设 $\left(t,\xi \right)\in \mathcal{W}$ ，寻找可以避免无人机之间及无人机与障碍物碰撞的容许控制 $\bar{u}\left(t\right)$ ，形成运动轨迹 $\bar{\xi }\left(t\right)$ $\left(t\in \left[t_0,\theta \right]\right)$，使 $t=\theta$ 时无人机能够到达目标区域，即 $\bar{\xi }\left(\theta \right)\in M$ 。

3. 多架无人机系统的目标到达问题

第三部分采用构造近似可解集的方法解决多架无人机系统的目标到达问题。由于编队中每架无人机的运动模型相同，本节重点分析单架无人机系统。首先对无人机系统进行逆向分析，同时使用Euler方法对控制输入为分段常值的系统进行求解。

3.1. 多无人机目标到达问题的近似可解集

为解决问题1，我们通过构造可解集来描述系统(4)的近似解。

在许多控制问题与博弈问题中，可解集可以使用可达集与积分漏斗来构造 [15] 。对于系统(4)，可解集 $\mathcal{W}$ 是 $\theta$ 时刻目标逼近问题可解的初始状态集合，即问题1的解，满足在任意 $\mathcal{W}$ 中的初始状态 $\left\{\left(t_{*},{\xi }_{*}\right):t_0\le t_{*}<\theta ,\xi \left(t_{*}\right)={\xi }_{*}\right\}$ ，从而在控制作用下 $\theta$ 时刻有 $\xi \left(\theta \right)\in M$ 。系统(4)在 ${ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]$ 空间的可达集可以表示为

$X\left(t^{*},t_{*},{\xi }_{*}\right)\left({\xi }_{*}\in {ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right],t_0\le t_{*}<t^{*}\le \theta \right)$

其中 $\xi \left(t_{*}\right)={\xi }_{*}$ 为在 $t=t_{*}$ 时的状态向量， $X\left(t^{*},t_{*},{\xi }_{*}\right)$ 为在 $t^{*}$ 时刻状态向量的集合。由此，积分漏斗可表示为

$X\left(t_{*},{\xi }_{*}\right)={\displaystyle \underset{t^{*}\in \left[t_{*},\theta \right]}{\cup }\left(t^{*},X\left(t^{*},t_{*},{\xi }_{*}\right)\right)}$ $\left(\left(t_{*},{\xi }_{*}\right)\in \left[t_0,\theta \right]\times {ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]\right)$ 。

假设可达集 $Y\left(t^{*},t_{*},{\xi }_{*}\right)$ 满足微分包含关系

$\frac{\text{d}\xi }{\text{d}t}\in F\left(t,\xi \right)$ ， $\xi \left(t_{*}\right)={\xi }_{*}$ ，

则可达集 $X\left(t^{*},t_{*},{\xi }_{*}\right)$ 与 $Y\left(t^{*},t_{*},{\xi }_{*}\right)$ 是一致的，集合 $X\left(t^{*},t_{*},{\xi }_{*}\right)$ 是闭集。由 $X\left(t^{*},t_{*},{\xi }_{*}\right)$ 有界，对于任意的 $\left(t_{*},x_{*}\right)\in \left[t_0,\theta \right]\times {ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]$ ， $t^{*}\in \left[t_{*},\theta \right]$ ，集合 $X\left(t^{*},t_{*},{\xi }_{*}\right)$ 在 ${ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]$ 中是紧集。

为解决无人机系统(4)的目标逼近问题，可以考虑对系统进行逆向时间(backward time)分析 [15] 。对应正向的时间 $t\in \left[t_0,\theta \right]$ ，定义逆向时间 $\tau =t_0+\theta -t\in \left[t_0,\theta \right]$ ，则系统(4)转换为

$\frac{\text{d}\zeta }{\text{d}t}=g\left(\tau ,\zeta ,v\right)$ ， $\tau =t_0+\theta -t\in \left[t_0,\theta \right]$ ， $v\in P$ ， (5)

其中 $g\left(\tau ,\zeta ,v\right)=-f\left(t_0+\theta -\tau ,\zeta ,v\right)$ ， $\left(\tau ,\zeta ,v\right)\in \left[t_0,\theta \right]\times {ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]\times P$ 。

假设初始状态集合 $\left\{\left(t_0,{\zeta }_0\right):{\zeta }_0\in M\right\}$ ，定义 $\mathcal{Z}={\displaystyle \underset{{\zeta }_0\in M}{\cup }Z}\left(t_0,{\zeta }_0\right)$ 为系统(5)的积分漏斗，因此对于 $\mathcal{W}\left(t\right)=\left\{w\in {ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]:\left(t,w\right)\in \mathcal{W}\right\}$ ， $t\in \left[t_0,\theta \right]$ ，满足

$\mathcal{W}\left(t\right)=\mathcal{Z}\left(\tau \right)=\left\{\zeta \in {ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]:\left(\tau ,\zeta \right)\in \mathcal{Z}\right\}$ ， $t=t_0+\theta -\tau$ ， $\tau \in \left[t_0,\theta \right]$ 。

由于 $\mathcal{Z}$ 为 $\left[t_0,\theta \right]\times {ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]$ 中的紧集，因此由上述对应关系， $\mathcal{W}$ 为 $\left[t_0,\theta \right]\times {ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]$ 中的紧集。

在 $\tau$ 时间轴上，对时间段 $\left[t_0,\theta \right]$ 进行有限分割 $\Gamma =\left\{{\tau }_0=t_0,{\tau }_1=t_1,\cdots ,{\tau }_N=\theta \right\}$ ，其中步长 ${\Delta }_i={\tau }_{i+1}-{\tau }_i=\Delta >0$ $\left(i=\overline{0,N-1}\right)$ 都是相同的且 $\Delta \left(\Gamma \right)=\Delta$ 的数值很小。

对于每个 $\mathcal{Z}\left({\tau }_i\right)$ $\left(i\in \overline{1,N-1}\right)$ 和 $\mathcal{Z}={\displaystyle \underset{{\zeta }_0\in M}{\cup }Z}\left(t_0,{\zeta }_0\right)$ 满足如下递推关系

$\mathcal{Z}\left({\tau }_{i+1}\right)=Z\left({\tau }_{i+1},{\tau }_i,\mathcal{Z}\left({\tau }_i\right)\right)$ ， $i=\overline{0,N-1}$ ， (6)

其中 $Z\left({\tau }^{*},{\tau }_{*},Z_{*}\right)$ 为系统(5)在时间 ${\tau }^{*}\in \left[t_0,\theta \right]$ ，由集合 $\left\{\left({\tau }_{*},{\zeta }_{*}\right),{\zeta }_{*}\in Z_{*}\right\}$ $\left({\tau }_{*}\in \left[t_0,{\tau }^{*}\right]\right)$ 中的初始状态得到的可达集。

事实上，对于非常小的时间间隔 $\Delta$ ，在每个瞬时时刻 ${\tau }_i$ ，即使M有着简单的几何形状我们都无法精确计算集合 $Z\left({\tau }_{i+1},{\tau }_i,\mathcal{Z}\left({\tau }_i\right)\right)$ 。因此，我们需要对这些集合进行近似计算。

令 ${\mathcal{Z}}^a\left({\tau }_{i+1}\right)$ $\left(i=\overline{0,N-1}\right)$ 为 ${ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]$ 中 $\mathcal{Z}\left({\tau }_{i+1}\right)$ 的近似，且 ${\mathcal{Z}}^a\left({\tau }_{i+1}\right)$ 为有限集。假设存在充分大的有界闭区域 $D_m=\left\{\left(\tau ,\zeta \right):\left(\tau ,\zeta \right)\in \left[t_0,\theta \right]\times D\right\}=\left\{\left(t,\xi \right):\left(t,\xi \right)\in \left[t_0,\theta \right]\times D\right\}$ ，集合 $\mathcal{W}$ 与集合 $\mathcal{Z}$ 都包含在其中，其中 $D\subset {ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]$ ，在构造过程中我们使用到了上述区域。

定义映射 $\left({\tau }^{*},{\tau }_{*},Z_{*}\right)\mapsto Z^{\left(\delta \right)}\left({\tau }^{*},{\tau }_{*},Z_{*}\right)$ ，其中 $t_0\le {\tau }_{*}<{\tau }^{*}\le \theta$ 且 $\delta ={\tau }^{*}-{\tau }_{*}$ ， $Z_{*}$ 是 ${ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]$ 中的有限集，在上述条件下有

$Z^{\left(\delta \right)}\left({\tau }^{*},{\tau }_{*},Z_{*}\right)={\displaystyle \underset{{\zeta }_{*}\in Z_{*}}{\cup }{Z}^{\left(\delta \right)}}\left({\tau }^{*},{\tau }_{*},{\zeta }_{*}\right)$ ， (7)

$Z^{\left(\delta \right)}\left({\tau }^{*},{\tau }_{*},Z_{*}\right)={\zeta }_{*}-\delta F^{\left(\delta \right)}\left({\tau }_{*},{\zeta }_{*}\right)$ ， (8)

其中映射 $\left({\tau }_{*},{\zeta }_{*}\right)\mapsto F^{\left(\delta \right)}\left({\tau }_{*},{\zeta }_{*}\right)$ $\left(\left({\tau }_{*},{\zeta }_{*}\right)\in D_m\right)$ 是 $\left({\tau }_{*},{\zeta }_{*}\right)\mapsto F\left({\tau }_{*},{\zeta }_{*}\right)$ $\left(\left({\tau }_{*},{\zeta }_{*}\right)\in D_m\right)$ 的有限数值近似，且 $F^{\left(\delta \right)}\left({\tau }_{*},{\zeta }_{*}\right)=f\left({\tau }_{*},{\zeta }_{*},P^{\left(\delta \right)}\right)$ ， $P^{\left(\delta \right)}\in {ℝ}^3$ 与 $F\left({\tau }_{*},{\zeta }_{*}\right)=f\left({\tau }_{*},{\zeta }_{*},P\right)$ 满足下述不等式

$\underset{\left({\tau }_{*},{\zeta }_{*}\right)\in D}{\sup }d\left(F^{\left(\delta \right)}\left({\tau }_{*},{\zeta }_{*}\right),F\left({\tau }_{*},{\zeta }_{*}\right)\right)\le {ϵ}^{*}\left(\delta \right)$ (9)

其中 ${ϵ}^{*}\left(\delta \right)$ 为正值函数， $\delta \in \left(0,\infty \right)$ ，且当 $\delta \to 0$ 时 ${ϵ}^{*}\left(\delta \right)\to 0$ 。

下面我们描述对集合 ${\mathcal{Z}}^a\left({\tau }_{i+1}\right)$ 的构造过程。首先，定义有限元素的近似集合 ${\mathcal{Z}}^a\left({\tau }_0\right)$ ，且 ${\mathcal{Z}}^a\left({\tau }_0\right)\subset {ℝ}^4\times \left[-{\alpha }_0,{\alpha }_0\right]\times \left[a,b\right]$ 满足

$d\left({\mathcal{Z}}^a\left({\tau }_0\right),\mathcal{Z}\left({\tau }_0\right)\right)=d\left({\mathcal{Z}}^a\left({\tau }_0\right),M\right)\le {\sigma }^{*}\left(\Delta \right)$ (10)

其中 ${\sigma }^{*}\left(\delta \right)$ 为正值函数， $\delta \in \left(0,\infty \right)$ ，且当 $\delta \to 0$ 时 ${\sigma }^{*}\left(\delta \right)\to 0$ 。

对于 ${\mathcal{Z}}^a\left({\tau }_{i+1}\right)$ $\left(i=\overline{0,N-1}\right)$，满足如下递推关系

${\mathcal{Z}}^a\left({\tau }_{i+1}\right)=Z^{\left(\Delta \right)}\left({\tau }_{i+1},{\tau }_i,{\mathcal{Z}}^a\left({\tau }_i\right)\right)$ (11)

由系统(4)与(5)满足的条件，对 ${\mathcal{Z}}^a\left({\tau }_{i+1}\right)$ ， $i=\overline{0,N-1}$ 也成立，与 [20] 估计相似

$d\left({\mathcal{Z}}^a\left({\tau }_i\right),\mathcal{Z}\left({\tau }_i\right)\right)\le {\text{e}}^{L\left({\tau }_i-{\tau }_0\right)}\left[{\sigma }^{*}\left(\Delta \right)+\left({\tau }_i-{\tau }_0\right)\left({ϵ}^{*}\left(\Delta \right)+{\omega }^{*}\left(\Delta \right)+LK\Delta \right)\right]$ ， (12)

其中 $K={\max }_{\left(t,\xi ,u\right)\in D\times P}\Vert f\left(t,\xi ,u\right)\Vert <+\infty$ 。满足

${\max }_{{\tau }_i\in \Gamma }d\left({\mathcal{Z}}^a\left({\tau }_i\right),\mathcal{Z}\left({\tau }_i\right)\right)\to 0$ ， $\Delta \to 0$ 。 (13)

因此， ${\mathcal{Z}}^a\left({\tau }_i\right)$ $\left(i=\overline{0,N}\right)$ 是积分漏斗 $\mathcal{Z}$ 在瞬时时刻 ${\tau }_i\in \Gamma$ $\left(i=\overline{0,N}\right)$ 对应 $\mathcal{Z}\left({\tau }_i\right)$ 的近似。定义 ${\mathcal{Z}}^a\left({\tau }_i\right)$ $\left(i=\overline{0,N}\right)$ 中元素个数为 $m\left({\mathcal{Z}}^a\left({\tau }_i\right)\right)$ ，由于随着i的增加， $m\left({\mathcal{Z}}^a\left({\tau }_i\right)\right)$ 会因为过大而无法进行有效计算，因此，我们必须对 ${\mathcal{Z}}^a\left({\tau }_i\right)$ 进行稀疏化(thin)处理。

下面我们将集合 ${\mathcal{Z}}^a\left({\tau }_i\right)$ 通过聚类的方法稀疏化得到 ${\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_i\right)$ 。

最大距离法(maxmin-distance)在聚类应用中得到了广泛的应用 [21] [21] 。首先，假设 $\bar{\mu }\left(\delta \right)$ 为正值函数， $\delta \in \left(0,\infty \right)$ ，且满足 $\delta \to 0$ 时 $\bar{\mu }\left(\delta \right)\to 0$ 。在集合 $\left\{\left({\tau }_i,{\zeta }_{*}\right),{\zeta }_{*}\in {\mathcal{Z}}^a\left({\tau }_i\right)\right\}$ $\left(i=\overline{0,N}\right)$ 中选取任意的 $\left({\tau }_i,{\zeta }_1\right)$ 作为第一个聚点。同时计算 ${\zeta }_1$ 与 $\zeta \in {\mathcal{Z}}^a\left({\tau }_i\right)$ 之间的欧氏距离

$d^{*}\left(\zeta ,{\zeta }_1\right)={\left[{\left(x-x_1\right)}^2+{\left(y-y_1\right)}^2+{\left(z-z_1\right)}^2+{\left(v-v_1\right)}^2+{\left(\alpha -{\alpha }_1\right)}^2+{\left(\beta -{\beta }_1\right)}^2\right]}^{\frac{1}{2}}$ ，

其中 ${\zeta }_1={\left[x_1,y_1,z_1,v_1,{\alpha }_1,{\beta }_1\right]}^{\text{T}}$ ， $\zeta ={\left[x,y,z,v,\alpha ,\beta \right]}^{\text{T}}\in {\mathcal{Z}}^a\left({\tau }_i\right)$ 。

选取满足与第一个聚点 ${\zeta }_1$ 之间的欧氏距离最大的 ${\zeta }_2$ ，记 $d^{*}\left({\zeta }_2,{\zeta }_1\right)=d_{max}^{*}\left({\tau }_i\right)$ 。接下来继续选取其他聚点，对于任意的 $\zeta \in {\mathcal{Z}}^a\left({\tau }_i\right)$ ，分别与前两个聚点 ${\zeta }_1$ ， ${\zeta }_2$ 之间的欧氏距离进行比较。假设 $d^{*}\left(\zeta ,{\zeta }_2\right)\le d^{*}\left(\zeta ,{\zeta }_1\right)$ ，令 $d^{*}\left(\zeta \right)=d^{*}\left(\zeta ,{\zeta }_2\right)$ 。若 $d^{*}\left(\zeta \right)\ge \bar{\mu }\left(\delta \right)d_{max}^{*}\left({\tau }_i\right)$ ，则令 $\zeta$ 为第三个聚点。由于 $f\left(t,\xi ,u\right)$ 有界连续，则存在常值 $d_h$ ，使 $d_{max}^{*}\left({\tau }_i\right)\le d_h$ 对 $i=\overline{0,N}$ 成立。令 $\mu \left(\delta \right)=\delta {\mu }^{*}\left(\delta \right)$ ，其中 ${\mu }^{*}\left(\delta \right)=\bar{\mu }\left(\delta \right)d_h$ 。其他的聚点按照上述条件选取，假设一共有p个聚点 $\left\{\left({\tau }_i,{\zeta }_1\right),\cdots ,\left({\tau }_i,{\zeta }_p\right)\right\}$ 。通过上述聚类过程，有限集 ${\mathcal{Z}}^a\left({\tau }_i\right)$ $\left(i=\overline{0,N}\right)$ 中的元素个数会减少，并且随着i的增加，对应稀疏化后的集合中元素个数会减少。

令 ${\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_0\right)=C^{\left(\Delta \right)}\left({\mathcal{Z}}^a\left({\tau }_0\right)\right)$ ，且

${\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_{i+1}\right)=C^{\left(\Delta \right)}\left(Z^{\left(\Delta \right)}\left({\tau }_{i+1},{\tau }_i,{\mathcal{R}}_{Z^a}\left({\tau }_i\right)\right)\right)$ ， $i=\overline{0,N-1}$ ， (14)

作为 ${\mathcal{Z}}^a\left({\tau }_i\right)$ $\left(i=\overline{0,N}\right)$ 稀疏化后的近似。由上述分析可知，

$d\left({\mathcal{Z}}^a\left({\tau }_0\right),{\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_0\right)\right)\le \mu \left(\Delta \right)$ 。 (15)

对于 ${\tau }_i\in \Gamma$ ， $i=\overline{1,N}$ ，根据文献 [20] ，有

$\begin{array}{c}d\left({\mathcal{Z}}^a\left({\tau }_1\right),{\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_1\right)\right)\le d\left(Z^{\left(\Delta \right)}\left({\tau }_1,{\tau }_0,{\mathcal{Z}}^a\left({\tau }_0\right)\right),Z^{\left(\Delta \right)}\left({\tau }_1,{\tau }_0,{\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_0\right)\right)\right)\\ +d\left(Z^{(\Delta )}\left({\tau }_1,{\tau }_0,{\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_0\right)\right),C^{\left(\Delta \right)}\left(Z^{\left(\Delta \right)}\left({\tau }_1,{\tau }_0,{\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_0\right)\right)\right)\right)\\ \le {\text{e}}^{L\Delta }d\left({\mathcal{Z}}^a\left({\tau }_0\right),{\mathcal{R}}_{Z^a}\left({\tau }_0\right)\right)+\mu \left(\Delta \right)\\ \le \left(1+{\text{e}}^{L\Delta }\right)\mu \left(\Delta \right)\end{array}$ ， (16)

$\begin{array}{c}d\left({\mathcal{Z}}^a\left({\tau }_2\right),{\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_2\right)\right)\le d\left(Z^{\left(\Delta \right)}\left({\tau }_2,{\tau }_1,{\mathcal{Z}}^a\left({\tau }_1\right)\right),Z^{\left(\Delta \right)}\left({\tau }_2,{\tau }_1,{\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_1\right)\right)\right)\\ +d\left(Z^{\left(\Delta \right)}\left({\tau }_2,{\tau }_1,{\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_1\right)\right),C^{\left(\Delta \right)}\left(Z^{\left(\Delta \right)}\left({\tau }_2,{\tau }_1,{\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_1\right)\right)\right)\right)\\ \le {\text{e}}^{L\Delta }d\left({\mathcal{Z}}^a\left({\tau }_1\right),{\mathcal{R}}_{Z^a}\left({\tau }_1\right)\right)+\mu \left(\Delta \right)\\ \le \left(1+{\text{e}}^{L\Delta }+{\text{e}}^{2L\Delta }\right)\mu \left(\Delta \right)\end{array}$ ， (17)

因此，

$d\left({\mathcal{Z}}^a\left({\tau }_i\right),{\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_i\right)\right)\le {\displaystyle \underset{q=0}{\overset{i}{\sum }}{\text{e}}^{qL\Delta }}\mu \left(\Delta \right)$ ， (18)

所以下面的估计是有效的

${\displaystyle \underset{q=0}{\overset{i}{\sum }}{\text{e}}^{qL\Delta }}\mu \left(\Delta \right)=\frac{{\text{e}}^{\left(i+1\right)L\Delta }-1}{{\text{e}}^{L\Delta }-1}\mu \left(\Delta \right)$ ， $i=\overline{0,N}$ ， (19)

假设r是常值， $\Delta =L^{-1}\ln r$ ， $1<r$ ，则

$\frac{{\text{e}}^{\left(i+1\right)L\Delta }-1}{{\text{e}}^{L\Delta }-1}\le \frac{r{\text{e}}^{L\left({\tau }_i-{\tau }_0\right)}}{L\Delta }$ ， $i=\overline{1,N}$ ， (20)

$d\left({\mathcal{Z}}^a\left({\tau }_i\right),{\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_i\right)\right)\le \frac{r}{L}{\text{e}}^{L\left({\tau }_i-{\tau }_0\right)}{\mu }^{*}\left(\Delta \right)$ ， $i=\overline{1,N}$ 。 (21)

由于 $\mathcal{W}\left(t_j\right)=\mathcal{Z}\left({\tau }_i\right)$ ， ${\tau }_i+t_j=t_0+\theta$ ， $i+j=N$ ， $i=\overline{0,N}$ ，并且近似集 ${\mathcal{W}}^a\left(t_j\right)={\mathcal{Z}}^a\left({\tau }_i\right)$ ，如下不等式成立

$\begin{array}{c}d\left(\mathcal{W}\left(t_j\right),{\mathcal{R}}_{{\mathcal{W}}^a}\left(t_j\right)\right)\le d\left(\mathcal{W}\left(t_j\right),{\mathcal{W}}^a\left(t_j\right)\right)+d\left({\mathcal{W}}^a\left(t_j\right),{\mathcal{R}}_{{\mathcal{W}}^a}\left(t_j\right)\right)\\ \le {\text{e}}^{L\left(\theta -t_j\right)}\left({\sigma }^{*}\left(\Delta \right)+\frac{r}{L}{\mu }^{*}\left(\Delta \right)+\left(\theta -t_j\right)\left({ϵ}^{*}\left(\Delta \right)+{\omega }^{*}\left(\Delta \right)+LK\Delta \right)\right)\end{array}$ ， $j=\overline{0,N}$ ， (22)

并且，有

${\max }_{t_j\in \Gamma }\left(\mathcal{W}\left(t_j\right),{\mathcal{R}}_{{\mathcal{W}}^a}\left(t_j\right)\right)\to 0$ ， $\Delta \to 0$ 。 (23)

3.2. 基于Euler方法构造容许控制求解可行路径

Euler方法是一种数值求解方法，适用于连续的运动方程。对于多无人机系统而言，每架无人机都有其运动方程，Euler方法能够有效地处理这些微分方程，提供对系统状态的准确估计。本节描述通过Euler方法构造容许控制的过程 [15] 。

首先，对于系统(5)，设 ${\zeta }^{\left(0\right)}=\zeta \left(t_0\right)$ ，

$\zeta \left(\tau \right)={\zeta }^{\left(0\right)}-\left(\tau -{\tau }_0\right)f\left(t_0+\theta -{\tau }_0,{\zeta }^{\left(0\right)},v^{\left(0\right)}\right)$ 。 (24)

对时间段 $\left[{\tau }_0,{\tau }_1\right]$ ，

$\zeta \left({\tau }_1\right)={\zeta }^{\left(0\right)}-\left({\tau }_1-{\tau }_0\right)f\left(t_0+\theta -{\tau }_0,{\zeta }^{\left(0\right)},v^{\left(0\right)}\right)$ ， (25)

令 ${\zeta }^{\left(1\right)}=\zeta \left({\tau }_1\right)$ ，

$\zeta \left({\tau }_2\right)={\zeta }^{\left(1\right)}-\left({\tau }_2-{\tau }_1\right)f\left(t_0+\theta -{\tau }_1,{\zeta }^{\left(1\right)},v^{\left(1\right)}\right)$ ， (26)

继续递归下去，得到

$\zeta \left({\tau }_N\right)={\zeta }^{\left(N-1\right)}-\left({\tau }_N-{\tau }_{N-1}\right)f\left(t_0+\theta -{\tau }_N,{\zeta }^{\left(N-1\right)},v^{\left(N-1\right)}\right)$ ， (27)

其中 ${\zeta }^{\left(i\right)}=\zeta \left({\tau }_i\right)$ ， $v^{\left(i\right)}\in P^{\left(\Delta \right)}$ ， $\Gamma =\left\{{\tau }_0=t_0,{\tau }_1,\cdots ,{\tau }_N=\theta \right\}$ ， $\Delta ={\tau }_{i+1}-{\tau }_i$ ， $i=\overline{0,N-1}$ 。

另一方面，由Taylor展式

$\zeta \left(\tau \right)=\zeta \left({\tau }_i\right)+\frac{\text{d}{\zeta }^{\left(i\right)}}{\text{d}t}\left(\tau -{\tau }_i\right)+\frac{{\text{d}}^2{\zeta }^{\left(i\right)}}{\text{d}{t}^2}\frac{{\left(\tau -{\tau }_i\right)}^2}{2!}+\cdots +\frac{{\text{d}}^{n+1}{\zeta }^{\left(i^{*}\right)}}{\text{d}{t}^{n+1}}\frac{{\tau }^{\left(n+1\right)}}{\left(n+1\right)!}$ ， (28)

其中 ${\zeta }^{\left(i^{*}\right)}=\zeta \left({\tau }_{i^{*}}\right)$ ， ${\tau }_{i^{*}}$ 介于 $\tau$ 与 ${\tau }_i$ 之间。在时间段 $\left[{\tau }_i,{\tau }_{i+1}\right]$ 上

$\zeta \left({\tau }_{i+1}\right)=\zeta \left({\tau }_i\right)+\frac{\text{d}{\zeta }^{\left(i\right)}}{\text{d}t}\left({\tau }_{i+1}-{\tau }_i\right)+O\left({\left({\tau }_{i+1}-{\tau }_i\right)}^2\right)=\zeta \left({\tau }_i\right)+\Delta \frac{\text{d}{\zeta }^{\left(i\right)}}{\text{d}t}+O\left({\Delta }^2\right)$ 。 (29)

在时间段 $\left[{\tau }_i,{\tau }_{i+1}\right]$ 上， $i=\overline{0,N-1}$ ，因为 ${\mathcal{R}}_{{\mathcal{W}}^a}\left(t_j\right)={\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_i\right)$ ， $i+j=N$ ， $i=\overline{0,N}$ ，所以对于集合 ${\mathcal{R}}_{{\mathcal{W}}^a}\left(t_0\right)$ 中的任意一点 $\xi \left(t_0\right)={\xi }^{\left(0\right)}$ ，存在 $\zeta \left(\tau \right)\left(\tau \in \left[t_0,\theta \right]\right)$ ，使得 $\zeta \left({\tau }_N\right)=\xi \left(t_0\right)$ 。由此，可以计算对应的 $\zeta \left({\tau }_i\right)\in {\mathcal{R}}_{{\mathcal{Z}}^a}\left({\tau }_i\right)$ ， $i=\overline{0,N}$ 。对于系统(4)，令 $u^{\left(j-1\right)}=v^{\left(i\right)}$ ，且 $\xi \left(t_j\right)=\zeta \left({\tau }_i\right)$ ， $t_j+{\tau }_i=t_0+\theta$ ，其中 $i+j=N$ ，记录得到的控制 $u^{*}\left(t\right)$ ，其中

$u^{*}\left(t\right)=u^{\left(j-1\right)}=v^{\left(i\right)}$ ， $t\in \left[t_{j-1},t_j\right]$ ， $i+j=N$ ， $j=\overline{1,N}$ 。 (30)

对于系统(4)，有

${\xi }^{\left(j\right)}={\xi }^{\left(j-1\right)}+\Delta f\left(t_j,{\xi }^{\left(j\right)},u^{\left(j-1\right)}\right)$ ， (31)

假设

${\hat{\xi }}^{\left(j\right)}={\hat{\xi }}^{\left(j-1\right)}+\Delta f\left(t_{j-1},{\hat{\xi }}^{\left(j-1\right)},u^{\left(j-1\right)}\right)$ 。 (32)

令 ${\rho }_j=\Vert {\hat{\xi }}^{\left(j\right)}-{\xi }^{\left(j\right)}\Vert$ ， $j=\overline{0,N}$ 。由于 $\xi \left(t_0\right)={\xi }^{\left(0\right)}\in {\mathcal{R}}_{{\mathcal{W}}^a}\left(t_0\right)$ ,从初始状态 ${\xi }^{*}\left(t_0\right)={\xi }^{\left(0\right)}$ 出发，通过控制 $u^{*}\left(t\right)$ 构造可行路径 ${\xi }^{*}\left(t\right)$ ，其中

${\xi }^{*}\left(t\right)=\xi \left(t_0\right)+{\displaystyle {\int }_{t_0}^{t}f}\left(s,{\xi }^{*}\left(s\right),u^{*}\left(s\right)\right)\text{d}s$ 。 (33)

与 [15] 计算类似，

$\begin{array}{c}\rho \left({\xi }^{*}\left(t_N\right),M\right)=\rho \left({\xi }^{*}\left(t_N\right),\hat{\xi }\left(t_N\right)\right)+\rho \left(\hat{\xi }\left(t_N\right),M\right)\\ \le \Vert {\xi }^{*}\left(t_N\right)-\xi \left(t_N\right)\Vert +\Vert \hat{\xi }\left(t_N\right)-\xi \left(t_N\right)\Vert +\rho \left(\xi \left(t_N\right),M\right)\\ <2{\text{e}}^{L\left(\theta -t_0\right)}\left(K\Delta +\frac{1}{L}{\omega }^{*}\left(\Delta \right)\right)+{\sigma }^{*}\left(\Delta \right)+{\mu }^{*}\left(\Delta \right)\end{array}$ (34)

定理1存在 $\epsilon \in \left(0,+\infty \right)$ ，对上述时间分割 $\Gamma$ ，若 $0<\Delta \left(\Gamma \right)\le \frac{1}{L}$ ，有

$2{\text{e}}^{L\left(\theta -t_0\right)}\left(K\Delta +\frac{1}{L}{\omega }^{*}\left(\Delta \right)\right)+{\sigma }^{*}\left(\Delta \right)+{\mu }^{*}\left(\Delta \right)\le \epsilon$ ， (35)

则对任意 ${\xi }^{\left(0\right)}\in {\mathcal{R}}_{{\mathcal{W}}^a}\left(t_0\right)$ ，可以构造分段常值控制 $u^{*}\left(t\right)=u^{\left(j-1\right)}$ ， $t\in \left[t_{j-1},t_j\right]$ ， $j=\overline{1,N}$ ，形成运动轨迹 ${\xi }^{*}\left(t\right)$ ，使得 ${\xi }^{*}\left(t_0\right)={\xi }^{\left(0\right)}$ 且 ${\xi }^{*}\left(\theta \right)\in M$ ，即每架无人机能够同时到达三维空间中的目标区域 $T_{*}$ 。

3.3. 障碍环境中多无人机航路规划

在上一节中，我们成功求解了单架无人机的可行运动轨迹及其相应的控制方案。事实上，多架无人机同时到达与其求解过程一致，即同时可以求出无人机编队中每架无人机的可行运动轨迹与容许控制。接下来，我们将探讨三维空间中多架无人机的避碰模型。为了简化模型，我们将每架无人机视为球体，将障碍物建模为直圆柱(见图1)。

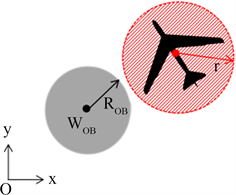
Figure 1. Model of the UAV and straight cylinder obstacles

图1. 无人机与障碍物模型

由定理1，假设对第i架无人机的任意初始状态 ${\xi }_i\left(t_0\right)\in {\mathcal{R}}_{{\mathcal{W}}_i^a}\left(t_0\right)$ ， $i=\overline{1,N}$ ，容许控制 ${\bar{u}}_i\left(t\right)=u^{\left(j-1\right)}$ ， $t\in \left[t_{j-1},t_j\right]$ ， $j=\overline{1,N}$ ，形成运动 $\left\{{\bar{\xi }}_i\left(t_j\right):{\xi }_i^{*}\left(t_0\right)={\xi }_i\left(t_0\right)\in {\mathcal{R}}_{{\mathcal{W}}_i^a}\left(t_0\right),t_j\in \Gamma ,j=\overline{0,N}\right\}$ 。那么，无人机与障碍物碰撞区域可以描述为

$\psi =\left\{{\left(x_i,y_i,z_i\right)}^{\text{T}}:{\left(x_i-w_{OB}\right)}^2+{\left(y_i-w_{OB}\right)}^2\le R^2+r^2\right\}$ ， (36)

无人机 $i_1$ 与无人机 $i_2$ 之间的碰撞区域为，

$\chi =\left\{{\left(x_{i_1},y_{i_1},z_{i_1}\right)}^{\text{T}},{\left(x_{i_2},y_{i_2},z_{i_2}\right)}^{\text{T}}:{\left(x_{i_1}-x_{i_2}\right)}^{\text{2}}+{\left(y_{i_1}-y_{i_2}\right)}^2+{\left(z_{i_1}-z_{i_2}\right)}^2\le 2r^2\right\}$ 。(37)

由此，可以通过上述条件判断无人机是否与障碍物或其他无人机之间发生碰撞，进而选出可以安全飞行且同时到达目标区域的无人机飞行路线。

定理2对第i架无人机的任意初始状态 ${\xi }_i\left(t_0\right)\in {\mathcal{R}}_{{\mathcal{W}}_i^a}\left(t_0\right)$ ， $i=\overline{1,I}$ ，存在满足定理1条件的容许控制 ${\bar{u}}_i\left(t\right)$ ，形成运动轨迹 ${\bar{\xi }}_i\left(t\right)$ $\left(t\in \left[t_0,\theta \right]\right)$，使 $t=\theta$ 时无人机能够躲避上述碰撞区域并安全到达 $T_{*}$ 即 ${\bar{\xi }}_i\left(\theta \right)\in M$ 。

4. 仿真与分析

为了验证理论结果的正确性，本节对第二节和第三节中求解的每架无人机的可解集和安全到达轨迹进行了仿真验证。

考虑在有限时间段 $t\in \left[0,\theta \right]$ 上的每架无人机控制系统(4)，且在 $t=\theta$ 时每架无人机安全到达 $T_{*}$ 。由于无人机的实际控制输入受限于无人机机动性能，且过大的控制输入可能会导致机器受损或寿命下降[23]。设无人机的控制输入限制在一定范围内，

$0\le u_x\le u_{\max }$ ， $0\le u_y\le u_{\max }$ ， $0\le u_z\le u_{\max }$

其中 $u_{\max }$ 为控制输入的最大值。

设置控制系统的参数 $m=1$ ， $L^0=10$ ， $D=6$ ， $g=9.80$ ， $\theta =30$ ，且时间段 $\left[0,30\right]$ 上的分割 $\Gamma$ 的步长 $\Delta =0.5$ ， $t_0=0$ ， $t_N=30$ ，且控制输入 $u_x$ ， $u_y$ ， $u_z$ 从步长为0.2有限值集 $\left[0,1\right]$ 中取，即 $u_{\max }=1$ 。假设每架无人机要到达的目标为 $T_{*}={\left(101,101,98\right)}^{\text{T}}$ ， $M={\left(101,101,98,\text{30,}\frac{\pi }{3}\text{,}\frac{\pi }{3}\right)}^{\text{T}}$ ，为简便计算，在靠近目标地点的小邻域内不考虑无人机自身安全半径的影响。设 $t=0$ 时，对UAV₁，UAV₂，UAV₃分别有：

${\xi }_1^0={\left(127.55,-37.06,-285.00,7.35,-0.02,3.68\right)}^{\text{T}}$ ，

${\xi }_2^0={\left(126.38,-100.90,-356.16,8.35,0.36,2.99\right)}^{\text{T}}$ ，

${\xi }_3^0={\left(-127.75,-295.21,-694.41,30,1.05,1.05\right)}^{\text{T}}$ 。

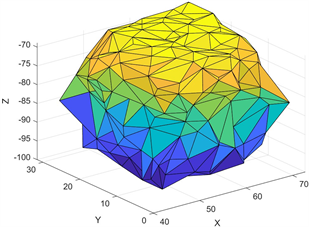
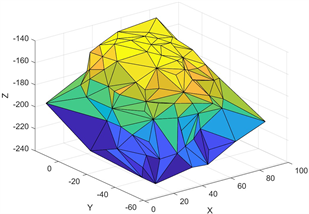
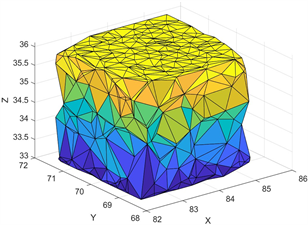
Figure 2. Projections of ${\mathcal{R}}_{{\mathcal{W}}_1^a}$ onto ${ℝ}_{1,2,3}$ for $t=17.5,t=22.5,t=27.5$

图2. 无人机与障碍物模型对于 $t=17.5,t=22.5,t=27.5$ ， ${\mathcal{R}}_{{\mathcal{W}}_1^a}$ 在 ${ℝ}_{1,2,3}$ 的投影示意图

以UAV₁为例，可以得到 ${\mathcal{R}}_{{\mathcal{W}}_1^a}$ 投影到 ${ℝ}_{1,2,3}$ 上的图像，如图2所示。假设UAV₁，UAV₂，UAV₃分别从各自的初始位置出发，在控制作用下 $t=30$ 时同时到达目标区域 $T_{*}$ ，对应的轨迹由图3所示。

以UAV₁为例，其对应的控制 $u^{*}\left(t\right)$ ， $t\in \left[0,30\right]$ 可由图4表示。

假设每架无人机半径 $r=0.5$ ，每个障碍物 $R_{OB}=3$ ，在xoy平面 $w_{OB}$ 的坐标分别为 $\left(90,-10\right)$ 。

图5表明，在可行路径中UAV₁可以选择图示的轨迹安全到达目标区域，对应的控制如图6所示，确保了UAV₁，UAV₂与UAV₃同时到达目标区域 $T_{*}$ ，其中红色的轨迹表示不被选择的UAV₁运行轨迹。

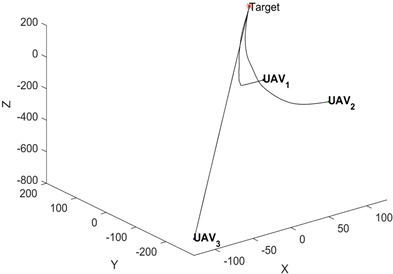
Figure 3. Projection of the motion ${\xi }_i^{*}\left(t\right)$ onto ${ℝ}_{1,2,3}$ for $t\in \left[0,30\right]$ , $i=\overline{1,3}$

图3. 运动轨迹 ${\xi }_i^{*}\left(t\right)$ ， $t\in \left[0,30\right]$ ， $i=\overline{1,3}$ 在 ${ℝ}_{1,2,3}$ 的投影示意图

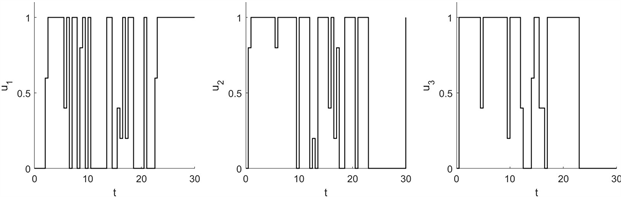
Figure 4. Control $u^{*}\left(t\right)$ of UAV₁, $t\in \left[0,30\right]$

图4. UAV₁控制 $u^{*}\left(t\right)$ ， $t\in \left[0,30\right]$ 示意图

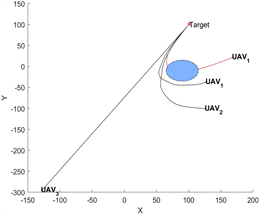
Figure 5. Projection of the motion $\overline{{\xi }_i}\left(t\right)$ onto ${ℝ}_{1,2,3}$ for UAV₁, UAV₂, UAV₃ with straight cylinder obstacles, $i=\overline{1,3}$

图5. UAV₁，UAV₂，UAV₃的安全轨迹 $\overline{{\xi }_i}\left(t\right)$ 在 ${ℝ}_{1,2,3}$ 的投影示意图

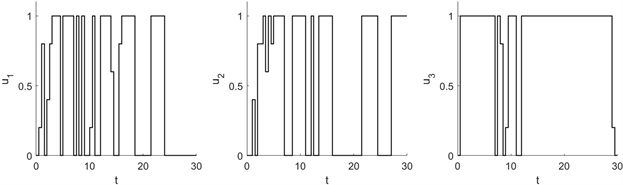
Figure 6. Control $\bar{u}\left(t\right)$ of UAV₁, $t\in \left[0,30\right]$

图6. UAV₁控制 $\bar{u}\left(t\right)$ ， $t\in \left[0,30\right]$ 示意图

5. 结论

本文研究了在障碍情境下多架无人机同时安全到达给定目标区域的问题，并提出了一个完整的求解框架。通过将此问题转化为目标逼近问题，我们在Ushakov算法的基础上，构建了基于距离聚类的Euler算法，以求解每架无人机系统对应的可解集，并对求解过程中的估计进行误差分析，从而求解出安全路径，以避免无人机与无人机及无人机与障碍物之间的碰撞。对于在数值仿真中，我们得到了多架无人机的运动轨迹，仿真结果表明，多架无人机可以在障碍情境中避免碰撞并安全到达给定目标区域。

本文对多架无人机同时安全到达目标区域的问题进行了研究，并取得了一定的研究成果。但是，还存在以下问题需要进一步研究和完善：本文主要针对每架无人机分别求解可解集，未考虑无人机之间的交互与信息传输。未来的研究可以扩展到考虑多架无人机之间的协同控制和通信，以实现更高效、更安全的无人机集群任务。在这种情景下，需要开发新的算法，以考虑无人机之间的相互影响，并将其纳入计算过程中。另外，多无人机系统需要具备智能决策机制，以在动态环境中做出实时的、协同的飞行决策。这可能涉及集体智能算法、机器学习和人工智能技术的应用。因此，需要通过更多的试验，分析实验数据，对控制参数进行修正，改进算法，为实际应用奠定基础。总体而言，利用目标逼近算法解决多无人机同时到达问题不仅有望在各领域提升协同效率，还具有潜在的社会、经济和安全价值。然而，需要在实际应用中不断验证和优化算法，以确保其在复杂环境下的稳健性和可靠性。