“双减”政策下中小学校外培训市场主体四方演化博弈分析

Analysis of the Four-Party Evolutionary Game of Primary and Secondary School Out-of-School Training Market Entities under the “Double Reduction” Policy

摘要: 教育是国之大计。我国中小学教育阶段的学业负担过重问题一直受到关注，教育部针对此问题发布了多项减负政策。2021年的“双减”政策，将校外培训机构的纠偏推向了公众视野。然而，“双减”政策的目标更广泛，旨在建设高质量的教育体系，构建优良的教育生态，落实立德树人的任务。本文基于演化博弈理论，构建了一个包含地方政府、学校、培训机构和家庭等四个主体的策略演化模型。结果表明，要实现“双减”的目标，需要降低地方政府监管成本并保持政策力度，引导培训机构转型，培养健康的教育文化，以及降低学校提质的成本，探索社会评价作为评估学校的依据。

Abstract: Education is extremely important for a nation. The issue of excessive academic burden in China’s primary and secondary education stages has always been a focus of attention, and multiple burden-reducing policies have been issued by the Ministry of Education in response. The “Double Reduction” policy of 2021 brought the rectification of extracurricular training institutions into public view. However, the objectives of the “Double Reduction” policy are broader, aiming to build a high-quality education system, establish a good educational ecosystem, and implement the fundamental task of moral education. This paper, based on evolutionary game theory, constructs a strategy evolution model that includes four main bodies: local governments, schools, training institutions, and families. The results show that to achieve the goals of the “Double Reduction” policy, it is necessary to reduce the regulatory costs of local governments while maintaining policy intensity, guide training institutions in their transformation, cultivate a healthy education culture, and reduce the cost of quality improvement for schools, exploring social evaluation as an important basis for the administrative education department’s assessment of schools.

1. 引言

教育阶段学生负担过重是我国现阶段教育事业一大顽疾。针对义务教育阶段的减负问题，教育部已有一系列的政策和行动，但收效一直收效不明显 [1] 。“双减”政策从2017年实施至今，已取得了较为显著的效果 [2] 。但义务教育阶段学业的负担治理和校外培训治理是一个系统工程，要想真正达成“双减”政策的内在目标，核心在于政策的长效落实 [3] 。

2. 研究背景

随着社会的进一步发展，公众对教育的需求呈多元化和个性化的趋势。这使得学校提供的教育内容无法全面满足家长对孩子教育的期待和需求。许多家庭选择对子女进行扩展性的教育投资，以期通过教育实现社会阶层的流动 [4] 。久而久之导致了课外培训机构的过度发展。这不仅增加了家长和学生的教育负担，也导致了教育需求的过度和异化和区域、群体之间的教育公平问题 [5] 。2021年7月，中共中央办公厅和国务院办公厅联合发布了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》(简称“双减”)。这一政策是推进我国中小学生减负工作、优化教育生态的重要举措。

实际上，早在1955年，义务教育阶段的学生减负问题就已经被教育部关注并采取了一系列的行动。进入21世纪后，在2000年，教育部发布了《关于小学生减轻负担的紧急通知》，并在随后的二十多年中，陆续推出了一系列减负政策。这次的“双减”政策不仅体现了国家对中小学“减负”的重视和决心，也揭示了多次减负政策后学生的课业负担仍然沉重的实际问题。一些学者指出，针对义务教育阶段的减负工作有政策高频次周期短的特点，在执行方面的“疲劳症”和“厌烦症”使得政策效果收效不明显[1]。还有学者将义务制教育的学业负担问题和校外培训问题比喻为“不断变异的教育病毒”，认为短期的、应急的、非长效的政策“抗毒”只能治理表象，有时反而会使“病毒”增殖和变本加厉 [6] 。

针对本次“双减”政策执行过程中出现的问题，众多学者从教育生态系统的不同角度进行了讨论和研究。杨燕 [7] 在从政策执行实践的综合调查出发，说明了“双减”政策存在“形式”上完成的现象，执行中可能出现素质教育20年改革老路的风险。张冰 [8] 等人的研究发现，义务教育阶段的减负政策有三个变迁特征：制定和颁布的主体日益权威化，从提高教育质量入手以期从根源上减负，以及执行主体明确、多方合作减负。豆建荣 [9] 则从村小的微观角度，指出了落实“双减”政策的难度；黄志豪 [10] 等指出再“双减”政策下青少年体育培训发展也不像想象中那般迎来巨大机遇；卢迎丽 [11] 等结合“双减”政策对学校的内在要求，说明学校变革的困局；张茂聪 [12] 等则分析了引入社会组织参与校外培训机构治理的可能和机制探索；肖芳飞 [13] 等则分析了地方政府在落实“双减”政策时可能存在的偏差并提供了纠错建议。

我们可以看到，“双减”政策影响地方教育行政部门、学校、学生、家长及校外培训机构等多组利益相关群体 [14] ，但关于他们间互动关系的研究较少。本文以义务教育阶段减负的长效落实为主题，采用演化博弈理论，将地方政府、学校、校外培训机构和家庭定义为博弈主体，分析各方的行为策略选择及关键影响因素。在此基础上，以学校提质、家庭尊重教育规律、校外机构做素质拓展补充为目标，提出长期策略启示，旨在为“双减”政策的实施提供参考建议。

3. 问题描述和模型建构

3.1. 问题描述

本研究关注由地方政府、学校、培训机构和家庭组成的教育生态系统。如图1所示，这四个主体之间存在着紧密的逻辑关系。

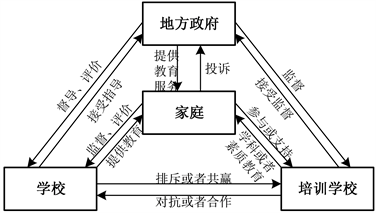
Figure 1. Logical relationships in the four-player game model

图1. 四方博弈模型逻辑关系

地方政府是“双减”政策的执行者，通过行政措施将政策目标导入其他三个主体。然而，地方政府的行为受其双重身份——“政治人”和“经济人”的影响 [15] 。执行政策时，地方政府需遵循上级部门指导，考虑地方条件对政策执行的限制，争取教育资源和社会支持，同时考虑上级行政部门的政策愿景 [16] 。因此，地方政府既有积极参与政策落地的一面，也存在因信息不对成、政策解读偏差而偏离“双减”目标的行动。例如，一些省教育厅在政策颁布后，以降低考试难度的方式“实现”减负，这不能满足教育需求，也背离了“双减”的核心目标。

学校是“双减”政策实施过程的核心参与者，其办学方针和具体落实主要受地方政府(教育行政部门)主导，同时，也受到社会监督和家长对升学率的关注压力。学校有提升教学质量、提升课后服务水平等符合“双减”政策的动机，因为这可以增强学校在本地的教育生态优势。然而学校也可能因为上级监管存在信息不对称或者默认某些政策变通行为采取变通性执行、选择性执行等偏离政策愿景的局部理性行动。

然后是培训机构。培训机构是“双减”政策执行过程中受影响最为深刻的参与者。在中小学教育生态中，培训机构一方面可以满足教育多样化、个性化的公众需求，另一方面利用家长焦虑心理推广学科内容，引导学校教育走向“异化”。本次“双减”政策用行政手段迫使学科培训机构“退场”，但一些机构“旧酒装新瓶”，以住家教师、学科研学、素质拓展等形式继续之前的学科教学和学科内容补习。虽对上述违规行为的举报和处理屡见报端，但更多的却是被家长所认可、支持和掩藏。在杨小敏 [17] 等人的文章中指出，在“双减”严查严打的形势下，教育资本以“地下培训机构”的形式与家长需求重新结合，将之前的校外学科补习市场“化整为零”。

最后，家庭，包括家长和学生，是政策实施的主要利益方和参与者。政策期望家长全面参与孩子的成长，设定合理的发展期望，增强与孩子的交流，引导良好的学习生活习惯，尊重人的自然发展规律。然而，当前就业压力、社会保障体系不完善、优质教育资源有限，职业教育社会认可度需提高，学生面临显著的升学压力。因此，家长面临长期目标与短期个人发展需求的矛盾，过度关注孩子是否能进入知名学校，忽视孩子的兴趣和适应性。在评估“双减”政策时，家长主要考虑其是否能帮助孩子在学业竞争中突出。如果不能，他们可能会增加孩子的作业量或请家教。据统计，实施“双减”后，19.1%的家长会额外为孩子布置作业。只有当家长理解并配合“双减”政策的目的，加强家庭教育，尊重教育规律，才会减少参与校外培训的行为。

3.2. 模型构造

为了构建“双减”政策下各利益主体间的博弈模型，研究政策落地策略，做出如下假设。

假设1 选择地方政府、学校、培训机构、家庭四方作为博弈主体。地方政府以x的概率积极落实“双减”政策，称为“积极监督”，包括监督培训机构、督促学校提升办学质量、构建公共学习平台等，以 $1-x$ 的概率“消极监管”；学校积极提升自身教育教学质量的概率为y，保持现状的概率为 $1-y$ ；培训机构积极响应“双减”政策号召，积极探索转型的概率为z，称之为“积极转型”；而培训机构利用各种途径，继续现有培训模式的概率为 $1-z$ ，称之为“转为地下”；家庭不参加校外学科培训概率为w，积极参加校外学科培训概率为 $1-w$ ； $x,y,z,w\in \left[0,1\right]$ 。当我们将视角扩大到整个社会群体时，每个策略的选择概率可以理解为在群体中选择特定策略的博弈主体的比例。我们假设所有博弈的主体都是风险中性的，各主体的目标都是追求自身利益的最大化。

假设2 地方政府积极监管时，会得到上级部门肯定，更容易完成业绩，得到民众的信赖，记为收益R₁；严格监管需要人力物力，为积极监管成本C₁；对学校的政策和经费支持记为c；地方政府积极构建和推广公共服务平台等对家庭有直接的积极影响R₂；学校有诸如应付检查、参与构建线上平台等压力，记为C₂；严格监管会处罚转为地下的培训机构，记为P₁，对不提升质量的学校进行处罚P₂；政府消极监管时，其自身监管成本减少，令 $\beta$ 为其成本系数，同时，转为地下的机构宣传成本减少，令 $\alpha$ 为成本系数，显然， $\beta <1$ ， $\alpha <1$ .

假设3 学校积极提升质量，会有一定的成本，记为C₃，对积极转型的课外培训和学科补习机构产生积极影响R₃，对转为地下的机构有消极影响P₃，对家庭和政府有积极影响记为R₄、R₅。学校不提升质量时，对消极监管的政府有负面影响P₄，不参加学科培训的家庭对其有负面评价P₅，不参加学科培训的家庭的负面影响记为P₆。

假设4 培训机构积极转型的探索成本记为C₄，对学校带来积极影响R₆，对家庭带来积极影响R₇；若培训机构转为地下，需要的宣传成本C₅，对政府有负面影响P₇。

假设5 家庭积极参加学科培训时，不转型机构能提供的积极影响记为R₈，积极转型机构对其影响减少，令 $\gamma$ 为影响系数， $\gamma <1$ ；积极参加学科培训的家庭的花费转移至转为地下的培训机构，记为S₂；不参加学科培训的家庭，花费由家庭转移至积极转型的培训机构记为S₃。

综上，四方博弈支付矩阵见表1和表2。

Table 1. The payoff matrix of the four-player game under family cooperation policy and without participation in extracurricular subject training

表1. 家庭配合政策、不参加校外学科培训时四方博弈收益矩阵

注：自上而下依次是地方政府、学校、培训机构和家庭的收益。

Table 2. The payoff matrix of the four-player game when the family does not cooperate with the policy and actively participates in extracurricular subject training

表2. 家庭不配合政策、积极参加校外学科培训时四方博弈收益矩阵

注：自上而下依次是地方政府、学校、培训机构和家庭的收益。

4. 各博弈主体策略稳定性分析

4.1. 地方政府策略选择的稳定性分析

地方政府选择“严格监管”和“消极监管”的期望收益分别为：

$E_{11}=P_1-C_1-P_7-S_1-z{P}_1+z{P}_7+y{R}_5$ ；

$E_{12}=y{P}_4-P_7-\beta C_1-P_4+z{P}_7+y{R}_5$ ；

因此，地方政府的平均收益为：

$\overline{E_1}=x{E}_{11}+\left(1-x\right)E_{12}$

地方政府的复制动态方程为：

$F\left(x\right)=\frac{\text{d}x}{\text{d}t}=x\left(E_{11}-\overline{E_1}\right)=x\left(x-1\right)\left(C_1-P_1-P_4-R_1+S_1-\beta C_1+y{P}_4+z{P}_1\right)$

接下来，我们讨论学校“提升教学质量”概率y的变化对地方政府的策略选择的影响。令 $y_0=\frac{P_1-C_1+P_4+R_1-S_1+\beta C_1-z{P}_1}{P_4}$ 可知：

1) 当 $y=y_0$ 时， $F\left(x\right)\equiv 0$ ，因此任意 $x\in \left[0,1\right]$ 均为稳定点；

2) 当 $y\ne y_0$ 时，由 $F\left(x\right)=0$ ，可以推出 $x=1$ 或 $x=0$ ，即地方政府“积极监管”或者“消极监管”都是稳定策略。

引理1当 $0<y<y_0$ 时，地方政府演化稳定策略为 $x=1$ ；当 $y_0<y<1$ 时，地方政府演化稳定策略为 $x=0$ 。

证明：对 $F\left(x\right)$ 关于变量x求一阶偏导，可得

$\frac{\text{d}F\left(x\right)}{\text{d}x}=\left(2x-1\right)\left(C_1-P_1-P_4-R_1+S_1-\beta C_1+y{P}_4+z{P}_1\right)$

由微分方程稳定性定理可知 [18] ，当地方政府选择“积极监管”策略的概率x满足： $F\left(x\right)=0$ 且 $\frac{\text{d}F\left(x\right)}{\text{d}x}<0$ 时，x为地方政府策略选择的演化稳定点。因此，当 $0<y<y_0$ 时，由 ${F\left(x\right)|}_{x=1}=0$ ， ${\frac{\text{d}F\left(x\right)}{\text{d}x}|}_{x=1}<0$ ，可知 $x=1$ 为演化稳定点，表明当学校选择“积极提升质量”策略的概率低于y₀时，地方政府最终选择“积极监管”策略。当 $y_0<y<1$ 时，由 ${F\left(x\right)|}_{x=0}=0$ ， ${\frac{\text{d}F\left(x\right)}{\text{d}x}|}_{x=0}<0$ ，可知 $x=0$ 为演化稳定点，表明当学校选择“积极提升质量”策略的概率高于y₀时，地方政府最终的策略选择会落在“消极监管”。

命题1地方政府严格监管时，对转为地下的机构的处罚、学校不提升质量时对不监管的地方政府的负面评价、政府自身的收益、地方政府不严格监管时的成本系数增加时，地方政府大概率会选择“积极监管”。

证明：地方政府策略选择的相位图如图2。图中的空间被曲面 $y=y_0$ 划分位I和II两个部分，其体积记为 ${\text{V}}_{x_1}$ 和 ${\text{V}}_{x_0}$ ，分别表示地方政府选择“积极监管”策略的概率和“消极监管”策略的概率。空间I是满足 $0<y<y_0$ 的初始策略集，由引理1可知，当地方政府初始状态位于空间I时，地方政府最终会选择“积极监管”策略。上面的空间II是满足 $y_0<y<1$ 的初始策略集，由引理1可知，当地方政府初始状态位于空间II时，最终，地方政府可能会选择“消极监管”策略。而在其他变量保持不变的情况下，随着 $P_1,P_4,R_1,\beta$ 增大，y₀将会增大，导致空间I增大，此时地方政府选择“积极监管”的概率增大。另一方面，S₁，C₁增大，y₀将会减小，导致空间II增大，此时地方政府选择“消极监管”的概率增大。

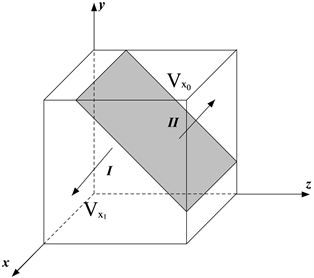
Figure 2. The phase diagram of local government policy choices

图2. 地方政府策略选择的相位图

4.2. 学校策略选择的稳定性分析

学校选择“提升教育教学质量”和“不提升教学质量”的期望收益分别为：

$E_{21}=x{S}_1-x{C}_2-C_3+z{R}_6$

$E_{22}=x{S}_1-w{P}_5-x{P}_2-x{C}_2+z{R}_6$

因此，学校的平均收益为：

$\overline{E_2}=x{E}_{21}+\left(1-x\right)E_{22}$

相应地，学校的复制动态方程为：

$G\left(y\right)=y\left(E_{21}-\overline{E_2}\right)=-y\left(y-1\right)\left(w{P}_5-C_3+x{P}_2\right)$

接下来，我们讨论家庭“不参加校外学科培训”概率w的变化对学校策略选择的影响。令 $w_0=\frac{C_3-x{P}_2}{P_5}$ ，可知：

1) 当 $w=w_0$ 时， $F\left(y\right)\equiv 0$ ，因此任意 $y\in \left[0,1\right]$ 均为稳定点；

2) 当 $w\ne w_0$ 时，由 $F\left(y\right)=0$ ，可以推出 $y=1$ 或 $y=0$ ，即学校“积极提升质量”或者“不提升质量”都是稳定策略。

引理2当 $0<w<w_0$ 时，学校演化稳定策略为 $y=0$ ；当 $w_0<w<1$ 时，学校演化稳定策略为 $y=1$ 。

证明：对 $G\left(y\right)$ 关于变量y求一阶偏导，可得

$\frac{\text{d}G\left(y\right)}{\text{d}y}=-\left(2y-1\right)\left(w{P}_5-C_3+x{P}_2\right)$

依据微分方程稳定性定理，当学校选择“积极提升质量”策略的概率y满足： $G\left(y\right)=0$ 且 $\frac{\text{d}G\left(y\right)}{\text{d}y}<0$ 时，y为学校策略选择的演化稳定点。因此，当 $0<w<w_0$ 时，由 ${G\left(y\right)|}_{y=0}=0$ ， ${\frac{\text{d}G\left(y\right)}{\text{d}y}|}_{y=0}<0$ ，可知 $y=0$ 为演化稳定点，表明当家庭选择“不参加校外学科培训”策略低于w₀时，学校最终选择“不提升质量”策略。当 $w_0<w<1$ 时，由 ${G\left(y\right)|}_{y=1}=0$ ， ${\frac{\text{d}G\left(y\right)}{\text{d}y}|}_{y=1}<0$ ，可知 $y=1$ 为演化稳定点，表明当家庭选择“不参加校外学科培训”策略高于w₀时，学校最终选择“积极提升质量”策略。

命题2当学校提升质量成本增加时，学校“不提升质量”的概率会有所增加。

证明：学校策略选择的相位图如图3。图中的空间被曲面 $w=w_0$ 划分位I和II两个部分，其体积记为 ${\text{V}}_{y_1}$ 和 ${\text{V}}_{y_0}$ ，分别表示学校选择“积极提升质量”策略的概率和“不提升质量”策略的概率。空间I是满足 $0<w<w_0$ 的初始策略集，由引理2可知，当学校初始状态位于空间II时，学校最终会选择“不提升质量”策略。上面的空间I是满足 $w_0<w<1$ 的初始策略集，由引理2可知，当学校初始状态位于空间I时，政府最终会选择“积极提升质量”策略。于此同时，在其他变量不变的条件下，随着C₃增大，w₀将会增大，导致空间II增大，此时政府选择“不提升质量”的概率增大。另一方面，P₂增大，w₀将会减小，导致空间I的扩大，进而使得政府选择“积极提升质量”策略的概率增大。

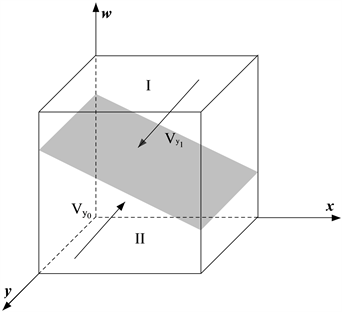
Figure 3. The phase diagram of school policy choices

图3. 学校策略选择的相位图

4.3. 培训机构策略选择的稳定性分析

培训机构选择“积极转型”策略和“转为地下”策略的期望收益分别如下：

$E_{31}=w{S}_3-y{P}_3-C_4+y{R}_3+yw{P}_3$

$E_{32}=S_2-\alpha C_5-x{C}_5-x{P}_1-w{S}_2+\alpha x{C}_5-yw{P}_3$

因此，培训机构的平均收益为：

$\overline{E_3}=z{E}_{31}+\left(1-z\right)E_{32}$

相应地，培训机构的复制动态方程为：

$H\left(z\right)=z\left(E_{31}-\overline{E_3}\right)=-z\left(z-1\right)\left(\alpha C_5-S_2-C_4+x{C}_5+x{P}_1-y{P}_3+w{S}_2+w{S}_3+y{R}_3-\alpha x{C}_5+2yw{P}_3\right)$

接下来，我们讨论家庭“不积极参加校外学科补习”概率w的变化对机构策略选择的影响。令

$w_1=\frac{C_4+S_2-\alpha C_5-x{C}_5-x{P}_1+y{P}_3-y{R}_3+\alpha x{C}_5}{S_2+S_3+2y{P}_3}$ ，

可知：

1) 当 $w=w_1$ 时， $H\left(z\right)\equiv 0$ ，因此任意 $z\in \left[0,1\right]$ 均为稳定点；

2) 当 $w\ne w_1$ 时，由 $H\left(z\right)=0$ ，可以推出 $z=1$ 或 $z=0$ ，即培训机构“积极转型”或者“转为地下”都是稳定策略。

引理3当 $0<w<w_1$ 时，培训机构演化稳定策略为 $z=0$ ；当 $w_1<w<1$ 时，培训机构演化稳定策略为 $z=1$ 。

证明：对 $H\left(z\right)$ 关于变量z求一阶偏导，可得

$\frac{\text{d}H\left(z\right)}{\text{d}z}=-\left(2z-1\right)\left(\alpha C_5-S_2-C_4+x{C}_5+x{P}_1-y{P}_3+w{S}_2+w{S}_3+y{R}_3-\alpha x{C}_5+2yw{P}_3\right)$

由微分方程稳定性定理可知，当培训机构选择“积极转型”策略的概率z满足： $H\left(z\right)=0$ 且 $\frac{\text{d}H\left(z\right)}{\text{d}z}<0$ 时，z为培训机构策略选择的演化稳定点。因此，当 $0<w<w_1$ 时，由 ${H\left(z\right)|}_{z=0}=0$ ， ${\frac{\text{d}H\left(z\right)}{\text{d}z}|}_{z=0}<0$ ，可知 $z=0$ 为演化稳定点，表明当家庭选择“不参加校外学科培训”策略低w₁时，培训机构最终选择“转为地下”策略。当 $w_1<w<1$ 时，由 ${H\left(z\right)|}_{z=1}=0$ ， ${\frac{\text{d}H\left(z\right)}{\text{d}z}|}_{z=1}<0$ ，可知 $z=1$ 为演化稳定点，表明当家庭选择“不参加校外学科培训”策略高于w₁时，培训机构最终选择“积极转型”策略。

命题3当培训机构积极转型的成本、家庭参加学科培训的收益等增加时，机构“转向地下”的概率会增加。

证明：培训机构策略选择的相位图如图4。图中的空间被曲面 $w=w_0$ 划分位I和II两个部分，其体积记为 ${\text{V}}_{z_1}$ 和 ${\text{V}}_{z_0}$ ，分别表示培训机构选择“积极转型”策略的概率和“转为地下”策略的概率。空间I是满足 $w_1<w<1$ 的初始策略集，由引理3可知，当培训机构初始状态位于空间I时，机构最终会选择“积极转型”策略。下面的空间II是满足 $0<w<w_1$ 的初始策略集，由引理3可知，当学校初始状态位于空间II时，政府最终会选择“转向地下”策略。于此同时，在其他变量不变的条件下，随着C₄，S₂增大，w₁将会增大，导致空间II增大，此培训时机构选择“转向地下”的概率增大。另一方面，C₅，w₁，R₃增大，w₁将会减小，导致空间I增大，此时培训机构选择“积极转型”的概率增大。

Figure 4. The phase diagram of training institution policy choices

图4. 培训机构策略选择的相位图

4.4. 家庭策略选择的稳定性分析

家庭选择“不参加学科培训”策略和“积极参加学科培训”策略的期望收益分别为：

$E_{41}=y{P}_6-P_6+x{R}_2+y{R}_4+z{R}_7-z{S}_3$

$E_{42}=R_8-S_2+x{R}_2+y{R}_4-z{R}_8+z{S}_2+\gamma z{R}_7$

因此，家庭的期望收益为：

$\overline{E_4}=w{E}_{41}+\left(1-w\right)E_{42}$

相应地，培训机构的复制动态方程为：

$C\left(w\right)=w\left(E_{41}-\overline{E_4}\right)=w\left(w-1\right)\left(P_6+R_8-S_2-y{P}_6-z{R}_7-z{R}_8+z{S}_2+z{S}_3+z\gamma R_7\right)$

接下来，我们讨论机构“积极转型”概率z的变化对家庭策略选择的影响。令 $z_0=-\frac{P_6+R_8-S_2-y{P}_6}{S_2-R_8-R_7+S_3+\gamma R_7}$

可知：

1) 当 $z=z_0$ 时， $C\left(w\right)\equiv 0$ ，因此任意 $w\in \left[0,1\right]$ 均为稳定点；

2) 当 $z\ne z_0$ 时，由 $C\left(w\right)=0$ ，可以推出 $w=1$ 或 $w=0$ ，即家庭“不参加校外学科培训”和“积极参加校外学科培训”都是稳定策略。

引理4：1) 当 $S_2-R_8-R_7+S_3+\gamma R_7>0$ 时， $0<z<z_0$ 时， $w=1$ 为家庭演化稳定点， $z_0<z<1$ 时， $w=0$ 为演化稳定点；

2) 当 $S_2-R_8-R_7+S_3+\gamma R_7<0$ 时， $0<z<z_0$ 时， $w=0$ 为家庭演化稳定点， $z_0<z<1$ 时， $w=1$ 为演化稳定点；

证明：对 $C\left(w\right)$ 关于变量w求一阶偏导，可得

$\frac{\text{d}C\left(w\right)}{\text{d}w}=\left(2w-1\right)\left(P_6+R_8-S_2-y{P}_6-z{R}_7-z{R}_8+z{S}_2+z{S}_3+z\gamma R_7\right)$

1) 当 $S_2-R_8-R_7+S_3+\gamma R_7>0$ 时，即R₈相对较小，也就是家庭参加校外学科培训时的增益不大时。

由微分方程稳定性定理可知，当家庭选择“不参加校外学科培训”策略的概率w满足： $C\left(w\right)=0$ 且 $\frac{\text{d}C\left(w\right)}{\text{d}w}<0$ 时，w为家庭策略选择的演化稳定点。因此，当 $0<z<z_0$ 时，由 ${C\left(w\right)|}_{w=1}=0$ ， ${\frac{\text{d}C\left(w\right)}{\text{d}w}|}_{w=1}<0$ ，可知 $w=1$ 为演化稳定点，表明当培训机构选择“积极转型”策略低z₀时，家庭最终选择“不参加校外学科培训”策略。当 $z_0<z<1$ 时，由 ${C\left(w\right)|}_{w=0}=0$ ， ${\frac{\text{d}C\left(w\right)}{\text{d}w}|}_{w=0}<0$ ，可知 $w=0$ 为演化稳定点，表明当培训机构选择“积极转型”策略高于z₀时，家庭最终选择“积极参加校外学科培训”策略。

2) 当 $S_2-R_8-R_7+S_3+\gamma R_7<0$ 时，即R₈相对教大，也就是家庭参加校外学科培训时的收益较大时。

由微分方程稳定性定理可知，当家庭选择“不参加校外学科培训”策略的概率w满足： $C\left(w\right)=0$ 且 $\frac{\text{d}C\left(w\right)}{\text{d}w}<0$ 时，w为家庭策略选择的演化稳定点。因此，当 $0<z<z_0$ 时，由 ${C\left(w\right)|}_{w=0}=0$ ， ${\frac{\text{d}C\left(w\right)}{\text{d}w}|}_{w=0}<0$ ，可知 $w=0$ 为演化稳定点，表明当培训机构选择“积极转型”策略低z₀时，家庭最终选择“积极参加校外学科培训”策略。当 $z_0<z<1$ 时，由 ${C\left(w\right)|}_{w=1}=0$ ， ${\frac{\text{d}C\left(w\right)}{\text{d}w}|}_{w=1}<0$ ，可知 $w=1$ 为演化稳定点，表明当培训机构选择“积极转型”策略高于z₀时，家庭最终选择“不参加校外学科培训”策略。

命题4家庭因不参加学科培训的焦虑增加时，家庭“积极参加校外学科培训”的概率增加。

证明：家庭策略选择的相位图如图5。两图中的空间被曲面 $z=z_0$ 划分位I和II两个部分，选择其体积记为 ${\text{V}}_{w_1}$ 和 ${\text{V}}_{w_0}$ ，分别表示家庭选择“不参加校外学科培训”策略的概率和“积极参加校外学科培训”策略的概率。

当 $S_2-R_8-R_7+S_3+\gamma R_7>0$ 时，左图空间II是满足 $z_0<z<1$ 的初始策略集，由引理4(1)可知，当家庭初始状态位于空间II时，家庭最终会选择“积极参加校外学科培训”策略。同时在其他变量不变的条件下，随着P₆增大，z₀将会减小，导致空间II增大，此时家庭选择“积极参加校外学科”的概率增大。由此说明，当家庭不参加学科培训的焦虑增加时，家庭“积极参加校外学科”的意愿会有所增加。

当 $S_2-R_8-R_7+S_3+\gamma R_7<0$ 时，由引理4(2)可知，当家庭初始状态位于空间I时，家庭最终会选择“不参加校外学科培训”策略。同时在其他变量不变的条件下，随着P₆增大，z₀将会增大，导致空间II增大，此时家庭选择“积极参加校外学科”的概率增大。由此说明，当家庭不参加学科培训的焦虑增加时，家庭“积极参加校外学科培训”的意愿会有所增加。

综上，不论是哪种情况，家庭不参加学科培训的焦虑增加，都会增加家庭“积极参加校外学科培训”的概率。

Figure 5. The phase diagram of family policy choices

图5. 家庭策略选择的相位图

5. 策略组合的稳定性分

本节，我们将在之前分析的各方演化稳定策略及部分因素对策略选择影响的基础上，进一步讨论四方主体共同作用下的演化稳定策略。

根据各方的复制动态方程，构建减负政策四方复制动态系统：

$\{\begin{array}{l}F\left(x\right)=x\left(x-1\right)\left(C_1-P_1-P_4-R_1+S_1-\beta C_1+y{P}_4+z{P}_1\right)\hfill \\ G\left(y\right)=-y\left(y-1\right)\left(w{P}_5-C_3+x{P}_2\right)\hfill \\ H\left(z\right)=-z\left(z-1\right)\left(\alpha C_5-S_2-C_4+x{C}_5+x{P}_1-y{P}_3+w{S}_2+w{S}_3+y{R}_3-\alpha x{C}_5+2yw{P}_3\right)\hfill \\ C\left(w\right)=w\left(w-1\right)\left(P_6+R_8-S_2-y{P}_6-z{R}_7-z{R}_8+z{S}_2+z{S}_3+z\gamma R_7\right)\hfill \end{array}$

引理6复制动态系统拥有16组均衡策略组。

证明：四方博弈主体策略组合的稳定性判断可以参照Lyapunov的第一法则。令 $F\left(x\right)=0$ ， $G\left(y\right)=0$ ， $H\left(z\right)=0$ ， $C\left(w\right)=0$ 同时成立，由Ritzberger和Selten可知，在有多个种群的演化博弈中，演化博弈的稳定解为严格纳什均衡，即纯策略。因此，在当地政府、学校、培训机构、家庭的复制动态系统中，符合条件的均衡策略组合共有16组。

接下来，讨论当地政府、学校、培训机构、家庭四方演化博弈中16组均衡策略组的稳定性。为此，我们将构建四方复制动态系统的雅可比矩阵：

$J=\left(\begin{array}{llll}\frac{\partial F\left(x\right)}{\partial x}\hfill & \frac{\partial F\left(x\right)}{\partial y}\hfill & \frac{\partial F\left(x\right)}{\partial z}\hfill & \frac{\partial F\left(x\right)}{\partial w}\hfill \\ \frac{\partial G\left(y\right)}{\partial x}\hfill & \frac{\partial G\left(y\right)}{\partial y}\hfill & \frac{\partial G\left(y\right)}{\partial z}\hfill & \frac{\partial G\left(y\right)}{\partial w}\hfill \\ \frac{\partial H\left(z\right)}{\partial x}\hfill & \frac{\partial H\left(z\right)}{\partial y}\hfill & \frac{\partial H\left(z\right)}{\partial z}\hfill & \frac{\partial H\left(z\right)}{\partial w}\hfill \\ \frac{\partial C\left(w\right)}{\partial x}\hfill & \frac{\partial C\left(w\right)}{\partial y}\hfill & \frac{\partial C\left(w\right)}{\partial z}\hfill & \frac{\partial C\left(w\right)}{\partial w}\hfill \end{array}\right)$

Table 3. Analysis of the asymptotic stability of equilibrium points in replicator dynamic systems under strict local government regulation

表3. 地方政府严格监管下复制动态系统均衡点渐进稳定分析

注：U表示该特征值的正负无法判断

Table 4. Analysis of the asymptotic stability of equilibrium points in replicator dynamic systems under passive local government regulation

表4. 地方政府消极监管下复制动态系统均衡点渐进稳定分析

注：U表示该特征值的正负无法判断

根据Lyapunov第一法则，演化稳定策略组合对应的雅克比矩阵特征值应均小于0。为此，我们计算各均衡点对应的雅克比矩阵特征值，如表所示，其中上表为家庭选择“积极参加校外学科培训”策略时，各稳定点的雅克比矩阵特征值；下表为家庭选择“不参加校外学科培训”策略时，各个稳定点的雅克比矩阵特征值。

从表3和表4来看，只有两个均衡点 $\left(0,1,0,0\right)$ 和 $\left(0,1,1,0\right)$ 确定是不稳定点，而对于其他均衡点，其是否为ESS与演化博弈中的各个参数赋值有关。由于本次“双减”的最终目的，是希望达到学校“积极提升质量”、培训机构“积极转型”、家庭“不参加学科培训”，所以我们把分析的焦点放在最后的两个均衡点 $\left(0,1,1,1\right)$ 和 $\left(1,1,1,1\right)$ 。

首先，我们可以看到，这两个均衡点对应的特征值有一个是相同的，即 $S_3-R_7+\gamma R_7$ ，为了这两个均衡点最后博弈的ESS，参数必须满足 $S_3-R_7+\gamma R_7<0$ ，即R₇要相对S₃要足够大。

第二，我们可以看到，这两个均衡点对应的特征值有一个互为相反，也就是这两个均衡点不能同时是博弈的ESS。

当 $C_1-R_1+S_1-\beta C_1<0$ ，即 $\left(1-\beta \right)C_1+S_1<R_1$ 时，均衡点 $\left(1,1,1,1\right)$ 是我们追求的目标。若此时还能满足 $C_3-P_2-P_5<0$ ，博弈大概率会收敛到均衡点 $\left(1,1,1,1\right)$ ，因为 $C_4-C_5-P_1-P_3-R_3-S_3<0$ 较为容易实现。

当 $C_1-R_1+S_1-\beta C_1>0$ ，即 $\left(1-\beta \right)C_1+S_1>R_1$ 时候，均衡点是 $\left(0,1,1,1\right)$ 我们追求的目标。若此时还能满足 $C_3-P_5<0$ 时，基本上博弈会收敛到均衡点 $\left(0,1,1,1\right)$ ，因为 $C_4-C_5-P_1-P_3-R_3-S_3<0$ 较为容易实现。

6. 仿真分析

在本节中，我们通过MATLAB 2017进行数值仿真，验证演化稳定性分析的有效性，用更为直观的方式研究复制动态系统中关键要素对多方博弈演化过程及演化结果的影响。根据对实际情况的估计，演化博弈中的各参数赋值由第4节中的稳定性分析可知，由于策略组合 $\left(0,1,1,1\right)$ 和 $\left(1,1,1,1\right)$ 是本此“双减”政策的长期目标。

首先我们对R₁取不同值时的收敛情况来看(其他参数设置均为 $R_2=30$ ， $R_3=15$ ， $R_4=20$ ， $R_5=10$ ， $R_6=20$ ， $R_7=80$ ， $R_8=30$ ， $C_1=50$ ， $C_2=50$ ， $C_3=20$ ， $C_4=20$ ， $C_5=20$ ， $S_1=30$ ， $S_2=150$ ， $S_3=30$ ， $P_1=50$ ， $P_2=10$ ， $P_3=30$ ， $P_4=20$ ， $P_5=25$ ， $P_6=20$ ， $P_7=50$ ， $\alpha =0.2$ ， $\beta =0.2$ ， $\gamma =0.5$ )

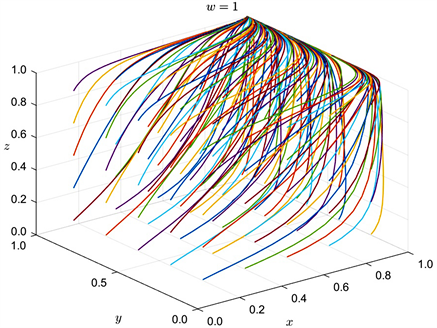
Figure 6. Evolution process of each party’s strategy when $R_1=100$

图6. $R_1=100$ 时各方策略演化过程

Figure 7. Evolution process of each party’s strategy when $R_1=10$

图7. $R_1=10$ 时各方策略演化过程

可以从图6和图7看出政府在不同的严管收益下，皆有可能实现“双减”政策的长期目标。

从图8可以看到，随着转型机构对家庭的积极影响逐渐增大时，家庭中选择“不参加学科培训”的概率会稳定于1。因此，引导转型机构的发展并教育家庭价值观变得至关重要。

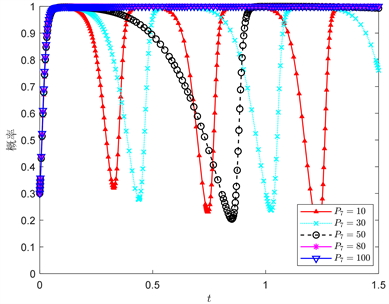
Figure 8. Impact of the magnitude of positive influence from proactive transformation institutions on family choices

图8. 积极转型机构对家庭的积极影响大小对家庭选择的影响

从图9可以看出若是地方政府严格监管时对自身的收益不够时，地方政府会趋于“消极监管”。由此可以看到，“双减”政策的长效落实，需要一直保持政策强度，使之在地方政府的行政目标中一直占有重要地位。

Figure 9. Impact of profits during strict government regulation on self-selection

图9. 政府严格监管时的收益对自身选择的影响

从图10可以看出，随着学校在不提升质量时受到的负面评价愈大，学校选择提升其自身教育教学质量的概率越大。这说明，在“双减”政策实施中，保持社会对学校评价渠道的畅通至关重要。同时，把学校评价纳入到行政教育部门对学校的评估中的举措也值得探索。

Figure 10. Impact of the magnitude of negative influence from families not participating in subject training on the decision-making of schools not improving quality

图10. 学校不提升质量时受到不参加学科培训家庭的负面影响大小对其决策的影响

7. 总结与建议

本研究通过分析教育生态四方主体的博弈，针对实现学校“积极提升质量”、机构“积极转型”、家庭“不参加学科培训”的长期目标，得出以下主要结论：

1) 保持政策强度降低地方政府监管负担对于实现“双减”政策的长期目标非常关键。

2) 转型后的机构对家庭的吸引力要足够大，对家庭的积极影响要足够大。这可以通过督导机构、教育家庭和社会引导三个方向来实现。

3) 在政策执行过程中，政府要采取一系列措施来推动学校提升质量，并减少学校提升质量的成本 [19] [20] 。

在结束本文之际，必须再次强调，义务教育阶段的学业负担问题根源于深层次的社会问题。过重的学业负担不是一朝一夕形成的，因此治理这一问题也不能期待一蹴而就。“双减”政策的长期执行，既要牢记建设高质量教育体系和构建优质教育生态的重要任务，同时也需要持续关注并解决在实施过程中出现的新问题。