1. 引言
近年来,机器视觉技术快速发展,在三维领域的机器视觉技术包括三维重建、SLAM (simultaneous ocalization and mapping)、目标识别等技术被广泛研究,使得三维机器视觉技术在逆向工程、无人驾驶、增强现实等领域受到广泛应用 [1] 。在点云三维重建过程中,由于受到采集条件的限制,3D相机在一次采集中只能获得采集目标一个视角的点云数据,所以采集过程需要重复多次,得到采集目标多个视角下的点云数据,将这些不同视角的点云数据变换到统一坐标系下的操作被称为点云配准。
点云配准是将不同视角下的点云数据转换到同一坐标系下的技术,目前使用最广泛的配准技术是粗配准后精配准的配准策略。常用于粗配准的算法如正态分布变换(Normal Distributions Transform, NDT)算法 [2] 和采样一致性初始配准(Sample Consensus Initial Aligment, SAC-IA)算法 [3] ,用于精配准的常用算法如迭代最近点(Iterative Closest Point, ICP)算法 [4] 及其各种变式算法 [5] [6] [7] 。王文博等人 [8] 提出了改进的ICP点云配准方法,使用点云分块并从分块点云中提取尺度不变特征变换(Scale Invariant Feature Transform, SIFT)特征点的思想,将特征点用于SAC-IA + ICP的配准策略,大幅提升了配准的效率和精度,但点云分开的阈值选择较为麻烦。刘雷等人 [9] 提出了基于SIFT结合二进制直方图描述子的点云配准方法,可以有效提升重叠率较低的两个点云配准的效率和精度,但在一般情况下配准精度仍有提升的空间。范林林等人 [10] 提出一种基于区域均值特征描述符的部分点云与整体点云配准方法,与现有的基于局部特征描述符的点云配准方法相比,有效提高了配准的速度和准确度,但点云的密度对其特征描述造成的影响较大,存在局限性。张赵良等人 [11] 提出用内部描述子(Intrinsic Shape Signature, ISS)特征点结合改进ICP的配准算法,将配准精度和配准效率进一步提高,但该算法的参数设置较为复杂,通用性较差。
针对以上配准算法存在的问题,本文提出基于SIFT关键点提取结合改进ICP的点云配准算法,采用SIFT计算点云特征点,在保证配准精度的条件下减少点云配准过程的计算量,对提取的特征点计算其快速点特征直方图(Fast Point Feature Histograms, FPFH)局部描述子,得到对应点对,再利用SAC-IA算法完成粗配准,最后使用带法向向量约束的点到平面的ICP算法完成精配准。
2. 算法原理
2.1. SCI-IA粗配准
SAC-IA算法基于随机采样一致性(Random sample consensus, RANSAC)算法,不同之处在于RANSAC算法是随机采样点,而SAC-IA算法的采样点数量更多,采样点之间的关系有距离限制,在对应点查找时,通过FPFH来匹配而不是点与点之间的距离,特征描述符考虑了点的领域结构,增加了寻找匹配点的精度。SAC-IA的算法步骤如下:
(1) 分别计算源点云和目标点云的FPFH特征描述子;
(2) 寻找两组点云中有相似FPFH的匹配点;
(3) 随机选择n对(n > 3)匹配点;
(4) 通过SVD求解该匹配情况下的旋转位移矩阵,并计算配准误差;
(6) 重复步骤(3)~(5),直到满足误差条件,输出最终的旋转位移矩阵。
2.2. ICP精配准
ICP算法本质上是基于最小二乘法的思想,配准精度高,不需要提供特征点,但对于点云的初始位姿敏感,需要在ICP算法之前进行点云粗配准,否则容易陷入局部最优,其核心是通过一定的约束关系找到源点云和目标点云之间的对应点,利用对应点构建目标函数并进行迭代优化,直至目标函数收敛或达到最大迭代次数。
设源点云为P,目标点云为Q,ICP算法可描述为:
(1)
其中,R为点云旋转变换矩阵;T为点云平移向量;np、nq分别为源点云和目标点云中点的数量。pi、qi分别为源点云和目标点云中的一点;
ICP算法步骤如下:
(1) 计算源点云P中的每一个点pi与目标点云Q中的对应点qi。
(2) 通过欧式距离去除错误匹配点对。
(3) 通过SVD分解计算使得对上述对应点对平均距离最小的刚体变换,求得旋转平移矩阵R和T;
(4) 使用旋转平移矩阵对P进行空间变换,得到新的点云P':
(2)
(5) 计算P'与Q的距离误差,若满足收敛条件或达到最大迭代次数,则停止迭代,否则将点集P'作为新的P继续迭代计算旋转平移矩阵,直到满足目标函数要求。
3. 改进算法原理

Figure 1. The overall flow chart of the algorithm in this paper
图1. 本文算法总体流程图
为了提高ICP算法配准的效率,减少迭代次数,本文使用SAC-IA进行粗配准,为ICP算法提供较好的初始位姿,并在粗配准之前,使用SIFT算法提取源、目标点云的关键点,在保留点云特征的同时减少配准计算量。另外,使用点到面的距离误差作为ICP算法的目标函数,并且添加法向量夹角阈值来剔除配准时引入的噪声点对,提高配准精度。本文算法的总体流程如图1所示。
3.1. SIFT特征点提取
SIFT算法是David G.Lowe在1999年提出的高效区域检测算法,在2004年得以完善,在2007年由Flint等人应用于3D数据上 [12] ,该方法提取的特征点具有对噪声、旋转和平移等因素保持较好的不变性的特点。其主要原理是在目标点集的不同尺度空间上搜索那些对于尺度和旋转不变的特征点。对于有N个点的点云数据P,任意一点pi的坐标为(xi, yi, zi),i = 1, 2, …, N,SIFT特征点提取算法步骤如下:
(1) 构建尺度空间:将点云与三维高斯函数进行卷积,计算尺度空间L (x, y, z, s)。
(3)
其中,G (x, y, z, ks)为高斯卷积核函数,p (x, y, z)为点云坐标,s为空间尺度参数,k为尺度空间大小调整参数。三维空间中的高斯卷积核函数如下:
(4)
(2) 计算高斯差分模型:设s为高斯金字塔每组的层数,将高斯金字塔中相邻的两层点云相减,构成点云的高斯差分图DoG,如式:
(5)
其中,DoGi为相邻尺度层的差分模型,i∈(0, s + 2)。
(3) 特征点检测:计算DOGi在本层内的极值点,并与其上下2个尺度层内的极值点对比仍为最值时,则认为该点为特征点。
3.2. 带法向约束的点到面ICP算法
如式(1)所示,普通ICP算法的以点到点之间的距离误差作为目标函数进行迭代求解,而点到平面的ICP算法以最小化源点云中的点到目标点云对应点所在平面的距离作为配准准则,如式(6):
(6)
其中,ni为qi处的单位法向量。
如图2所示为点到点(point to point) ICP与点到平面(point to plane) ICP的示意图,P和Q分别代表源点云和目标点云。相较于点到点的ICP算法,点到平面的ICP算法更能体现点云的空间结构,能更好地抵抗错误对应点对,迭代收敛的速度更快。
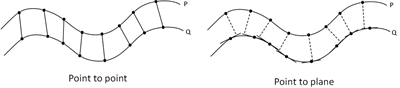
Figure 2. Schematic diagram of distance calculation
图2. ICP距离计算示意图
在ICP获取匹配点云对时,容易引入噪声,使得特征点不能完全的一一对应,对配准结果产生影响。对此,参考文献 [13] 的方法,通过设置法向量约束条件来剔除误匹配点。具体方法为:对于特征点对A和B,其法向量分别为nA和nB,当nA和nB差距越大,其夹角的余弦值越小,通过设置夹角余弦阈值F,将法向量nA和nB的夹角余弦值小于F的点视为误匹配点,并将其剔除。
4. 实验结果与分析
本文使用斯坦福大学提供的标准点云扫描数据bunny、Armadillo和happy作为实验对象,将同一点云模型在两个不同视角下的数据作为配准实验的源点云与目标点云,以本文算法作为实验组,SAC_IA + ICP算法和NDT + ICP算法作为对照组进行实验,通过比较三种算法的配准结果和性能指标,来验证本文算法的可行性。
4.1. 实验结果
如图3中(a)所示为3个待配准点云对象的源点云和目标点云,将这3个点云模型经过本文算法、SAC-IA + ICP算法和NDT + ICP算法后,得到其后(b)、(c)、(d)所示的配准结果。
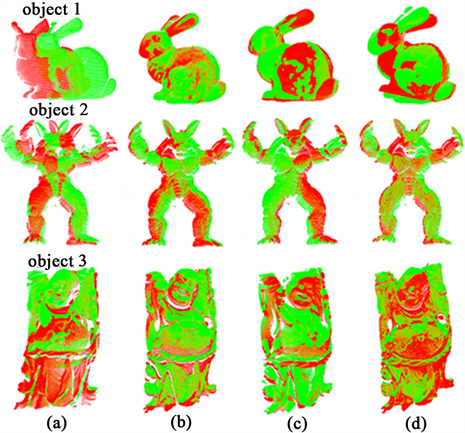
Figure 3. The experimental results of the three groups. (a) Point cloud to be registered; (b) Proposed algorithm. (c) SAC-IA + ICP algorithm; (d) NDT + ICP algorithm
图3. 三组实验结果(a) 待配准点云;(b) 本文算法;(c) SAC-IA + ICP算法(d) NDT + ICP算法
通过图3可以直观地看出,在三组实验中,本文算法的配准结果均比其余两个算法的配准效果好,配准后的源点云和目标点云能更加贴合在一起,说明本文算法在配准精度上更优于传统的SAC-IA + ICP算法和NDT + ICP算法。
4.2. 算法性能分析
为了更直观地分析本文算法的性能,通过统计3个算法的耗时与配准结果的均方根误差(MSE),如表1~3所示,来比较3个算法的性能。为保证算法的可比性,在保证配准精度变化不大的情况下,使用体素网络下采样的方法对SAC-IA + ICP算法和NDT + IC算法的数据进行下采样操作,得到下采样后的精简点,再使用此精简点集执行后续配准操作。

Table 1. Algorithm performance in this paper
表1. 本文算法性能

Table 2. Algorithm performance of SAC-IA + ICP
表2. SAC-IA + ICP算法性能

Table 3. Algorithm performance of NDT + ICP
表3. NDT + ICP算法性能
从表1~表3可以看出,本文算法使用了SIFT关键点提取算法后,可以将原始点集的数量大幅缩减,减少到原来点数的1.5%左右,而SAC-IA + ICP算法和NDT + ICP算法由于使用的是传统的下采样来精简点云数量,在保证精度的条件下精简后的点云数量为原来的40%左右,使得用于粗配准和精配准的点云数目较多,所以算法更加耗时。另外,从配准的MSE上可以看出,本文算法相比于另外两种算法拥有更加小的MSE,说明本文算法配准结果更加精细。通过统计平均数据可知,本文算法在算法耗时上相比于SAC-IA + ICP算法提高了96.2%、相比于NDT + ICP算法提高了81.0%,在MSE上相比于SAC-IA + ICP算法提高了43.6%、相比于NDT + ICP算法提高了24.7%。
5. 总结
本文针对传统配准方法中的粗配准后精配准的策略耗时长、精度低的问题,提出使用SIFT提取原始点云的特征点,在保留原始点云关键特征的条件下尽可能低降低了配准过程的数据量,再将这些特征点经过SAC-IA粗配准后,通过结合了法向约束的点到面ICP算法进行精配准,大大提高了配准的效率,相较于传统配准策略在算法耗时和配准精度上均有明显的提升,证明了本文算法的有效性。
NOTES
*通讯作者。