非Kolmogorov湍流中激光光斑漂移的统计模拟

Statistical Simulation of Laser Spot Drift in Non-Kolmogorov Turbulence

摘要: 激光光束在湍流大气传输过程中光斑位置发生漂移，从而影响目标跟踪、激光通信等应用。本文采用功率谱反演法和低频补偿法构建等效结构常数的非Kolmogorov湍流随机相位屏，模拟高斯光束在非Kolmogorov湍流传输过程，对产生的光斑漂移量进行研究，提出了基于贝叶斯定理的光斑漂移估计模型。实验结果表明：漂移量估计精度随湍流强度和传输距离的增大而减小。光斑后验模型相较于移动平均模型的平均绝对误差小，估计精度较高。

Abstract: The spot position of the laser beam drifts during turbulent atmospheric transmission, which affects the application of target tracking and laser communication. In this paper, the power spectrum in-version method and the low-frequency compensation method are used to construct a non-Kolmogorov turbulent stochastic phase screen with equivalent structural constants, which simulates the turbulent transmission process of Gaussian beams in non-Kolmogorov flows, and the resulting spot drift is studied, and a spot drift estimation model based on Bayes’ theorem is pro-posed. The experimental results show that the accuracy of drift estimation decreases with the in-crease of turbulence intensity and propagation distance. Compared with the moving average model, the average absolute error of the spot posterior model is smaller, and the estimation accuracy is higher.

1. 引言

激光在大气中传输时，折射率的随机起伏，使得光束波前发生畸变，在通过光学系统时发生位置偏移现象，产生光斑漂移这一大气湍流效应 [1] [2] [3] 。在目标跟踪中，光斑漂移可能导致目标位置的偏移，影响目标的定位和跟踪精度。因此研究大气湍流对光斑漂移的影响，对激光大气传输的应用具有重要意义。

湍流是一种高度复杂的现象，研究人员通常在Kolmogorov湍流，即在均匀各向同性的假设下，研究光束在传输过程中产生的光斑漂移。王晓章等 [4] 采用多层相位屏法和分步傅里叶算法相结合的方式模拟环形艾里光束在湍流大气中传输时光斑质心漂移，实验结果表明，湍流强度与相位屏数量都影响漂移量大小。朱东济等 [5] 基于贝叶斯定理对随机模拟产生的基模激光漂移进行分析，实验表明不同的漂移测量值和真实值误差对漂移估计值的影响较大。Wang等 [6] 基于时间序列分析理论，建立漂移的ARMA模型，模型的数学期望值作为滤波结果，滤波后可以获得较高的漂移预测精度且长距离传输对漂移预测精度影响较大。姜楠 [7] 等分析大气湍流对不同波长激光传输特性的影响，研究发现波长不影响光斑漂移大小，随着湍流强度的增强，漂移方差越来越大。

然而实际大气偏离了Kolmogorov湍流特征，主要表现为：功率谱幂律偏离Kolmogorov湍流幂律，即不严格符合-11/3定律 [8] 。为了反映真实大气中光斑漂移对空间光通信的影响，研究人员对激光光束在非Kolmogorov湍流传输产生的光斑漂移进行研究。Cheng等 [9] 分析了各向异性湍流中Bessel-Gaussian光束的光斑漂移，发现各向异性对漂移产生一定的影响，并且漂移量随拓扑电荷的增加而减小。狄颢萍等 [10] 采用功率谱反演法与非均匀采样相结合的方法，引入与湍流尺度相关的各向异性因子，生成相位屏，研究圆艾里高斯涡旋光束经过各向异性非Kolmogorov湍流大气后的漂移特性，研究发现漂移量随湍流外尺度增大而增大，且各向异性系数越小漂移量越大，漂移量随着幂律、大气相干长度、传输距离的增大而增大。Cui等 [11] 研究了各向异性湍流对高斯光束光斑漂移的影响，结合有效各向异性因子、湍流内外尺度、幂律对光斑漂移进行分析，验证各向异性因子对光斑漂移的影响。

上述研究人员对引起光斑漂移的物理和环境因素进行分析，旨在讨论大气湍流和光束参数对光斑漂移的影响。传统的Kolmogorov理论基于固定的幂律，限制了模拟精度的进一步提高，为了更全面地了解大气湍流，需要采用幂律的随机分布进行模拟。数值模拟的核心是生成合适的相位屏从而代替光传播路径上湍流引起的光波的相位起伏。为了提高目标定位的准确性，需要讨论非Kolmogorov湍流对光斑漂移的影响，考虑湍流强度、传输距离、相位屏数量等影响漂移量大小的因素并对光斑漂移量进行估计。

本文给出了高斯光束在非Kolmogorov湍流中传输产生的光斑漂移的统计模拟，分析湍流强度和幂律对漂移的影响，并研究传输距离和相位屏数量对漂移估计精度的影响。

2. 研究方法

为了实现高斯光束在非Kolmogorov湍流中的统计模拟，本文基于功率谱反演法和低频补偿法构造非Kolmogorov湍流相位屏，并用幂律模拟传播路径的湍流非均匀性。数值模拟高斯光束在非Kolmogorov湍流传输，对产生的光斑漂移二维图像进行质心定位，得到光斑漂移量，根据贝叶斯定理对光斑漂移进行后验估计。

2.1. 非Kolmogorov湍流相位屏

常用的相位屏方法包含谱反演法和Zernike多项式法，由于谱反演法生成的相位屏具有低频不足的缺点，Zernike多项式法生成的相位屏具有高频不足的缺点，两种方法都无法全面描述湍流信息。因此本文采用谱反演法和低频补偿法相结合，模拟具有更全面湍流信息的相位屏。

相位屏的思想是把连续的随机介质分割成一系列厚度为Δz的平行薄屏，屏前表面的光场E₀经过相位调制在屏的后表面形成光场E₁ [12] 。光束依次通过每个薄屏，这样就可以将连续的随机介质看作是在真空中放入一系列无限薄的相位屏。光束传输过程如图1所示。

Figure 1. Beam transmission process

图1. 光束传输过程

Kolmogorov湍流下功率谱反演法 [12] [13] 的基本思想是，首先生成复高斯随机数矩阵 $h\left({\kappa }_x,{\kappa }_y\right)$ ，接着对其用符合大气湍流的功率谱密度函数 $F_{\Phi }\left({\kappa }_x,{\kappa }_y\right)$ 进行滤波，最后进行逆傅里叶变换得到大气湍流相位屏：

$\phi \left(x,y\right)={\displaystyle \underset{{\kappa }_x}{\sum }{\displaystyle \underset{{\kappa }_y}{\sum }h\left({\kappa }_x,{\kappa }_y\right)}}\sqrt{F_{\Phi }\left({\kappa }_x,{\kappa }_y\right)}\exp \left(j\left({\kappa }_{x}x+{\kappa }_{y}y\right)\right)\Delta {\kappa }_x\Delta {\kappa }_y$ (1)

式中空域内 $x=m\Delta x$ ， $y=n\Delta y$ ， $\Delta x,\Delta y$ 为x、y方向上的采样间隔，波数域内 ${\kappa }_x=m^{\prime }\Delta {\kappa }_x,{\kappa }_y=n^{\prime }\Delta {\kappa }_y$ 为湍流随机相位屏x、y方向上的采样间隔，采样频率为 $\Delta {\kappa }_x,\Delta y$ ， $m,n,m^{\prime },n^{\prime }$ 为整数。

要产生非Kolmogorov湍流相位屏，需要非Kolmogorov湍流等效结构常数和功率谱函数。折射率结构常数是描述湍流特性的重要参数，采用李玉杰等人 [14] 根据理论推导得到的非Kolmogorov湍流等效结构常数：

${\tilde{C}}_n^2\left(\alpha ,z\right)=L_0^{11/3-\alpha }{C}_n^2\left(z\right)$ (2)

式中 $C_n^2\left(z\right)$ 为Kolmogorov湍流折射率结构常数， $\alpha$ 为功率谱幂律， $L_0$ 大气湍流外尺度。非Kolmogorov湍流功率谱函数 [8] 为：

${\tilde{F}}_{\Phi }\left(\kappa \right)=A\left(\alpha \right){\tilde{C}}_n^2\left(\alpha ,z\right){\kappa }^{-\alpha }$ (3)

式中 $A\left(\alpha \right)=2^{\alpha -6}\left({\alpha }^2-5\alpha +6\right){\pi }^{-\frac{3}{2}}\frac{\Gamma \left[\frac{\alpha }{2}-1\right]}{\Gamma \left[\frac{5-\alpha }{2}\right]},3<\alpha <5$ 为广义振幅， $\kappa$ 为空间波数。

将(3)式代入(1)式进行二维傅里叶逆变换并离散化，得到非Kolmogorov湍流相位屏：

$\begin{array}{l}\tilde{\phi }\left(x,y\right)={\displaystyle \underset{-\frac{N_x}{2}}{\overset{\frac{N_x}{2}-1}{\sum }}{\displaystyle \underset{-\frac{N_y}{2}}{\overset{\frac{N_y}{2}-1}{\sum }}h\left(m^{\prime },n^{\prime }\right)\tilde{f}\left(m^{\prime },n^{\prime }\right)\exp \left(j2\pi \left(\frac{m^{\prime }m}{N_x}+\frac{n^{\prime }n}{N_y}\right)\right)}}\\ \tilde{f}\left(m^{\prime },n^{\prime }\right)=\sqrt{\frac{A\left(\alpha \right)}{0.033}{\left(f_x^2+f_y^2\right)}^{\frac{\frac{11}{3}-\alpha }{2}}{L}_0^{\frac{11}{3}-\alpha }}\frac{2\pi }{\sqrt{G_x{G}_y}}\sqrt{0.00058}{r}_0^{-\frac{5}{6}}{\left(f_x^2+f_y^2\right)}^{-\frac{11}{12}}\end{array}$ (4)

式中 $r_0=0.185{\left(\frac{1}{{\lambda }^2}{\displaystyle {\int }_0^L{C}_n^2\left(\alpha ,z\right)\text{d}z}\right)}^{-3/5}$ 为大气相干度， $f=\frac{\kappa }{2\pi }$ ， $G_x,G_y$ 分别为x、y方向上的抽样点数； $N_x,N_y$ 为网格数。

低频补偿的基本思想 [15] [16] 是在对傅里叶低频次谐波重采样的基础上进行插值合并，从而对相位屏进行次谐波低频补偿。采用Lane等 [16] 提出的生成次谐波的方法：

${\phi }_{SH}\left(j\Delta x,j\Delta y\right)={\displaystyle \underset{p=1}{\overset{N_p}{\sum }}{\displaystyle \underset{m=-1}{\overset{1}{\sum }}{\displaystyle \underset{n=-1}{\overset{1}{\sum }}h\left(m^{\prime },n^{\prime }\right)\tilde{f}\left(m^{\prime },n^{\prime }\right)\exp \left(j2\pi \left(\frac{m^{\prime }m}{3^p{N}_x}+\frac{n^{\prime }n}{3^p{N}_y}\right)\right)}}}$ (5)

式中p为次谐波级数。将上述由功率谱反演法和低频补偿法相加得到非Kolmogorov湍流相位屏。

2.2. 光斑漂移的贝叶斯估计

光斑漂移受机械振动、空气扰动等因素的影响，导致光斑漂移位置偏离中心位置。而这些因素的影响通常是随机的、独立的，因此光斑漂移量可以被视为一个随机变量。受大气湍流的影响，在接收端传感器上产生测量误差 [17] 。由于漂移的随机性，导致无法确定光斑准确位置，因此需要估计光斑漂移位置。

光斑位置通常用光束在垂直传播方向上的相位屏x和y两个方向描述。假设漂移在x、y方向相互独立，先对x方向漂移量进行求解，在求y方向漂移量。通常漂移量在中心位置出现的频率高，远离中心的值出现的频率逐渐减少，因此可以选取正态分布作为漂移量的先验分布。文献 [5] 基于贝叶斯定理在正态假设下研究了Kolmogorov湍流激光光斑漂移特性。

分析光斑在x方向上漂移，在时刻t有观测值 $b_x\left(t\right)$ 和真实值 $a_x\left(t\right)$ ，满足

$b_x\left(t\right)=a_x\left(t\right)+\omega$ (6)

式中 $\omega$ 为测量误差服从零均值，方差为 ${\sigma }^2$ 的高斯分布。

$a_x\left(t\right)$ 的先验分布为：

$p\left(a_x\left(t\right)\right)=\frac{1}{\sqrt{2\pi }{\sigma }_x}\exp \left[-\frac{1}{2{\sigma }_x^2}{\left(a_x\left(t\right)-{\mu }_x\right)}^2\right]$ (7)

上式 $a_x\left(t\right)$ 服从均值为 ${\mu }_x$ ，方差为 ${\sigma }_x$ 的正态分布。本文假设光斑中心位置在 $\left(0,0\right)$ 。

由(6)式求得似然函数：

$p\left(b_x\left(t\right)|a_x\left(t\right)\right)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left[-\frac{1}{2{\sigma }^2}{\left(b_x\left(t\right)-a_x\left(t\right)\right)}^2\right]$ (8)

根据贝叶斯定理， $a_x\left(t\right)$ 的后验密度为：

$\begin{array}{c}p\left(a_x\left(t\right)|b_x\left(t\right)\right)=\frac{p\left(b_x\left(t\right)|a_x\left(t\right)\right)p\left(a_x\left(t\right)\right)}{p\left(b_x\left(t\right)\right)}\propto p\left(b_x\left(t\right)|a_x\left(t\right)\right)p\left(a_x\left(t\right)\right)\\ \propto \frac{1}{\sqrt{2\pi }\sigma }\exp \left[-\frac{1}{2{\sigma }^2}{\left(b_x\left(t\right)-a_x\left(t\right)\right)}^2\right]\frac{1}{\sqrt{2\pi }{\sigma }_x}\exp \left[-\frac{1}{2{\sigma }_x^2}{\left(a_x\left(t\right)-{\mu }_x\right)}^2\right]\\ \propto \frac{1}{2\pi \sigma {\sigma }_x}\exp \left[-\frac{1}{2{\sigma }^2}{\left(b_x\left(t\right)-a_x\left(t\right)\right)}^2-\frac{1}{2{\sigma }_x^2}{\left(a_x\left(t\right)-{\mu }_x\right)}^2\right]\\ \propto \frac{1}{2\pi \sigma {\sigma }_x}\exp \left[-\frac{1}{2}\left(\frac{1}{{\sigma }^2}+\frac{1}{{\sigma }_x^2}\right)a_x{\left(t\right)}^2+\left(\frac{b_x\left(t\right)}{{\sigma }^2}+\frac{{\mu }_x}{{\sigma }_x^2}\right)a_x\left(t\right)-\frac{1}{2}\left(\frac{b_x{\left(t\right)}^2}{{\sigma }^2}+\frac{{\mu }_x^2}{{\sigma }_x^2}\right)\right]\\ \propto \frac{1}{2\pi \sigma {\sigma }_x}\exp \left\{-\frac{1}{2}\frac{{\sigma }_x^2+{\sigma }^2}{{\sigma }^2{\sigma }_x^2}\left[a_x{\left(t\right)}^2-2\left(\frac{b_x\left(t\right){\sigma }_x^2+{\mu }_x{\sigma }^2}{{\sigma }_x^2+{\sigma }^2}\right)a_x\left(t\right)+{\left(\frac{b_x\left(t\right){\sigma }_x^2+{\mu }_x{\sigma }^2}{{\sigma }_x^2+{\sigma }^2}\right)}^2\right]\right\}\end{array}$ (9)

从而 $a_x\left(t\right)$ 的后验分布：

$a_x\left(t\right)|b_x\left(t\right)~N\left(\frac{b_x\left(t\right){\sigma }_x^2+{\sigma }^2{\mu }_x}{{\sigma }_x^2+{\sigma }^2},\frac{{\sigma }^2{\sigma }_x^2}{{\sigma }^2+{\sigma }_x^2}\right)$ (10)

于是使用 $a_x\left(t\right)$ 的后验均值 $\frac{b_x\left(t\right){\sigma }_x^2+{\sigma }^2{\mu }_x}{{\sigma }_x^2+{\sigma }^2}$ 作为漂移量的估计值。

同理，y方向后验分布为：

$a_y\left(t\right)|b_y\left(t\right)~N\left(\frac{b_y\left(t\right){\sigma }_y^2+{\sigma }^2{\mu }_y}{{\sigma }_y^2+{\sigma }^2},\frac{{\sigma }_y^2{\sigma }^2}{{\sigma }_y^2+{\sigma }^2}\right)$ (11)

其中 $a_y\left(t\right)$ 为t时刻y方向光斑漂移量的真实值， $b_y\left(t\right)$ 为光斑漂移量的测量值。

3. 仿真实验与分析

分析湍流强度、幂律、传输距离和相位屏数量对漂移估计结果的影响。数值模拟高斯光束在非Kolmogorov湍流传输过程。相位屏网格大小 $N\times N=512\times 512$ 、间距 $\Delta z=100\text{m}$ ，波长 $\lambda =532\text{nm}$ ，功率谱反演法生成100张光斑图像，采样间隔1 s。

为了得到光斑漂移量，需要对光斑图像进行定位得到质心位置，常用的方法为形心定位法 [15] 和灰度重心法 [18] 和圆拟合法 [19] 。由于圆拟合抗干扰能力差，因此本文首先比较形心定位法和灰度重心法，再选择效果较好的方法作为本节模拟的定位方法。通过光斑定位图和平均绝对误差(Mean Absolute Error, MAE)来比较两种定位方法的准确性。在光斑图像中，越靠近质心中点，定位效果越好；MAE较小的定位效果越好。对100张光斑图像使用两种方法进行定位，得出形心定位法效果较好，其中1张定位图见图2。从图2可以看出，形心定位法相较于灰度重心法更接近图像高亮位置，高亮处为光斑中心位置，因此形心定位法得到的质心坐标较为准确。然后在强、中、弱三种湍流强度下对比两种方法的MAE，每种情况下随机模拟100张图像，定位后求得MAE见表1。由表1可以看出形心定位法的定位比较准确，误差较低，因此本节实验模拟数据采用形心定位法对光斑图像进行定位。

Figure 2. Spot location map

图2. 光斑定位图

Table 1. Comparison of MAE values of spot positioning by centroid positioning method and gray center of gravity method

表1. 形心定位法和灰度重心法光斑定位MAE值对比

首先，湍流强度和幂律是光束在影响非Kolmogorov湍流传输产生光斑漂移的重要因素。湍流强度越大，大气中的折射率变化越剧烈，从而导致光斑的扩散和漂移更加明显。分析湍流在 $C_n^2=4.2e^{-12}$ 、 $C_n^2=4.2e^{-14}$ 、 $C_n^2=4.2e^{-18}$ 分别为强、中、弱湍流情况下，研究了湍流强度对漂移估计值的影响。图3反映湍流强度对估计值的影响，在弱湍流情况下，光斑的位置变化相对较小，光斑漂移真实值的估计误差较小；随着湍流强度增大，x、y方向上的漂移估计值迅速偏离测量值，估计误差增大。

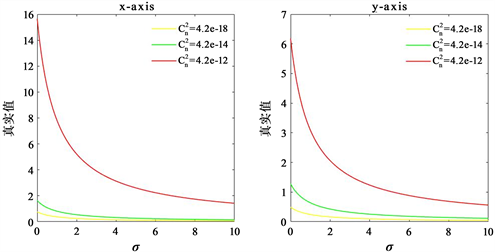
Figure 3. Drift estimates as a function of turbulence intensity

图3. 漂移估计值随湍流强度变化曲线

分析幂律对漂移估计值的影响，幂律的取值表示不同的湍流强度。非Kolmogorov大气湍流功率谱幂律在区间 $\left(3,5\right)$ 内变化，为了保证结构函数的连续性，通常将其限定在 $\left(3,4\right)$ 范围内。下面研究不同幂律取值对漂移估计值的影响。图4和图5分别显示了当幂律 $\alpha =3.1$ 和 $\alpha =3.9$ 时，高斯光束在非Kolmogorov湍流中传播后随机采样的100个质心的散点图，可以看出，随着功率谱幂律增大，光斑位置偏离中心位置，漂移效应越明显。对中等湍流强度下，分析不同幂律下x、y方向的漂移估计值。从表2可以看出，随着功率谱幂律 $\alpha$ 的增大光束的漂移量先增大后减小再增大，幂律小于11/3时，随着幂律的增大，光斑漂移量逐渐增大；幂律大于11/3时，随着幂律的增大，光斑漂移量先减小后增大，极大值点出现在 $\alpha =11/3$ 附近。

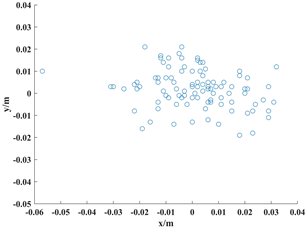
Figure 4. 100 centroid scatterplots were randomly sampled at $\alpha =3.1$

图4. $\alpha =3.1$ 时随机抽样100个质心散点图

Figure 5. 100 centroid scatterplots were randomly sampled at $\alpha =3.9$

图5. $\alpha =3.9$ 时随机抽样100个质心散点图

Table 2. Comparison of MAE values between the posterior estimation method and the MA method

表2. 后验估计方法和MA方法的MAE值对比

其次，传输距离和相位屏数量对光斑漂移也产生一定的影响。由于传输距离的增加，会导致传播路径中包含大尺度涡旋和折射率变化，使大气湍流变得更复杂，因此需要分析传输距离对光斑漂移的影响。在 $C_n^2=4.2e^{-14}$ ，传输距离为200 m、500 m、1000 m、1500 m、2000 m时，分析不同传输距离对x方向和y方向漂移估计误差的影响。图6反映了当传输距离较近时，高斯光束受涡旋影响较小，光斑漂移量的估计误差较小；当传输距离较远时，高斯光束受到更多的湍流扰动，大气湍流引起的光斑漂移现象更加明显，导致估计误差增大。

Figure 6. The drift estimation error varies with the transmission distance

图6. 漂移估计误差随传输距离变化曲线

相位屏模拟本身具有随机性，仅研究光束通过单相位屏后的光斑漂移量不能反映整个传输过程后的光束质量，因此需要进行多相位屏的模拟。在相同条件下模拟高斯光束通过不同相位屏数量的光斑漂移现象，图7可以发现当采用的相位屏数量较少时，估计误差较大。在传输模拟过程中，相位屏数量的选取对模拟得到的光束漂移的结果有影响，当相位屏数量较多时，估计精度提高，在模拟过程应该选择合适的相位屏数量，已降低湍流对漂移的影响。通过使用多个相位屏，可以模拟系统中的不确定性和随机性，更全面地考虑光束在非Kolmogorov湍流传输情况。

Figure 7. The effect of the number of phase screens on spot drift estimation

图7. 相位屏数量对光斑漂移估计的影响

最后分析后验估计模型的估计性能。由图8得，观测值与真实值之间的差异很小且趋势一致，认为该模型估计精度较高。接着将本文提出的后验模型估计方法与文献 [20] 中的MA模型进行对比。在中等湍流情况下x、y方向的MAE见表3。可以看出本文所提出的方法MAE较低，因此本文的方法可以更准确的估计漂移量。

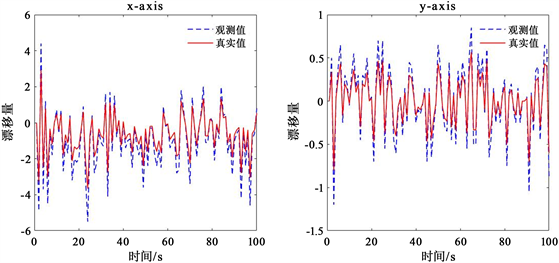
Figure 8. Visual analysis of model accuracy

图8. 模型准确性可视化分析

Table 3. Comparison of MAE values of posterior estimation method and MA method

表3. 后验估计方法和MA方法的MAE值对比

4. 结论

本文研究了非Kolmogorov湍流中激光光斑漂移的统计模拟，给出了相位屏的生成、质心定位和漂移量估计的一般框架。产生相位屏时，利用低频补偿法弥补功率谱反演法低频不足的缺点。质心定位时，模拟比较了形心定位法和灰度重心法，建议以后的研究中采用平均绝对误差较小的形心定位法。漂移量的估计时，推导了非Kolmogorov湍流中激光光斑漂移的贝叶斯估计方法。通过统计模拟分析了湍流强度、传输距离、幂律、相位屏等对漂移的影响。实验结果表明：x、y方向的漂移量受湍流强度和传输距离的增加而增大，漂移估计精度降低；漂移量随幂律的增大呈先增大后减小再增大趋势；相位屏数量增多时，漂移估计误差减小；与MA模型相比，光斑漂移量的贝叶斯估计方法的平均绝对误差较小，估计效果较好。本文对光斑漂移的研究还是基于各向同性湍流，只是其功率谱幂律偏离Kolmogorov湍流的幂律，在之后的非Kolmogorov湍流研究中应该考虑各向异性因子对光斑漂移的影响。

基金项目

吉林省教育厅项目(JJKH20210809KJ)、国家自然科学基金面上项目(12271271)。

NOTES

^*通讯作者。