1. 引言
多准则决策(multi-criteria decision making, MCDM)是一个框架,它通过基于众多标准对一组预先确定的备选方案进行评估,从而促进从这些备选方案中选择最合适的方案。对多准则决策方法进行系统深入的研究对于解决实际问题具有重要的意义。其中TOPSIS (Technique for Order Preference by Similarity to Ideal Solution)法具有直观的几何意义,应用范围广,是一种有效的多属性决策方法 [1] 。TOPSIS根据理想解与备选解的相似性进行排序,现已广泛应用于绿色低碳港口评价 [2] 、制造系统流程 [3] 、解决方案选择 [4] 、绿色供应链管理 [5] 等领域。
在TOPSIS计算过程中,评价数据通常是确定性值。然而,在实际决策领域,由于评估标准固有的模糊性和专家评级的主观性,获取确定性数据具有挑战性。为了解决这些问题,在TOPSIS方法中引入了模糊集理论,该理论可以通过使用模糊数学来表示语言概念。在当代研究中,许多模糊集理论已被纳入TOPSIS方法,如模糊集 [6] ,直觉模糊集 [7] ,毕达哥拉斯模糊集 [8] ,区间值三角形模糊集 [9] ,区间值直觉模糊集 [10] 。在这些传统的模糊逻辑模型中,将语言概念转化为隶属函数,并构建计算框架来进行评价过程。模糊集理论在一定程度上考虑了评价的模糊性,但在实际评价过程中,专家意见的分歧引入了一定程度的随机性。因此,本文引入隶属云模型和毕达哥拉斯模糊集来构造毕达哥拉斯模糊云-TOPSIS混合模型。
在现代高科技战场上,装备种类繁多,内部结构复杂,这使得装备的损坏率和维修难度显著提高。军队装备的维修保障能力是维持和恢复装备性能、保障战斗力持续生成的重要因素 [11] 。高效科学的维修保障是取得战争胜利的关键因素,而提高维修保障能力,实施装备维修保障能力评估工作,是装备维修质量得以保证的前提 [12] 。本文对装备维修保障环节中的野战修理所选址决策进行能力评估,来验证所提出的毕达哥拉斯模糊云-TOPSIS混合模型的可行性和科学性。
2. 构建野战修理所选址评估指标体系
抢修分队的战场应急抢修作业是战时装备保障任务的重要环节。抢修小组的具体位置会影响到任务的及时性和单位的安全性。抢修分队需要在接到上级命令后,在规定时间内合理分配设备和人员任务。科学合理的野战修理所选址,不仅可以保证维修支队的安全和隐蔽性,而且可以保证设备维修的效率,使战斗损坏的设备尽快投入战场使用。
根据构建指标体系的原则,本文从隐蔽性、土地、基础设施、交通和环境五个维度构建野战修理所选址评估指标体系,见图1。

Figure 1. Block diagram of the evaluation index system for the site selection of field repair stations
图1. 野战修理所选址评估指标体系框图
2.1. 隐蔽性
隐蔽是为了在战时躲避敌人的侦察和攻击,保障我军装备的维修,维持一线战斗力。抢修现场周围的植被为工作提供了一个相对隐蔽的场所。同时,与敌方侦察机和火力攻击点的距离,可以有效避开敌人的火力攻击,保证我方人员的安全。
2.2. 土地
为了便于装备维修作业的部署,要求现场维修站具备一定的规模。同时,土地成本也在考虑范围之内,旨在最大限度地减少军费开支。此外,需要进一步调查评估该地区的施工难度,以确保有效完成维修作业。
2.3. 基础设施
Tianci [13] 提出技术战备能力是装备保障能力的重要指标。技术准备的质量是根据其配套设施的可行性和环境的适宜性来评价的。野战修理所是战场后勤保障技术的集中场所。我们要确保他们的基础设施能够提供适当的工作条件。
2.4. 运输
Sennaroglu [14] 等人提出了基于基础设施的污水系统、通信网络状况、能源网络状况和交通网络状况四个子指标,用于军用机场选址评价。由于现场修理所对污水的需求量较小,本文未考虑污水系统指标。
2.5. 环境
在考虑选址现场维修站的环境时,应考虑以下因素:气候条件、社会条件和周围环境。注意避免极端天气或高温造成设备损坏。此外,应该尽量减少对附近居民生活质量的影响。决策者在进行选址时需要考虑周边地区的整体情况。
3. 基于博弈论的组合权重确定
主客观结合的加权方法根据数学原理可分为线性加权法和乘法综合法两类。线性加权法在一定程度上克服了乘法加权法带来的权重放大问题,具有较好的适用性。因此,本研究首先采用层次分析法和熵权法来获得主客观权重。为了更好地分配主客观权重的系数值,本文引入博弈论来计算系数 [15] 。
3.1. 层次分析法
层次分析法(Analytic Hierarchy Process, AHP)是MCDM方法的一种,最早由Thomas L. Saaty教授于1977年提出。它通过将复杂问题分解为层次,对潜在的指标进行比较,以加权每个因素,并给出一致性比率。
假设评估对象受到n个指标因素影响,表示为
。对同一层级的指标
与指标
的相对重要性进行比较,记作
,采用1~9标度法,构造判断矩阵
。将判断矩阵归一化后按列求和,可以得到主观权重
。最后通过一致性检验来验证权重的科学性,
(1)
式中:n表示判断矩阵的阶数,
表示矩阵的最大特征根。RI表示随机一致性检验,可以对一致性指标进行修正。若相对一致性指标
时,认为该判断矩阵满足一致性要求。若
,则需要调整判断矩阵直至满足一致性检验为止。
3.2. 熵权法
熵是一个热力学概念,通常与系统内的无序、随机性或不确定性水平有关。熵权法是一种客观的权重计算方法,有助于避免权重设置的主观性。
首先,需要对原始评价数据矩阵
进行正向化和标准化后构成数据矩阵
,确保这些数据达到一致的维度。其中X表示原始评价矩阵,
表示指标值,m为待评价的方案个数,n表示评价指标数。
接下来,计算第j项指标熵值。
(2)
最后,计算客观权重。
(3)
其中,
为第j项指标差异性系数。若某个指标的信息熵越小,说明该指标值的变异程度越大,所提供的信息量也越大,认为该指标对综合评价的作用也越大,反之亦然。
3.3. 基于博弈论的组合赋权法
根据所获得主观权重
和客观权重
,组合权重W的线性加权表达式如下,
(4)
其中
分别表示主客观权重的线性组合系数。
结合博弈论思想,采用偏差最小化法对线性组合系数进行了优化。根据W和每个
的偏差最小化原则,对组合系数进行优化,得到目标函数和约束条件如下,
(5)
根据微分原理进行求导,
(6)
通过求解上式可得到最优组合系数,通过归一化计算得到最终的综合权重,如下,
(7)
4. 基于毕达哥拉斯模糊云的评估模型构建
4.1. 毕达哥拉斯模糊集
模糊集合理论是由Zadeh于1965年提出的,作为处理数据和信息中的不确定性。该理论的基础是允许研究对象在0和1之间连续变化的程度上属于一个集合,而不是简单地属于或不属于这个集合。实现对概念及其关系更细致和灵活的表示,在从工程和计算机科学到经济学和心理学的各个领域都有应用。Atanassov [16] 在1986引入了非隶属性的概念,并在模糊集的基础上提出了直觉模糊集(Intuitionistic fuzzy sets, IFS),从肯定、否定和犹豫三个角度描述信息。这使得模糊信息的处理更普适,更符合人们的思维和行为方式。
Yager [17] 2013年提出了毕达哥拉斯模糊集(Pythagorean fuzzy sets, PFS),作为传统模糊集的扩展来有效处理不确定性,扩大了模糊集的约束范围。假设全称集合X上的一个毕达哥拉斯模糊集P可以描述为,
(8)
其中
和
表示隶属度和非隶属度,满足
和
。犹豫度可以表示为
。
根据PFS运算法则,毕达哥拉斯模糊距离可表示为,
(9)
4.2. 云模型
李德毅 [18] 提出了一种新的认知模型,称为“云模型”,它可以有效地捕捉概念固有的随机性和模糊性,并促进定性概念向定量表征的转化,考虑到过程中的不确定性。给定U为精确数值表示的定量域,则T是U上的定性概念。如果定量值为
,x是定性概念T的随机实现,则x对概念T的确定性用
表示,如下,
(10)
期望(Ex)、熵(En)和超熵(He)是云模型的基本数值特征。Ex表示云滴在集合中的预期分布。En与定性概念的不确定性的量化有关。He表示熵的熵,是En的不确定度量,也间接反映了云的厚度,超熵越大,云滴离散度越大,这可以通过隶属度的随机波动和云滴来证明 [19] 。图2为1500个云滴的
云图。
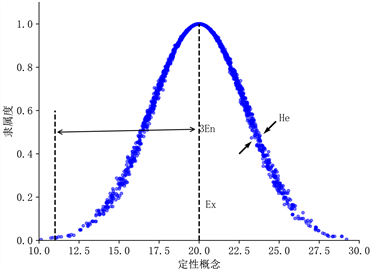
Figure 2. Schematic diagram of the cloud model
图2. 云模型示意图
评价指标根据性质可以分为定量指标和定性指标。对于定量指标,可以通过下式计算出隶属云数值特征,
(11)
对于定性指标,我们采用黄金分割线的方法确定其隶属云数值特征。本文将评估等级分为“优秀、良好、中等、较差、差”五个等级,通过黄金分割法得到的云数值特征,见表1。

Table 1. Numerical characteristics of the cloud were evaluated on a scale
表1. 等级评价云数值特征
本文给出云模型中隶属云之间的距离公式,若两朵云为
,
,根据云模型运算法则,两者的距离如下,
(12)
4.3. 毕达哥拉斯模糊云
Zhang等人 [20] 提出云模型中的Ex表示为毕达哥拉斯模糊数
。因此,推导出毕达哥拉斯模糊云(Pythagorean fuzzy cloud, PFC)的表达式为
。并且,PFC的确定性程度可以表示为,
(13)
式中,y为PFC的确定性程度,
为隶属度
与非隶属度
相关的PFC调整系数,其取值范围在
区间内。
假设两朵毕达哥拉斯模糊云分别表示为
,
,其距离测度公式可以表示为,
(14)
其中
,
,
,
。
(15)
(16)
(17)
4.4. PFC-TOPSIS
C.L. Hwang [21] 首先提出了TOPSIS,认为其是解决多准则决策问题的有效方法。TOPSIS是一种多标准技术,用于通过同时最小化到理想点的距离和最大化到最低点的距离来从有限的备选集中识别最佳方案。
根据决策评价对象构建的评价指标体系包含m个评价指标,并选择n个备选决策方案。根据专家意见,可以形成决策矩阵
。对决策矩阵进行标准化得到矩阵
,保证各指标得分在同一维度,避免因维度差异造成的评价误差。
本文引入加权算术平均算子,得到毕达哥拉斯模糊云加权算术平均算子(Pythagorean fuzzy cloud weighted arithmetic average, PFCWAA),进行指标加权。式(15)为综合权重对各指标进行加权的表达式。对标准化后的矩阵进行加权可以得到指标矩阵
。结合TOPSIS法,通过式(16)可以确定最佳综合云和最差综合云。通过式(17)计算各备选方案与正、负理想云之间的距离,并计算各方案的贴近度。最后,根据方案的接近程度对方案进行排序。贴近度越高,说明方案越好。
5. 实例
5.1. 确定指标权重
首先根据专家对指标的重要性程度判断情况计算主观权重,根据仿真行动评估数据计算客观权重,计算结合博弈论得到最后的综合权重,具体数值结果见表2。

Table 2. Comparison table of indicator weights
表2. 指标权重对比表
表中可以看出交通的权重值最大,其次为基础设施、隐蔽性、土地、和环境。说明交通对于选址决策的影响程度最大。这也进一步验证了抢修过程中,抢修效率会在很大程度上影响其抢修结果。子指标中,交通便捷性的指标权重值最大,其次为防御能力,通信网络状况,能源情况,和与主干道的距离。片区周边状况对选址决策的影响程度较小。结合博弈论对主客观权重都进行了修正,增强了权重的说服性。
5.2. 评估结果
首先,根据专家对各子指标的评价数据,计算各指标的隶属云数值特征。通过正向云生成器可以得到各指标的云图。然后,根据期望的指标权重,对指标进行集成,得到准则层的隶属云数值特征,如图3(a)~(e)所示。
根据准则层指标权重进行加权,可以得到每个决策方案的综合云数值,通过正向云发生器得到图3(f)的云图,可以对各方案进行一个初步排序。
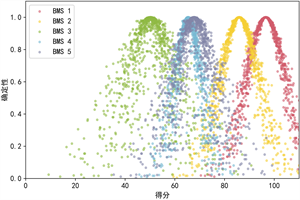

(a) 隐蔽性 (b) 土地

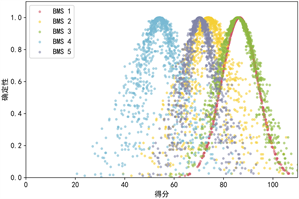 (c) 基础设施 (d) 交通
(c) 基础设施 (d) 交通
 (e) 环境 (f) 综合云
(e) 环境 (f) 综合云
Figure 3. Site selection decision evaluation criteria cloud and synthetic cloud
图3. 选址决策评估准则云和综合云
通过式(16),得到正理想解和负理想解,计算备选解与正理想解和负理想解的距离和贴近度。最终结果如表3所示。根据贴近度值,选址决策从最优到最劣的排名依次为BMS1、BMS3、BMS5、BMS2、BMS4,这与PFC计算得到的结果是一致的。其中,BMS1的贴近度为0.9758,表明它非常接近正理想解,可以认为是一个相对理想的解。

Table 3. The proximity and ranking of each site selection scheme
表3. 各选址方案贴近度及排名情况
最后对专家提供的每组解决方案的评价结果进行分析。在BMS1选择的情况下,与前线部队的距离获得较低的分数,而其他标准的分数则为良好或以上。根据权重表,与前线部队的距离权重仅为0.0543,这表明对整体决策过程的影响相对较小。对于BMS2来说,土地价格被认为不合理,通讯网络和能源供应的状况也不理想。此外,场地远离前线部队和主干道,对设备维修和运输作业的效率产生了负面影响。对于BMS3而言,主要是由于场地附近植被条件差,与明显目标的距离较近,导致场地隐蔽性降低,容易受到敌人的攻击和侦察,从而影响野战修理所的安全性。BMS4在土地规模、通讯等方面的评分均较低,同时距离主干道的距离较远。隐蔽性和运输性得分都比较低,说明该决策在各方面还需要进一步改进。BMS5主要需要在水文条件、与明显目标、前线部队、主干道的距离等方面进行改进。
5.3. 对比验证
为了验证本研究中提出的方法的科学性,使用层次分析法、云模型和TOPSIS法进行了对比实验,评估结果见表4。

Table 4. Comparison of different assessment methods
表4. 不同评估方法的对比结果
层次分析法是决策中最基本、最有效的方法。基于案例研究,获得的决策方案综合得分分别为89.55、64.76、84.59、60.33和79.76。TOPSIS是另一种常用的MCDM方法。通过结合给定情况计算每组备选方案的贴近度,确定各方案的贴近度分别为0.3368、0.2054、0.1536、0.1621和0.1422。云模型可以有效地处理评价过程中的随机性和模糊性。可以得到各备选方案的综合云数值特征如下:
、
、
、
、
。
表4中每种方法得到的最终结果一致,证实了PFC-TOPSIS评估模型的科学性和可靠性。AHP在评价过程中容易出现主观判断和歧义,导致评价结果客观性较低。在TOPSIS中,每个备选方案的区分能力很低,当多个备选方案具有相似的属性得分时,区分备选方案的能力较弱。综上所述,通过对比实验和数值结果分析,验证了所提方法的可靠性和鲁棒性。
6. 结论
1) 基于仿真条件下野战修理所选址决策的实际情况,选取隐蔽性、土地、基础设施、交通和环境作为评估指标的准则层,利用层次分析法和熵权法确定主客观权重,并采用博弈论思想进行组合赋权,构建野战修理所选址决策评价指标模型。
2) 利用毕达哥拉斯模糊集和云模型耦合,构建毕达哥拉斯模糊云,采用TOPSIS法度量决策的贴近度,构建毕达哥拉斯模糊云-TOPSIS的混合评价模型。
3) 针对仿真条件下五组选址决策进行评估,并选用常用的层次分析法、TOPSIS法和云模型进行实验对比,验证了本文所提方法模型的可靠性和鲁棒性。不同评估方法选择的最优选址决策均为BMS1,并且本文所提出的PFC-TOPSIS法更好地描述了评价中的模糊性和随机性,具有一定的科学意义。
基金项目
2022年江苏省研究生科研与实践创新计划项目(SJCX22_0245、SJCX22_0248、KYCX22_0897)。
NOTES
*通讯作者。