基于割方法的一类n-维全苯类多环芳香烃PBAHs(n)的分子拓扑特征研究

Research on Topological Indices of n-Dimension Polycyclic Aromatic Hydrocarbons Based on Cut Methods

摘要: 化合物分子的拓扑指标是一种分子图的数值不变量，也被称为分子结构描述符，它在理论化学中被用于量子结构性质关系(QSPR)与量子结构活性关系(QSAR)的设计。大型多环芳香烃(PAHs)是指由碳和氢原子所组成的苯类化合物。化学上，大型多环芳香烃包含至少两个苯环并以线性、簇、或角状排列的方式存在，而全苯类多环芳香烃(PBAHs)是一种特殊的多环芳香烃。本文利用化合物分子图中的Djoković-Winkler关系，构造相应的商图，采用割方法给出了一类n-维全苯类多环芳香烃(PBAHs(n))的十三种拓扑指标的具体表达式。

Abstract: The topological index of compound molecule is a numerical invariant of a molecular graph, also known as molecular structure descriptor, which is used in theoretical chemistry for the design of quantum structural property relationship (QSPR) and quantum structure activity relationship (QSAR). Large polycyclic aromatic hydrocarbon (PAHs) is a compound composed of carbon and hy-drogen atoms. Chemically, large polycyclic aromatic hydrocarbons contain at least two benzene rings and exist in a linear, cluster, or angular arrangement, while the total benzene polycyclic aro-matic hydrocarbon (PBAHs(n)) is a special polycyclic aromatic hydrocarbon. In this paper, we give the explicit expressions of thirteen topological indices of n-dimensional total benzene polycyclic aromatic hydrocarbon (PBAHs(n)), based on the Djoković-Winkler of the molecular graphs and its corresponding quotient graphs.

1. 介绍

多环芳香烃(PAHs)是一种强有机化合物，它通常为无色、白色或淡黄色固体。它们是数百种化学相关化合物的集合，通过不同的活动对生物体产生不同的毒性。化学上，大型多环芳香烃包含至少两个苯环并以线性、簇、或角状排列的方式存在，而全苯类多环芳香烃(PBAHs)是一种特殊的多环芳香烃。多环芳香烃的总体物理性质是具有高熔点、沸点、低烟压和低流体溶解度。同时，多环芳香烃在天然溶剂中可溶解，因为它们具有异常的亲脂性。多环芳香烃同样表现出不同的能力，例如：光的可影响性、热对抗、电导率、辐射能力、抗侵蚀性和生理活性等。它们大多被用作药品、农业物品、摄影物品、热固性塑料、润滑材料和其他化合物企业的中间产品 [1] 。多环芳香烃的化学和生物学特性取决于它们的结构和隐藏的分子拓扑结构。在此基础上，定量结构–活性关系(QSAR)，和定量结构–性质关系(QSPR)，策略用于从多环苯类化合物的结构预测其性质和相关图 [2] - [7] 。正是由于多环芳香烃在石油工业、化学制造和制药企业中的广泛应用，所以它的化学和生物活性具有重要的意义。因此，它们的毒性、致癌性和皮肤浸润性等都受到了学者的高度关注。超芳香族稳定能(SSE)可以用来表征非常大的多环芳香烃(PAHs)中单个苯环的局部芳香度指标。利用QSAR和QSPR策略可以从这些化合物的结构中预测它们的大量可感知性质和可能的毒性 [8] 。大型多环芳香烃(PAHs)可以看作是石墨烯的分子亚基。到目前为止，许多大型多环芳烃已经被设计用于探索纳米石墨烯可能的电子结构特性以及其他相关性质 [9] 。

从图论的角度看，苯类系统指的是无割点的有限连通可平面图。苯类系统属于苯并类碳氢化合物，它具有迷人的、在某种程度上甚至奇怪的电子性质，150多年来一直受到理论化学家们的高度关注。此外，它们是化工行业的重要原材料，例如：用于制造颜色和塑料。最近对石墨烯基纳米管和纳米材料的兴趣，同样激发了对多环苯类化合物的进一步研究的兴趣。多环芳香烃(PAHs)是一种特殊的苯类系统。

全苯类的多环芳香烃(PBAHs)由于分子间和与表面或模板的相互作用，已取代和未取代的(PBAHs)可以在2维和3维上自组装而形成。自组装的单分子层可以沉积在各种表面上，从本质上可以产生二维晶体。(PBAHs)富含电子的核特别适合通过扫描隧道显微镜(STM)进行可视化，给出提供二维晶格清晰地图的亮点。高热稳定性的大型未取代多环芳香烃(PBAHs) (如图1所示)，其高热稳定性允许在超高真空条件下，在550℃~650℃下进行部分升华 [10] 。

Figure 1. Graph PBAHs (2)

图1. 图PBAHs (2)

拓扑指标对应化学分子图的一个特定的拓扑元素，是化学分子图的一种数值描述符。这些拓扑指标是图论为化合物的假设学习提供的有价值的工具。拓扑指标的益处在于，它们可以在定量结构–性质关系(QSPR)和定量结构–活性关系(QSAR)中作为直接的数值描述符使用 [11] ，用于检查分子或原子的物理、化学或生物活性。随着研究的不断深入，拓扑指标不仅在化学、药物发现等领域，而且在铁路运输等复杂网络领域都有广泛的应用 [12] 。最广为人知的拓扑指标之一是以HaroldWiener命名的Wiener指标。一个图的Wiener指标 [13] 被定义为关联图中所有顶点对之间距离之和。由于Wiener指标可以很快计算出来，因此它很快在一段时间内得到了广泛的研究和讨论。通过研究表明，Wiener指标似乎与化合物的各种物理化学性质都存在一些关联，并在各个领域得到了应用，例如：晶体学、对应假设、鸟类学等。继Wiener指标之后，学者们又提出了几种基于距离的拓扑指标，它们具有不同的定量度量Schultz指标是一个基于度和距离的拓扑指标，具有重要的实际应用和性质 [14] ，其修正后的指标被称为Gutman指标 [15] 。Szeged指标及其不同的变式也广泛应用于描述分子结构中原子之间的相互关系。文献 [16] 给出了Wiener、PI和Szeged指标等拓扑指标与扶手型六面体型碳纳米管的电矩和能量之间的关系。PI指标在QSPR/QSAR研究中的应用已在文献 [17] 中得到验证。Mostar指标及其变式是最近提出的用于检查外围的度量结构的一种描述符 [18] 。文献 [19] 对某些苯类碳氢化合物的基于距离的拓扑描述符进行了质量测试。本文主要研究了一类基于距离的Clar型多环芳香烃(PBAHs(n))的拓扑描述符，如图2所示。

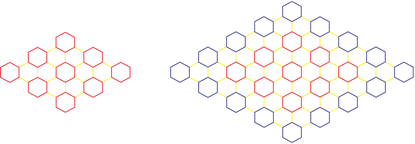
Figure 2. Graphs PBAHs (2) and PBAHs (3)

图2. 图PBAHs (2)和PBAHs (3)

本文利用化合物分子图中的Djoković-Winkler关系，构造相应的商图，采用割方法给出了一类n-维全苯类多环芳香烃(PBAHs(n))的十三种拓扑指标的具体表达式。

2. 预备知识

本文所研究的图都是无向、有限的简单图。令G表示一个顶点集为 $V\left(G\right)$ ，边集为 $E\left(G\right)$ 的分子图。与点 $v\in V\left(G\right)$ 相关联的边的条数称为顶点v的度，用 $d_G\left(v\right)$ 表示 $d_G\left(u\mathrm{,}v\right)$ 表示顶点u和v之间最短路的长度。用这种定义方式，顶点u到边 $f=xy$ 的距离，表示为 $d_G\left(u\mathrm{,}f\right)$ ，定义为 $\min \left\{d_G\left(u\mathrm{,}x\right),d_G\left(u\mathrm{,}y\right)\right\}$ ，而两条边 $e=uv$ 与 $f=xy$ 之间的距离，表示为 $D_G\left(e\mathrm{,}f\right)$ ，定义为 $\min \left\{d_G\left(u\mathrm{,}f\right),d_G\left(v\mathrm{,}f\right)\right\}$ 。对于一条边 $e\mathrm{<mo>\; =\; </mo>}uv\in E\left(G\right)$ ，分别用 $N_u\left(e\mathrm{<mo>\; |\; </mo>}G\right)$ 和 $M_u\left(e\mathrm{<mo>\; |\; </mo>}G\right)$ 表示图G中到点u的距离比到点v的距离更近的点和边的集合，其阶数分别记为 $n_u\left(e\mathrm{<mo>\; |\; </mo>}G\right)$ 和 $m_u\left(e\mathrm{<mo>\; |\; </mo>}G\right)$ 。类似地可以定义 $n_v\left(e\mathrm{<mo>\; |\; </mo>}G\right)$ 和 $m_v\left(e\mathrm{<mo>\; |\; </mo>}G\right)$ 。如果 $d_G\left(u\mathrm{,}v\right)=d_H\left(u\mathrm{,}v\right)$ ，那么图G的子图H称为是等距的，这种良好定义的超立方体的子图的集合称为部分超立方体。如果H中任意两个顶点之间的最短路完全都在H中，那么图G的子图H就称为是凸的。

当涉及基于距离的图不变量时，割方法是非常有用的，这是化学图论的核心思想之一 [20] [21] 。它是根据Djoković-Winkler关系 $\Theta$ ，给图G的边集的一个分配。这个关系 $\Theta$ 表述为：对于边集 $E\left(G\right)$ 的任意两条边 $e=uv$ 和 $f=xy$ ， $d_G\left(u\mathrm{,}x\right)+d_G\left(v\mathrm{,}y\right)\ne d_G\left(u\mathrm{,}y\right)+d_G\left(v\mathrm{,}x\right)$ 。这个关系 $\Theta$ 一般来说是满足自反性和对称性的，但是不满足传递性。但是如果对于部分超立方体来说，它是满足传递性的。关系 $\Theta$ 将图G的边集划分为 $F_1,F_2,\cdots ,F_r$ 类，也叫做 $\Theta$ -类或者割。事实上，它的传递闭包 ${\Theta }^{\mathrm{<mo>\; *\; </mo>}}$ 是一个等价关系，去掉每个类之后可以得到两个或两个以上的点分支。对于一个边集 $E\left(G\right)$ 的划分 $E=\left\{E_1\mathrm{,}{E}_2\mathrm{,}\cdots \mathrm{,}{E}_k\right\}$ ，如果说每个边集 $E_i$ 是一个或多个图G的 ${\Theta }^{\mathrm{<mo>\; *\; </mo>}}$ -类的并集，那么就称划分 $E$ 比划分 $F$ 更粗糙。对于任意的边集划分 $E_i$ ，商图 $G/E_i$ 是由不连通的图 $G\backslash E_i$ 构成的，其中连通分支作为顶点，两个连通分支 $C_j^i$ 与 $C_k^i$ 相邻，只要顶点 $x\in C_j^i$ 与顶点 $y\in C_k^i$ 有边 $xy\in E_i$ 。

加强赋权图 $G_{sw}=\left(G\mathrm{,}\left(w_v\mathrm{,}{s}_v\right)\mathrm{,}{s}_e\right)$ 最早在文献 [4] 中被提出，随后在文献 [6] [7] [18] 和 [22] - [27] 中进行广泛讨论。加强赋权图的顶点权值容量和顶点强度容量分别为 $w_v\mathrm{<mo>\; :\; </mo>}V\left(G_{sw}\right)\to {ℝ}_0^{+}$ ， $s_v\mathrm{<mo>\; :\; </mo>}V\left(G_{sw}\right)\to {ℝ}_0^{+}$ ，边强度容量 $s_e\mathrm{<mo>\; :\; </mo>}E\left(G_{sw}\right)\to {ℝ}_0^{+}$ 。在加强赋权图中，有 $d_{G_{sw}}\left(u\mathrm{,}v\right)=d_G\left(u\mathrm{,}v\right)$ ， $d_{G_{sw}}\left(u\mathrm{,}f\right)=d_G\left(u\mathrm{,}f\right)$ ， $D_{G_{sw}}\left(e\mathrm{,}f\right)=D_G\left(e\mathrm{,}f\right)$ ， $N_u\left(e\mathrm{<mo>\; |\; </mo>}{G}_{sw}\right)=N_u\left(e\mathrm{<mo>\; |\; </mo>}G\right)$ ， $M_u\left(e\mathrm{<mo>\; |\; </mo>}{G}_{sw}\right)=M_u\left(e\mathrm{<mo>\; |\; </mo>}G\right)$ ， $n_u\left(e\mathrm{<mo>\; |\; </mo>}{G}_{sw}\right)={\displaystyle \underset{x\in N_u\left(e\mathrm{<mo>\; |\; </mo>}{G}_{sw}\right)}{\sum }}{w}_v\left(x\right)$ ， $m_u\left(e\mathrm{<mo>\; |\; </mo>}{G}_{sw}\right)={\displaystyle \underset{x\in N_u\left(e\mathrm{<mo>\; |\; </mo>}{G}_{sw}\right)}{\sum }}{s}_v\left(x\right)+{\displaystyle \underset{f\in M_u\left(e\mathrm{<mo>\; |\; </mo>}{G}_{sw}\right)}{\sum }}{s}_e\left(f\right)$ 。而 $n_v\left(e\mathrm{<mo>\; |\; </mo>}{G}_{sw}\right)$ 和 $m_v\left(e\mathrm{<mo>\; |\; </mo>}{G}_{sw}\right)$ 可以类似定义。加强赋权图 $G_{sw}$ 中一个顶点u的度为 $d_{G_{sw}}\left(u\right)=2s_v\left(u\right)+{\displaystyle \underset{x\in N_{G_{sw}}\left(u\right)}{\sum }}{s}_e\left(ux\right)$ 。加强赋权图的其中一部分拓扑指标的定义，在文献 [5] 中已经(如表1所示)给出。此外，当 $w_v=1$ ， $s_v=0$ ， $s_e=1$ ， $w_e=1$ 时，有 $TI\left(G_{sw}\right)=TI\left(G\right)$ 。

Table 1. Topological indices for strength-weighted graph G s w

表1. 加强赋权图 $G_{sw}$ 的若干拓扑指标

定理1. [28] 对于 $G_{sw}=\left(G\mathrm{,}\left(w_v\mathrm{,}{s}_v\right)\mathrm{,}{s}_e\right)$ ，令 $E=\left\{E_1\mathrm{,}{E}_2\mathrm{,}\cdots \mathrm{,}{E}_k\right\}$ 是边集 $E\left(G\right)$ 的一个比 $F$ 更粗糙的划分，TI表示拓扑指标：W， $W_e$ ， $W_{ve}$ ， $S{z}_v$ ， $S{z}_e$ ， $S{z}_{ev}$ ， $S{z}_t$ ，PI，S， $Gut$ ， $Mo$ ， $M{o}_e$ 和 $M{o}_t$ 。则：

$TI\left(G_{sw}\right)={\displaystyle \underset{i=1}{\overset{k}{\sum }}}TI\left(G/E_i,\left(w_v^i,s_v^i\right),s_e^i\right),$

其中对于所有的连通分支 $C\in G/E_i$ ， $w_v^i:V\left(G/E_i\right)\to {ℝ}_0^{+}$ 定义为 $w_v^i\left(C\right)={\displaystyle \underset{x\in C}{\sum }}{w}_v\left(x\right)$ ， $s_v^i:V\left(G/E_i\right)\to {ℝ}_0^{+}$ 定义为 $s_v^i\left(C\right)={\displaystyle \underset{xy\in C}{\sum }}{s}_v\left(xy\right)+{\displaystyle \underset{x\in C}{\sum }}{s}_v\left(x\right)$ ， $s_e^i:E\left(G/E_i\right)\to {ℝ}_0^{+}$ 定义为边集 $E_i$ 中一端在连通分支C，而另一端在连通分支D的边的条数。

3. 主要结果

本节主要利用割方法来讨论多环芳香烃(PAHs)中的一类Clar型多环芳香烃(PBAHs(n))的几类拓扑指标。这类多环芳香烃有两个邻苯基的部分，它主要通过六边形分子的六个面构成的扶手型边所组成的，如图2和图3所示。

Figure 3. Graph PBAHs (4)

图3. 图PBAHs (4)

定理2. 令H₁是一个n维多环芳香烃(PBAHs(n))，则

(i) $W\left(H_1\right)=3\left(384n^5-1032n^4+1100n^3-582n^2+151n-12\right)\mathrm{<mo>\; ;\; </mo>}$

(ii) $W_e\left(H_1\right)=\left(15624n^5-54366n^4+76936n^3-55497n^2+20369n-2532\right)/6\mathrm{<mo>\; ;\; </mo>}$

(iii) $W_{ve}\left(H_1\right)=3\left(1160n^5-3574n^4+4430n^3-2765n^2+863n-88\right)/2\mathrm{<mo>\; ;\; </mo>}$

(iv) $S{z}_v\left(H_1\right)=3\left(6000n^6-20928n^5+30810n^4-24320n^3+10725n^2-2467n+180\right)/5\mathrm{<mo>\; ;\; </mo>}$

(v) $S{z}_e\left(H_1\right)=\left(81360n^6-344688n^5+624385n^4-618110n^3+350275n^2-106662n+10360\right)/10\mathrm{<mo>\; ;\; </mo>}$

(vi) $S{z}_{ev}\left(H_1\right)=\left(27180n^6-104856n^5+171930n^4-152725n^3+76710n^2-20369n+1710\right)/5\mathrm{<mo>\; ;\; </mo>}$

(vii) $S{z}_t\left(H_1\right)=\left(45216n^6-177936n^5+299393n^4-274986n^3+144293n^2-40588n+3656\right)/2\mathrm{<mo>\; ;\; </mo>}$

(viii) $PI\left(H_1\right)=2\left(675n^4-1874n^3+2008n^2-986n+149\right)\mathrm{<mo>\; ;\; </mo>}$

(ix) $S\left(H_1\right)=4\left(1740n^5-5136n^4+6091n^3-3630n^2+1079n-105\right)\mathrm{<mo>\; ;\; </mo>}$

(x) $Gut\left(H_1\right)=2\left(15624n^5-50316n^4+65872n^3-43863n^2+14792n-1707\right)/3\mathrm{<mo>\; ;\; </mo>}$

(xi) $Mo\left(H_1\right)=3\left(144n^4-336n^3+282n^2+2{\left(-1\right)}^{n}n-102n-{\left(-1\right)}^n+13\right)\mathrm{<mo>\; ;\; </mo>}$

(xii)

$M{o}_e\left(H_1\right)=\left(1260n^4+18{\left(-1\right)}^n{n}^3-3214n^3-84{\left(-1\right)}^n{n}^2+2952n^2+69{\left(-1\right)}^{n}n-1157n-20{\left(-1\right)}^n+160\right)/2\mathrm{<mo>\; ;\; </mo>}$

(xiii)

$M{o}_t\left(H_1\right)=\left(2124n^4+36{\left(-1\right)}^n{n}^3-5230n^3-84{\left(-1\right)}^n{n}^2+4644n^2+81{\left(-1\right)}^{n}n-1769n-26{\left(-1\right)}^n+238\right)/22.$

证明：显然，图H₁是由 $24n^2-24n+6$ 个顶点和 $36n^2-44n+14$ 条边组成。令 $\left\{A_{1i}\mathrm{<mo>\; :\; </mo>1}\le i\le n-1\right\}$ ， $\left\{{A^{\prime }}_{1i}\mathrm{<mo>\; :\; </mo>1}\le i\le n-1\right\}$ ， $\left\{A_{2i}\mathrm{<mo>\; :\; </mo>1}\le i\le n-1\right\}$ ， $\left\{{A^{\prime }}_{2i}\mathrm{<mo>\; :\; </mo>1}\le i\le n-1\right\}$ ， $\left\{A_{3i}\mathrm{<mo>\; :\; </mo>1}\le i\le n\right\}$ ， $\left\{A_{4i}\mathrm{<mo>\; :\; </mo>1}\le i\le n-1\right\}$ ， $\left\{B_{1i}\mathrm{<mo>\; :\; </mo>1}\le i\le 2n-2\right\}$ ， $\left\{{B^{\prime }}_{1i}\mathrm{<mo>\; :\; </mo>1}\le i\le 2n-2\right\}$ 和B是9种类型的灵敏割(acute cut)，其中 $A_{1i}$ 和 ${A^{\prime }}_{1i}$ ， $A_{2i}$ 和 ${A^{\prime }}_{2i}$ ， $B_{1i}$ 和 ${B^{\prime }}_{1i}$ 是同构的，如图4~7所示。商图 $H_1/A_{1i}$ ， $H_1/A_{2i}$ ， $H_1/A_{3i}$ ， $H_1/A_{4i}$ ， $H_1/B_{1i}$ 和 $H_1/B$ 分别是两个连通分支作为两个点的路，且它们的边强度容量分别为 $3i-1$ ， $3i$ ， $3n-1$ ， $3n-2$ ， $3i-1$ 和 $6n-4$ ，如图8所示。另外，顶点强度容量和顶点权值容量的值经过计算如表2所示。由于H₁的对称性，可以发现迟钝割(obtuse cuts)类似于灵敏割。因此，我们只计算了2次灵敏割，再加上水平方向的割来完成接下来的详细证明。

Figure 4. $\left\{A_{1i}\mathrm{<mo>\; :\; </mo>1}\le i\le 3\right\}$ , $\left\{{A^{\prime }}_{1i}\mathrm{<mo>\; :\; </mo>1}\le i\le 3\right\}$ , $\left\{A_{2i}\mathrm{<mo>\; :\; </mo>1}\le i\le 3\right\}$ and $\left\{{A^{\prime }}_{2i}\mathrm{<mo>\; :\; </mo>1}\le i\le 3\right\}$ cuts

图4. $\left\{A_{1i}\mathrm{<mo>\; :\; </mo>1}\le i\le 3\right\}$ ， $\left\{{A^{\prime }}_{1i}\mathrm{<mo>\; :\; </mo>1}\le i\le 3\right\}$ ， $\left\{A_{2i}\mathrm{<mo>\; :\; </mo>1}\le i\le 3\right\}$ 和 $\left\{{A^{\prime }}_{2i}\mathrm{<mo>\; :\; </mo>1}\le i\le 3\right\}$ 割

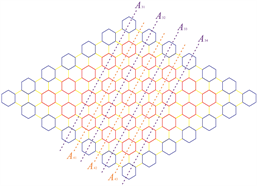
Figure 5. Two types cuts of $\left\{A_{3i}\mathrm{<mo>\; :\; </mo>1}\le i\le 4\right\}$ and $\left\{A_{4i}\mathrm{<mo>\; :\; </mo>1}\le i\le 3\right\}$

图5. $\left\{A_{3i}\mathrm{<mo>\; :\; </mo>1}\le i\le 4\right\}$ 和 $\left\{A_{4i}\mathrm{<mo>\; :\; </mo>1}\le i\le 3\right\}$ 两种割

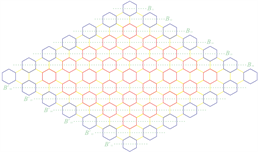
Figure 6. Two types of $\left\{B_{1i}\mathrm{<mo>\; :\; </mo>1}\le i\le 6\right\}$ cut

图6. $\left\{B_{1i}\mathrm{<mo>\; :\; </mo>1}\le i\le 6\right\}$ 型割

Figure 7. The type of B cut

图7. B型割

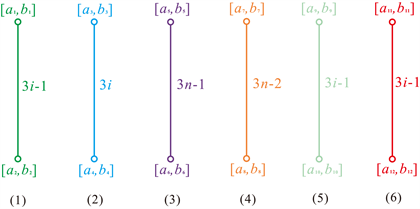
Figure 8. (1) $H_1/A_{1i}$ ; (2) $H_1/A_{2i}$ ; (3) $H_1/A_{3i}$ ; (4) $H_1/A_{4i}$ ; (5) $H_1/B_{1i}$ ; (6) $H_1/B$

图8. (1) $H_1/A_{1i}$ ；(2) $H_1/A_{2i}$ ；(3) $H_1/A_{3i}$ ；(4) $H_1/A_{4i}$ ；(5) $H_1/B_{1i}$ ；(6) $H_1/B$

Table 2. Vertex strength weighted values for acute cuts of PBAHs(n)

表2. PBAHs(n)在割方法下的顶点强度容量和顶点权值容量

$W\left(H_1\right)=2\left[2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}{a}_1{a}_2+2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}{a}_3{a}_4+{\displaystyle \underset{i=1}{\overset{n}{\sum }}}{a}_5{a}_6+{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}{a}_7{a}_8\right]+2{\displaystyle \underset{i=1}{\overset{2n-2}{\sum }}}{a}_9{a}_{10}+a_{11}{a}_{12}$

$W_e\left(H_1\right)=2\left[2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}{b}_1{b}_2+2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}{b}_3{b}_4+{\displaystyle \underset{i=1}{\overset{n}{\sum }}}{b}_5{b}_6+{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}{b}_7{b}_8\right]+2{\displaystyle \underset{i=1}{\overset{2n-2}{\sum }}}{b}_9{b}_{10}+b_{11}{b}_{12}$

$\begin{array}{l}{W}_{ve}\left(H_1\right)=\frac{1}{2}\{2[2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(a_1{b}_2+a_2{b}_1\right)+2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(a_3{b}_4+a_4{b}_3\right)+{\displaystyle \underset{i=1}{\overset{n}{\sum }}}\left(a_5{b}_6+a_6{b}_5\right)\\ +{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(a_7{b}_8+a_8{b}_7\right)]+2{\displaystyle \underset{i=1}{\overset{2n-2}{\sum }}}\left(a_9{b}_{10}+a_{10}{b}_9\right)+\left(a_{11}{b}_{12}+a_{12}{b}_{11}\right)\}\end{array}$

$\begin{array}{l}S{z}_v\left(H_1\right)=2[2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3i-1\right)a_1{a}_2+2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3i\right)a_3{a}_4+{\displaystyle \underset{i=1}{\overset{n}{\sum }}}\left(3n-1\right)a_5{a}_6\\ +{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3n-2\right)a_7{a}_8]+2{\displaystyle \underset{i=1}{\overset{2n-2}{\sum }}}\left(3i-1\right)a_9{a}_{10}+\left(6n-4\right)a_{11}{a}_{12}\end{array}$

$\begin{array}{l}S{z}_e\left(H_1\right)=2[2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3i-1\right)b_1{b}_2+2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3i\right)b_3{b}_4+{\displaystyle \underset{i=1}{\overset{n}{\sum }}}\left(3n-1\right)b_5{b}_6\\ +{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3n-2\right)b_7{b}_8]+2{\displaystyle \underset{i=1}{\overset{2n-2}{\sum }}}\left(3i-1\right)b_9{b}_{10}+\left(6n-4\right)b_{11}{b}_{12}\end{array}$

$\begin{array}{l}S{z}_{ev}\left(H_1\right)=\frac{1}{2}\{2[2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3i-1\right)\left(a_1{b}_2+a_2{b}_1\right)+2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3i\right)\left(a_3{b}_4+a_4{b}_3\right)\\ +{\displaystyle \underset{i=1}{\overset{n}{\sum }}}\left(3n-1\right)\left(a_5{b}_6+a_6{b}_5\right)+{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3n-2\right)\left(a_7{b}_8+a_8{b}_7\right)\\ +2{\displaystyle \underset{i=1}{\overset{2n-2}{\sum }}}\left(3i-1\right)\left(a_9{b}_{10}+a_{10}{b}_9\right)+\left(6n-4\right)\left(a_{11}{b}_{12}+a_{12}{b}_{11}\right)\}\end{array}$

$S{z}_t\left(H_1\right)=S{z}_v\left(H_1\right)+S{z}_e\left(H_1\right)+2S{z}_{ev}(\; H\; 1\; )$

$\begin{array}{l}PI\left(H_1\right)=2[2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3i-1\right)\left(b_1+b_2\right)+2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3i\right)\left(b_3+b_4\right)+{\displaystyle \underset{i=1}{\overset{n}{\sum }}}\left(3n-1\right)\left(b_5+b_6\right)\\ +{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3n-2\right)\left(b_7+b_8\right)]+2{\displaystyle \underset{i=1}{\overset{2n-2}{\sum }}}\left(3i-1\right)\left(b_9+b_{10}\right)+\left(6n-4\right)\left(b_{11}+b_{12}\right)\end{array}$

$\begin{array}{l}S\left(H_1\right)=2[2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left[a_2\left(2b_1+3i-1\right)+a_1\left(2b_2+3i-1\right)\right]+2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left[a_4\left(2b_3+3i\right)+a_3\left(2b_4+3i\right)\right]\\ +{\displaystyle \underset{i=1}{\overset{n}{\sum }}}\left[a_6\left(2b_5+3n-1\right)+a_5\left(2b_6+3n-1\right)\right]+{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left[a_8\left(2b_7+3n-2\right)+a_7\left(2b_8+3n-2\right)\right]]\\ +2{\displaystyle \underset{i=1}{\overset{2n-2}{\sum }}}\left[a_{10}\left(2b_9+3i-1\right)+a_9\left(2b_{10}+3i-1\right)\right]+\left[a_{12}\left(2b_{11}+6n-4\right)+a_{11}\left(2b_{12}+6n-4\right)\right]\end{array}$

$\begin{array}{l}S\left(H_1\right)=2[2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(2b_1+3i-1\right)\left(2b_2+3i-1\right)+2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(2b_3+3i\right)\left(2b_4+3i\right)\\ +{\displaystyle \underset{i=1}{\overset{n}{\sum }}}\left(2b_5+3n-1\right)\left(2b_6+3n-1\right)+{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(2b_7+3n-2\right)\left(2b_8+3n-2\right)]\\ +2{\displaystyle \underset{i=1}{\overset{2n-2}{\sum }}}\left(2b_9+3i-1\right)\left(2b_{10}+3i-1\right)+\left(2b_{11}+6n-4\right)\left(2b_{12}+6n-4\right)\end{array}$

$\begin{array}{l}Mo\left(H_1\right)=2[2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3i-1\right)\left(a_2-a_1\right)+2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3i\right)\left(a_4-a_3\right)\begin{array}{c}\\ \\ \end{array}\\ +{\displaystyle \underset{i=1}{\overset{\lfloor \frac{n}{2}\rfloor }{\sum }}}\left(3n-1\right)\left(a_6-a_5\right)+{\displaystyle \underset{i=\lfloor \frac{n}{2}\rfloor +1}{\overset{n}{\sum }}}\left(3n-1\right)\left(a_5-a_6\right)\\ +{\displaystyle \underset{i=1}{\overset{\lfloor \frac{n-1}{2}\rfloor }{\sum }}}\left(3n-2\right)\left(a_8-a_7\right)+{\displaystyle \underset{i=\lfloor \frac{n-1}{2}\rfloor +1}{\overset{n-1}{\sum }}}\left(3n-2\right)\left(a_7-a_8\right)]\\ +2{\displaystyle \underset{i=1}{\overset{2n-2}{\sum }}}\left(3i-1\right)\left(a_{10}-a_9\right)+\left(6n-4\right)\left(a_{12}-a_{11}\right)\end{array}$

$\begin{array}{l}Mo\left(H_1\right)=2[2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3i-1\right)\left(b_2-b_1\right)+2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3i\right)\left(b_4-b_3\right)\begin{array}{c}\\ \\ \end{array}\\ +{\displaystyle \underset{i=1}{\overset{\lfloor \frac{n}{2}\rfloor }{\sum }}}\left(3n-1\right)\left(b_6-b_5\right)+{\displaystyle \underset{i=\lfloor \frac{n}{2}\rfloor +1}{\overset{n}{\sum }}}\left(3n-1\right)\left(b_5-b_6\right)\\ +{\displaystyle \underset{i=1}{\overset{\lfloor \frac{n-1}{2}\rfloor }{\sum }}}\left(3n-2\right)\left(b_8-b_7\right)+{\displaystyle \underset{i=\lfloor \frac{n-1}{2}\rfloor +1}{\overset{n-1}{\sum }}}\left(3n-2\right)\left(b_7-b_8\right)]\\ +2{\displaystyle \underset{i=1}{\overset{2n-2}{\sum }}}\left(3i-1\right)\left(b_{10}-b_9\right)+\left(6n-4\right)\left(b_{12}-b_{11}\right)\end{array}$

$\begin{array}{l}Mo\left(H_1\right)=2[2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3i-1\right)\left(a_2+b_2-a_1-b_1\right)+2{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}}\left(3i\right)\left(a_4+b_4-a_3-b_3\right)\begin{array}{c}\\ \\ \end{array}\\ +{\displaystyle \underset{i=1}{\overset{\lfloor \frac{n}{2}\rfloor }{\sum }}}\left(3n-1\right)\left(a_6+b_6-a_5-b_5\right)+{\displaystyle \underset{i=\lfloor \frac{n}{2}\rfloor +1}{\overset{n}{\sum }}}\left(3n-1\right)\left(a_5+b_5-a_6-b_6\right)\\ +{\displaystyle \underset{i=1}{\overset{\lfloor \frac{n-1}{2}\rfloor }{\sum }}}\left(3n-2\right)\left(a_8+b_8-a_7-b_7\right)+{\displaystyle \underset{i=\lfloor \frac{n-1}{2}\rfloor +1}{\overset{n-1}{\sum }}}\left(3n-2\right)\left(a_7+b_7-a_8-b_8\right)]\\ +2{\displaystyle \underset{i=1}{\overset{2n-2}{\sum }}}\left(3i-1\right)\left(a_{10}+b_{10}-a_9-b_9\right)+\left(6n-4\right)\left(a_{12}+b_{12}-a_{11}-b_{11}\right)\end{array}$

把表2中的各项值代入上述相应的表达式中，通过计算简化之后即完成了证明。

4. 结论

多环芳香烃化合物对有机场效应晶体管、发光二极管和太阳能电池板的潜在半导体材料有着广泛的应用。我们认为，这里得到的拓扑指标与多环芳香烃PBAHs(n)的沸点等物理化学性质和一些结构性质的关系有很好的相关性。因此，本文的工作将有助于减少与上述参数有关的实验室工作，并对污染控制和减少大自然空气污染方面有一定的理论指导。同时也希望本研究工作对一些未合成的多环芳香烃起到一定的辅助作用。

基金项目

2021年新疆自治区自然科学基金联合项目(2021D01C078)；国家自然科学基金项目(No.12361072)；2023年新疆维吾尔自治区自然科学基金面上项目(2023D01A36)和青年项目(2023D01B48)；2022年新疆师范大学创新教学团队项目。

NOTES

^*第一作者。

^#通讯作者。