1. 引言
港口是位于江、海、河、湖沿岸,供来往船只停靠、装卸货物和上下旅客的地方,是水陆交通的结点,也是国际间贸易往来的门户。随着港口服务功能的逐渐完善,港口产业链的不断延伸,港口对区域经济的带动作用使得其重要性得到凸显,港口已不再仅仅是联结水路运输、铁路运输与公路运输的枢纽,更是资金、技术、信息的中转站,在国家发展全局中处于战略核心地位。
在港口逐渐成为国家战略性资源,国际与国内港口之间的竞争愈演愈烈的今天,通过研究港口竞争力,并对港口的港口竞争力做出评价,有助于港口找到自身发展中存在的缺陷与不足,突破发展瓶颈,从而在竞争中占据更多优势 [1] 。
2. 理论介绍
2.1. 主成分分析法
假设研究的数据集有P个指标,记为P维随机变量
,该变量的协方差矩阵记为
。主成分分析就是通过线性变换,将原始的P维随机变量X转变为新的P维随机变量Y,
(1)
(2)
其中
为正交矩阵。
主成分分析的中心思想是让数据集的维度减少,但其中的信息要尽可能多地保留。信息可以通过方差来衡量,方差越大,信息就越多。
(3)
第一主成分为
,使其方差最大化就是求解下面这个优化问题:
(4)
设
,两边同时对
求偏导:
(5)
即:
(6)
由此可知
为
的一个特征值,
为这个特征值对应的特征向量。
上式两边左乘
,得:
(7)
因此,
(8)
所以
为
的最大特征值,
为对应的特征向量。
使第二主成分
的方差最大化:
(9)
设
,两边同时对
求偏导,得:
(10)
(10)式两边左乘
,化简得:
,
(11)
(10)式两边左乘
,得:
(12)
而
,因此上式又可以写成:
(13)
得出
。把
代回上式,得:
(14)
由以上可知
为
的第二大特征值,
为对应的特征向量。
以此类推,可得第三个,第四个乃至第P个主成分,这些主成分之间线性无关,因为
(15)
在这P个主成分中选取前r个主成分代替原来P个指标,就实现了主成分方法的降维,其中
的特征值反映了X的信息量。
2.2. 聚类分析法
聚类一般可以分为对样本的聚类和对变量的聚类。在聚类之前,首先需要度量样本之间的距离和类间距离,常用的度量样本之间距离的方法有三种,假设有n个样本和p个变量:
欧式距离:
(16)
绝对距离:
(17)
马氏距离:
(18)
其中,S是由
得到的协方差矩阵
。
常用的度量类间距离的方法有四种:
最短距离法:
(19)
它的直观意义为两个类中最近两点距离。
最长距离法:
(20)
它的直观意义为两个类中最远两点间的距离。
重心法:
(21)
式中:
分别为
的重心。
类平均法:
(22)
它等于
中两样本点距离的平均,
分别为
中的样本点个数。
主要的聚类方法有两种,分别是K-means和层次聚类。
K-means:假设要将n个样本分成k类,先在这n个样本中随机选取k个样本作为起始的聚类中心 [2] ,计算其余样本与这k个聚类中心的欧氏距离,将样本归于距离最小的那一类,然后重新计算聚类中心以及样本点与新的聚类中心的距离并再次进行归类……当聚类中心的位置不再变化时,迭代停止,此时的聚类结果就是最终的结果。
层次聚类:开始时每个样本自成一类,然后每次将类间距离最近的两类合并,合并后重新计算新类与其他类之间的距离,然后再合并……直到所有的样本都被覆盖,最终形成一棵有层次的聚类树。
3. 实证分析
本章主要利用主成分分析和聚类分析的相关理论,对2019年我国年吞吐量在1000万吨以上的13个沿海港口的港口综合竞争力进行分析和评价 [3] ,港口综合竞争力的指标体系如表1所示,数据主要来源于各地区统计年鉴和国家统计局的最新数据。

Table 1. Port comprehensive competitiveness evaluation index system
表1. 港口综合竞争力评价指标体系
3.1. 港口综合竞争力主成分分析
首先对数据进行标准化 [4] 处理,公式如下:
(23)
其中,
表示第i个港口第j个指标的原始取值,
表示标准化后第i个港口第j个指标的数值,
表示第j个指标的平均值,计算公式如下:
(24)
表示第j个指标的标准差:
(25)
计算标准化后数据的相关系数矩阵R:
(26)
将相关系数矩阵可视化,如图1所示。下三角中第i行第j列的数字表示第i个指标和第j个指标的相关系数,相关系数越大,两者的相关性越强,对应上三角中第j行第i列格子圆点的颜色就越深。由图1可知,这13个指标之间相关性较强。
计算相关系数矩阵的特征值和特征向量:
(27)
得出的特征值按从大到小的顺序排列,依次为
,
,
,……,
。根据对应的特征向量
,构造主成分的表达式:
(28)
式中:
,F1为第1主成分,F2为第2主成分,……,F13为第13主成分。
此时还没有实现降维,我们需要从13个主成分中选取前
个主成分作为新的综合性变量,前r个主成分的方差贡献率之和为累积方差贡献率 [5] ,要求大于等于85%。第i个主成分的方差贡献率为
,前r个主成分的累积方差贡献率为
。

Table 2. Variance contribution rate of principal component and cumulative variance contribution rate
表2. 主成分的方差贡献率和累积方差贡献率
由表2可知,当选取三个主成分时,方差的累积贡献率已经超过了80%,当选取六个主成分时,方差的累积贡献率达到了98%,再结合碎石图来决定主成分的个数。
从图2中我们可以很清晰地看到,转折点出现在第2个因子的位置,当主成分的个数大于3时,对应公共因子的特征值小于1,其影响已经很微弱了,因此选取3个主成分较为合适,得到的3个主成分分别是
将标准化后的港口数据带入主成分的表达式,可得各港口前3个主成分的得分,如表3所示,其中C1、C2、C3分别表示第一、第二、第三主成分得分。

Table 3. Port principal component score
表3. 港口主成分得分情况
以三个主成分对应的特征值占比为权,最终得出的主成分得分加权就是各港口的综合得分。主成分得分的权重如表4所示:

Table 4. The weight of the principal component score
表4. 主成分得分的权重
港口综合得分的计算公式如下:
(29)
其中,C为综合得分,C1为第一主成分的得分 [6] ,C2为第二主成分的得分,C3为第三主成分的得分。十三个港口的综合得分及排名如表5所示:

Table 5. Overall score and ranking of ports
表5. 港口的综合得分及排名
在根据主成分分析得出的13个沿海港口综合竞争力的排名中,上海港位列第一,宁波——舟山港则屈居第二,而真实的排名两者却正好相反。宁波——舟山港的货物吞吐量长年占据国内榜首,远远大于上海港,但上海港所在地上海市经济实力雄厚,交通发达,贸易往来频繁,这对于上海港的发展是极其有利的,也使得上海港即便在某些方面不如宁波——舟山港,但预测的排名仍然在宁波——舟山港之上。
天津港和大连港的预测排名和真实排名一致,但青岛港和广州港的排名两者正好调换了位置。无论从货物吞吐量、泊位数量、国民生产总值还是外贸进出口总额,广州港都力压青岛港,但青岛港的实际利用外资额、外贸进出口总额增长率、实际利用外资额都远远大于广州港,2019年广州港的外贸进出口总额增长率为−2.4%,而青岛港的外贸进出口总额增长率为11.4%,这些都进一步说明了青岛港这几年发展的势头要明显强于广州港,发展潜力巨大,因此青岛港的预测排名要优于实际排名。
总体来说,根据主成分分析得出的港口综合竞争力排名与真实排名相差不大,误差在前后一名到两名内浮动,结果的可信度较高。
3.2. 港口综合竞争力聚类分析
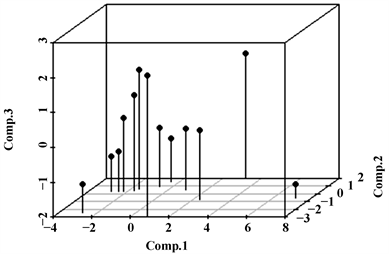
Figure 3. Three-dimensional diagram of port principal component score
图3. 港口主成分得分的三维立体图
图3反映了这13个港口主成分的得分情况。在已经对变量进行主成分降维的前提下,我们对这13个港口进行聚类。
3.2.1. 层次聚类
层次聚类不需要预先确定聚类个数,但需要确定在一个聚类分析中类的最佳数目。一个好的聚类结果,其组内方差必须尽可能的小,而组间方差需要尽可能的大。R语言的NbClust包能够帮助我们确定一个聚类分析中类的最佳数目,结果如表6所示:

Table 6. The selection of the number of hierarchical clustering clusters
表6. 层次聚类聚类数目的选择
聚类个数为2、3和11时,赞同数较多。由于我们的样本港口数只有13,因此聚类个数为2或3比较适宜。
当聚类个数为2时,结果如图4所示:
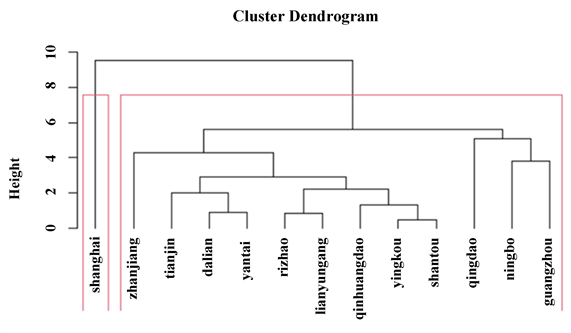
Figure 4. The cluster graph when the number of clusters is 2
图4. 聚类个数为2时的聚类图
当聚类个数为3时,结果如图5所示:
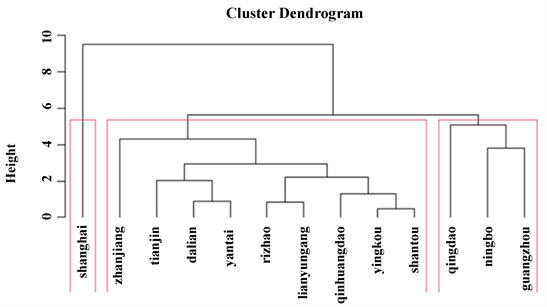
Figure 5. The cluster graph when the number of clusters is 3
图5. 聚类个数为3时的聚类图
3.2.2. 均值聚类
均值聚类需要事先确定所要提取的聚类个数,我们同样可以调用NbClust包来帮助我们确定类的数目,结果如图6所示,其中聚类个数为2和3时,赞同数较多。
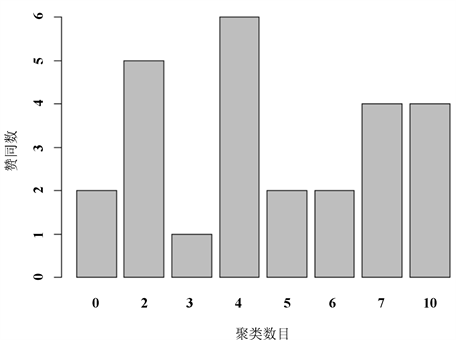
Figure 6. K-means the selection of the number of clusters
图6. K-means聚类数目的选择
也可以参考聚类个数与类内平方、类间平方和的关系曲线图,观察图中曲线的走势变化选择适当的聚类数量。
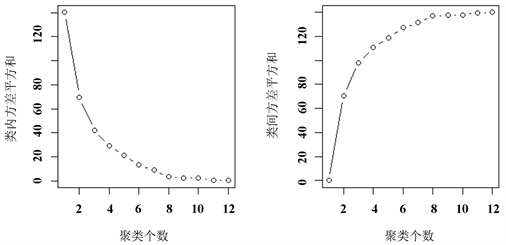
Figure 7. Graph of the relationship between the number of clusters and the squares within and between classes
图7. 聚类个数与类内平方、类间平方的关系曲线图
图7中左表示随着聚类个数的增加,组内方差平方和有一个明显的下降趋势,但在三类之后,下降的趋势减弱。同样地随着聚类个数的增加,组间方差平方和也随之上升,但在三类之后上升的趋势减缓。结合调用NbClust包后所得结果,我们选择2、3、4为聚类的个数。
当聚类个数为2时,结果如表7所示:

Table 7. The result of port clustering when cluster is type 2
表7. 聚为2类时的港口聚类结果
当聚类个数为3时,结果如表8所示:

Table 8. The result of port clustering when cluster is type 3
表8. 聚为3类时的港口聚类结果
当聚类个数为4时,结果如表9所示:

Table 9. The result of port clustering when cluster is type 4
表9. 聚为4类时的港口聚类结果
在聚类分析中,层次聚类的结果和均值聚类的结果截然不同。当把13个港口分成两类时,层次聚类把上海港归为一类,而其他12个港口归为一类;均值聚类则把天津港、上海港、宁波舟山港、青岛港和广州港归为一类,观察可知,这五个港口就是主成分分析中综合得分排名前五的港口。虽然上海港在港口发展规模、港口基础设施建设方面一直处于比上不足,比下有余的状态,但上海港的GDP、第三产业总产值、外贸进出口总额和其他港口相比简直是一骑绝尘,所以说上海港是“全能发展型选手”,把它另归为一类也无可厚非。当把13个港口分为三类时,层次聚类和均值聚类的结果非常相似,只是层次聚类将天津港从宁波舟山港、青岛港和广州港中踢了出去。天津港和青岛港在其他指标上差别不大,但青岛港的实际利用外资额、外贸进出口总额增长率远远大于天津港,所以投资对于港口发展来说是至关重要的。
4. 结论
本文对我国年吞吐量在1000万吨以上的13个沿海港口的港口竞争力进行了分析和评价,得到的排名从前往后依次为:上海港、宁波——舟山港、广州港、天津港、青岛港、大连港、烟台港、日照港、连云港港、秦皇岛港、营口港、汕头港和湛江港。这个预测的排名和真实的排名相差不大,误差在三名以内,说明这种运用主成分分析法对港口进行排名的方法结果可信度较高。
由各港口主成分的得分,我们进行层次聚类和K均值聚类。层次聚类和K均值聚类的结果在聚成两类时相差较大,但在聚成三类时则比较相似。