基于双向期权的多级供应链应急物资储备研究

Multi-Level Supply Chain Emergency Reverse Based on Bidirectional Option Contract

摘要: 针对政企联合储备应急物资研究中，需求不确定和残值问题造成较高的成本风险和物资浪费问题，提出基于双向期权契约的多级供应链应急储备模型。首先基于政企联合储备引入双向期权契约降低物资需求模糊和政府储备的保质期风险，增加代储企业合作机制缓解企业代储和处理物资的压力，以政府成本最小化和企业利润最大化为目标函数构建多级应急物资储备模型。之后对政企合作下实现采供数量、利润协调的期权执行补贴等参数进行可行范围约束，得到多级供应链下协调各方成本/利润的柔性机制。最终进行模拟与仿真发现，在一定条件下该模型降低了政府和企业的储备压力，提高了社会协同参与储备的保障水平，为建立多方协同的应急储备体系提供了相关的理论依据。

Abstract: In current research on government-enterprise joint reserve, fuzzy material demand and residual value result in high-cost risk and material waste, so a multi-level supply chain emergency reserve model based on a bidirectional option contract was proposed. Firstly, the bidirectional option con-tract was introduced based on the government-enterprise joint reserve to reduce material demand uncertainty and the shelf-life risk. The cooperation mechanism of agent storage enterprises was in-creased to relieve storage and disposal pressure, and a multi-level emergency material reserve model was constructed by minimizing government costs and maximizing corporate profits. After that, to achieve procurement and supply quantity and profit coordination under the cooperation between government and enterprise, the feasible range of parameters such as option exercise sub-sidy was restricted, a flexible mechanism to coordinate cost/profit of all parties under the mul-ti-level supply chain was obtained. Finally, numerical simulation shows that under certain condi-tions, the model reduces the pressure on government and enterprises to reserve, enhances the guarantee level of social cooperative participation in the reserve, and provides relevant theoretical basis for establishing multi-party cooperative emergency reserve system.

1. 引言

针对政府与代储企业的应急物资储备，需求模糊往往导致物资短缺或者过多的情况，对于较短保质期的物资来说尤为突出，因此政府和企业要进行更高成本的市场采购或者造成不必要的物资浪费 [1] ；再者充足的物资储备下，代储企业往往需要单独承担更高的储备风险或没有足够的能力进行物资储备和处理，所以供应链整体更有效的合作模式可以降低供应链各方的成本风险，提高应急事件后实物物资的供应数量和救援效率 [2] 。

目前，激励补贴 [3] [4] 、(价格/数量) [5] [6] 柔性契约、期权契约 [7] 是常见的政府与代储企业之间的合作方式。Zhang等 [3] 提出政府对代储企业给与相应的补贴激励来鼓励其进行应急储备的投资，通过建模分析得出政府付出一定的激励成本可以提升供应商的储备水平；Nikkhoo等 [5] 面临需求不足的问题，使用数量柔性契约来协调供应链的物资采购，不仅减少了救援组织的损失，而且降低了供应链的储备成本。Liang等 [8] 将期权合同机制引入救济物资供应链中，扈忠权 [9] 设计了一种基于看跌期权契约的应急物资采购储备模型分别解决需求短缺和具有保质期物资的浪费风险。李健等 [10] 设计了基于双向期权契约的应急物资采购储备模型，与批发契约和看涨期结果对比得到双向期权契约既可以降低政府缺货风险又可以降低物资的保质期风险，更好地实现供应链协调。

政企合作储备降低了政府方单独储备的成本风险，也给代储企业带来相应的储备和物资处理压力。面对该问题，企业间的协调合作可以利用各自的优势进行互补，李晟 [11] [12] 在政企“纵向”委托代理关系的基础上，引入代储供应商间的“横向”合作关系，设计了政企联合储备应急物资激励模型，提升了整体的救援效率。现有文献大多基于双层供应链考虑一对一或一对多的物资储备关系，姜旭等 [13] 则提出代储企业和上游生产型企业“纵向”合作，将部分成品储备转换为上游企业的生产能力储备，形成了包含三方的多级供应链模型，缓解了代储企业原材料储备压力，使供应链各方利润得到提升。为了解决物资储备结束后的物资处理问题，减少物资浪费，本文提出代储企业与拥有仓储能力、销售渠道的下游企业合作，提升物资最终价值同时降低代储企业处理剩余物资的压力。

综上所述，本文考虑基于政企双向期权契约降低政府成本和需求模糊的条件下，将政企形成的双层供应链扩展为多级，令处于上下级的企业进行期权共担，建立由政府、代储企业和其下游企业组成的多级供应链的应急物资储备模型，共同保障物资供应，同时供应链结构的改变丰富了以往研究对于剩余物资的处理方式：通过销售渠道处理剩余物资，增加供应链利润。

2. 问题描述

2.1. 问题说明

政府与代储企业签订双向期权契约，该代储企业再与其下游代储企业达成合作协议，共同承担期权物资的储备工作，此时物资分别由政府的自储物资，代储企业、下游企业储备的期权物资三部分组成。政府首先会与代储企业商定权利金、执行价格、初始的购买数量和期权数量。代储企业决定是否与下游企业合作共同储备。政府承诺若发生灾害，政府自储备量不足或过剩时，会购买或退还不超过与代储企业约定的期权数量，并支付相应的期权执行价格。若总储备不足，则进行市场采购。代储企业和下游企业按照商定储备的实物期权数量分配权利金，期权执行价格由代储企业获得，若使用到下游企业的实物期权，代储企业会给予期权执行补贴。政府的看跌期权由下游企业以剩余价格回收并进行终端市场的售卖。下图1为整体三级供应链的应急物资采购流程图。

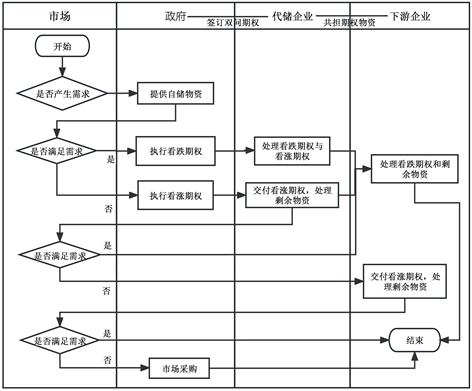
Figure 1. Three-level supply chain emergency supplies procurement flow chart

图1. 三级供应链应急物资采购流程图

2.2. 假设

a) 本文的研究对象为保质期较短且灾后需求量激增的应急物资，暂时不考虑生产能力的储备；

b) 本文所涉及的供应链成员皆为理性、风险中性的，各方均出于利弊权衡后自愿合作，政府不会逼迫代储企业进行灾后紧急物资的供应 [14] ；

c) 本文设定场景为单周期，且周期长度不超过物资的保质期，物资的剩余价值是指物资并未过期前的价值。

2.3. 符号说明

$Q$ ：政府自行储备实物物资数量q：政府购买的期权数量

$q_1$ ：代储企业储备的期权数量 $q_2$ ：下游企业储备期权数量

$w_1$ ：实物采购物资的批发价 $w_2$ ：现货市场购买物资的价格

$c$ ：代储企业生产应急物资的单位生产成本 $v$ ：应急物资的残值

$h$ ：代储企业和政府的单位储存成本， $\rho$ ：灾害发生的概率 $\left(0\le \rho \le 1\right)$

$w_3$ ：下游企业处理物资的售卖价格 $o$ ：双向期权的权利金金额

$e_1$ ：看涨期权的执行价格 $e_2$ ：看跌期权的执行价格

$x$ ：应急事件发生后应急物资的需求量， $F\left(x\right)$ 函数为需求x的概率分布函数， $f\left(x\right)$ 为概率密度函数，最大值为U，均值为 $\mu$

$c_1$ ：代储企业给予下游企业的期权执行补贴

根据文献 [9] [10] 中对于参数的设置，为了使模型更加科学合理，现对以上参数进行约束： $w_2>w_1$ 且 $w_2>o+e_1$ ，否则政府没有理由进行物资的提前储备，为了保证代储企业合理的利益，需满足 $w_1>c+h>v$ ，一般情况下，随着物资保质期的缩短，看涨期权执行价格要大于看跌期权执行价格，所以需保证 $e_1>e_2$ 。

3. 模型

3.1. 双向期权契约模型

灾害发生前，政府以批发价格 $w_1$ 向代储企业采购Q单位的实物物资作为自身储备，以权利金o购买q单位的看涨期权和Q单位的看跌期权，灾害结束根据实际需求以 $e_1$ 和 $e_2$ 分别执行对应数量的看涨、看跌期权；代储企业根据与政府商议的数量进行生产储备。

3.1.1. 政府决策分析

政府的成本函数为：若未发生灾害， $E{C}_{g1}^b=\left(w_1+h+o-e_2\right)Q+oq$ ；

若发生灾害，

$\begin{array}{l}E{C}_{g2}^b=\left(w_1+h+o\right)Q+oq-{\displaystyle {\int }_0^Q{e}_2\left(Q-x\right)}f\left(x\right)\text{d}x+{\displaystyle {\int }_Q^{Q+q}{e}_1\left(x-Q\right)f\left(x\right)\text{d}x}\\ +{\displaystyle {\int }_{Q+q}^U\left[w_2\left(x-Q-q\right)+e_{1}q\right]f\left(x\right)\text{d}x}=w_{2}U+\left(w_1+h+o-w_2\right)Q+\left(o+e_1-w_2\right)q\\ -e_2{\displaystyle {\int }_0^{Q}F\left(x\right)\text{d}x}-e_1{\displaystyle {\int }_Q^{Q+q}F\left(x\right)\text{d}x}-w_2{\displaystyle {\int }_{Q+q}^{U}F\left(x\right)\text{d}x}\end{array}$

综上，政府的期望成本函数为：

$\begin{array}{c}E{C}_g^b=\left(w_1+h+o-e_2\right)Q+oq+\rho w_{2}U+\rho \left(e_2-w_2\right)Q+\rho \left(e_1-w_2\right)q\\ -\rho e_2{\displaystyle {\int }_0^{Q}F\left(x\right)\text{d}x-\rho e_1{\displaystyle {\int }_Q^{Q+q}F\left(x\right)\text{d}x}-\rho w_2{\displaystyle {\int }_{Q+q}^{U}F\left(x\right)\text{d}x}}\end{array}$ (1)

命题1当 $o<\frac{\left(w_1+h-e_2\right)\left(w_2-e_1\right)}{\left(e_1-e_2\right)}$ 且 $e_1>\frac{w_1+h+\left(1-\rho \right)e_2}{\rho }$ 时，双向期权成立，此时政府的最优采购决策为 $Q_g^{b*}=F^{-1}\left[1-\frac{w_1+h-e_2}{\rho \left(e_1-e_2\right)}\right];q_g^{b*}=F^{-1}\left[1-\frac{o}{\rho \left(w_2-e_1\right)}\right]-Q;$

证明分别对政府期望成本函数求关于 $Q、q$ 的一阶、二阶导数，得到：

$\begin{array}{l}\frac{\partial E{C}_e^b}{\partial Q}=\left(w_1+o+h-e_2\right)+\rho \left(e_2-w_2\right)+\rho \left(e_1-e_2\right)F\left(Q\right)+\rho \left(w_2-e_1\right)F\left(Q+q\right);\\ \frac{\partial E{C}_e^b}{\partial q}=o+\rho \left(e_1-w_2\right)+\rho \left(w_2-e_1\right)F\left(Q+q\right);\frac{{\partial }^{2}E{C}_e^b}{\partial Q^2}=\rho \left(w_2-e_1\right)f\left(Q+q\right)+\rho \left(e_1-e_2\right)f\left(Q\right)>0\\ \frac{{\partial }^{2}E{C}_e^b}{\partial q^2}=\rho \left(w_2-e_1\right)f\left(Q+q\right)>0;\frac{{\partial }^{2}E{C}_e^b}{\partial Q\partial q}=\frac{{\partial }^{2}E{C}_e^b}{\partial q\partial Q}=\rho \left(w_2-e_1\right)f\left(Q+q\right)>0\end{array}$

由 $\frac{{\partial }^{2}E{C}_e^b}{\partial Q^2},\frac{{\partial }^{2}E{C}_e^b}{\partial q^2}>0$ ，且 $\left|\begin{array}{cc}\frac{{\partial }^{2}E{C}_e^b}{\partial Q^2}& \frac{{\partial }^{2}E{C}_e^b}{\partial Q\partial q}\\ \frac{{\partial }^{2}E{C}_e^b}{\partial q\partial Q}& \frac{{\partial }^{2}E{C}_e^b}{\partial q^2}\end{array}\right|>0$ ，可知政府期望成本函数相对于自储量和期权购买量来说为凸函数，分别令 $\frac{\partial E{C}_e^b}{\partial Q},\frac{\partial E{C}_e^b}{\partial q}=0$ 联立求解，计算得到 $F\left(Q_g^{b*}\right)=1-\frac{w_1+h-e_2}{\rho \left(e_1-e_2\right)};F\left(Q_g^{b*}+q_g^{b*}\right)=1-\frac{o}{\rho \left(w_2-e_1\right)};$ 若使得双向期权成立，需满足 $0<F\left(Q_g^{b*}\right)<F\left(Q_g^{b*}+q_g^{b*}\right)<1$ ，计算得 $o<\frac{\left(w_1+h-e_2\right)\left(w_2-e_1\right)}{\left(e_1-e_2\right)}$ 且 $e_1>\frac{w_1+h-e_2}{\rho }+e_2$ 。

3.1.2. 代储企业决策分析

利润函数为：若未发生灾害， $E{R}_{e1}^b=\left(w_1+o+v-c-e_2\right)Q+\left(o+v-c-h\right)q$

若发生灾害，

$\begin{array}{c}E{R}_{e2}^b=\left(w_1+o-c\right)Q+\left(o-c-h\right)q+{\displaystyle {\int }_0^Q\left[v\left(Q+q-x\right)-e_2\left(Q-x\right)\right]}f\left(x\right)\text{d}x\\ +{\displaystyle {\int }_Q^{Q+q}\left[e_1\left(x-Q\right)+v\left(Q+q-x\right)\right]f\left(x\right)\text{d}x}+{\displaystyle {\int }_{Q+q}^U{e}_{1}q}f\left(x\right)\text{d}x\\ =\left(w_1+o-c\right)Q+\left(o+e_1-c-h\right)q-e_2{\displaystyle {\int }_0^{Q}F\left(x\right)\text{d}x}-e_1{\displaystyle {\int }_Q^{Q+q}F\left(x\right)\text{d}x}+v{\displaystyle {\int }_0^{Q+q}F\left(x\right)\text{d}x}\end{array}$

综上，代储企业的期望利润函数为

$\begin{array}{c}E{R}_e^b=\left(w_1+o+v-c-e_2\right)Q+\left(o+v-c-h\right)q+\rho \left(e_2-v\right)Q+\rho \left(e_1-v\right)q\\ -\rho e_2{\displaystyle {\int }_0^{Q}F\left(x\right)\text{d}x}-\rho e_1{\displaystyle {\int }_Q^{Q+q}F\left(x\right)\text{d}x+\rho v{\displaystyle {\int }_0^{Q+q}F\left(x\right)\text{d}x}}\end{array}$ (2)

对(3)求解关于 $Q、q$ 的一、二阶导数，得到

$\begin{array}{l}\frac{\partial E{C}_e^b}{\partial Q}=\left(w_1+o+v-c-h\right)+\rho \left(e_2-v\right)+\rho \left(e_1-e_2\right)F\left(Q\right)+\rho \left(v-e_1\right)F\left(Q+q\right);\\ A=\frac{{\partial }^{2}E{C}_e^b}{\partial Q^2}=\rho \left(e_1-e_2\right)f\left(Q\right)+\rho \left(v-e_1\right)f\left(Q+q\right);\\ \frac{\partial E{C}_e^b}{\partial q}=\left(o+v-c-h\right)+\rho \left(e_1-v\right)+\rho \left(v-e_1\right)F\left(Q+q\right);B=\frac{{\partial }^{2}E{C}_e^b}{\partial q^2}=\rho \left(v-e_1\right)f\left(Q+q\right)<0\\ C=\frac{{\partial }^{2}E{C}_e^b}{\partial Q\partial q}=\frac{{\partial }^{2}E{C}_e^b}{\partial q\partial Q}=\rho \left(v-e_1\right)f\left(Q+q\right);\left|\begin{array}{cc}\frac{{\partial }^{2}E{C}_e^b}{\partial Q^2}& \frac{{\partial }^{2}E{C}_e^b}{\partial Q\partial q}\\ \frac{{\partial }^{2}E{C}_e^b}{\partial q\partial Q}& \frac{{\partial }^{2}E{C}_e^b}{\partial q^2}\end{array}\right|=A\text{·}B-C^2<0\end{array}$

由结果可知双向期权下存在最优储备决策使得代储企业期望利润函数有最大值，计算得 $F\left(Q_e^{b*}\right)=1-\frac{w_1+h-e_2}{\rho \left(e_1-e_2\right)};F\left(Q_e^{b*}+q_e^b{}^{*}\right)=1-\frac{c+h-o-v}{\rho \left(e_1-v\right)};$ 由此可知代储企业最优期权储备量为 $q_e^{b*}=F^{-1}\left[1-\frac{c+h-o-v}{\rho \left(e_1-v\right)}\right]-Q$ 。

3.1.3. 双向期权契约下的供应链协调

综合以上分析，在政府与代储企业签订双向期权契约下整体供应链的期望利润函数为

$\begin{array}{c}E{R}_c^b=\left(v-c-h\right)\left(Q+q\right)+\rho w_{2}Q+\rho \left(w_2-v\right)\left(Q+q\right)\\ +\rho v{\displaystyle {\int }_0^{Q+q}F\left(x\right)\text{d}x}+\rho w_2{\displaystyle {\int }_{Q+q}^{U}F\left(x\right)\text{d}x}\end{array}$ (3)

根据供应链协调的定义，有 $E{R}_c^b=E{R}_e^b-E{R}_g^b$ ，通过(1)~(3)式计算得到 $Q_c^{b*}=Q_g^{b*}+q_e^{b*}$ ，即 $\frac{o}{\rho \left(w_2-e_1\right)}=\frac{c+h-o-v}{\rho \left(e_1-v\right)}=\frac{c+h-v}{\rho \left(w_2-v\right)}$ ，计算得 $o=\frac{\left(c+h-v\right)\left(w_2-e_1\right)}{w_2-v}$ ，此时供应链达到协调，供应链双方都将实现最优决策。

3.2. 政企双向期权下代储与下游合作企业签订共储期权模型

3.2.1. 代储企业期望利润

代储企业的利润函数为：

若未发生灾害， $E{R}_{e11}^t=\left(w_1+o+v-c-e_2\right)Q+\left(o+v-c-h\right)q_1+\left(w_1-c\right)q_2$

若发生灾害，

$\begin{array}{l}E{R}_{e12}^t=\left(w_1+o-c\right)Q+\left(o-c-h\right)q_1+\left(w_1-c\right)q_2+{\displaystyle {\int }_0^Q\left[v{q}_1+\left(v-e_2\right)\left(Q-x\right)\right]f\left(x\right)\text{d}x}\\ +{\displaystyle {\int }_Q^{Q+q_1}\left[e_1\left(x-Q\right)+v\left(Q+q_1-x\right)\right]f\left(x\right)\text{d}x}+{\displaystyle {\int }_{Q+q_1}^{Q+q_1+q_2}{e}_1{q}_1}+\left(e_1-c_1\right)\left(x-Q-q_1\right)f\left(x\right)\text{d}x\\ +{\displaystyle {\int }_{Q+q_1+q_2}^U\left[e_1\left(q_1+q_2\right)-c_1{q}_2\right]f\left(x\right)\text{d}x}=\left(w_1+o-c\right)Q+\left(e_1+o-c-h\right)q_1+\left(e_1+w_1-c_1-c\right)q_2\\ -e_2{\displaystyle {\int }_0^{Q}F\left(x\right)\text{d}x}+v{\displaystyle {\int }_0^{Q+q_1}F\left(x\right)\text{d}x}-e_1{\displaystyle {\int }_Q^{Q+q_1+q_2}F\left(x\right)\text{d}x}+c_1{\displaystyle {\int }_{Q+q_1}^{Q+q_1+q_2}F\left(x\right)\text{d}x}\end{array}$

综上所述，代储企业的期望利润函数为

$\begin{array}{c}E{R}_{e1}^t=\left(w_1+o+v-c-e_2\right)Q+\left(o+v-c-h\right)q_1+\left(w_1-c\right)q_2\\ +\rho \left(e_2-v\right)Q+\rho \left(e_1-v\right)q_1+\rho \left(e_1-c_1\right)q_2-\rho e_2{\displaystyle {\int }_0^{Q}F\left(x\right)\text{d}x}\\ -\rho e_1{\displaystyle {\int }_Q^{Q+q_1+q_2}F\left(x\right)\text{d}x}+\rho v{\displaystyle {\int }_0^{Q+q_1}F\left(x\right)\text{d}x}+\rho c_1{\displaystyle {\int }_{Q+q_1}^{Q+q_1+q_2}F\left(x\right)\text{d}x}\end{array}$ (4)

对(4)式求解关于 $q_1,q_2$ 的一、二阶导数，得

$\begin{array}{l}\frac{\partial E{R}_{e1}^t}{\partial q_1}=o+v-c-h+\rho \left(e_1-v\right)+\rho \left(v-c_1\right)F\left(Q+q_1\right)+\rho \left(c_1-e_1\right)F\left(Q+q_1+q_2\right);\\ \frac{{\partial }^{2}E{R}_{e1}^t}{\partial q_1{}^2}=\rho \left(v-c_1\right)f\left(Q+q_1\right)+\rho \left(c_1-e_1\right)f\left(Q+q_1+q_2\right);\\ \frac{\partial E{R}_{e1}^t}{\partial q_2}=\left(w_1-c\right)+\rho \left(e_1-c_1\right)+\rho \left(c_1-e_1\right)F\left(Q+q_1+q_2\right);\\ \frac{{\partial }^{2}E{R}_{e1}^t}{\partial q_2{}^2}=\rho \left(c_1-e_1\right)f\left(Q+q_1+q_2\right);\frac{{\partial }^{2}E{R}_{e1}^t}{\partial q_1{q}_2}=\frac{{\partial }^{2}E{R}_{e1}^t}{\partial q_2{q}_1}=\rho \left(c_1-e_1\right)f\left(Q+q_1+q_2\right);\end{array}$

因为 $\left|\begin{array}{cc}\frac{{\partial }^{2}E{R}_{e1}^t}{\partial q_1{}^2}& \frac{{\partial }^{2}E{R}_{e1}^t}{\partial q_1{q}_2}\\ \frac{{\partial }^{2}E{R}_{e1}^t}{\partial q_2{q}_1}& \frac{{\partial }^{2}E{R}_{e1}^t}{\partial q_2{}^2}\end{array}\right|<0$ ，由此可知代储企业期望利润有最优决策，令 $\frac{\partial E{R}_{e1}^t}{\partial q_1},\frac{\partial E{R}_{e1}^t}{\partial q_2}=0$ ，得 $q_{e1}^{t*}=F^{-1}\left[1-\frac{w_1+h-o-v}{\rho \left(c_1-v\right)}\right]-Q;q_{e2}^{t*}=F^{-1}\left[1-\frac{w_1-c}{\rho \left(c_1-e_1\right)}\right]-Q-q_1$ 。

3.2.2. 合作企业期望利润

利润函数为：若未发生灾害， $E{R}_{e21}^t=\left(w_3+o-h-w_1\right)q_2+\left(w_3-v\right)Q$

若发生灾害，

$\begin{array}{c}E{R}_{e22}^t=\left(o-h-w_1\right)q_2+{\displaystyle {\int }_0^Q\left(w_3-v\right)\left(Q-x\right)}f\left(x\right)\text{d}x+{\displaystyle {\int }_0^{Q+q_1}{w}_3{q}_2}f\left(x\right)\text{d}x\\ +{\displaystyle {\int }_{Q+q_1}^{Q+q_1+q_2}\left[c_1\left(x-Q-q_1\right)+w_3\left(Q+q_1+q_2-x\right)\right]f\left(x\right)\text{d}x}+{\displaystyle {\int }_{Q+q_1+q_2}^U{c}_1{q}_{2}f\left(x\right)\text{d}x}\\ =\left(o+c_1-h-w_1\right)q_2+\left(w_3-v\right){\displaystyle {\int }_0^{Q}F\left(x\right)\text{d}x}+\left(w_3-c_1\right){\displaystyle {\int }_{Q+q_1}^{Q+q_1+q_2}F\left(x\right)\text{d}x}\end{array}$

综上，下游合作企业的利润函数为，

$\begin{array}{c}E{R}_{e2}^t=\left(w_3+o-h-w_1\right)q_2+\left(1-\rho \right)\left(w_3-v\right)Q+\rho \left(c_1-w_3\right)q_2\\ +\rho \left(w_3-v\right){\displaystyle {\int }_0^{Q}F\left(x\right)\text{d}x}+\rho \left(w_3-c_1\right){\displaystyle {\int }_{Q+q_1}^{Q+q_1+q_2}F\left(x\right)\text{d}x}\end{array}$ (5)

命题2双向期权成立的情况下，当政府设置的权利金o与代储企业给与的期权执行补贴满足 $h+w_1-w_3-\rho \left(c_1-w_3\right)\le o\le h+w_1-w_3$ 时，存在下游企业愿意为其进行代储和剩余物资的处理，代储企业与下游企业最优储备决策如下：

a) 当 $h+w_1-w_3-\rho \left(c_1-w_3\right)\le o\le h+w_1-w_3$ 存在，下游企业愿意与代储企业共同储备期权物资，双方整体供应链利润函数相对于 $q_1$ 和 $q_2$ 为凹函数，此时双方的最优储备数量为集中决策下的最优决策：

$q_1^{*}=F^{-1}\left[1-\frac{w_1+h-o-v}{\rho \left(c_1-v\right)}\right]-Q;q_2^{*}=F^{-1}\left[\frac{w_3+o-h-w_1}{\rho \left(c_1-w_3\right)}+1\right]-Q-q_1$

b) 当 $o<h+w_1-w_3-\rho \left(c_1-w_3\right)$ 或者 $o>h+w_1-w_3$ 时，出于供应链中各方利润考虑不会发生与下游企业的合作，此时代储企业储备所有的期权物资，储备总量为 $q_e^{b*}=F^{-1}\left[\frac{o+v-h-c}{\rho \left(e_1-v\right)}+1\right]-Q$ 。

证明如下：对下游合作企业期望利润函数(6)中 $q_2$ 求一、二阶导数，分别为：

$\begin{array}{l}\frac{\partial E{R}_{e2}^t}{\partial q_2}=w_3+o-h-w_1+\rho \left(c_1-w_3\right)\left[1-F\left(Q+q_1+q_2\right)\right];\\ \frac{{\partial }^{2}E{R}_{e2}^t}{\partial q_2{}^2}=\rho \left(w_3-c_1\right)f\left(Q+q_1+q_2\right)<0\end{array}$

所以下游合作企业期望利润函数关于 $q_2$ 的一阶导数单调递减。当 $o<h+w_1-w_3-\rho \left(c_1-w_3\right)$ 时， $\partial E{R}_{e2}^t/\partial q_2<0$ ，此时 $E{R}_{e2}^t$ 相对于 $q_2$ 单调递减，此时合作企业出于自身利益考虑不会与代储企业合作共同储备看涨期权物资；当 $o>h+w_1-w_3$ 时， $\partial E{R}_{e2}^t/\partial q_2>0$ ，此时 $E{R}_{e2}^t$ 相对于 $q_2$ 单调递增，对于下游企业来说储备数量越多利润越大；当 $h+w_1-w_3-\rho \left(c_1-w_3\right)\le o\le h+w_1-w_3$ 时， $E{R}_{e2}^t$ 先递增后递减，令 $\partial E{R}_{e2}^t/\partial q_2=0$ ，则下游企业期望利润函数最大时看涨期权数量为 $q_{e2}^{t**}=F^{-1}\left[\frac{w_3+o-h-w_1}{\rho \left(c_1-w_3\right)}+1\right]-Q-q_1$ 。此时为下游企业参与代储企业合作共同储备看涨期权时最优的储备数量。

3.2.3. 代储企业与下游企业的供应链协调

该模式下代储企业与下游企业共同组成的供应链期望利润为

$\begin{array}{c}E{R}_e^t=\left(w_1+o+w_3-c-e_2\right)Q+\left(o+v-c-h\right)q_1+\left(w_3+o-c-h\right)q_2\\ +\rho \left(e_2-w_3\right)Q+\rho \left(e_1-v\right)q_1+\rho \left(e_1-w_3\right)q_2+\rho \left(w_3-v-e_2\right){\displaystyle {\int }_0^{Q}F\left(x\right)\text{d}x}\\ +\rho v{\displaystyle {\int }_0^{Q+q_1}F\left(x\right)\text{d}x}-\rho e_1{\displaystyle {\int }_Q^{Q+q_1+q_2}F\left(x\right)\text{d}x}+\rho w_3{\displaystyle {\int }_{Q+q_1}^{Q+q_1+q_2}F\left(x\right)\text{d}x}\end{array}$ (6)

对(6)求解关于 $q_1,q_2$ 的一二阶导数，得到

$\begin{array}{l}\frac{\partial E{R}_e^t}{\partial q_1}=\left(o+v-c-h\right)+\rho \left(e_1-v\right)+\rho \left(v-w_3\right)F\left(Q+q_1\right)+\rho \left(w_3-e_1\right)F\left(Q+q_1+q_2\right)\\ A=\frac{{\partial }^{2}E{R}_e^t}{\partial q_1{}^2}=\rho \left(v-w_3\right)f\left(Q+q_1\right)+\rho \left(w_3-e_1\right)f\left(Q+q_1+q_2\right)\\ \frac{\partial E{R}_e^t}{\partial q_2}=\left(w_3+o-h-c\right)+\rho \left(e_1-w_3\right)+\rho \left(w_3-e_1\right)F\left(Q+q_1+q_2\right)\\ B=\frac{{\partial }^{2}E{R}_e^t}{\partial q_2{}^2}=C=\frac{{\partial }^{2}E{R}_e^t}{\partial q_1{q}_2}=\frac{{\partial }^{2}E{R}_e^t}{\partial q_2{q}_1}=\rho \left(w_3-e_1\right)f\left(Q+q_1+q_2\right)\end{array}$

Hessian矩阵 $\left|\begin{array}{cc}\frac{{\partial }^{2}E{R}_e^t}{\partial q_1{}^2}& \frac{{\partial }^{2}E{R}_e^t}{\partial q_1{q}_2}\\ \frac{{\partial }^{2}E{R}_e^t}{\partial q_2{q}_1}& \frac{{\partial }^{2}E{R}_e^t}{\partial q_2{}^2}\end{array}\right|=A\text{·}B-C^2={\rho }^2\left(w_3-e_1\right)\left(v-w_3\right)<0$ ，可知，代储企业与下游合作企业组成的供应链的整体期望利润相对于 $q_1,q_2$ 为凹函数。代储企业存在最优储备期权数量 $q_{1s}^{*}$ 和下游企业最优储备 $q_{2s}^{*}$ 使得双方组成的供应链利润最大。此时双方最优共同储备为 $q_c^{t*}=F^{-1}\left[\frac{w_3+o-h-c}{\rho \left(e_1-w_3\right)}+1\right]-Q$ 。根据供应链协调定义，存在 $E{R}_{e1}^t+E{R}_{e2}^t=E{R}_e^t$ ，此时有 $1+\frac{w_3+o-h-c}{\rho \left(e_1-w_3\right)}=1-\frac{w_1-c}{\rho \left(c_1-e_1\right)}=\frac{w_3+o-h-w_1}{\rho \left(c_1-w_3\right)}+1$ ，计算得到 $c_1=\frac{\left(w_1-c\right)\left(e_1-w_3\right)}{w_3+o-c-h}+e_1$ 。此时供应链达到协调且双方都会得到最优决策。

命题3代储企业给与下游企业相应的期权执行补贴需满足 $c_1<v-\frac{2U\left(o+v-w_1-h\right)}{\rho \left(2U-2Q-2q_1-q_2\right)}$ 来保证代储企业的利益不受到损害，否则代储企业将不会考虑与其他企业进行合作。

证明：假设期权储备总量不变，代储企业与下游企业合作后的期望利润变化为

$\Delta E{R}_e=E{R}_{e2}^t-E{R}_{e1}^t=\left(w_1+h-o-v\right)q_2+\rho \left(v-c_1\right)q_2-\rho \left(v-c_1\right){\displaystyle {\int }_{Q+q_1}^{Q+q_1+q_2}F\left(x\right)\text{d}x}$ ，假设需求数量服从均匀分布，当 $\Delta E{R}_e>0$ 时，代储企业与下游企业合作后的利润变化大于0，此时代储企业会选择与下游企业共同储备期权物资，计算得 $c_1<v-\frac{2U\left(o+v-w_1-h\right)}{\rho \left(2U-2Q-2q_1-q_2\right)}$ 。

由命题2和命题3结果可知，当代储企业和下游企业合作后，假设二者共同储备的期权数量不变，当权利金和代储企业给与下游企业的期权执行补贴满足一定的条件时，代储企业和下游企业的利润变化都大于0，现根据权利金和期权执行补贴进行综合分析得出：当 $h+w_1-w_3-\rho \left(c_1-w_3\right)<o<h+w_1-w_3$ 且 $\Delta E{R}_e>0$ 时，双方都愿意参与合作，且代储企业与下游企业合作后利润变化都大于0，此时双方各自最优储备数量为命题2的情形a。

4. 模拟与仿真

为了验证本文所述模型的有效性，现设置一系列参数：政府与当地一家供应商合作共同储备应急物资，供应商选择与其下游企业共同合作储备期权物资，假设应急物资的需求量服从[0, 20,000] [14] [15] [16] 均匀分布，其中 $U=20000,w_1=30,h=2,e_1=45,e_2=15,c=20,w_2=80,v=10$ 。

4.1. ρ对于各方储备数量的影响

下图2为代储企业与下游企业不合作以及合作时灾害发生概率的变化对于各方储备量的影响：

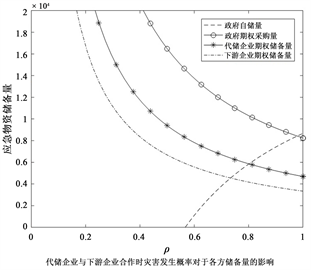(a) (b)

Figure 2. The impact of disaster probability on the reserves in different modes

图2. 灾害发生概率在不同模式下对于各方储备量的影响

由图2中(a)可知，随着灾害发生概率的增大，对于政府来说充分的物资储备可以更好地应对可能发生的自然灾害，所以政府会采购储备更多的物资数量。

结合(a)和(b)，不管代储企业是否与下游企业合作，随着灾害发生概率不断增大，企业会逐渐减少物资储备数量以减少自身所承担的成本风险，而下游企业作为与代储企业共同承担储备期权物资的合作方相对于代储企业来说期权储备数量减少的趋势更大。

4.2. c₁对于应急物资储备量及各方利润的影响

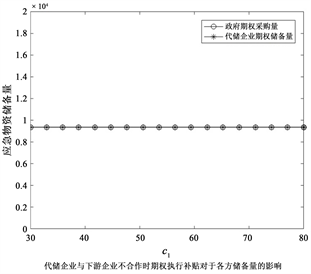
下图3为代储企业与下游企业不合作以及合作时期权执行补贴的变化对于各方储备量的影响。

观察(b)可知因为期权执行补贴是代储企业与下游企业之间的激励补贴，所以政府的期权采购量并不受期权执行补贴的影响，而随着期权执行补贴的增大，代储企业的期权储备量增加，下游企业储备量逐渐减少，这是因为期权补贴的提升增加了代储企业的成本，代储企业会相应地减少由下游企业储备的物资转而自行储备。由两张图对比可知适当的调节期权执行补贴可以使得企业双方共同储备的物资数量大于企业单独储备期权时的数量。

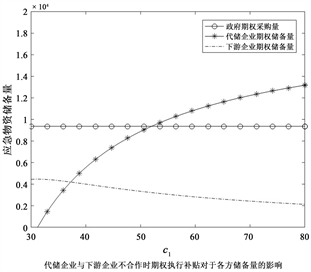(a) (b)

Figure 3. The impact of Option exercise subsidy on the reserves in different modes

图3. 期权执行补贴在不同模式下对于各方储备量的影响

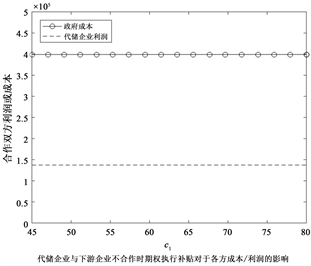
下图4为期权执行补贴的变化对于供应链各方成本或者利润的影响：

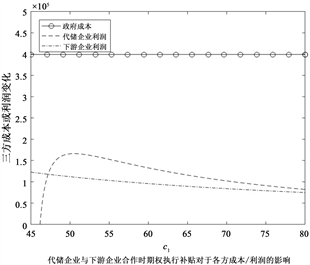(a) (b)

Figure 4. The impact of Option exercise subsidy on the Government costs and enterprise profits in different modes

图4. 期权执行补贴在不同模式下对于各方成本/利润的影响

观察(a)、(b)可知，在代储企业与下游企业合作后，合适的期权执行补贴价格可以满足不损害代储企业利润的情况下使得下游企业获得利润；同时由图3和图4可知政府的最优采购量和最优自储量并不受期权执行补贴的影响，所以政府的期望成本不会随着双方企业合作的期权执行补贴的变动而发生改变。

4.3. o对于应急物资储备量及利润影响

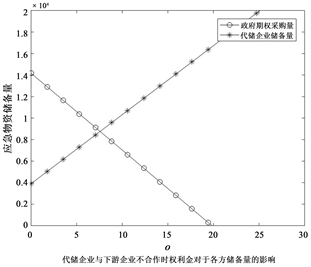
下图5为代储企业与下游企业不合作以及合作时权利金的变化对于供应链各方储备量的影响：

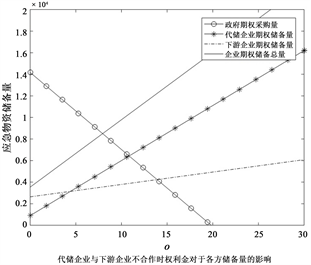(a) (b)

Figure 5. The impact of Option price on the reserves in different modes

图5. 权利金在不同模式下对于各方储备量的影响

因为权利金的提高会增加政府储备物资的总成本和企业储备期权物资的总利润，由(a) (b)对比可知，政府期权的采购量会随着权利金金额的增加逐渐减少，代储企业和下游企业总的储备数量并没有明显变化，但是代储企业的物资数量因为下游企业的合作而降低。

结合表1分析，当政府方采购数量与企业方储备数量相同时，加入下游企业后的权利金降低，此时政府的最优采购量并没有因为双方的合作有大幅度的增加，所以本文提出的模式可以保证在相同的灾害发生概率的情况下，下游企业的加入不会导致过多采购物资，造成过多的浪费，相反可以通过下游企业的销售渠道最终出售剩余物资，增加剩余物资的价值。

Table 1. Comparison of the results of two modes after achieving coordination

表1. 双层供应链与多级供应链达到协调之后的结果对比

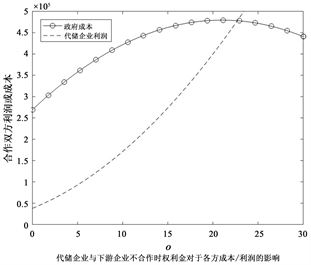
下图6为供应链各方成本/利润随着权利金不断增加的变化曲线。

对比(a)和(b)，不管下游企业是否加入双层供应链，政府成本和企业利润与权利金始终呈正比；对比两图的代储企业利润曲线，在权利金满足一定条件时，代储企业的利润会大于其单独储备期权物资时的利润；另外，政府的成本在权利金超过一定数值后，(图中在o大于20后)，成本开始呈下降趋势，本文分析因为权利金过高导致政府的合作意愿下降，不再进行期权物资的采购代储。

(a) (b)

Figure 6. The impact of Option price on the Government costs and enterprise profits in different modes

图6. 权利金在不同模式下对于各方成本/利润的影响

结合表1可知，加入下游企业后权利金降低，政府的成本随之降低，代储企业因为与下游合作其利润没有受到损害。

5. 总结

本文提出在双层应急供应链中加入下游企业形成多级供应链，并通过数值实验研究灾害发生概率、权利金以及期权执行补贴对于三方最优的物资储备数量以及成本/利润的影响，验证本文提出的合作模式和模型的有效性。

通过数值仿真将本文多级供应链模型与双层供应链模型的最优决策对比，可以得出本文提出的模型可以在降低政府成本、不降低代储企业利润的情况下，很好地分担代储企业的储备风险，增加一定的最优储备数量，不造成过多的物资浪费，同时给下游企业带来一定的利润。

需要注意的是，对于发生概率更大的应急事件，企业的储备数量相对减少，此时政府可以通过提高权利金和看涨期权执行价格来提升总体的储备数量，代储企业参与合作后可行的期权执行补贴范围较小，所以代储企业需谨慎评估合作风险。

本文所假设的情况是下游企业可以借助政府影响力和公信力将剩余物资以不低于批发价出售给消费者，这是本文所存在的问题，并没有去讨论剩余物资的实际销量与剩余保质期的关系，这也是今后值得研究的一个方向。

基金项目

国家社会科学基金项目(22BGL240)。

NOTES

^*第一作者。

^#通讯作者。