基于LSTM模型的草原土壤状态预测

Grassland Soil Condition Prediction Based on LSTM Model

摘要: 中国是一个资源大国，拥有丰富的草地。这些草原生态系统是保持我国生态平衡的关键防线，同时为经济发展提供稳固的基础。然而，随着畜牧业的迅速发展，草地退化问题日益突出，甚至在一些地区呈现沙漠化趋势。面对这一情况，迫切需要提供科学合理的草地管理方式。因此，对土壤状态的准确预测对于草原的可持续保护和合理开发至关重要。本文通过对历年统计数据的分析，首先通过Softmax逻辑回归模型，结合处理后的数据，得到六种土壤状态与不同放牧策略的四分类模型，建立了不同放牧策略对草原土壤状态影响的数学模型。然后使用LSTM模型并基于多年份同放牧强度和放牧小区的土壤不同状态下的数据来进行训练，预测得到2023年的同条件下的土壤在不同状态下的数据。再利用沙漠化程度指数预测模型和数据来确定不同放牧强度下监测点的沙漠化程度数值。最后使用有机量、含水量、叶面积指数等指标代替用于衡量土壤状态的指标，有土壤肥力变化、土壤湿度、植被覆盖等，综合2014~2022年的土壤数据，使用LSTM模型预测得到2024年同月的土壤状态数据。

Abstract: China is a resource-rich country with abundant grassland areas. These grassland ecosystems serve as crucial barriers to maintaining the ecological balance in the country while providing a stable foundation for economic development. However, with the rapid expansion of livestock farming, the issue of grassland degradation has become increasingly prominent, even manifesting desertifica-tion trends in certain regions. Faced with this situation, there is an urgent need to establish scien-tifically sound grassland management approaches. Therefore, accurate prediction of soil conditions is crucial for the sustainable protection and rational development of grasslands. This paper analyz-es historical statistical data and employs a Softmax logistic regression model to establish a four-class model for the impact of different grazing strategies on six soil conditions. This model is based on processed data, providing insights into the influence of various grazing strategies on grassland soil conditions. Subsequently, an LSTM model is utilized and trained on data from multi-ple years with consistent grazing intensities and different soil conditions in grazing zones, to predict soil conditions in 2023 under the same conditions. Utilize a Desertification Severity Index Predic-tion Model and data to determine the degree of desertification at monitoring points under different grazing intensities. Finally, employing indicators such as organic matter, moisture content, and leaf area index as substitutes for metrics measuring soil conditions like soil fertility changes, soil mois-ture, and vegetation cover, the LSTM model, incorporating comprehensive soil data from 2014 to 2022, predicts soil condition data for the same months in 2024.

1. 引言

草原生态系统作为陆地生态系统的重要组成之一，植被类型分布广泛，是我国生态安全和食品安全的关键支柱。放牧优化问题是防止草原沙漠化的关键。过度放牧由于牲畜密度过大可能导致土壤裸露面积增加，对土地内水分相对运动产生不利影响，使土壤盐碱度程度增加，最终引发土壤沙漠化。相反，适度的放牧有助于提升土壤的状态，促进草原生态系统的可持续发展。放牧优化问题的研究也为国家、政府制定放牧政策和草原管理决策提供科学的依据 [1] [2] 。因此，预测不同放牧策略(放牧方式和放牧强度)对草原土壤性质的影响是非常有必要的。本文基于土壤有机碳数据、无机碳、全N以及土壤C/N比等值等信息，通过衡量土地状态的指标，土壤肥力变化、土壤湿度、植被覆盖等评估了土壤各性质对环境影响的响应程度。利用统计年鉴2014~2022年的数据，建立模型预测2023年在不同放牧策略(放牧方式和放牧强度)的情况下，使用LSTM法进行学习并对2024年九月的土地状态进行预测。

2. 模型建立与求解

本文用到的符号及其含义如表1所示。

2.1. Softmax模型

针对问题中建立不同放牧策略(放牧方式和放牧强度)对锡林郭勒草原土壤化学性质影响的数学模型，首先需要通过逻辑回归方法来判断不同放牧策略对锡林郭勒草原土壤化学性质变化的发生概率大小，进一步通过Softmax模型获得四种土壤化学性质与不同放牧策略的四分类模型的权重值以及相应分类模型的常数值。

Table 1. Symbol description

表1. 符号说明

2.1.1. Softmax建模

Softmax模型事实上式逻辑回归(Logistics)模型的推广，Softmax总目标是多分类，也是在多元线性回归基础上把结果缩放到0到1之间。然后依据属于哪一类的概率最高，选择该类，其中线性回归函数的数学表达式：

$y={\theta }_0+{\theta }_1{\chi }_1+{\theta }_2{\chi }_2+\cdots +{\theta }_n{\chi }_n={\theta }^{\text{T}}\chi$ (1)

其中 $x_i$ 是自变量， $y$ 是因变量， $y$ 的值域为 $\left(-\infty ,\infty \right)$ ， ${\theta }_i$ 是常数项， ${\theta }_i\left(i=1,2,\cdots ,n\right)$ 是待求系数，不同的权重 ${\theta }_i$ 反映了自变量对因变量不同的贡献程度。

Softmax模型：

${\hat{y}}^i=h_{\theta }\left(x^i\right)=\left[\begin{array}{c}P\left(y^i=1|x^i,q\right)\\ \\ P\left(y^i=2|x^i,q\right)\\ .\\ .\\ .\\ .\\ .\\ P\left(y^i=k|x^i,q\right)\end{array}\right]=\frac{1}{{\displaystyle \underset{j=1}{\overset{k}{\sum }}{\text{e}}^{-{\theta }_j^{\text{T}}{x}^i}}}\left[\begin{array}{c}{\text{e}}^{-{\theta }_1^{\text{T}}{x}^i}\\ \\ {\text{e}}^{-{\theta }_2^{\text{T}}{x}^i}\\ .\\ \cdot \\ \cdot \\ \cdot \\ \cdot \\ {\text{e}}^{-{\theta }_k^{\text{T}}{x}^i}\end{array}\right]$ (2)

$\hat{y}$ 值：概率含义( $\hat{y}$ 越大说明该例概率越大)。

Softmax回归模型如下图1所示。

2.1.2. 模型结果

首先需要通过逻辑回归方法来判断不同放牧策略对草原土壤化学性质变化的发生概率大小，如表2所示。表中数据的出重度放牧“3”准确率最大，中度放牧“2”准确率最低。

通过求解Softmax模型获得不同放牧策略对锡林郭勒草原土壤化学性质变化的概率权重，即四分类模型系数如下：

$\left[\begin{array}{cccccc}\text{0}\text{.18749361}& -\text{0}\text{.08152382}& \text{0}\text{.18908695}& -\text{1}\text{.7968938}& \text{0}\text{.04560131}& \text{0}\text{.12562905}\\ -\text{0}\text{.01772552}& \text{0}\text{.00408382}& \text{0}\text{.05685388}& \text{0}\text{.19276374}& \text{0}\text{.00868464}& \text{0}\text{.32389637}\\ \text{0}\text{.01157313}& \text{0}\text{.01591795}& -\text{0}\text{.1700262}& -\text{0}\text{.52627501}& -\text{0}\text{.00860049}& -\text{0}\text{.32719223}\\ -\text{0}\text{.18134122}& \text{0}\text{.06152205}& -\text{0}\text{.07293821}& \text{2}\text{.13040507}& -\text{0}\text{.04568546}& -\text{0}\text{.12233319}\end{array}\right]$

其中每个分类模型所含常数项如下：

$\left[\begin{array}{cccc}-\text{6}\text{.24012973}& -\text{2}\text{.86237095}& \text{5}\text{.54929601}& -\text{0}\text{.60797045}\end{array}\right]$

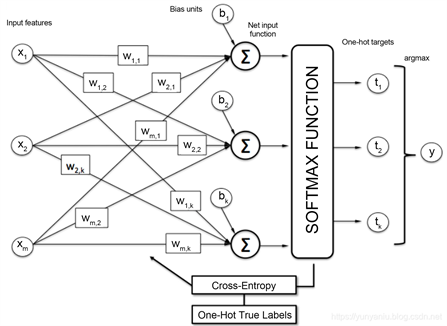
Figure 1. Softmax logistic regression model

图1. Softmax建模流程

Table 2. Regression model accuracy results

表2. 回归模型精度结果

2.2. LSTM模型

针对解决统计数据预测草原监测样地(12个放牧小区)在不同放牧强度下2023年土壤同期有机碳、无机碳、全碳、全N、土壤C/N比等值的问题。首先建立不同放牧强度和土壤化学性质数学模型，进而通过模型去预测2023年土壤化学性质数据。

LSTM模型，本质上是一种特定形式的循环神经网络(RNN)，主要是为了解决长序列训练过程中的梯度爆炸或梯度弥散问题 [3] [4] 。简单来说，就是相比普通的RNN，LSTM能够在更长的序列中有更好的表现。LSTM模型在RNN模型的基础上通过增加门限来解决RNN短期记忆的问题，使得循环神经网络能够真正有效地利用长距离的时序信息。

2.2.1. LSTM建模

LSTM在RNN的基础结构上增加了输入门限(Input Gate)、输出门限(Output Gate)、遗忘门限(Forget Gate) 3个逻辑控制单元，且各自连接到了一个乘法元件上，其概念图如下，通过设定神经网络的记忆单元与其他部分连接的边缘处的权值控制信息流的输入、输出以及细胞单元(Memory cell)的状态。其具体结构如下图2所示。

Figure 2. LSTM conceptual diagram

图2. LSTM概念图

上图中相关部件的描述如下：

Input Gate：用于控制信息是否流入记忆单元

Forget Gate：用于控制上一时刻记忆单元中的信息是否积累到当前时刻的记忆单元中

Output Gate：用于控制当前时刻的输出值，通过使用激活函数来评估当前输入和记忆状态的组合

cell：记忆单元，即神经元状态的记忆，它使得LSTM单元具有保存、读取、重置和更新长距离信息的能力。

隐藏层cell结构如下图3所示，在LSTM神经网络的训练过程中，首先将t时刻的数据特征输入至输入层，经过激励函数输出结果。将输出结果、t − 1时刻的隐藏层输出和t − 1时刻cell单元存储的信息输入LSTM结构的节点中，通过Input Gate，Output Gate，Forget Gate和cell单元的处理，输出数据到下一隐藏层或输出层，输出LSTM结构节点的结果到输出层神经元，计算反向传播误差，更新各个权值。

Figure 3. LSTM detailed diagram

图3. LSTM细节图

2.2.2. LSTM预测结果

进行预测锡林郭勒草原监测样地(12个放牧小区)在不同放牧强度下2023年土壤同期有机碳、无机碳、全碳、全N，而土壤C/N比等值可以通过预测所得的数据进行解算可得。LSTM模型原理是：通过多年份同放牧强度和放牧小区的土壤化学性质数据去预测未来某年的同条件下的土壤化学性质数据，并不断回头改进模型准确性。

以2014~2022年放牧小区为：G20、放牧强度为：重度放牧强度为例，展示其LSTM模型训练的准确度。模型的训练集和测试集比例为7:3。其训练结果如图4所示，其土壤化学性质均方根误差均在0.31以下，模型准确(表3)。

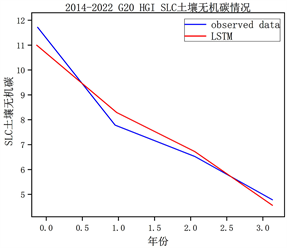
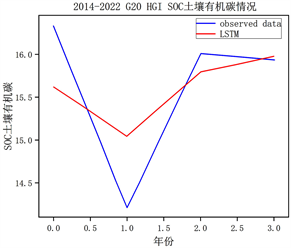(a) SOC土壤有机碳 (b) SIC土壤无机碳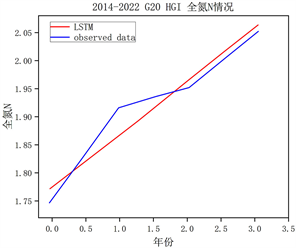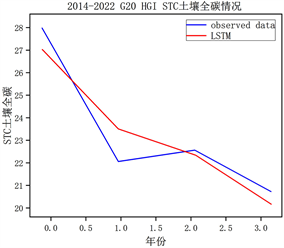(c) STC土壤全碳 (d) N全氮

Figure 4. LSTM training results

图4. LSTM训练结果

Table 3. Training error of soil chemical properties under heavy grazing intensity in the G20 region

表3. G20区重度放牧强度的土壤化学性质训练误差

采用以上LMST所得准确模型对2023年不同放牧强度和小区的土壤同期有机碳、无机碳、全碳、全N进行预测，计算土壤C/N比并完成下表4。

Table 4. Soil chemical properties prediction results

表4. 土壤化学性质预测结果

3. 沙漠化程度指数与土壤板结化定义

首先需要利用沙漠化程度指数预测模型和数据来确定不同放牧强度下监测点的沙漠化程度数值。通过查阅沙漠化预测公式的来源，确定各指标因子，并查阅锡林郭勒盟年鉴获取缺失的因子数据，计算因子强度，使用层次分析法计算各因子权重，从而计算不同放牧强度下的沙漠化程度指数。

使用因子分析法，对可能的造成土壤板结化的成分进行综合归纳，对各成分提出相应解释从而量化土壤的板结化指数，根据量化模型寻找使土壤板结化程度最小的放牧策略。

3.1. 沙漠化程度指数预测模型

3.1.1. 数据补充与计算因子强度Q_i

沙漠化的相关影响因素如图5所示，有气象因素：风速、降水、气温；地表因素：植被盖度、地表水资源、地下水位；人文因素：人口数量、牲畜数量、社会经济水平。将平均气温作为气温数据、将平均风速作为风速数据、将降水量作为降水数据；由于年鉴中地表水资源和地下水位的每年资料不全，这里将200 cm湿度作为地下水位数据、将10 cm湿度作为地表水资源数据、将植被指数作为植被盖度数据；通过查阅年鉴数据，将每年的总人口数量作为人口数量数据、将每年6月末及12月末的牲畜数量作为牲畜数量数据、将每年的全体居民人均可支配收入作为社会经济水平数据。

Figure 5. Factors influencing desertification early warning indicators

图5. 沙漠化预警指标影响因素

通过表5因子强度上限和下限以及因子强度(Q_i)的计算方法，对附件中的数据进行处理计算，将其投射为0~1的归一化数据，表6展示了部分因子强度Q_i的计算结果。

Table 5. Upper and lower limits of factor intensity

表5. 因子强度的上限和下限

Table 6. Partial calculation results of factor intensity Qi

表6. 部分因子强度Q_i计算结果

3.1.2. 层次分析法计算因子权重W_ci

层次分析法(AHP)将需要决策的复杂问题分解成不同层次和若干因素，通过两两比较确定层次中诸因素的相对重要性，是一种定性和定量相结合的多目标决策方法 [5] [6] 。土壤板结化属于多目标、多准则以及无结构特性的复杂决策问题，因此，可以应用该方法解决。通过AHP构建判断矩阵结果如表7，最终计算相关因素因子权重如下表8~10所示。

Table 7. Three-Factor decision matrix

表7. 三因素判断矩阵

Table 8. Weights of meteorological factor factors

表8. 气象因素因子权重

Table 9. Weights of surface factor factors

表9. 地表因素因子权重

Table 10. Weights of human factor factors

表10. 人文因素因子权重

3.1.3. 沙漠化程度指数计算结果

沙漠化程度指数预测模型表达式：

$SM=\eta \cdot {\displaystyle \underset{i=1}{\overset{n}{\sum }}{S}_{Q_i}}=\eta \cdot {\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(Q_i\cdot W_{ci}\right)}$ (3)

式中：SM表示沙漠化程度指数；η为调节系数，用来修正模型；n为模型中因子的个数；Q_i为第i个因子的因子强度； $S_{Q_i}$ 为第i个因子对沙漠化程度的贡献值； $x_1,x_2,x_3$ 为因子权重系数，即因子对沙漠化程度的贡献值等于因子强度与因子权重系数的乘积。

根据AHP法得到的各因素因子权重去计算沙漠化程度指数，下表11仅展示部分数据。

Table 11. Desertification severity index

表11. 沙漠化程度指数

3.2. 土壤板结化定量分析

土壤板结化与土壤有机物、土壤湿度和土壤的容重有关，目前还没有明确的定量表达式，其数学模型可定性描述为如下：

$B=f\left(W,C,O\right)$ (4)

土壤湿度W越少，容重C越大，有机物含量O越低，土壤板结化程度B越严重。

性质和物理性质是影响土壤肥力重要因素，土壤化学性质包括：土壤有机碳SOC、土壤无机碳SIC、土壤全碳STC、全N、土壤C/N比等；土壤物理性质包括：土壤湿度、土壤容重等。

使用因子分析将这些错综复杂的变量对影响土壤板结化关系归结成几个综合因子，并确定其模型。

3.2.1. 因子分析

假设大小为 $n\times p$ 的随机向量 $x={\left(x_1,x_2,\cdots ,x_p\right)}^{\prime }$ 的均值 $u={\left(u_1,u_2,\cdots ,u_p\right)}^{\prime }$ ，协方差矩阵 ${\Sigma }_{p\times p}=\left({\sigma }_{ij}\right)$ ，因子分析的一般模型为：

$\{\begin{array}{c}{x}_1=u_1+a_{11}{f}_1+a_{12}{f}_2+\cdots +a_{1m}{f}_m+{\epsilon }_1\\ x_2=u_2+a_{21}{f}_1+a_{22}{f}_2+\cdots +a_{2m}{f}_m+{\epsilon }_2\\ \cdot \\ .\\ \cdot \\ \cdot \\ \cdot \\ x_p=u_{p1}{f}_1+a_{p2}{f}_2+\cdots +a_{pm}{f}_m+{\epsilon }_p\end{array}$ (5)

其中 $f={\left(f_1,f_2,\cdots ,f_m\right)}^{\prime }\left(m\le p\right)$ 为公共因子， $\epsilon ={\left({\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_p\right)}^{\prime }$ 为特殊因子，两者皆为无法观测的随机变量。同时根据 $x=u+Af+\epsilon$ 构造如下式假设：

$\{\begin{array}{c}E\left(f\right)=0\\ E\left(\epsilon \right)=0\\ Var\left(f\right)=I\\ Var\left(\mathcal{E}\right)=D=didg\left({\sigma }_1^2,{\sigma }_2^2,\cdots ,{\sigma }_e^2\right)\\ \mathrm{cov}\left(f,\mathcal{E}\right)=E\left(f{\mathcal{E}}^{\prime }\right)=0\end{array}$ (6)

公因子其具有单位方差且彼此不相关，特殊因子则不仅自身彼此不相关，与公因子也不相关。

3.2.2. 因子分析结果

结合图6碎石图和表12成分总方差数据可知，影响土壤板结化的前四个因子影响占比高达85.163%，其影响数值足以用四个成分代表整体，故这里选用四个未知成分去解释土壤板结化模型。

确定的成分数量已确定，然后针对土壤有机物、土壤湿度、土壤的容重以及沙漠化程度指数相关因子进一步获得其影响土壤板结化成分得分系数矩阵，如表13所示，每种成分因子所占四个主成分权重可以知道其归属于第几主成分，第一主成分(SOC土壤有机碳、全氮N、土壤C/N比)；第二主成分(10 cm土壤湿度、40 cm土壤湿度、100 cm土壤湿度)；第三主成分(SIC土壤无机碳、STC土壤全碳)；第四主成分(200 cm土壤湿度、沙漠化程度指数)。

进一步可以对四个成分进行解释，分别为有机量、含水量、含碳量、干燥度。

Figure 6. Gravel map

图6. 碎石图

Table 12. Total variance of components data

表12. 成分总方差数据

Table 13. Component score coefficient matrix

表13. 成分得分系数矩阵

3.2.3. 定量模型

通过上述因子分析的结果，可以通过前四主成分占比总量去调整其权重：第一主成分(0.4741)；第二主成分(0.258)；第三主成分(0.1569)；第四主成分(0.111)。四个成分已做说明，分别为有机量、含水量、含碳量、干燥度。故土壤板结化定量模型如下式：

$B=0.4741O_c+0.258M_w+0.1569M_c+0.111D_w$ (7)

式(7-5)中：B表示土壤板结化； $O_c$ 表示有机量； $M_w$ 表示含水量； $M_c$ 表示含碳量； $D_w$ 表示干燥度。

3.3. 放牧策略模型结果

通过上述得到的沙漠化程度指数模型和量化的土壤板结化指数模型进行联立，见下式：

$\{\begin{array}{l}SM=\eta \cdot {\displaystyle \underset{i=1}{\overset{n}{\sum }}{S}_{Q_i}}=\eta \cdot {\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(Q_i\cdot W_{ci}\right)}\\ B=0.4741O_c+0.258M_w+0.1569M_c+0.111D_w\\ \left\{C_l\right\}=\min \left\{SM+B\right\}\end{array}$ (8)

式中： $\left\{C_l\right\}$ 表示使沙漠化程度指数与板结化程度最小的相关因素的集合。通过模型求解最终可获得 $\left\{C_l\right\}$ 相关集合，提取集合中的放牧小区和放牧强度因素，最终确定使土壤板结化指数最小的放牧策略见下表14：

Table 14. Grazing strategy results

表14. 放牧策略结果

3.4. LSTM预测

要预测放牧区2023年九月的土地状态，衡量土地状态的指标有土壤肥力变化、土壤湿度、植被覆盖等。此处使用对土壤板结化进行因子分析后综合得出的指标来替代，将有机量作为土壤的肥力，将含水量作为土壤湿度，将叶面积指数作为植被覆盖。沿用上面的LSTM建模方法，综合2014~2022年九月的土壤数据，使用LSTM法进行学习并2023年九月的土地状态进行预测。

预测结果

2014~2022年九月有机量、含水量和叶面积指数LSTM模型的训练集和测试集比例为7:3，其训练结果如表15、图7所示。三种土地状态指标的RMSE值均在0.62以下、MAE值不超过4.5，因此模型准确。

Table 15. Model training error

表15. 模型训练误差

通过上述所建立的LMST模型进行2024年九月的土地状态的预测，如图8所示。蓝色点表示2014~2022年九月的土地状态，绿色点表示这几年的平均值，红色点为预测得到的2024年九月的土地状态。可以看出2024年的土壤，其植被盖度和土壤湿度得到了改善，而相应的，土壤的肥力会下降。

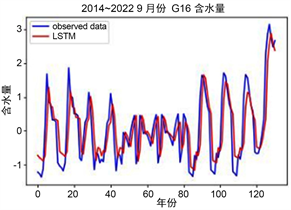
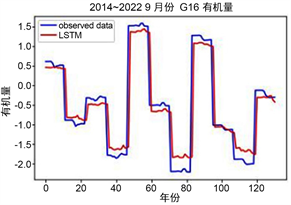(a) 有机量 (b) 含水量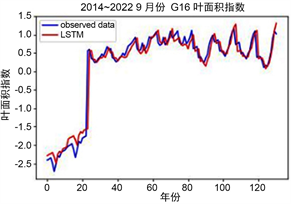(c) 叶面积指数

Figure 7. LSTM model training results

图7. LSTM模型训练结果

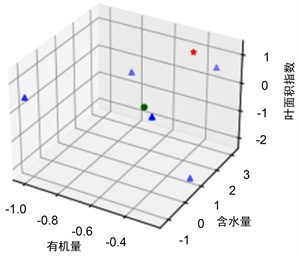
Figure 8. Soil condition in September 2024

图8. 2024年9月的土壤状态

4. 结论

综合以上分析，本研究通过Softmax逻辑回归模型和LSTM模型，成功建立了草原土壤状态与放牧策略的预测模型。通过对历年统计年鉴数据的深入分析，我们得出了六种土壤状态在不同放牧策略下的四分类模型，并通过LSTM模型预测了2023年的土壤状态数据。沙漠化程度指数的运用进一步确定了监测点在不同放牧强度下的沙漠化程度数值。最后，我们采用了有机量、含水量、叶面积指数等多指标代替传统的土壤肥力、土壤湿度、植被覆盖等指标，综合分析2014~2022年的土壤数据，并通过LSTM模型成功预测了2024年同月的土壤状态数据。这些预测结果为草原的可持续保护和科学合理开发提供了重要的参考，为未来的草原管理和决策制定提供了可靠的数据支持。