随机振动条件下的电池架的响应分析

Response Analysis of the Battery Box Bottom under Random Vibration Conditions

摘要: 为提高电动汽车电气结构在振动载荷下的安全性和可靠性，本研究建立了电池架的三维有限元模型。采用ANSYS软件，按GJB 150.16-86标准对模型在三个正交方向(纵向的X轴、横向的Y轴和垂直的Z轴)进行随机振动仿真分析。结果显示：在X轴和Y轴方向，电池架变形很小，不超过0.2毫米，说明其在这两个方向具有良好的刚性；在Z轴方向，电池架的变形相对较大，达到5毫米左右，但预示装填电池后其刚性会得到增强并减小变形；经历随机振动后，电池架的最大应力为3.57兆帕，远远低于材料的屈服极限，证实了电池架结构的完整性。综上结果表明，该电池架设计满足了强度和耐久性要求，确保了其结构在随机振动条件下的可靠性，为电动汽车电气系统的安全性提供保障。本研究建立的模型和方法可推广应用于其他电池系统的动力学分析与评估。

Abstract: In order to improve the safety and reliability of electric vehicle electrical structures under vibration loads, this study established a three-dimensional finite element model of the battery frame. Using ANSYS software, the model was subjected to random vibration simulation analysis in three orthog-onal directions (longitudinal X-axis, lateral Y-axis, and vertical Z-axis) according to the GJB 150.16-86 standard. The results showed that: in the X-axis and Y-axis directions, the deformation of the battery frame was very small, no more than 0.2 mm, indicating good rigidity in these two direc-tions; in the Z-axis direction, the deformation of the battery frame was relatively large, reaching around 5 mm, but this implied its rigidity would be enhanced and deformation reduced after bat-teries were loaded; after random vibration, the maximum stress on the battery frame was 3.57 MPa, far below the material’s yield limit, confirming the integrity of the frame structure. In summary, these results demonstrate that the battery frame design meets the strength and durability re-quirements, ensuring structural reliability under random vibration conditions and safeguarding the safety of electric vehicle electrical systems. The model and methodology established in this study can be extended to the dynamic analysis and evaluation of other battery systems.

1. 引言

在当前的纯电动汽车技术浪潮中，汽车电池显得尤为重要。电池作为电动汽车的核心储能部件，其电池架在面对高温、振动和冲击等恶劣条件时的性能表现，直接关系到电池的整体安全和使用寿命 [1] 。因此，通过高效的结构仿真来分析电池架的响应特性，成为了确保电动汽车安全的一个重要环节。

随机振动条件下的电池架响应分析尤为重要，它涉及到电池架在实际道路行驶过程中可能遇到的各种复杂振动情况。近年来，许多研究者已经通过有限元分析来评估电池架的结构安全性。例如，赵久志 [2] 等人建立的动力电池总成的三维实体模型和XIA Yong [3] 等人对锂离子电池箱碰撞的研究，都为我们提供了宝贵的参考。特别是吉林大学李明秋 [4] 的工作，他在ANSYS Workbench平台上建立了电池架的三维实体有限元模型，并进行了机械冲击、模态和随机振动分析，对电池架的结构设计提出了改进建议。

在这一研究领域，我们的工作旨在进一步探索电池架在随机振动条件下的响应特性。我们的目标是通过结合极限和实际工况，使用仿真技术来模拟和分析电池架在不同条件下的响应，从而为电池架的改进提供重要的理论基础。

为了深入探究纯电动汽车电池架在复杂环境下的性能，本文基于现有数据构建了电池架的三维有限元模型。采用ANSYS软件对其进行了随机振动模拟和分析，以提供更精确的数据评估。模拟遵循GJB 150.16-86军用标准 [5] ，考虑了电池架在三个正交方向(x轴、y轴和z轴)的动力学响应。这种全方位模型的建立使我们能够进行模态和随机振动响应的深入分析。该分析有助于确保电池架在实际使用环境下的可靠性和稳定性，保证军用设备的正常工作。

2. 随机振动分析

根据振动理论，我们知道在线性响应范围内，每个运动微分方程都对应特定频率的自由振动。当结合N个运动微分方程时，共同定义了该结构的固有频率，动力学模型可表示为：

$m\ddot{x}\left(t\right)+c\stackrel{\dot{}}{x}\left(t\right)+kx\left(t\right)=F(\; t\; )$

式中：x(t)是时间t下的位移，F(t)表示作用在系统上的外力。通过求解运动方程，可以得到系统对外界激励的动态响应，为电池架的动态设计和分析奠定理论基础。

系统对外部激励F(t)的响应可以通过以下公式获得：

$x\left(t\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\gamma }_i{\varphi }_i{q}_i(\; t\; )}$

式中， $q_i\left(t\right)$ 是第i个模态的广义坐标， ${\gamma }_i$ 为模态参与因子。

若F(t)为随机过程，其功率谱密度函数为 $S_Y\left(\omega \right)$ ，则第i个模态的响应的功率谱密度函数为：

$S_{q_i{q}_i}\left(\omega \right)={\left|H_i\left(\omega \right)\right|}^2{S}_Y(\; \omega \; )$

综合所有模态，即可得系统的总响应功率谱密度函数为：

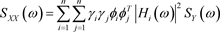
3. 建立电池架仿真模型将模型导入到ANSYS Workbench中，选用随机振动分析模块进行深入研究。在材料上选用丙烯腈/丁二烯/苯乙烯共聚物(ABS)，以确保模型的韧性和耐冲击性。对整体结构进行网格划分处理，如图1所示。在网格划分方面，我们选择了以四边形为主、三角形为辅的策略，以期望获得更小的误差和更高的计算精度。我们选择了单元网格边长为5 mm的四边形进行划分。这种划分在确保精度的同时，也便于后续的网格修正和质量检测。此外，根据工况的需求，电池架的下平面被设定为约束条件，如图2所示，从而模拟实际使用中的状态。

Figure 1. Meshing models

图1. 网格化模型

Figure 2. Add constraints

图2. 添加约束

经过网格划分后，我们依照表1中的单元质量检查规范，对生成的网格质量进行了检测与优化。优质的网格结构能够更好地模拟电池架在实际运行中可能遇到的各种振动和应力条件，通过不断调整网格参数，获得符合质量标准要求的计算网格。这一步的目的是确保网格质量达到预期目标，为后续的随机振动分析奠定坚实的基础 [6] 。

Table 1. Unit quality check specification

表1. 单元质量检查规范

本研究选择ABS树脂作为电池架的主要材料。ABS树脂具有优异的机械性能，包括高强度、良好的韧性和耐冲击性。同时，ABS材料密度较低，加工制造简便，成本效益高。这些特性使其非常适合在需要承受随机振动和撞击载荷的部件中使用。本研究选用的ABS材料主要性能参数见表2。这些精确的材料数据，包括弹性模量、抗拉强度等，将确保数值仿真的准确性。与金属材料相比，ABS材料更轻，也更容易通过注塑成型获得复杂形状，这对于电池架的整体结构优化具有重要意义。综上，ABS树脂是设计随机振动环境下电池架的理想选择。

Table 2. Material properties

表2. 材料属性

4. 模型分析

4.1. 求解准备

在对电池架进行随机振动响应分析之前，首先采用模态分析方法提取其动态特性。模态分析能够确定结构的自然频率和振型，这对理解和预测结构对动态载荷的响应至关重要。通过模态分析得到的参数为后续的随机振动分析奠定了基础 [7] 。随机振动分析可以预测在复杂随机激励下结构的响应统计特性，评估结构的耐久性和安全性。本研究配合使用这两种分析方法，首先通过模态分析确定电池架的动态特性，再基于模态分析结果开展随机响应分析，评估电池架在实际工作环境中的动态行为。

随机振动分析中一个核心概念是功率谱密度(PSD)，它描述了作用在结构上的随机动态载荷所含能量分布的统计特征。本研究中所采用的随机振动PSD参考了GJB 150.16-86标准，具体参数见图3所示。该军用标准提供了随机振动试验的详细数据依据。我们分别提取了该标准规定的水平和垂直两个方向的PSD曲线(图3(a)和图3(b))，作为输入激励加载应用到电池架结构上，开展后续的随机响应分析。选用权威标准作为加载输入的依据，有助于保证分析结果能够反映实际工程问题，评估结构在典型随机振动环境下的动态响应和耐久性能。

4.2. 求解过程

4.2.1. 模态分析

鉴于本研究采用的军用标准GJB 150.16-86中规定的随机振动功率谱密度分析的频率上限为200 Hz，

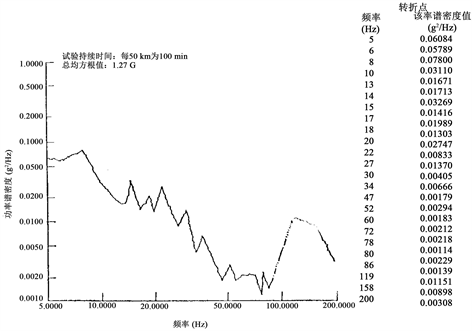(a) 水平方向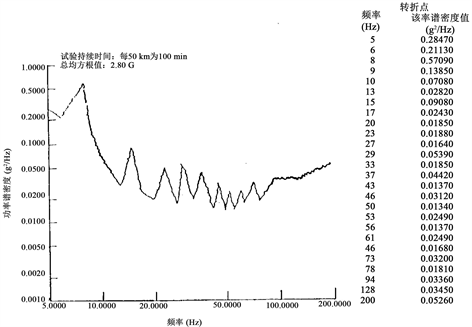(b) 垂直方向

Figure 3. GJB 150.16-86 random vibration

图3. GJB 150.16-86随机振动

进行完整频率范围的响应计算将带来较大量计算量。一般来说，对于汽车电池架结构，外界随机动态激励对模型较低阶模态的影响最为主要 [8] 。经工程经验统计，计算前6阶固有频率模态基本可以达到工程计算要求，计算前10阶固有频率结果可以保证计算精度，为求得精确可靠的分析结果，本研究选取前15阶固有频率进行详细分析，该选择综合考虑了计算量和结果准确性 [9] 。

通过精确的模态分析计算，我们得到了电池架在0~200 Hz范围内的前15阶模态频率分布，如图4所示。此模态分析的目的是为了详细揭示电池架结构在典型工作环境中可能遇到的低频激励下的动力学特性。模态分析结果中提取的电池架各阶模态的固有频率和对应振型模式，为后续的随机振动响应分析奠定了基础。这些模态参数可用于建立精确的结构动力学模型，预测和评估电池架在随机动态载荷下的动态响应、结构安全性和使用可靠性。

Figure 4. Modal analysis results

图4. 模态分析结果

在完成前15阶模态分析后，我们描绘并获得了电池架结构在0~200 Hz范围内的频率响应特性。基于这一模态分析结果，我们进一步利用提取的模态参数数据，结合所选定的随机振动功率谱密度加载，开展随机响应分析。具体而言，该分析对应将各模态的频率响应函数与输入的随机激励能量密度分布相协调，评估电池架在复杂随机动态激励下的振动响应性能。通过这一方法，我们可以全面预测和评价该结构在各种实际工作环境中可能遭遇的复杂动态载荷下的动力学响应，为结构优化和可靠性设计提供参考。

4.2.2. 添加功率谱

完成前15阶模态分析后，本研究于随机振动响应计算中引入功率谱密度(PSD)加载。在载入模态分析结果的基础上，随机分析采用PSD数据激励结构，评估电池架在不同随机动力学激励下的响应统计特征。本研究PSD载荷选用军用标准GJB 150.16-86中规定的数据，其中包含的频率范围和能量分布信息，确保所得分析结果适用性强和计算可靠性高。鉴于数据量庞大，本文仅展示了部分数据(见表3)。完整和详尽的数据集可参考GJB 150.16-86标准文档，本次研究中将完整数据输入到ANSYS中绘制为功率谱密度曲线，如图5所示。通过结合模态参数和标准PSD激励，可准确预测分析电池架结构在实际复杂随机振动环境下的动力学响应，满足工程设计优化需求 [10] 。

4.2.3. 查看变形结果

在对电池架结构进行随机响应分析并加载标准PSD数据后，我们通过ANSYS Workbench仿真结果查看和分析了电池架在三个主要方向(X、Y、Z)上面的位移响应。图6~8分别展示了电池架顶部在这三个方向上的结构变形效应。这些随机响应动力学分析直观地反映了电池架顶部在实际复杂工作条件下的位移和变形情况，为后续电池架结构的优化设计和加固改进提供了依据。

Table 3. GJB 150.16-86 partial data

表3. GJB 150.16-86部分数据

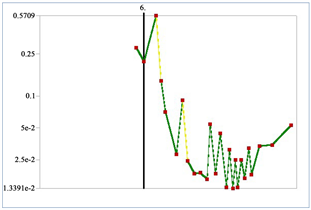
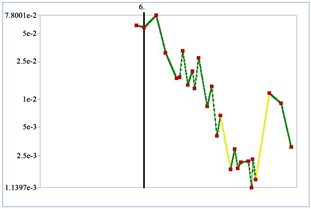(a) 水平方向 (b) 垂直方向

Figure 5. Add the power spectral density

图5. 添加功率谱密度

Figure 6. X-axis direction

图6. X轴方向

图6~8展示了电池架在经过随机响应分析后的三个主要方向(X、Y、Z轴)上的位移变形效应。第一张图揭示了X向最大变形约为0.2 mm。第二张图显示Y向最大变形略高于X向。第三张图中，Z轴即垂直方向上的最大变形量显著增加至5 mm左右，远高于其他两个方向且发生在电池架顶部。结果表明，在复杂随机振动载荷下，电池架顶部结构在垂直方向(Z轴)耐振动性能较为薄弱。上述三个方向的位移响应统计参数，为评估和设计电池架顶部结构在实际工况下的动力学性能提供了关键依据。特别是Z向的大位移反应，提示此方向需优先进行结构加固。

Figure 7. Y-axis direction

图7. Y轴方向

Figure 8. Z-axis direction

图8. Z轴方向

4.2.4. 查看应力结果

在完成电池架的随机响应位移分析后，我们进一步检查了其在复杂随机振动激励下的结构应力分布。应力响应分析是评估材料性能、预测疲劳和故障的关键。图9展示了电池架在进行随机振动模拟后顶部结构上的等效应力云图。这些模拟结果将为电池架的结构优化提供依据。

Figure 9. The stress on which the model is subjected

图9. 模型所受应力

图9直观展示了电池架顶部结构在随机振动作用下的等效应力云图。我们看到，电池架最大等效应力可达3.57 MPa，最小应力为175.77 Pa，其中最大应力区域并未发生在顶部结构中。通过对随机应力响应的校验，工程师可以评估结构强度匹配性，并据此确定是否需要针对应力集中区域进行电池架结构的二次优化设计，以满足安全和可靠性要求。

4.3. 结果分析

经过对电池架结构的全面随机振动分析，我们获取了电池架在三个主要方向(X/Y/Z轴)上的精细化位移响应和应力分布数据。结果显示，X轴和Y轴方向上位移响应极小，最大变形均在0.2 mm之下，说明电池架在水平面内具有良好的刚性。另外，Z轴方向(垂直向)的最大位移为5 mm，相对较大，但考虑到电池架实际工作状态下内部装有电池组，其整体刚性将得到改善，位移响应也将下降。此外，三个方向的最大等效应力均低于材料屈服极限。因此，复杂环境下的随机响应分析验证了该结构设计方案在强度、刚性和耐久性方面满足工程要求，为电池架的实际应用提供了可靠性保证。

5. 结论

本研究对电池架结构在随机振动激励下的动力学响应进行了详细分析，首先构建了自由振动的微分运动方程，随后通过模态分析建立了理论基础，并利用ANSYS工具进行了随机响应分析。分析结果显示，电池架在X轴和Y轴方向的动态响应符合要求，尽管Z轴(垂直方向)存在较大位移，但电池组的约束作用可以减轻这一问题。同时，最大应力水平远低于材料强度极限，确保了设计的安全性。本文的研究不仅为电池架结构的动力学性能评估提供了精确依据，还为相似结构的动力学设计和安全性校验提供了计算分析流程。