1. 引言
人脸识别是生物识别领域的研究热点之一,在身份认证 [1] 、访问控制 [2] 等领域具有广泛的应用。在过去的二十年里,许多学者提出了大量的人脸识别方法,包括最近邻方法 [3] 、字典学习 [4] 、主成分分析方法 [5] 和基于卷积神经网络的方法等 [6] 。
最近,基于回归的模型 [7] [8] [9] [10] [11] 已被广泛应用于处理人脸识别问题,并取得了有希望的结果。为了提高人脸识别的准确性,许多研究人员考虑了先验信息,如数据之间的相似关系或局部结构信息,并提出了不同的模型来解决人脸识别问题 [12] [13] 。
上述提到的模型可以从不同的角度提升人脸识别的性能。然而,这些模型都是基于一维像素级噪声的回归模型,都忽略了误差图像的结构信息。考虑到测试图像中的遮挡通常会导致低秩误差图像矩阵,并且秩最小化问题是NP难问题,许多研究人员提出了基于核范数的多种矩阵回归模型 [14] [15] [16] [17] [18] 。
从上述文献中,我们发现大多数现有的工作都考虑使用核范数回归模型来处理人脸识别问题。然而,如果人脸图像的遮挡区域变得更加显著,这些模型在实践中通常效率不高。因此,在本文中,我们提出了一种基于行稀疏的局部约束矩阵回归模型(RSLMR),以有效解决图像中不存在遮挡或者大面积遮挡的问题。
2. 模型建立
2.1. 研究动机
误差图像的行存在稀疏性:当测试图像不存在遮挡时,重建图像的像素值与测试图像非常接近,这意味着原始图像的每个像素都可以在重建图像中找到对应的像素,没有任何像素被遮挡或丢失。我们绘制了测试图像、重建图像和误差图像的所有像素值的曲线,如图1所示,重建图像的像素值与测试图像高度接近,而误差图像矩阵中的非零元素主要代表图像的噪声或细微差异。因此,在误差图像矩阵中,只有少数像素对重建图像的误差起到显著作用,而大多数像素的误差相对较小。我们假设误差图像矩阵的行具有稀疏性,即只有少数行对结果产生显著影响,而大多数行对结果影响较小。通过使用矩阵的
-范数,我们鼓励矩阵中的行稀疏性,促使重建图像在稀疏性的引导下,将重要的像素保留并减少噪声的影响,从而降低计算复杂度和提高模型的解释性。
重建图像与测试图像相似:在以往的矩阵回归模型中,通常只控制误差图像矩阵的低秩或稀疏性,这意味着恢复的重建图像矩阵可能是任意的,并且远离真实的测试图像矩阵。因此用这样一个任意的重建图像矩阵来训练模型并不有利于性能的提升。为了鼓励恢复的重建图像矩阵接近于真实的测试图像矩阵,我们期望,如果图像在特征空间中彼此接近,那么它们各自恢复的矩阵也应该彼此相似。即,我们对重建图像矩阵进行约束,使其图像内部的距离信息与测试图像内部的距离信息相似,从而对重建图像进行控制。
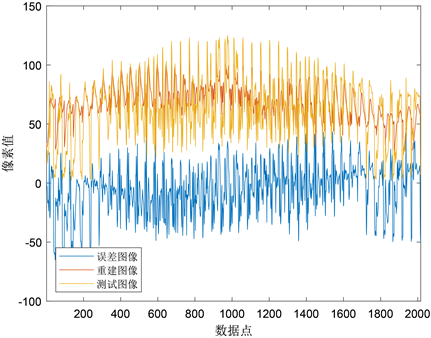
Figure 1. Pixel values of the test image, reconstructed image, and error image
图1. 测试图像、重建图像与误差图像的像素值
2.2. 模型构建与求解
首先基于第一个动机,RSLMR的初步目标函数可以描述如下:
其中
,
和
分别表示测试图像,重建图像和误差图像。
表示包含v个训练图像的矩阵。
是目标系数向量。
通过使一些行容易收缩到零来惩罚E中行的平方根。
表示矩阵D的向量形式。
基于第二点动机,我们在模型中添加一个正则化项来保持重建图像的局部结构:
其中,
表示第i行与第j行之间的相似性,计算结果为:
上式可以重新表述为
,其中L是
的拉普拉斯矩阵,
是一个对角矩阵,其中第i个对角元素是
第i行的和,
是
元素是
的矩阵。接着我们继续考虑使用误差图像矩阵行连续差的稀疏性,同时我们用同一类的样本的协作关系,并对不同类施加权重。因此最终的模型RSLMR如下:
(1)
其中
表示
向量的第j个值,即
。
、
、
和
是正的参数。
定义为:
其中
为第i类的训练图像数据矩阵,即
。
表示第i类的训练样本数,c表示训练样本中的类总数。
矩阵
和
的构造如下:
构造对角矩阵
,我们将第i类对应的元素设为1,而其余的元素设为0。并构造矩阵
,其中第i类对应的位置与
相同,矩阵中其他位置均为0。
通过引入新的变量,(1)可以改写为:
(2)
为求解方便,我们引入新的变量
与
,将(2)改写为:
(3)
为了求解(3),我们采用交替方向乘子法(ADMM)算法,首先给出(3)的增广拉格朗日函数:
其中
是一个惩罚参数,
,
,
与
是增广拉格朗日乘子。
我们通过以下步骤来更新每次迭代中的所有变量。
(步1) 首先求解E,固定其他变量,则E-子问题可以写作:
其中
。
是将向量转换为矩阵的运算符。
(步2) 在其他变量被固定后,则D-子问题可以写作:
(步3) 我们通过以下问题更新变量x,并利用一阶最优性条件,得到x的最优解:
(步4) 其次,
-子问题可以通过软阈值算子推导出:
其中
是软阈值算子。
(步5) 最后固定其他变量,求解U:
其中G是具有第i个对角线元素为
的对角矩阵。
最后拉格朗日乘子的更新如下:
停止标准定义为:
接下来我们将介绍分类标准。假设
是第i类的系数向量,
是第i类的训练图像数据矩阵,第i类的重构图像数据矩阵为
。最终的分类结果为
。
3. 数值实验
在本节中,我们将我们的模型RSLMR与LRC [7] ,CRC [9] ,SRC [8] ,GSC [10] ,NMR [14] ,SR_NMR [15] ,ENMR_RLS [18] 和LDMR [17] 进行了比较。在我们的模型中,我们将参数设置如下:
,
,
,
,
。我们的实验数据来自以下公开的数据库:FERET,ORL与CMU_PIE数据库。所有的数值结果都是在配备了i5-7200U 2.50 GHz CPU和20GB内存的笔记本电脑上使用MATLAB获得的。
FERET数据库包含了来自约1000名志愿者的14,126张人脸图像。这些图像涵盖了不同的人脸表情、姿势和光照条件。我们采用一个子集,其中包含了200个个体共1400张人脸图像。实验中所有图像大小被调整为48 × 42像素。
ORL数据库包含40人共400张面部图像。每个采集对象包含10幅经过归一化处理的灰度图像,图像尺寸均为92 × 112,图像背景为黑色。其中采集对象的面部表情和细节均有变化,不同人脸样本的姿态也有变化,其深度旋转和平面旋转可达20度。在实验中我们采用原始图像的像素,即仍为92 × 112。
CMU_PIE数据库包含68位志愿者的41,368张多姿态,光照和表情的面部图像。其中的姿态和光照变化图像是在严格控制的条件下采集的,目前已经逐渐成为人脸识别领域的一个重要的测试集。实验中所有图像大小被调整为48 × 42像素。
3.1. 光照条件下的人脸识别
当光照较暗时,测试图像中的像素值会受到限制。这意味着图像中的亮部区域可能会变得灰暗或接近黑色,像素值较低。这种情况下,误差图像中的像素值整体偏低。这导致误差图像矩阵行向量中的元素值较小,行向量的范数较小,甚至收缩为0。此时采用误差图像矩阵的
-范数使行收缩为0是合理的,它表示某些行对误差贡献较小或可以忽略。因此,在本节中,我们采用带有光照的CMU_PIE数据库来测试所有模型的性能。根据光照强度,我们将CMU_PIE数据库划分为6个子集。从子集1到子集6,人脸图像表现出从轻微到严重的光照变化。我们使用子集1用于训练,使用子集5和子集6用于测试。结果如表1所示。可以看出RSLMR模型在两个测试集上表现最好,平均识别率为93.2%。与LDMR相比,RSLMR在子集5和子集6上分别提高了12.87%和18.38%,与ENMR_RLS相比分别提高2.95%和4.78%。

Table 1. Recognition rates of all models on the CMU_PIE database
表1. 所有模型在CMU_PIE数据库上的识别率
随后我们固定训练集1,观察在测试集不同的情况下,所有模型的识别率。结果见表2所示,其中测试集1,测试集2,测试集3和测试集4分别包含个体的1,3,5,7张图像。可以看出RSLMR模型呈现出具有竞争力的结果,平均识别率为89%。在以上数据库的实验表明,RSLMR能识别光照下的图像。与核范数矩阵回归模型相比,RSLMR模型使用
-范数,这对异常值和噪声更加鲁棒。因为核范数是基于误差图像的奇异值,所以对误差图像中的异常值和噪声比较敏感。如果误差图像中存在个别异常值或噪声,核范数可能会受到它们的影响,导致结果不够稳定。
3.2. 无遮挡情况下的人脸识别
目前,在无遮挡情况下的人脸识别中,当每个个体的训练样本很多时,回归模型的识别率通常表现较好。因为面部的姿势、表情、光照条件等因素会导致人脸的外观变化,而多个训练样本可以提供更多的信息和多样性,使得模型能够更好地学习人脸的特征和变化。然而当每个个体的训练样本很少时,回归模型的识别率通常会受到限制。因此在本节中,我们评估所有模型在FERET数据库上的表现时,首先评估当训练图像个数变化而测试图像不变时各模型的识别率。

Table 2. Recognition rates of all models on the CMU_PIE database
表2. 所有模型在CMU_PIE数据库上的识别率
我们从每个个体的图像中随机选择1、3、5和6张图像分别作为训练集1、训练集2、训练集3和训练集4,并从每个个体的剩余图像中随机选择6、5、3和1张图像分别作为测试集1、测试集2、测试集3和测试集4。首先我们固定测试集4,观察当训练集不同时各模型的表现。结果如表3所示。从结果可以看出,当采用训练集4时,LDMR与RSLMR的识别率达到最高。原因是LDMR与RSLMR模型都利用了先验信息,当训练集图像较多时,这可以提高模型对训练集中的样本的辨别能力,进而提高识别率。而一维回归模型如LRC、SRC、CRC与GSC在训练图像较少时识别率反而较高,原因可能是这些模型在训练过程中会出现过拟合的情况,即模型过度拟合训练数据,在未见过的数据上表现较差。而且由于训练集图像较少,模型更容易记住每个样本的细节特征,从而在训练集1上表现较好。

Table 3. Recognition rates of different models on the FERET database with different training sets
表3. 在FERET数据库中,随着训练集的不同各模型的识别率
接下来我们固定训练集1,观察当测试图像数量不同时各模型的表现,结果如表4所示。可以看出,当测试图像数量逐渐增多时,LDMR与RSLMR的识别率的差异变得显著。当选取测试集1时,LDMR与RSLMR的识别率相差7.5%。当测试集数量逐渐增加时,模型的识别率呈现下降的趋势。因为训练集1只包含每个个体的一张图像,而模型的泛化能力非常有限,回归模型可能过度拟合了训练图像的细节特征,无法很好地适应新的测试图像。因此只有一张训练图像的训练集无法提供足够多样化的数据样本, 无法覆盖测试数据中的各种变化和特征。如果该图像包含异常值或噪声,模型可能会过度拟合这些异常值,导致对新的测试图像表现不佳。

Table 4. Recognition rates of different models on the FERET database with different test sets
表4. 在FERET数据库中,随着测试集的不同各模型的识别率
接下来我们在ORL数据上进行测试。我们随机选择每个个体的3张图像作为训练集,并在剩余的图像中随机选择3张图像与5张图像分别作为测试集1与测试集2。结果如表5所示,RSLMR模型取得了最好的结果,平均识别率为81.25%。对于两个测试集,各模型识别率之间差距不大。因为ORL数据库是一个相对较小且简单的人脸识别数据集,其图像在特征之间的差异相对较小。并且ORL数据库中不同类的人脸之间的差异明显,类之间的相关性较低。因此回归模型在这种数据集上能够轻松地捕捉到数据的特征,从而导致各模型的识别率差距不大。在无遮挡的图像中,人脸图像的大多数像素是准确的,只有少数像素受到误差的影响。因此,使用
-范数可以更好地捕捉到这种稀疏性。

Table 5. Recognition rates of all models on the ORL database
表5. 所有模型在ORL数据库上的识别率
4. 结论
这篇论文提出了一种用于人脸识别的基于行稀疏的局部约束矩阵回归模型(RSLMR)。该模型主要针对包含连续遮挡和无遮挡的人脸识别任务。以往的研究通常考虑到误差图像的低秩特性,而我们的模型考虑到对误差矩阵施加
-范数约束。同时我们对重建图像施加正则化约束旨在保持重建图像与测试图像的一致。连续系数差的平方约束旨在增强类内训练样本之间的协作。我们应用了一种ADMM算法来解决该问题。在包含遮挡和光照变化的FERET、ORL和CMU_PIE数据库上进行了大量实验证明,与回归模型相比,我们提出的模型更加鲁棒和有效。
NOTES
*通讯作者。