1. 引言
单像素成像(Single Pixel Imaging, SPI)是一种新型的成像方式,是一种典型的计算成像,能够突破传统成像中存在的物理局限。单像素成像和传统成像方式不同,传统的成像系统通常使用阵列感光传感器,其探测范围是可见光波段,超出可见光范围则探测能力迅速衰减,而使用非可见光传感器探测,其造价成本很高。单像素成像系统则与之不同,使用价格低廉的单像素探测器,如光电探测器,既能够探测更大范围的光谱,也能够对微弱光进行探测,解决了传统成像系统的部分问题,因而得到广泛的研究。
单像素成像有显著的优点,其中单像素探测器扮演了重要角色。单像素探测器具有灵敏度高,信噪比高(能够应用在极弱光 [1] 、大气湍流和散射介质成像 [2] ),时间分辨率高(能够进行飞行时间探测,实现三维计算鬼成像 [3] ),探测范围广(能够探测可见光范围外波段的光,能够实现太赫兹成像 [4] 、X射线 [5] 、红外成像 [6] 、荧光成像 [7] 等)等优势,同时单像素成像还能结合压缩感知 [8] 和深度学习的成像算法 [9] [10] [11] [12] [13] ,提高成像质量和速度。
单像素系统主要从调制方法 [14] 、采样方法 [15] - [20] 和应用 [21] - [26] 三个方向来研究。调制方式根据掩模的类型来分类,可以分为哈达玛掩模和傅里叶掩模;也能根据待成像物体的位置分为主动调制和被动调制。近些年来,单像素成像得到了快速的发展,特别是在单像素成像应用,传统图像处理中的一些方法也与单像素成像相结合,如边缘提取、空间滤波等。单像素成像不再满足“所见即所得”,对“所想即所得”有了更多的需求,需要扩展单像素成像系统的功能,然而扩展单像素成像系统功能的方法无一例外都是光路上增加器件(如低通滤波器 [27] ),或者在结构光照明(结构光探测)对掩模调制,即需要调整显示在数字阵列微镜(Digital Micromirror Devices, DMD)上的微镜来实现,如计算卷积鬼成像 [28] 将卷积过的掩模显示在DMD上,然而卷积过的掩模是个灰度图,但是DMD是二值空间光调制的器件,若要使用0和1来表示灰度值,那么就得在时间上或者在空间上取平均。这两种方法,要么导致采样时间变长,要么导致成像结果的分辨率下降。用0和1来表示灰度存在的另一个问题是在量化的过程中存在量化的误差,使得平均出来的值与实际理想的灰度值存在差值。再有就是使用平均的方法获得灰度值,灰度值介于0~1之间,当需要掩模大于1时,DMD则无能为力。
为了解决该问题,本文提出了一种基于单像素成像关联调控的方法,在重建过程中对掩模进行乘法调控,而非在DMD上对掩模调制,能够在不改变DMD上掩模的情况下,实现对物体的乘法运算,能够克服上述DMD存在的问题。而且在以往的研究中,成像过程都是遵循着“获取探测值——探测值与对应掩模关联计算”的顺序来恢复原有图像。本文提出的单像素成像的关联乘法调控技术,是通过“获取探测值——探测值与乘法调控过的掩模关联计算”的方法来重建新物体,重建结果相当于对原重建物体做了乘法运算。以往探测值与掩模一一对应关系,在某种程度上限制了单像素成像的功能性拓展。本文通过仿真和实验的方法验真了方法的有效性和先进性。本文提出的方法与先重建物体再做乘法的方法不同,本文使用的方法是边成像边做乘法调控,实现了通过对掩模做乘法实现对物体做乘法的关联调控,为未来进一步更多的关联调控奠定基础。
2. 方法及原理
单像素成像使用单像素探测器配合空间光调制器对物体进行成像,单像素成像的光路图如图1所示。

Figure 1. Configuration of single pixel imaging system
图1. 单像素成像系统光路图
首先光源的光场通过扩束镜照射在空间光调制器DMD上,空间光调制器上加载了预先设计好的掩模。光场经过空间光调制器调制后,照射在物体上,相当于和物体做点对点的乘法,然后由单像素探测器对经过聚焦透镜的光场进行探测,即对做了点对点乘法的调制光和物体每一点进行累加。将第k张掩模记为
,
;物体记为X,用向量表示
,第k张掩模和物体点对点相乘后累加的结果由单像素探测器探得,记为
。物体量化的分辨率取决于掩模的分辨率,掩模的分辨率为
,则物体的分辨率也是
,用向量表示则为
的向量;因此
可以由公式(1)表示:
(1)
上式表明,每个探测值是物体和每张掩模做内积的结果
张掩模和物体做内积得到的探测值可以由公式(2)得到,掩模向量构成的矩阵A和物体X,满足线性方程的数学模型:
(2)
其中A为观测矩阵,
,每一个横向量
都对应一张调制掩模,
,因此重建物体可以理解为解线性方程(2)。
本文提出了基于单像素成像的乘法关联调控,目的是通过对掩模做乘法调控,实现对重建物体的乘法调控。单像素成像的重建物体通过计算物体和掩模的关联性实现。要实现一次完整的单像素成像,分为两个步骤:第一个步骤是探测,第二个步骤是重建。在探测过程中,加载在DMD上的掩模和物体做点积得到探测值,DMD上加载的一系列掩模构成了观测矩阵;在重建过程中,通过对探测过程中获取的探测值和对应的掩模做关联运算,重建出物体为
满足线性方程
,
,如表1第一行所示。在探测过程中,探测值由掩模和物体共同决定,当掩模的数值扩大α倍时,观测矩阵A便扩大α倍,即
,则掩模和物体的点积(探测值)也将扩大α倍,用扩大α倍的掩模和扩大α倍的探测值做关联运算,
代表重建结果满足线性方程
,又因为
,
,因此
等价于
,故
,如表1第二行所示。当探测值为Y时,观测矩阵为
时,重建结果为
满足线性方程
,如表1第三行所示。综上分析,重建结果由探测值与重建时使用的观测矩阵共同决定。如果保持探测值不变,而改变观测矩阵,那么重建结果将也发生变化。如表1所示,探测过程和重建过程共有的仅是探测值。

Table 1. Relationship between measurement matrix, detection value and reconstruction
表1. 观测矩阵、探测值与重建结果关系
单像素乘法关联调控的方法是,在重建过程对观测矩阵做乘法调制。在不改变探测值的情况下,对所有掩模做乘法调控,调控系数记作为α,进而重建过程使用的掩模为
,
。由于控制探测值不变,即Y不变,因此新的重建结果
满足(2)的数学模型,即:
(3)
联立公式(2) (3)可以得到新的重建物体
,
。在给定的探测光强条件下,通过对重建过程的观测矩阵做乘法,新重建的结果和原来重建结果相差一个系数
,相当于对物体做了一个相关联的乘法。
3. 仿真与实验
3.1. 仿真
为了验证单像素成像乘法关联调控理论的正确性,本文先是用仿真实验进行验证。首先待成物体用一个32 × 32的矩阵来表示,十字部分的数值为0.55,其他较暗部分的值为0.25。如图2所示:
在仿真实验中使用哈达玛矩阵作观测矩阵,哈达玛矩阵的每一个行向量都对应了一张调制掩模。在仿真中,每一个调制掩模都和物体做内积运算,所得到的值即为探测值。用探测值和掩模做关联运算,使用TVAL3算法。本文提出的单像素成像的乘法关联调控,对原始的掩模做乘法调控,对每个乘法掩模乘以一个乘法调控系数α,得到新的掩模,如下图3所示:

Figure 3. New masks obtained by original masks multiplying a coefficient α
图3. 掩模乘以一个乘法调控系数α的带经过乘法调控的掩模
然后用探测值和新的掩模做关联运算,得到的结果如图4所示:

Figure 4. Reconstructions under different multiplicative coefficients α
图4. 不同乘数α的重建结果
图4表明,当乘法调控系数α的值大于1时,重建的值会随着α的增大而变暗;当α小于1时,重建的结果会随着α的减小而增强变亮。也就是说α会增强或抑制重建结果。图5取α = 1,α = 3,α = 0.4,重建的结果和待成像物体进行比较。发现当α = 1时(掩模没有做乘法调控),重建结果和待成像物体几乎完全重合;当α = 0.4时,重建的结果是黄色线条,整体扩大了差不多2.5倍;当α = 3时,重建结果为紫色线条,整体压缩了成了原来的1/3。

Figure 5. Reconstructions under different multiplicative coefficients α
图5. 不同乘法调控系数α的重建结果
把不同乘法调控系数下的重建结果记为图像矩阵Uα,U1对Uα做点对点的除法,得到结果取均值就是未进行乘法调控的重建结果与经过乘法调控的重建结果的比值,称为调控比率,记为R1/Rα。不同乘法系数与调控比率的关系如图6所示:
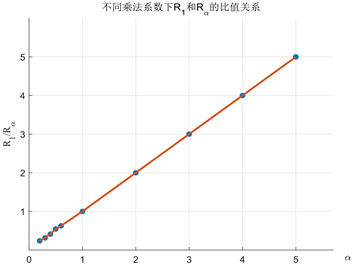
Figure 6. Relation of operation rate R1/Rα and α
图6. 调控比率R1/Rα与α的关系
如图6所示,调控比率R1/Rα和α成正比例关系,即Rα/R1与α成反比例,也就说明了当调制掩模乘以一个乘法调控系数α,新掩模和原来探测值做关联运算,重建的结果是未经乘法调控重建结果的1/α,因此实现了通过对掩模的乘法调控,间接对物体的乘法关联调控。
3.2. 实验
本文除了仿真验证,也对单像素成像乘法的关联调控进行了实验验证。光路装置图如图7所示,其中包括了光源、扩束镜、DMD、光电探测器(Photoelectric Detector, PD)、待成像物体。

Figure 7. Left figure is configuration of single pixel imaging system, the right one is the object to be imaged
图7. 左图为单像素成像系统,右图为待乘像物体
待成像物体是一个镂空的十字。在重建的过程中,使用不同的乘法系数α,得到的结果如图8所示:

Figure 8. Reconstructions under different multiplicative coefficients α
图8. 不同乘法系数α的重建结果
结果表明,不同乘法系数α调控过的掩模所重建的结果和仿真的结果一致,当α大于1时,重建结果的强度受到抑制;当α小于1时,重建结果的强度得到增强。调控系数R1/Rα和α的关系如下图9所示,其结论也和仿真的结论相同,即对调制掩模做α倍的乘法调控,新得到的掩模和探测值做关联运算,重建结果相当于做了1/α乘法调控。证明了用调控掩模的方法,能够关联地调控物体,实现间接调控的目的。
本文提出的乘法关联调控,在重建过程中使用调控过的掩模与探测值关联计算,而不用在DMD上显示灰度掩模对物体进行结构光照明(探测),每一个不同灰度的都掩模预先设计不同的掩模,然后加载在DMD上,每个灰度值需要多次探测,并多次重建,重建结果如图10。
尽管在DMD上显示不同灰度的掩模来调制光同样能实现乘法调控,但是其复杂程度远高于本文提出的乘法关联调控方法,且对环境要求更高,重建所花的时间更长,因为本文提出的方法仅需探测一次即可。而且掩模上的值无法超过1,使得乘法调控存在局限性,使得乘法结果的强度无法超过原重建物体。

Figure 9. Relation of operation rate R1/Rα and α
图9. 调控比率R1/Rα与乘法系数α的关系

Figure 10. Reconstruction results via displaying grayscale masks on DMD
图10. DMD显示不同灰度掩模的重建结果
4. 结论
本文提出了一种单像素成像系统的关联调控方式,通过对掩模进行乘法调控,从而关联地对重建物体实现乘法调控,用掩模乘以一个乘法调控系数得到新的掩模,探测值与新掩模关联计算得到的重建结果则是未经乘法调控的重建结果乘以这个调控系数的倒数。本文分别用仿真和实验的方法验证了该方法的有效性和先进性。这种关联调控方式,不需要在DMD上加载灰度掩模,而是直接在重建过程中对掩模做乘法调控,既实现了对重建物体的关联乘法调控,又避免了DMD显示灰度图时固有的精度、速度缺陷。这种调控方法不是先对物体成像后再做乘法的调控,而是对物体“边成像边调控”,同时使用了一种“探测值与调制过的掩模计算”来重建的新范式,这种重建范式打破了传统单像素成像中探测值与调制掩模一一对应的规定,能够通过在重建过程中对单像素成像系统进行功能性的拓展,为未来单像素成像的调控提供了新的思路,为除了乘法调控以外更多的调控奠定了基础。