1. 引言
湿蒸汽在发生凝结时伴随着非平衡特性,即纯净蒸汽越过饱和线由于缺乏凝结核心并不会立刻凝结,处于亚稳态状态,按照原来膨胀率继续膨胀,当达到Wilson点才会发生自发凝结,在发生凝结过程伴随着液滴成核过程与液滴生长过程,然而液滴表面张力位于成核模型的指数项,表面张力微小的变动将导致成核率发生较大的改变,近年来,研究人员用实验与数值模拟结合的方法研究湿蒸汽流动,这种方法开始受到广泛的应用 [1] [2] 。在研究时,选择合适的表面张力修正系数,对提供蒸汽凝结时的模拟精度尤为重要。
Chervko等 [3] 对表面张力进行修正,提高了数值模拟精度。Moraga等 [4] 以平面叶栅为研究对象进行非平衡凝结流动计算,当选取表面张力修正系数为0.95,模拟结果与实验更加贴合。于新峰 [5] 对一维喷管与二维平面叶栅展开数值模拟,当表面光张力修正系数为1.07能够得到较好的计算结果。姚博川等 [6] 以进口压力、温度过热度及进出口压比为变量,拟合处变量与表面张力修正系数关系,并发现四次多项式拟合效果最佳。彭姝璇等 [7] 基于拟合出表面张力修正系数的最佳取值与进口总压呈现三次方的关系。李彬等 [8] 认为在叶栅通道内发生非平衡凝结流动时,通过平面叶栅验证发现表面张力修正系数为1.13时模拟值与实验结果最贴近,韩旭等 [9] 发现表面张力修正系数与进口过热度存在一定的关系。
从已发表的资料中看,在不同的喷管或平面叶栅内,为得到更精确的模拟结果,修正系数取值不同,因此对于表面张力修正系数的取值有待商榷,本文将对该问题进行研究。
2. 控制方程
2.1. 成核模型
20世纪初Volmer、Weber等基于玻尔兹曼分布规律奠定了经典成核的理论基础,但是经典成核率未考虑两相间的传热问题,之后学者对经典成核模型进行修正,其中Kantrowitz [10] 的非等温修正模型与实验值吻合良好,其表达式如下:
(1)
式中:
为非等温修正系数;
为液滴表面张力;qc为凝结系数;ρg为气态相密度;ρl为液态相密度;m为水分子质量;Tg为气态相温度,
为临界半径。
2.2. 表面张力模型
(2)
为水平表面张力,其表达式为:
(3)
式中:Tl为液相温度,
为水的临界温度
2.3. 生长模型
(4)
式中:hgl为汽化潜热,
为蒸汽导热系数,Kn为克努森数。
2.4. 两相控制方程
质量守恒方程:
式中:
为汽相体积分数,ρg为汽相密度,uk为汽相在i方向的速度分量,Sm为源项,蒸发为正,凝结为负。
动量守恒方程:
(5)
式中:
为粘性应力张量。
对于可压缩流体,能量守恒方程采用总焓为变量,因此其能量方程:
(6)
3. 数值模拟
3.1. 喷管几何尺寸
Moore等 [11] 基于一组laval喷管(Moore喷管)研究蒸汽的凝结流动,Moore喷管有五种喷管组成通过,膨胀率范围在460 s−1 (E喷管)至3160 s−1 (A喷管),通过调整出口倾斜角与喉部宽度改变喷管的膨胀率,喷管E初始状态具有一定的湿度,但在实验过程中没有发生二次成核现象,因此本文采用A~D喷管进口为干蒸汽完成非平衡凝结流动的验证。如表1与图1为Moore喷管的几何与结构图。
3.2. 边界条件与网格无关性验证
在喷管入口布置压力和温度的探头对入口条件进行检测,沿着喷管中心线每间隔18 mm布置检测点提取沿着中心线上的静压,在距离喉部370 mm处布置光学测点测量液滴的Sauter平均直径。表2为A~D喷管实验中的边界条件。

Table 1. Moore nozzle dimensions
表1. Moore喷管尺寸

Figure 1. Schematic diagram of Moore nozzle
图1. Moore喷管示意图

Table 2. Moore nozzle boundary conditions
表2. Moore喷管边界条件
在数值计算中,湍流模型采用k-omega SST湍流模型 [12] ,壁面采用绝热无滑移壁面,网格使用结构化网格,由于在喷管喉部蒸汽参数变化梯度较大,为更好捕捉喉部与壁面处的流动现象,因此对喉部与壁面进行局部加密,网格质量均在0.9以上且y+小于5,其中c喷管的网格示意图如图2所示,对多相流动求解时打开双精度求解器,收敛标准为10−6。
网格量对整个流场分布影响较大,本文采用喷管出口流量进行网格无关性验证,图3为网格无关性验证,喷管内流量先减少后增加,网格量最后在30万稳定,为合理利用计算资源,确定网格量为30万进行计算。
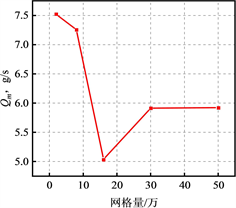
Figure 3. Grid independence verification
图3. 网格无关性验证
3.3. 表面张力修正系数的选择
由于NBTF (表面张力修正系数)位于成核率的指数项,其微小变化将引起成核数量的巨大变化,因此采用文献提供的基于进口压力与进口过热度的修正方法得到NBTF值,计算结果如表3,其中彭姝璇等 [7] 发现最佳表面张力系数的取值与进口总压呈现三次方的关系,其表达式为:
(7)
式中:p0为进口总压,单位为bar。
韩旭等 [9] 发现表面张力系数与进口过热度关系有一定相关性,其表达式如下:
(8)
式中Tin为进口过热度,单位为K。

Table 3. Calculation results of different equations
表3. 不同方程计算结果
4. 结果与分析
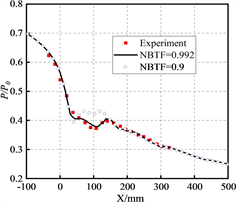
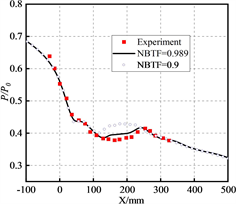
图4为Moore喷管沿中心线上的压比分布曲线,横坐标为距离喉部的距离,纵坐标为中心线上的静压与进口总压的比值,从A喷管至D喷管喉部之后扩张角减小,膨胀率减小,从图中可发现喷管内压力突升的位置逐渐远离喉部,这表明随着喷管膨胀率减小,蒸汽膨胀速率减慢,因此非平衡凝结流动产生凝结激波位置向出口移动,对上述NBTFT的数值结果与实验值基本一致,在喉部也能较好的捕捉到静压分布,具有很好的预测能力。而NBTFP在A喷管内具有很好的预测能力,但随着膨胀率的改变,数值计算结果与实验值逐渐增大,这可能是表面张力修正系数不仅与进口总压相关,也与膨胀率也由一定相关性,数值计算结果在喉部的静压高于实验值,其相关性随着膨胀率的减小逐渐降低,相比于NBTFT的结果,压力突升的位置提前发生,说明NBTFP的取值对喷管内喉部的蒸汽膨胀影响较大,由成核模型可知,随着NBTF增加,成核速率公式中的液滴表面张力增大,从而导致液滴临界半径增加,因此需要较高的过冷度来形成凝结核心,因此NBTF为0.99时压力突跃的位置落后于0.9,计算结果与实验值更加吻合。
 (a) (b)
(a) (b)
 (c) (d)
(c) (d)
Figure 4. Static pressure distribution curve. (a) Nozzle; (b) Nozzle; (c) Nozzle; (d) Nozzle
图4. 静压分布曲线。(a) 喷管;(b) 喷管;(c) 喷管;(d) 喷管
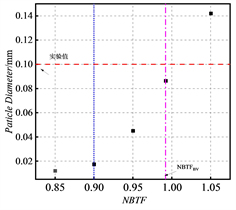
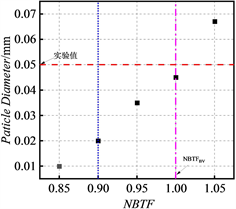
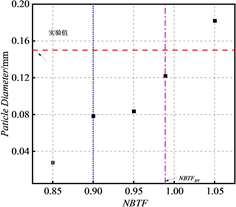
图5为在距离喉部370 mm处不同表面张力修正系数对应的液滴直径大小分布图,图中橙色为实验值蓝色和紫色对应不同回归模型计算结果,NBTFBV为最佳表面张力系数,从图中发现膨胀率可以明显影响液滴半径的大小,随着喷管膨胀率的增大,喷管内液滴直径所测量的实验值逐渐增大。不同表面张力修正系数计算的液滴直径相差较大,这是因为上述提到的表面张力在指数项对成核率影响大,进一步在液滴生长过程中产生影响,在四组喷管中,NBTFT计算结果均与实验值更加吻合,对于同一种膨胀率的喷管,随着表面张力系数的增加,液滴半径呈现增大的趋势。
为对比两中不同表面张力修正系数计算流场分布,因此采用A喷管的结果进行分析,图6为A喷管表面张力系数为1与0.9时所计算的压力云图,从图中发现收缩段,蒸汽压力不断降低,压力能逐渐转化为蒸汽动能,马赫数逐渐增大,在收缩端为亚音速流动,喉部达到音速,在喷管的扩张段做超音速流动,蒸汽参数继续降低,从图中发现两种计算结果在进口段与出口段相差不大,在喉部流场分布相差较大,这是因为在喉部蒸汽变化梯度较大。
蒸汽在膨胀过程中,压力温度逐渐降低,转变为蒸汽的动能,马赫数逐渐增加,从图7发现从喷管进口到出口马赫数逐渐增大,但在喷管的扩张段均出现马赫数减小(红框标记),这是因为湿蒸汽在凝结过程中当越过饱和线不能立刻凝结,而是以原来膨胀速率继续膨胀,这个过程过冷度逐渐增大,当达到Wilson点形成大量凝结核,蒸汽凝结释放汽化潜热对超音速气流加热,形成凝结激波,产生压力突跃,马赫数降低,对于A喷管较大的膨胀率,因此能够快速到达Wilson点,因此在喉部之后较早出现凝结激波。之后在扩张段继续膨胀,马赫数增加。
 (a) (b)
(a) (b)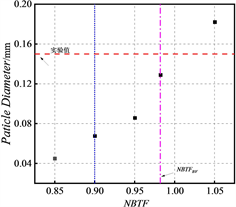
 (c) (d)
(c) (d)
Figure 5. Distribution of droplet diameter with different NBTF. (a) Nozzle; (b) Nozzle; (c) Nozzle; (d) Nozzle
图5. 液滴直径随不同NBTF分布。(a) 喷管;(b) 喷管;(c) 喷管;(d) 喷管
 (a)
(a) (b)
(b)
Figure 6. Pressure distribution cloud map. (a) The surface tension correction coefficient is 1; (b) The surface tension correction coefficient is 0.9
图6. 压力分布云图。(a) 表面张力修正系数为1;(b) 表面张力修正系数为0.9
 (a)
(a) (b)
(b)
Figure 7. Mach number distribution cloud map. (a) The surface tension correction coefficient is 1; (b) The surface tension correction coefficient is 0.9
图7. 马赫数分布云图。(a) 表面张力修正系数为1;(b) 表面张力修正系数为0.9
图8为喷管成核率分布云图。可以看出成核率在喉部附近保持较高数值,在喷管上下游,成核率基本为0。凝结核心在力学上十分稳定,但在热力学上不稳定,周围任何蒸汽参数波动都会引起水珠吸引更多的蒸汽分子聚集从而使得水珠本身不断生长,还会因为少数水珠分子质量减小变得不稳定而重新蒸发。凝结瞬间发生也是成核率发生突变的一个节点,在凝结位置前后,成核率会保持为0。表面张力修正系数为1计算的成核率最大值为1.32e22,在喷管中心段最先发生成核,壁面处延迟发生,这是因为在中心上最先达到Wilson点,壁面处受到边界层的影响,蒸汽膨胀率受到影响,表面张力修正系数为0.9计算的成核率最大值为2.721.32e23,在壁面处成核率几乎为0。
 (a)
(a) (b)
(b)
Figure 8. Nucleation rate distribution Cloud map. (a) The surface tension correction coefficient is 1; (b) The surface tension correction coefficient is 0.9
图8. 成核速率分布云图。(a) 表面张力修正系数为1;(b) 表面张力修正系数为0.9
图9为表面张力修正系数分别为0.99与0.9的湿度分布图,从图中发现在喉部之后逐渐由湿度产生,相比于表面张力修正系数为0.99表面张力修正系数为0.9最早开始出现湿度,这是因为表面张力修正系数增大,将导致临界半径增大,因此需要更高的过冷度来形成凝结核心,成核位置下移,因此湿度开始处也逐渐向下游移动。
 (a)
(a) (b)
(b)
Figure 9. Humidity distribution cloud map. (a) The surface tension correction coefficient is 1; (b) The surface tension correction coefficient is 0.9
图9. 湿度分布云图。(a) 表面张力修正系数为1;(b) 表面张力修正系数为0.9
5. 结论
1) 表面张力修正系数对喷管喉部蒸汽膨胀影响较大,采用过热度修正的数值模拟与实验值更吻合,误差最小。
2) 随着表面张力修正系数的增大,液滴半径呈增大趋势,并且取NBTFT计算结果与实验值更贴近。
3) 在云图分布中,喉部计算结果差异最大,表面张力修正系数取值大,将延迟凝结的发生。
参考文献