1. 引言
多路阀由多个电液换向阀组成,是多执行器的液压系统的核心控制元件,广泛应用于移动工程机械(如挖掘机和起重机) [1] 。在工程机械的实际应用中,由于负载压力大,执行机构流量大,工作条件变化剧烈频繁,可能会发生严重的液压冲击。而多路阀在这种工况下长时间的工作,很容易产生故障,从而影响控制精度和安全性 [2] 。多路换向阀存在多种故障,包括油液污染或阀芯频繁往复引起的磨损,以及阀门弹簧疲劳和阀芯卡死等 [3] 。其中,阀芯磨损与阀芯卡死是最常见的问题。因此,对多路阀进行故障诊断对于避免额外的液压功率损失和提高系统安全性至关重要。
根据故障诊断的理论和方法,液压系统领域常用的方法可分为两类:基于数据的诊断方法和基于模型的诊断方法 [4] 。在故障数据样本较少的情况下,基于模型的故障诊断方法是通过测量实际结果与模型预测结果的差值进行诊断决策。但是液压系统在不同的故障环境下的输出结果不同,要根据不同环境实时更新仿真模型较难,很难做到对故障的精准诊断。
深度学习是一种常用的数据驱动方法,是从信号中提取出故障的特征后进行故障分类。在液压故障诊断领域展示出强大的能力,也逐渐成为了当前的研究重点。Tang [5] 通过连续小波变换得到压力信号的时频特性后构建BO-LeNet 5模型对柱塞泵进行故障诊断。Shi [6] 从液压换向阀的多维故障信息中提取多维故障特征,在双通道CNN中加入注意力机制实现故障诊断。Ji [7] 根据对不同故障数据的敏感度选择两种基本分类器(RF、CNN),然后基于DS理论对各分类器的初始结果进行融合,得到最终换向阀的故障诊断结果。Tang [8] 构建了CNN-BO模型,从声信号的时频图像中学习有用的特征,并对液压柱塞泵的健康状态进行准确的分类。上述方法虽然有较好的故障诊断结果,但依赖于统计模型来确定系统的健康状态。当历史数据不足或操作环境突然发生变化时,这些数据可能不足以实现运行状况监测任务。
基于文献调研,我们发现:1) 基于模型的方法虽然泛化能力较低,但是可以产生大量的带有标签的故障数据。数据驱动方法虽然有很好的诊断能力,但需要大量的带有标签的故障数据作为训练,实际中的液压系统的故障数据又较难获取,因此可以考虑将两种方法的优点相结合。2) 目前液压系统领域的数据驱动方法大多基于CNN的故障诊断模型,而液压系统的原始监测数据是时间序列信号,循环神经网络(RNN)更适合处理序列数据,善于提取序列数据的整体特征,因此研究基于RNN的故障诊断模型是有必要的。
基于上述讨论,本文提出了一种基于一维卷积门控循环网络(1D-CNN + GRU)的多路阀故障诊断方法。该方法通过1D-CNN和GRU提取样本中的空间特征和时序特征,完成故障诊断。
2. 多路阀仿真模型
2.1. 多路阀工作原理
多路阀由多个工作阀片组成,采用阀前压力补偿形式,各联之间采用并联的方式,使得系统压力损失较小,达到节能的效果,其液压原理图如图1所示。
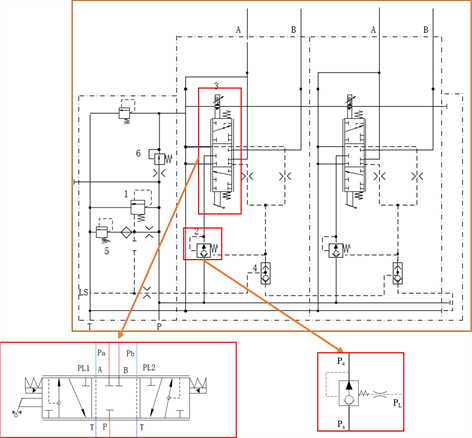
Figure 1. Hydraulic schematic diagram of the multi-way valve: (1) Safety valve; (2) Pressure compensator valve; (3) Proportional directional valve; (4) Shuttle valve; (5) Pressure relief valve; (6) Pressure reducing valve
图1. 多路阀液压原理图:(1) 安全阀;(2) 压力补偿阀;(3) 比例换向阀;(4) 梭阀;(5) 限压溢流阀;(6) 减压阀
每一联阀片主要由压力补偿阀、比例换向阀、梭阀组成。多路阀各联阀片通过负载敏感通道获取其执行机构压力的大小,最高负载压力通过梭阀反馈给单向压力补偿阀和负载敏感变量泵的负载敏感阀。通过反馈使换向阀的阀前压力与当前工作联负载压力保持不变,始终为压力补偿器的弹簧预调力。主阀输出流量保持不变,从而使执行机构的速度不会受到负载压力变化的影响。在主阀开度一定的情况下,主阀输出流量保持不变,从而使执行机构的速度不会受到负载压力变化的影响。
2.2. 多路阀数学模型推导及仿真模型建立
针对比例换向阀、压力补偿阀这些核心原件的工作原理分别建立数学模型,分述如下:
1) 主阀芯模块
根据牛顿第二定律得到主阀的阀芯运动微分方程:
(1)
其中,
是主阀右端无杆腔压力;
是主阀左端无杆腔压力;
是主阀右端无杆腔有效作用面积;
是主阀左端无杆腔有效作用面积;
是主阀弹簧刚度;
是主阀的阀芯位移;
是主阀弹簧初始拉伸量;
是主阀粘性阻尼系数;
是主阀的阀芯等效质量。
阀流量压力方程:
(2)
其中,
是流过主阀流量,
是阀芯流量系数,
是阀芯面积梯度,
是主阀前后压差,
是油液密度。
理论流量求解:
(3)
其中,
是额定压降,
是最大空载流量,即可获得理论阀系数:
(4)
假设阀芯左移为正方向
,阀芯右移为负方向
,根据公式(2),当阀芯左移
时多路阀流量方程:
(5)
当阀芯右移
时多路阀流量方程:
(6)
2) 压力补偿阀模块
根据牛顿第二定律得到压力补偿阀的阀芯运动微分方程:
(7)
其中,
是压力补偿阀右端无杆腔压力;
是压力补偿阀左端无杆腔压力;
是压力补偿阀右端无杆腔有效作用面积;
是压力补偿阀左端无杆腔有效作用面积;
是压力补偿阀弹簧刚度;
是压力补偿阀的阀芯位移;
是压力补偿阀弹簧初始拉伸量;
是压力补偿阀粘性阻尼系数;
是压力补偿阀的阀芯等效质量。
压力阀开口面积可以表达为:
(8)
其中,
是补偿阀两端压差,
是补偿阀开口面积,
是补偿阀最大开口面积,
是补偿阀调定压力,
是补偿阀压力–面积系数。
的表达式为:
(9)
其中,
是补偿阀泄漏面积,
是压力调节范围。
补偿阀两端压差在调定压力以下时:
(10)
补偿阀两端压差在最大压力以上时:
(11)
其中,
是补偿阀最大压差,其表达式为:
(12)
通过补偿阀的流量为:
(13)
2.3. 仿真模型建立
在数学模型的基础上,为方便对参数进行调整以及获取故障诊断的原始数据,在AMESim中根据多路阀数学模型和工作原理建立仿真模型,如图2所示,通过计算测试,负载敏感多路阀主要仿真调试参数如表1所示。
建立了两个工作联,每个工作联包括主阀芯、压力补偿阀以及模拟负载的比例溢流阀。负载敏感泵为两个工作阀片供油。

Table 1. Primary parameters of the multi-way valve
表1. 多路阀主要参数
3. 故障诊断模型准备
3.1. 门控循环神经网络
门控循环神经网络(GRU)由长短期记忆网络(LSTM)改进而来,二者都属于RNN的一种。GRU网络作为LSTM网络的一种变体,将LSTM中的输入门和遗忘门合成一个单一的更新门,并保留重置门,在
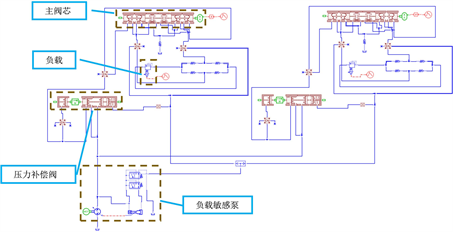
Figure 2. Multi-way valve simulation model
图2. 多路阀仿真模型
保证了预测效果的同时精简了结构,减少了训练参数。GRU的核心思想是使用两个门控单元来控制信息的流动,分别是重置门和更新门。重置门决定了前一个隐状态对当前隐状态的影响程度,更新门决定了当前隐状态对下一个隐状态的影响程度。通过这种方式,GRU可以有效地保留长期依赖的信息,并且减少了参数的数量,提高了计算效率。GRU的详细内部结构如图3所示。数学表达式为:
(14)
在t时刻,GRU的输入为
,前一时刻输入的隐藏状态为
。GRU首先计算重置门
和更新门
,然后根据
和
计算候选隐藏状态
,最后根据
、
和
计算当前隐藏状态
。其中,
、
、
——重置门、更新门和
对应的权重矩阵,
、
、
——重置门、更新门和
对应的偏置矩阵,
——sigmoid 激活函数。最后,由隐状态
来进行各单元间的信息传递。
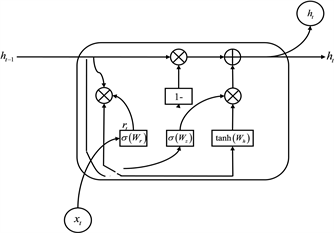
Figure 3. Diagram of the GRU network unit structure
图3. GRU网络单元结构图
3.2. 卷积神经网络
CNN拥有很好的空间特征提取能力 [9] 。在CNN中,共享权值可以有效避免算法的过拟合,而稀疏连接可以减少训练参数的数量。一维卷积神经网络(1D-CNN)常用于时间序列,其卷积输出是一维的。1D-CNN的计算细节如下所示。假设序列输入数据为
,其中d和n分别表示输入序列的维数和长度。卷积层被看作是数字滤波器的集合,它将多个局部滤波器与原始输入数据进行卷积,并生成相应的局部特征。具体的卷积运算如下所示:
(15)
设
表示滤波器向量;
表示从第i个时间步长开始的m长度的滑动窗口;
和b分别表示非线性激活函数和偏置;
表示滤波器
对相应子序列
的激活。将滤波窗口从开始时间步向结束时间步滑动,即可获得特征图。池化层的目的是减少特征映射的长度,遵循几个规则,包括平均值和最大值。
3.3. 提出的故障诊断方法
构建1D-CNN和GRU的混合神经网络的基本思想是将1D-CNN和GRU两种深度学习方法串联起来,其中1D-CNN是串联网络的初级网络,GRU是次级网络系列网络的网络。所提出的串联网络结构如图4所示,包括输入层、隐藏层和输出层。隐藏层由一个卷积层、一个池化层、一个GRU层以及一个全连接层组成,最后通过Softmax分类器对GRU输出进行分类。本文所提出的方法可识别故障的时间特性,在GRU之前使用1D-CNN作为预处理步骤来处理长时间序列,可将故障在时间顺序上进行分类。1D-CNN通过卷积层获取原始序列数据的特征。把1D-CNN特征作为GRU的输入,最终得到分类结果。
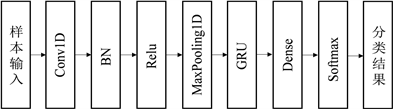
Figure 4. Diagram of the proposed cascaded network architecture
图4. 所提出的串联网络结构
4. 实验验证
4.1. 数据集说明
本文总共设置15组实验,用于获取多路阀不同的健康状态。其中主要设置了阀芯卡死和阀芯磨损两种故障,具体故障类型如表2所示,其中列出了多路阀的1种正常状态和14种故障及其对应位置以及标签。每种故障数据集包含300个样本,包含原始仿真数据以及加了4 db噪声的数据。选用50%的数据作为训练集,25%的数据作为验证集,25%的数据作为测试集。
4.2. 对比实验
为了验证所提出模型的性能,本文构建了GRU和LSTM作为对比模型。模型的具体参数设置如下:
GRU:使用1个具有8个单元的GRU层,激活函数为ReLU,采用Adam优化器更新参数,学习率设置为0.0001。

Table 2. Explanation of the health condition of the multi-way valve
表2. 多路阀健康状况说明
LSTM:使用2个具有16个单元的LSTM层,激活函数为ReLU,采用Adam优化器更新参数,学习率设置为0.0001。
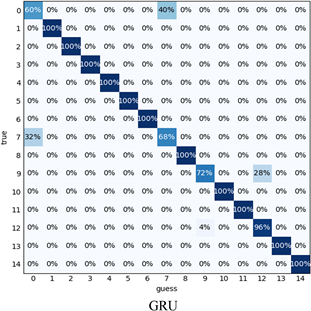
本文以准确率作为评价指标,将对比模型与1D-CNN + GRU模型进行了比较研究,预测结果如图5所示。
从表3以及图5可以看出1D-CNN + GRU相比GRU和LSTM准确率分别提升了5.86%和7.2%,具有较高的预测可靠性。相比于GRU和LSTM,本文所提出的模型将GRU与1D-CNN相结合,对多路阀中不同的特征进行区分,对关键信息给予更高的关注,有效的增加了多路阀故障诊断的精度。
 (a) 1D-CNN + GRU
(a) 1D-CNN + GRU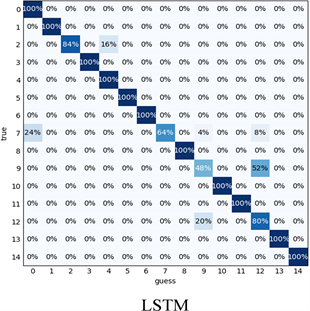
 (b) GRU (c) LSTM
(b) GRU (c) LSTM
Figure 5. Confusion matrix results of different fault diagnosis algorithms
图5. 不同故障诊断算法的混淆矩阵结果

Table 3. Accuracy rates of different algorithms
表3. 不同算法的准确率
5. 结论
本文研究液压多路阀的故障诊断,利用液压压力信号的时间序列数据进行分析。为了充分利用这些数据,采用参数较少的GRU来挖掘时间序列特征。同时,结合CNN强大的空间特征提取能力,提出了一种基于1D-CNN + GRU的多路阀故障诊断方法。首先,通过建立多路阀的AMESim仿真模型获取大量故障样本数据。然后,使用1D-CNN提取样本数据的局部特征。接下来,将每个样本的局部特征输入GRU模型,进一步提取时序特征。最后,通过Softmax分类器输出故障诊断结果。与GRU、LSTM模型相比较,实验结果表明,本文提出的1D-CNN + GRU模型具有更高的故障诊断准确率,展现出更强的故障诊断能力。