基于离散滑模控制的音圈电机伺服系统

Servo System for Voice Coil Motor Based on Discrete Sliding Mode Control

摘要: 音圈电机作为一种先进的直接驱动电机技术，已经在许多应用领域得到广泛应用，并且随着其应用场景不断扩展和发展，对于音圈电机的控制要求也在不断更新。在一些工业化场景中，受限于成本，需要在有限的计算资源里有更高效的电机控制算法，以此为设计目标，本文设计了一个改进的离散时间快速终端滑模控制算法，该算法在有外部干扰的情况下对伺服位置跟踪仍有较高精度。首先，根据数学模型推导出音圈电机的传递函数，并进一步构建出其离散状态空间方程；其次，依据滑模变结构控制理论设计离散系统控制算法，并通过数理方法验证其优越性；最后通过Simulink完成音圈电机控制系统仿真验证，仿真结果验证了该控制算法具有较高的精度，可以实现对音圈电机的精密伺服控制。

Abstract: As an advanced direct-drive motor technology, voice coil motors have been widely used in many applications, and the control requirements for voice coil motors are constantly updated as their application scenarios continue to expand and develop. In some industrialized scenarios, due to cost constraints, more efficient motor control algorithms are needed in limited computational resources, and with this as the design goal, this paper designs an improved discrete-time fast terminal sliding-mode control algorithm, which still has high accuracy for servo position tracking in the presence of external interference. Firstly, the transfer function of the voice coil motor is deduced according to the mathematical model, and its discrete state space equations are further constructed; secondly, the discrete system control algorithm is designed according to the theory of sliding mode variable structure control, and its superiority is verified by the mathematical method; finally, the control system of the voice coil motor is completed by Simulink, and the simulation result verifies that the control algorithm has a higher accuracy and can realize the precision servo control of the voice coil motor.

1. 引言

音圈电机的广泛应用对控制系统尤其控制算法具有了一定的高标准要求，随着现代智能控制算法与传感技术的发展，为音圈电机实现更高级别的超精密定位提供了可能，如PID相关控制、各类自适应控制、自抗扰与滑模控制等 [1] 。浙江理工大学的汪月生 [2] ，针对音圈电机在运行中存在的高频噪声干扰问题，提出了一种基于PID与Luenberger Observer观测器相结合的控制算法，该算法通过在电机负载增加一对反馈电阻来消除噪声，对比常规PID算法，该控制器算法不仅能够消除低频噪声，而且对高频噪声处理方面也有着明显的优势。白姗等人 [3] 针对音圈电机控制系统中存在匹配扰动和滑模抖振的问题，提出一种递归型互补滑模控制器。所提控制器在建立匹配扰动的音圈电机二阶数学模型的基础上，采用递归型设计思想，第一层为积分终端滑模，第二层为互补滑模，可以同时拥有两层滑模面的共同优点。赵家康等人 [4] 为满足振镜电机系统高精度和高动态性能的控制需求，提出了一种基于数模混合架构和扩张状态观测器–滑模控制复合的高性能驱动控制方法。仿真和实验结果表明，相比于双闭环PID控制器，所提出的高性能驱动控制方法能够有效地提升系统的鲁棒性和动态响应性能，动态响应性能提升了29.4%。

音圈电机的控制器设计十分多样，但在某些硬件资源吃紧的工业化场景中，需要有更高效的控制方法，本文以此为目标，基于现代控制理论与先进控制理论，设计一种改进的离散时间快速终端滑模控制器，相比于传统的滑模控制器，可兼顾节省计算资源与精度。

2. 音圈电机数学建模

2.1. 音圈电机的结构与原理

音圈电机采用了绕组线圈和磁场之间的相互作用来产生力和运动。它的核心部件是绕组线圈，通过在其周围通电，产生一个磁场。这个磁场与固定在外部的磁铁或永磁体产生相互作用，从而使绕组线圈受到力的作用。通过不断改变绕组线圈的电流方向和大小，音圈电机可以实现非常精确的位置控制和运动控制。音圈电机的结构示意图如图1所示 [5] 。

2.2. 音圈电机的传递函数

由基尔霍夫第二定律得到音圈电机闭合回路等效电压方程

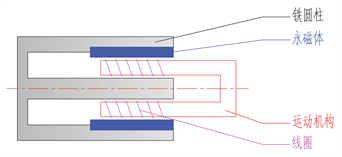
Figure 1. Voice coil motor structure schematic

图1. 音圈电机结构示意图

$U=iR+L\frac{\text{d}i}{\text{d}t}+E$ (1)

$E=K_e\frac{\text{d}x}{\text{d}t}=K_e\stackrel{\dot{}}{x}$ (2)

其中， $U$ 为音圈电机输入电压， $R$ 为线圈绕组电阻， $L$ 为线圈绕组电感， $E$ 为反电动势，由线圈在磁场中切割磁感线产生， $i$ 为线圈绕组电流， $K_e$ 为反电动势常数， $x$ 为动子位移， $\stackrel{\dot{}}{x}$ 为动子速度。

由牛顿第二定律得到音圈电机平衡方程

$F-K_{c}x=m\frac{{\text{d}}^{2}x}{\text{d}{t}^2}=\ddot{x}$ (3)

$F=K_{i}i$ (4)

其中， $F$ 为安培力， $K_c$ 为阻尼系数， $K_i$ 为力常数，单位为 $N/A$ ， $\ddot{x}$ 为动子加速度。

将式(1)-式(4)联立，进行拉氏变换得到音圈电机系统传递函数：

$\frac{X\left(s\right)}{U\left(s\right)}=\frac{K_i}{Lm{s}^3+\left(L{K}_c+Rm\right)s^2+\left(R{K}_c+K_e{K}_i\right)s}$ (5)

由于音圈电机线圈电感较小，且 $L\ll R$ ，可将其忽略得到：

$\frac{X\left(s\right)}{U\left(s\right)}=\frac{K_i}{Rm{s}^2+\left(R{K}_c+K_e{K}_i\right)s}$ (6)

2.3. 音圈电机的状态空间方程与控制目标

由音圈电机模型，设状态变量为：

$x_1=x$ ，动子的位移；

$x_2=\stackrel{\dot{}}{x}$ ，动子运动的速度。

因此音圈电机的状态方程可表示为：

$\left[\begin{array}{c}{\stackrel{\dot{}}{x}}_1\\ {\stackrel{\dot{}}{x}}_2\end{array}\right]=A_0\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+B_{0}u$ (7)

其中， $A_0=\left[\begin{array}{cc}0& 1\\ 0& -\frac{K_c}{m}\end{array}\right]$ ； $B_0=\left[\begin{array}{c}0\\ \frac{K_l{K}_a}{mR}\end{array}\right]$ 。

依据离散滑模变控制理论，将式(7)转换成离散状态方程，

$\left[\begin{array}{c}{x}_1\left(k+1\right)\\ x_2\left(k+1\right)\end{array}\right]=A_1\left[\begin{array}{c}{x}_1\left(k\right)\\ x_2\left(k\right)\end{array}\right]+B_{1}u\left(k\right)$ (8)

其中， $A_1\in {\Re }^{2\text{x}2}$ ； $B_1\in {\Re }^{2\text{x1}}$ 。

由上式得：

$\begin{array}{c}{x}_1\left(k+1\right)=x_2\left(k\right)\\ x_2\left(k+1\right)=a{x}_2\left(k\right)+bu\left(k\right)\end{array}$ (9)

式中： $a=-\frac{k_c}{m}$ ； $b=\frac{k_l{k}_a}{mR}$ 。

上式(9)为理想系统，但是音圈电机动子实际工作过程中应考虑外部扰动的干扰，得到

$\begin{array}{c}{x}_1\left(k+1\right)=x_2\left(k\right)\\ x_2\left(k+1\right)=a{x}_2\left(k\right)+bu\left(k\right)+d\left(k\right)\end{array}$ (10)

式中 $d\left(k\right)$ 可视为包括摩擦力在内的系统总扰动，并在此提出假设：

假设1：系统外部扰动总是有界的，满足 $\left|d\left(k\right)\right|\le D^{*}$ ， $D^{*}$ 为常数

考虑到控制目标是使系统位置跟踪误差趋近于零，得到：

$\begin{array}{c}{e}_1\left(t\right)=x_r\left(t\right)-x_1\left(t\right)\\ e_2\left(t\right)={\stackrel{\dot{}}{x}}_r\left(t\right)-x_2\left(t\right)\end{array}$ (11)

其中， $x_r\left(t\right)$ 为期望位置， ${\stackrel{\dot{}}{x}}_r\left(t\right)$ 为期望位置的一阶导数即期望速度。

由式(10) (11)得到跟踪误差系统方程：

$\begin{array}{c}{\stackrel{\dot{}}{e}}_1\left(t\right)=e_2\left(t\right)\\ {\stackrel{\dot{}}{e}}_2\left(t\right)=a{e}_2\left(t\right)-bu\left(t\right)+d\left(t\right)+a{\stackrel{\dot{}}{x}}_r\left(t\right)+{\ddot{x}}_r\left(t\right)\end{array}$ (12)

对式(12)离散化得到：

$\begin{array}{c}{e}_1\left(k+1\right)=e_1\left(k\right)+T_s{e}_2\left(k\right)\\ e_2\left(k+1\right)=e_2\left(k\right)+a{T}_s{e}_2\left(k\right)-b{T}_{s}u\left(k\right)\\ +T_s\left[a{\stackrel{\dot{}}{x}}_r\left(k\right)+{\ddot{x}}_r\left(k\right)\right]+T_{s}d\left(k\right)\end{array}$ (13)

3. 离散时间快速终端滑模控制器设计

在本节中将设计一种改进的离散时间快速终端滑模控制器，以提高系统输出跟踪误差的精度。在第一步中，在滑模面引入非线性项有效提高收敛速度，选择离散时间快速终端滑模面为 [6] ：

$s\left(k\right)=e_2\left(k\right)+c_1{e}_1\left(k\right)+c_{2}si{g}^{\alpha }\left(e_1\left(k\right)\right)$ (14)

其中， $si{g}^{\alpha }\left(e_1\left(k\right)\right)=\mathrm{sgn}\left(e_1\left(k\right)\right)\cdot {\left|e_1\left(k\right)\right|}^{\alpha }$ ， $0<T_s{c}_1<1$ ， $c_2>0$ ， $0<\alpha <1$ 。

基于等效控制理论，离散系统进入理想滑动模态时， $s\left(k\right)$ 满足

$s\left(k+1\right)=s\left(k\right)=0$ (15)

即

$\begin{array}{c}s\left(k+1\right)=e_2\left(k+1\right)+c_1{e}_1\left(k+1\right)+c_{2}si{g}^{\alpha }\left(e_1\left(k+1\right)\right)\\ ={\stackrel{\dot{}}{x}}_r\left(k\right)-x_2\left(k\right)+c_1\left(x_r\left(k\right)-x_1\left(k\right)\right)\\ +c_2\mathrm{sgn}\left(x_r\left(k\right)-x_1\left(k\right)\right)\cdot {\left|x_r\left(k\right)-x_1\left(k\right)\right|}^{\alpha }\\ =0\end{array}$ (16)

从而可得基于离散时间快速终端滑模控制器表达式：

$\begin{array}{c}u\left(k\right)=\frac{1}{T_{s}b}[\left(1+c_1{T}_s-T_{s}a\right)e_2\left(k\right)+c_1{e}_1\left(k\right)\\ +T_s\left[a{\stackrel{\dot{}}{x}}_r\left(k\right)+{\ddot{x}}_r\left(k\right)\right]+T_{s}d\left(k\right)+c_{2}si{g}^{\alpha }\left(e_1\left(k\right)+T_s{e}_2\left(k\right)\right)]\end{array}$ (17)

在一个控制系统中，通常会存在未建模的干扰，如摩擦力、外部扰动等。这些干扰会对系统的性能和稳定性产生负面影响。传统的控制方法往往难以准确地建模和处理这些未知干扰，为提高干扰补偿性能，引入干扰观测器 $\hat{d}\left(k\right)$ [7] ，

$\begin{array}{c}u\left(k\right)=\frac{1}{T_{s}b}[\left(1+c_1{T}_s-T_{s}a\right)e_2\left(k\right)+c_1{e}_1\left(k\right)\\ +T_s\left[a{\stackrel{\dot{}}{x}}_r\left(k\right)+{\ddot{x}}_r\left(k\right)\right]+c_{2}si{g}^{\alpha }\left(e_1\left(k\right)+T_s{e}_2\left(k\right)\right)]\\ -\hat{d}\left(k\right)\end{array}$ (18)

其中，

$\hat{d}\left(k\right)=\hat{d}\left(k-1\right)+{\left(C_s{B}_1\right)}^{-1}\delta \left[s\left(k\right)-\lambda s\left(k-1\right)+\eta \mathrm{sgn}\left(s\left(k-1\right)\right)\right]$ (19)

其中， $\lambda =1-q{T}_s>0$ ， $\eta =\epsilon T_s>0$ ， $\delta >0$ 。

基于扰动 $d\left(k\right)$ 有界，滑模面 $s\left(k\right)$ 的边界为

$\left|s\left(k\right)\right|\le \lambda =T_s\text{*}h=o\left(h\right),\forall k\in z^{+}$ (20)

由式(13)与式(14)可得跟踪误差 $e_1\left(k\right)$ 在 $k+1$ 时刻的表达式，

$\begin{array}{c}{e}_1\left(k+1\right)=e_1\left(k\right)+T_s\left[s\left(k\right)-c_1{e}_1\left(k\right)-c_{2}si{g}^{\alpha }\left(e_1\left(k\right)\right)\right]\\ =\left(1-T_s{c}_1\right)e_1\left(k\right)-T_s{c}_{2}si{g}^{\alpha }\left(e_1\left(k\right)\right)+T_{s}s\left(k\right)\end{array}$ (21)

为对上式进行分析，现引入标量动力系统，下式为标量动力系统离散化的差分方程

$w\left(k+1\right)=w\left(k\right)-l_{1}si{g}^{\alpha }\left(w\left(k\right)\right)-l_{2}w\left(k\right)+g\left(k\right)$ (22)

其中，第一项 $w\left(k\right)$ 表示当前时刻状态变量的影响，第二项 $-l_{1}si{g}^{\alpha }\left(w\left(k\right)\right)$ 表示前一时刻状态变量和输入信号的乘积产生的影响，第三项 $-l_{2}w\left(k\right)$ 表示自身状态变量的影响，第四项 $g\left(k\right)$ 表示外部干扰信号的影响， $l_1>0$ ， $1>l_2>0$ ， $1>\alpha >0$ 。

如果 $\left|g\left(k\right)\right|\le \gamma$ ， $\gamma >0$ ，则 $w\left(k\right)$ 总是有界，且存在有限个数 $K^{*}>0$ 使得

$\left|w\left(k\right)\right|\le \varphi \left(\alpha \right)\cdot \max \left\{{\left(\frac{r}{l_1}\right)}^{1/\alpha },{\left(\frac{l_1}{1-l_2}\right)}^{1/1-\alpha }\right\},\forall k\ge K^{*}$ (23)

其中， $\varphi \left(\alpha \right)$ 的表达式为：

$\varphi \left(\alpha \right)=1+{\alpha }^{\frac{\alpha }{1-\alpha }}-{\alpha }^{\frac{1}{1-\alpha }}$ (24)

$e_2\left(k\right)=s\left(k\right)-c_1{e}_1\left(k\right)-c_{2}si{g}^{\alpha }\left(e_1\left(k\right)\right)$ (25)

由引理可得， $e_1\left(k\right)$ 有界

$\begin{array}{c}\left|e_1\left(\infty \right)\right|\le \rho \\ =\varphi \left(\alpha \right)\cdot \max \left\{{\left(\frac{d*T_s{}^2}{c_2{T}_s}\right)}^{1/\alpha },{\left(\frac{c_2{T}_s}{1-c_1{T}_s}\right)}^{1/1-\alpha }\right\}\\ =\varphi \left(\alpha \right)\cdot \max \left\{\left(o{\left(h\right)}^{1/\alpha },o{\left(h\right)}^{1/1-\alpha }\right)\right\}\end{array}$ (26)

为得到更好的位置跟踪稳态误差性能指标，令式(26)中

$\frac{1}{\alpha }=\frac{1}{1-\alpha }=2$ (27)

得到

$\left|e_1\left(\infty \right)\right|\le \rho =o{\left(h\right)}^2$ (28)

若使用线性滑模面进行控制器的设计，同理可得到 $\left|e_1\left(\infty \right)\right|\le \rho =o\left(h\right)$ ，这从数理上反映了终端滑模的非线性滑模面具有更高的精度。

4. 系统仿真测试

为验证上文所设计的离散快速终端滑模控制器控制性能，现搭建一Simulink测试模型进行验证，模型主要参数如表1所示。

Table 1. System resulting data of standard experiment Simulink simulation parameter data

表1. Simulink仿真参数数据

为验证音圈电机闭环系统的动态性能，系统输入信号为全行程的10%阶跃信号，图2为阶跃响应中的位置跟踪图，图3为系统位置跟踪误差图。从图2可得上升时间为4 ms，超调量小于0.2 mm；从图3可得稳态误差小于6 × 10⁻⁶ mm。可见该系统稳定、快速、平稳且具有较小的超调，基本满足高精度的音圈电机伺服系统的工作要求。

但是在实际工作过程中，音圈电机并不是简单地做阶跃响应，更接近于正弦曲线工作响应，故为进一步验证音圈电机闭环系统动态性能，将输入信号改为振幅大小为0.6，频率为10 的正弦曲线。图4为正弦跟踪响应图，图5为正弦跟踪响应位置误差图。由图4可看出，曲线基本拟合，即实现位置跟踪，表明伺服系统在仿真中可实现对模拟工况的伺服功能，如图5所示位置跟踪误差小于2 × 10⁻⁵ mm，具有较高的精度，这样我们可以认为该闭环系统具有良好的动态性能。

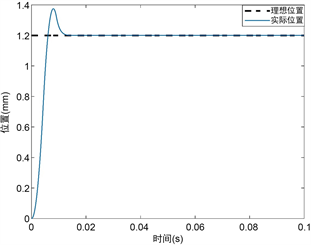
Figure 2. 10% full stroke step response

图2. 10%全行程阶跃响应

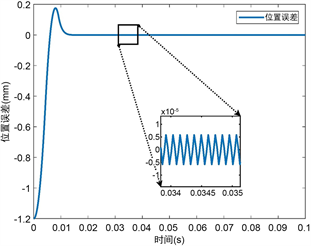
Figure 3. 10% full stroke step response position error

图3. 10%全行程阶跃响应位置误差

Figure 4. Sinusoidal tracking response

图4. 正弦跟踪响应

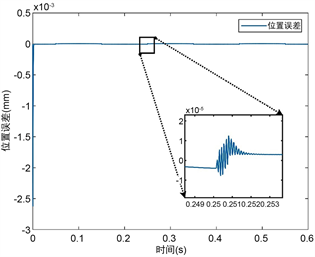
Figure 5. Sinusoidal tracking response position error

图5. 正弦跟踪响应位置误差

5. 结论

本文以音圈电机为研究对象，以实现高精度的伺服控制为目标，提出了一个改进的离散时间快速终端滑模控制算法，并在数理上验证了其精度高于传统线性滑模控制算法，并加入干扰观测器对外扰进行补偿，进一步提高了音圈电机系统的鲁棒性和稳定性，仿真测试中，系统响应迅速，稳态性能好，表明该算法在位置跟踪精度控制上有良好的表现，对音圈电机高精度伺服控制具有重要意义。