基于ANSYS的波形辐板车轮动力特性分析及结构优化

Dynamic Characteristic Analysis and Structural Optimization of Corrugated Wheel Based on ANSYS

摘要: 车轮是保证城市轨道交通车辆安全、平稳运行的最重要部件之一，其再运行中产生的机械应力、制动热应力和声辐射功率都与车轮辐板的几何形状有密切关系。其中，波形辐板车轮是国际铁路联盟UIC标准规定得标准车轮形式。波形辐板车轮辐板几何形状的优化设计可以使得用较少的材料尽可能提高轮对的承载能力和运行寿命，本设计运用SOLIDWORKS三维软件对列车车轮进行了三维建模，运用ANSYS分析了波形辐板车轮在典型工况下的应力分布状态受车轮几何形状主要参数的影响规律。通过对轨道交通车辆车轮进行有限元模拟，基于列车制造和运行中产生的应力对波形辐板车轮几何形状进行优化设计。为日后对波形辐板轮对的动力特性的研究提供了指导。

Abstract: Wheel is one of the most important components to ensure the safe and smooth operation of urban rail transit vehicles, and the mechanical stress, braking thermal stress and acoustic radiation power generated during its operation are closely related to the geometry of the wheel spoke plate. Among them, the corrugated wheel is the international railroad union UIC standard stipulates the standard wheel form. The optimized design of the spoke plate geometry of the corrugated wheel can make use of less material to improve the load carrying capacity and operating life of the wheel set as much as possible, this design uses SOLIDWORKS three-dimensional software to carry out three-dimensional modeling of the train wheel, and uses ANSYS to analyze the distribution of stress in the corrugated wheel in the typical working conditions by the influence of the main parameters of the wheel geometry law. Through the finite element simulation of the wheels of rail transit vehicles, the optimized design of the wheel geometry of the corrugated wheel is based on the stresses generated in the manufacture and operation of the train. The optimized design of the wheel geometry is based on the stresses generated during train manufacturing and operation, which provides guidance for the future research on the dynamic characteristics of corrugated wheel pairs.

1. 引言

社会生活、经济发展速度越来越依赖于铁路列车的发展。在运输行业，铁路机车要想比其他运输方式获得优势，就要提高速度、增加舒适性和安全度，经济性和环保性也需要有长足发展。我国铁路首创了速度、密度、重载并举的运输组织方式，高速和重载铁路运输向科学研究提出一系列挑战，其中车轮减重、疲劳强度和寿命就是主要问题之一 [1] [2] 。

随着列车运行速度的不断提高，轮轨系统激扰频率显著增加，轻量化轮对服役环境急剧恶化，其结构疲劳可靠性问题变得越来越突出。波形辐板车轮是国际铁路联盟UIC标准规定得标准车轮形式。波形辐板车轮辐板几何形状的优化设计可以使得用较少的材料尽可能提高轮对的承载能力和运行寿命 [3] [4] 。采用有限元分析的方法，实现在计算机虚拟环境下车轮的随机疲劳寿命预测。通过动力学仿真给出随机疲劳预测所需随机载荷谱。而结构在载荷的作用下，或者加速、减速运动时都会产生一定的弹性变形，这些变形影响了结构的运动和受力特征 [5] [6] 。

本文通过对轨道交通车辆车轮进行有限元模拟，基于列车制造和运行中产生的应力对波形辐板车轮几何形状进行优化设计。运用SOLIDWORKS三维软件对列车车轮进行了三维建模，分析波形辐板车轮在典型工况下的应力分布状态受车轮几何形状主要参数的影响规律，利用一定的优化算法，对车轮几何形状进行参数优化。最后通过遗传算法找出优化解所在范围，然后凭借振动与噪声的之间的联系，对轮辋、轮毂连接处的半径进行改进，将不同变量中的模态的固有频率与轮轨垂向力频域峰值进行比对，最终得出最优异的解，完成对结构的优化。

2. 波形辐板轮对几何模型建立

本文的研究对象是城市轨道车辆的波形辐板车轮，参考《铁路标准大全TBT4492003机车车辆车轮轮缘踏面外形》选择LM型外形车轮。在SOLIDWORKS中，根据选择好的LM型踏面和辐板绘制出三维模型。建好模型后，使用有限元分析软件ANSYS对其性能进行分析，将建立好的模型修改为通用格式并导入ANSYS软件，再根据仿真操作步骤，对模型进行材料属性设置，网格划分以及边界条件约束等设置，然后进行分析(图1)。

Figure 1. 3D model of corrugated wheel

图1. 波形辐板车轮三维模型

优质碳素结构钢60号钢为亚共析钢，强度、硬度和弹性都很高，60号钢用于制造轴、弹簧圈、轮轴、各种垫圈、凸轮、钢绳等受力较大、在摩擦条件下工作，要求较高强度、耐磨性和—定弹性的零件。因此我们选取CL60钢整体轧而成。波形辐板车轮和材料的主要参数如表1和表2所示。

Table 1. The geometric parameters of the corrugated wheel

表1. 波形辐板车轮的几何参数

Table 2. The material properties of the corrugated wheel

表2. 波形辐板车轮材料属性

3. 波形辐板轮对动力特性分析

3.1. 模态分析原理

任何体系都有固定频率和相应的振动形式，这些属于体系自身的固有属性。模态是结构的固有振动特征，因此其又被称为固有振动特征分析，用于取得结构的固有频率和振动型式，其本质是计算体系振动特征方程的特征值和特征向量。

经处理后，一个体系的振动特征可由N个微分方程表示，即：

$\left[M\right]\left\{\ddot{X}\right\}+\left[C\right]\left\{\stackrel{\dot{}}{X}\right\}+\left[K\right]\left\{X\right\}=\left\{f\left(t\right)\right\}$ (1)

式中， $f\left(t\right)$ 为N维激振向量； $\ddot{X}$ 、 $\stackrel{\dot{}}{X}$ 、 $X$ 分别为体系的位移、速度和加速度响应向量；M、K和C分别为体系的质量、刚度和阻尼矩阵，这三个矩阵一般为实对称。

设体系的初始状态为零，对上式的等式左右进行拉式变换，获得的矩阵代数方程变量为复数s，即：

$\left[M{s}^2+Cs+K\right]X\left(s\right)=F\left(s\right)$ (2)

式中矩阵叫做系统动态矩阵或广义阻抗矩阵。其逆矩阵为频率响应函数矩阵

$H\left(s\right)={\left[M{s}^2+Cs+k\right]}^{-1}$ (3)

令 $s=jw$ ，就获得了体系在频率域中输出和输入对应的关系式

$X\left(w\right)=H\left(w\right)F\left(w\right)$ (4)

$H\left(w\right)$ 矩阵中第i行和第j列的元素为:

$H_{\left(ij\right)}\left(w\right)=\frac{X_{\left(i\right)}\left(w\right)}{F_{\left(i\right)}\left(w\right)}$ (5)

等于仅在j坐标激励时，i坐标响应与激励之比。利用对称矩阵的加权正交性，有：

${\Phi }^{\text{T}}M\Phi =\left[\begin{array}{ccc}0& & \\ & m_r& \\ & & 0\end{array}\right]$ (6)

${\Phi }^{\text{T}}{\rm K}\Phi =\left[\begin{array}{ccc}0& & \\ & k_r& \\ & & 0\end{array}\right]$ (7)

因此，有：

$H\left(w\right)=\Phi \left[\begin{array}{ccc}0& & \\ & m_r& \\ & & 0\end{array}\right]{\Phi }^{\text{T}}$ (8)

N个单自由度体系频率响应的线性叠加即为N维自由度体系的频率响应。

3.2. 车轮模态分析

模态是机械结构或部件的固有振动特性，它只与结构的形状规则、材料属性、约束状态等有关，每一个模态具有特定的固有频率、阻尼比和模态振型。对车轮进行模态分析，查看其固有频率和振型，了解其振动特性，从而更好的研究车轮振动情况

对车轮进行模态分析，查看其固有频率和振型，了解其振动特性，从而更好的研究车轮振动情况。本文利用有限元软件ANSYS对车轮进行模态分析，ANSYS中模态分析方法有多种，这里我们采用Block Lanczos (分块兰索斯)法，该方法精确，计算速度快，通常用于大量模型的大量振型分析。本文计算0~2500 HZ频率范围内车轮的固有频率和振型，包含了轮轨滚动噪声的频率范围，基本能反映车轮在中低频的振动—声辐射特性。

3.2.1. 模型网格划分

将三维设计软件SOLIDWORKS中得到的模型导入ANSYS，并对模型进行网格划分。辐板的网格单元类型采用四面体单元，单元大小设置为25 mm，有限元模型包含14,741个四面体单元，27,016个节点(图2)。

Figure 2. Corrugated wheel structure meshing

图2. 波形辐板车轮网格划分

3.2.2. 约束及预应力设置

这里将车轮与车轴、车轮与轨道的关系简化，车轴与车体对车轮的作用其实际上应是有弹簧和阻尼模型，这里将车轴的约束等效成固定约束；车轮与轨道的作用其实际上存在微小弹性变形使得垂向接触力更复杂，这里将车轮与轨道简化为刚性点接触，轮轨静载荷90,000 N (图3)。

Figure 3. Corrugated wheel prestress setting

图3. 波形辐板车轮的预应力设置

3.2.3. 模态分析结果

给出了车轮在0~2500 Hz频率范围内，各阶模态的固有频率。由于车轮具有对称性结构，与圆盘具有相似的振动形式，所以车轮模态可分为面内振动的径向模态和周向模态以及面外振动的轴向模态。面外振动用节圆数m和节径数以来描述，面内振动用节径数n来描述。节圆指的是振动过程中圆盘上一个或一个以上与外形同心的圆的位移恒定为零；而节径是指振动过程中圆盘上一根或一根以上直径的位移恒定为零。

车轮的模态振型如图4所示，0节圆轴向模态踏面振动明显，若对车轮踏面施加横向激励，则轮轨接触点处横向振动明显，0节圆轴向模态主要影响曲线啸叫噪声；而l节圆轴向模态和径向模态辐板振动较大，主要影响轮轨的滚动噪声。此外，由于车轮结构的对称性，当节径数n > l时，模态成对出现，在相同频率处出现相位相差/2 pi的相同振型。

(a) (b) (c) (d) (e) (f) (g) (h) (i) (j)

Figure 4. Vibrational diagrams of the modes of the corrugated wheel. Axial modes, 0-node circle: (a) n = 0; (b) n = 1; (c) n = 2 (d) n = 3; 1-node circle: (e) n = 0; (f) n = 1. Radial modes: (g) n = 0; (h) n = 1; (i) n = 2; (j) n = 3

图4. 波形辐板车轮模态振形图。轴向模态，0节圆：(a) n = 0；(b) n = 1；(c) n = 2；(d) n = 3；1节圆：(e) n = 0；(f) n = 1。径向模态：(g) n = 0；(h) n = 1；(i) n = 2；(j) n = 3

波形辐板车轮轴向模态，0节圆，2节径的固有频率412.00 Hz、径向模态412.77 Hz；径向模态1401.0 Hz；轴向模态，1节圆1818.5 Hz。这三种情况下，为了防止发生共振，使得辐板发生变形，应避免辐板在这些频率下工作，同时应该加强辐板外表面的强度和刚度，进一步优化改进辐板的结构(表3)。

Table 3. The nature frequency of corrugated wheel

表3. 波形辐板车轮固有频率

4. 波形辐板车轮优化设计

4.1. 车轮结构优化算法

本文的车轮结构振动噪声优化属于非线性规划问题，是一个约束优化问题，且优化计算的每一次迭代均涉及离散结构的动力响应分析，计算量巨大。显然，传统的动力优化方法，如数学规划法和优化准则法，求解这类问题具有很大局限性。因为传统优化方法大都属于基于梯度的局部优化方法，需要针对特定问题进行繁琐的动力灵敏度分析，通用性和易用性差，而且容易陷入局部极值点，难以有效搜索不连通或非凸的复杂可行域。遗传算法是一类基于自然选择和群体遗传学机理上的自适应概率搜索的全局优化方法，它不需要梯度信息指导搜索方向，只是以目标函数值作为搜索信息，为求解复杂优化问题提供了一个通用框架，很适合于本文所提出的优化问题。但是，遗传算法不能直接计算有约束的优化问题，必须将有约束的优化问题转化为无约束优化问题进行求解。由于本文所提出的优化问题约束形式为区域约束，因此可以通过特殊的编码把有约束的优化问题转化为无约束问题。

本文中，r1，r2和r3属于区间[60, 70]，将这个区间都划分为2个等分，每个等分的长度 = 5编码的对应关系如下：

00 = 0 → 60

01 = 1→ 65

10 = 2→ 70

3个变量r1，r2和r3组成一组2位二进制整数，构成一个个体的基因型。上述编码方法保证了搜索空间中一个个体的点与解空间内一个可行解的点有一一对应的关系，同时也保证了经过交叉、变异等遗传算子作用之后产生的新个体在解空间中也有确定的对应解，而不会产生超出约束区间的无效解。采用这种处理方法的另一个原因是在遗传算法中设置最小搜索空间，能够提高遗传算法的搜索效率。

按照上述算法，对于任意一组给定的设计变量，使用ANSYS软件进行模态分析和响应分析，得到车轮所选节点的位移、应力等，计算目标函数和优良度。根据计算结果，用遗传算法对设计变量进行优化并给出下一代群体参数。

4.2. 优化变量

铁道车辆车轮轮辋和踏面的轮廓以及轮毂的设计参数都是按相关的国家标准和铁路行业标准执行的，因此并不是所有车轮的设计参数都可以供设计人员进行修改的。另外，轮对的内侧距与轨距决定了轮辋相对于轮毂位置的偏移尺寸，而轮毂直径取决于车轴直径，也是预先确定的。因此，能够进行参数改进设计的只有车轮辐板位置、辐板角度、辐板与轮辋、轮毂连接处的半径。为了保证优化设计后的车轮断面不会偏离原设计太远，本文选取辐板与轮辋、轮毂连接处的内外侧半径作为设计变量。如图5所示。

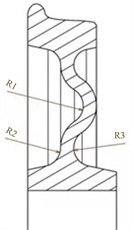
Figure 5. Schematic diagram of optimization variables

图5. 优化变量示意图

4.3. 优化结果分析

这里我们采用Block Lanczos (分块兰索斯)法，将得到的各个不同变量中的模态中的固有频率与轮轨垂向力频域峰值处 [7] 进行对比。通过找出其中和其值相差最大的一个，以此来避免共振，然后在其中选出频率最低的以此来降低噪声的影响，从而得出最优解。通过改变变量，得到了以下的结果(图6)。

(a) (b) (c) (d) (e) (f)

Figure 6. Corrugated wheel prestress setting. (a)~(b) R = 60, 60, 60；(c)~(d) R = 65, 65, 65; (e)~(f) R = 70, 70, 70

图6. 不同变量的模态振形图。(a)~(b) R = 60，60，60；(c)~(d) R = 65，65，65；(e)~(f) R = 70，70，70

通过ANSYS对于多个变量的分析并与轮轨垂向力比较分析得出：在初始状态的波形辐板车轮轴向模态，0节圆，2节径的固有频率412.00 Hz、径向模态412.77 Hz与轮对轮轨垂向力频域峰值处395.5 Hz比较相近；径向模态1401.0 Hz和轮对轮轨垂向力频域峰值处1406 Hz比较相近；轴向模态，1节圆1818.5 Hz和轮对轮轨垂向力频域峰值处1792 Hz比较相近。进过多个比对与分析，发现三个变量分别是70, 70, 70的时候，与轮轨垂向力的固有频率差异最大，不易发起共振的同时，频率最小，所造成噪声声辐射最小。此外，70, 70, 70尺寸的车轮在受载荷下的等效应力分布更均匀，虽然其幅板中部和轮毂连接处的应力与60, 60, 60相比之下更大，但是质量上前者轻了9.0 kg，而且在几何形状上更利于铸造出模。在疲劳强度下，70, 70, 70尺寸的车轮幅板应力幅值更低，分布更集中，各点的应力发散程度小。在热应力分析下，计算出的结果同样是70, 70, 70尺寸车轮的等效热应力更低。最后通过遗传算法找出了与轮对轮轨垂向力频域峰值处有着明显差异的解，在以防止共振的前提下，进过多个比对与分析，发现三个变量分别是70, 70, 70的时候，与轮轨垂向力的频域峰值差异最大，不易发起共振的同时，频率最小，所造成噪声声辐射最小，完成优化。所以最后得出当r1 = 70, r2 = 70, r3 = 70时是最优解。

5. 结论

为了解决波形辐板车轮在典型工况下应力分布状态，并提高其性能。本文利用SOLIDWORKS三维软件对列车车轮进行三维建模，通过分析波形辐板车轮在典型工况下由于主要车轮几何参数的影响而产生的应力分布状态，并利用一定的算法对车轮几何参数进行优化，研究了铁路车辆车轮的结构、工作原理和设计方法。最后，利用遗传算法求出优化解，再根据振动-噪声耦合的强度、轮辋、轮毂连接半径等确定解的峰值，对于垂直力在频域上有明显差异的车轮和钢轨进行优化，以避免共振、基于假设进行多次对比分析，发现三个变量分别为70, 70 ,70，且车轮和钢轨的垂直力内频相差最大，不易同时引发共振，最低频率导致噪声发射最小，充分优化。