高精度积分值四次B样条拟插值

High Accuracy Integro Quartic B-Spline Quasi-Interpolation

摘要: 目的：在函数重构问题中，节点处的函数值是未知的，而连续区间上的积分值是已知的。如何利用连续区间上积分值信息来解决函数重构是一个重要的问题。本文给出一种高精度积分值四次B样条拟插值算子解决连续区间上积分值的函数重构问题。方法：首先利用连续区间上的积分值的线性组合构造新的泛函系数，即结点处的函数值和一阶导数值的逼近值，进而基于带导数信息的高精度B样条拟插值算子，得到高精度积分值四次B样条拟插值。最后给出该算子对函数及其高阶导数的逼近误差。结果：在数值实例中，从逼近误差、数值收敛阶等方面验证了该方法的有效性。结论：本文构造的算子不依赖于目标函数导数信息，不需额外边界信息，不需求解方程组并且次数为四次，计算更为简便。与已有成果相比较，对函数及其高阶导数的逼近精度更高。

Abstract: Objective: In the function reconstruction problem, the function values at the knots are unknown, and the integral values on the successive subintervals are known. How to use the integral values information on the successive subintervals to solve the function reconstruction is an important problem. In this paper, the high accuracy integro quartic B-spline quasi-interpolation operator given in this paper effectively solves the problem of function reconstruction of integral values on successive subintervals. Method: Firstly, a new functional coefficient is constructed by using the linear combination of the integral values on the successive subintervals, that is, the function values at the knots and the approximation value of the first-order derivative. Then, based on the high accuracy B-spline quasi-interpolation operator with derivative information, the high accuracy integro quartic B-spline quasi-interpolation is obtained. Finally, the approximation error of the operator to the function and its higher order derivatives is given. Result: In numerical examples, the effectiveness of the method is verified from the aspects of approximation error and numerical convergence order. Conclusion: The operator constructed in this paper does not depend on the derivative information of the objective function, does not need additional boundary information, does not need to solve the equations, and the number of times is four, and the calculation is simpler. Compared with the existing results, the approximation accuracy of the function and its higher order derivatives is higher.

1. 引言

在许多的实际问题中，我们会遇到这样的问题：函数未知，同时也不知道函数在离散点处的函数值，但是已知它在连续等距区间上的积分值，如何利用已知的积分值信息来重构原函数及其导函数呢？此类问题经常出现在力学、电气、数理统计、插值与逼近、环境科学、气候学、海洋学等研究领域 [1] [2] [3] [4] ，因此具有重要的理论和应用研究价值，在过去的十几年里引起了广泛的关注。

样条函数作为具有一定光滑度的分段多项式具有较好的数值稳定性和收敛性等优点，可以被用来处理此类问题. 2006年，Behforooz [5] 首次提出利用连续等距区间上的积分值来构造三次样条函数，在构造过程中运用了Hermite插值多项式和3个额外的边界条件。Behforooz [6] 使用 [5] 中相同的方法构造了积分值五次样条插值。不过，这些方法都需要相对复杂的推导过程以及额外的边界条件，并且这些方法不能逼近高阶导数。2010年，Zhanlav和Mijiddorj [7] 在不需要额外条件情况下，利用三次B样条解决了局部积分值样条插值问题并给出了对高阶导数的逼近性质。2012年，Lang和Xu [8] 在同样不需要边界条件的情况下，使用四次B样条进行积分值样条插值，并且证明出了该方法在逼近节点处的函数值和二阶导数值时具有超收敛性。2013年，Wu和Zhang [9] 等利用类似的方法讨论了积分值六次样条插值，并且证明了该方法在逼近节点处的函数值、节点处的二阶导数值和四阶导数值时具有超收敛性。2015年，Wu和Zhang [10] 讨论了任意连续子区间上的积分值二次样条插值。以上这些方法都需要求解线性方程组，计算过程比较复杂。2015年，Boujraf [11] 给出了一种简单的方法去构造积分值三次样条拟插值算子，此构造方法不需要额外的边界条件，并且不需要解线性方程组。其主要思想就是用积分值的线性组合逼近函数值，再将其代入三次样条拟插值算子中，得到积分值三次样条拟插值。2017年，吴金明等 [12] 提出了一种基于未知函数在连续等距区间上的积分值和多层样条拟插值技术来解决函数重构问题，该方法较之于已有的积分值三次样条拟插值方法具有更好的逼近误差和数值收敛阶。2018年，吴金明等 [13] 利用文献 [11] 的方法，构造了积分值五次样条拟插值。

样条拟插值有很多好的性质，比如局部性、计算复杂度低、良好的保形性、多项式再生性等，2005年，Sablonniere [14] 构造了一元二次、三次、四次、五次B样条拟插值算子，并应用于数值微分和数值积分。Zhang S等 [15] 在一元三次B样条拟插值算子的基础上，构造了一种带有导数信息的高精度四次B样条拟插值算子，该算子能够再生更高次多项式并且误差精度更高。

本文利用连续区间上的积分值的线性组合构造新的泛函系数，包括结点处的函数值和一阶导数值，结合四次拟插值算子构造高精度积分值四次拟插值算子，为了提高精度，现有的拟插值算子大都需要目标函数的导数信息，而这些信息在实际问题中难以得到。本文构造的算子不依赖于目标函数导数信息，避免了这一问题。不需额外边界信息，不需求解方程组并且次数为四次，计算更为简便。通过数值实例可以看出，与已有成果相比较，对函数及其高阶导数的逼近精度更高。

2. 高精度B样条拟插值

本节介绍高精度B样条拟插值算子 [15]

${\tilde{Q}}_{3,1}f\left(x\right)={\displaystyle \underset{i=0}{\overset{n}{\sum }}\left[f_i+\frac{1}{4}{f^{\prime }}_i\left(x-x_i\right)\right]H_i\left(x\right)}$ (1)

其中 $\left\{\left(x_i,f_i,{f^{\prime }}_i\right)\right\}$ 为数据点， $x_i=a+ih$ ， $h:=\frac{b-a}{n}$ ， $n\ge 8$ ， $f_i$ 表示 $f\left(x\right)$ 在 $x_i$ 点处的离散值 $f\left(x_i\right)$ ， ${f^{\prime }}_i$ 表示 $f\left(x\right)$ 在 $x_i$ 点处的一阶导数值 $f^{\prime }\left(x_i\right)$ 。

$H_i\left(x\right)$ 由基函数组 $B_i$ 线性表示：

$\begin{array}{l}{H}_0:=B_1+\frac{7}{18}{B}_2-\frac{1}{6}{B}_3,\\ H_1:=B_2+\frac{8}{6}{B}_3-\frac{1}{6}{B}_4,\\ H_2:=-\frac{1}{2}{B}_2-\frac{1}{6}{B}_3+\frac{8}{6}{B}_4-\frac{1}{6}{B}_5,\\ H_3:=\frac{1}{9}{B}_2-\frac{1}{6}{B}_4+\frac{8}{6}{B}_5-\frac{1}{6}{B}_6,\\ H_i:=-\frac{1}{6}{B}_{i+1}+\frac{8}{6}{B}_{i+2}-\frac{1}{6}{B}_{i+3},i=4,5,\cdots ,n-4,\end{array}$

$\begin{array}{l}{H}_{n-3}:=\frac{1}{9}{B}_{n+2}-\frac{1}{6}{B}_n+\frac{8}{6}{B}_{n-1}-\frac{1}{6}{B}_{n-2},\\ H_{n-2}:=-\frac{1}{2}{B}_{n+2}-\frac{1}{6}{B}_{n+1}+\frac{8}{6}{B}_n-\frac{1}{6}{B}_{n-1},\\ H_{n-1}:=B_{n+2}+\frac{8}{6}{B}_{n+1}-\frac{1}{6}{B}_n,\\ H_n:=B_{n+3}+\frac{7}{18}{B}_{n+2}-\frac{1}{6}{B}_{n+1},\end{array}$

其中 $\left\{B_i,i=1,2,\cdots ,n+3\right\}$ 是定义在准均匀节点向量 $X_n:=\left\{x_i,-3\le i\le n+3\right\}$ 和重节点 $x_{-3}=x_{-2}=x_{-1}=a,x_{n+1}=x_{n+2}=x_{n+3}=b$ 上的3次B样条基函数。

拟插值算子 ${\tilde{Q}}_{3,1}f\left(x\right)$ 误差逼近阶是5，有如下定理：

定理1 [15] 已知函数 $f\in C^5\left[a,b\right]$ ，如果 $x\in \left[a,b\right]$ ，则有

$\left|f\left(x\right)-{\tilde{Q}}_{3,1}f\left(x\right)\right|\le BK{h}^5$

其中 $K=\underset{a\le \xi \le b}{\max }\left|f^{\left(5\right)}\left(\xi \right)\right|$ .B为正常数，在不同区间取值不同，具体地，

1) 如果 $x\in \left[x_2,x_{n-2}\right)$ ， $B=\frac{401}{8640}\approx 0.0464$

2) 如果 $x\in \left[x_0,x_1\right)\cup \left[x_{n-1},x_n\right]$ ， $B=\frac{1}{480}\left(-\frac{283}{27}+9\sqrt{3}+\frac{231\sqrt{7}}{27}\right)\approx 0.0578$

3) 如果 $x\in \left[x_1,x_2\right)\cup \left[x_{n-2},x_{n-1}\right]$ ， $B=\frac{1}{480}\left(\frac{23717}{1764}+\frac{61\sqrt{35}}{441}\right)\approx 0.0297$

3. 构造高精度积分值B样条拟插值

设 $f\left(x\right)$ 是 $\left[a,b\right]$ 上一个未知函数，利用n + 1个节点将区间 $\left[a,b\right]$ 进行均匀分割

$a=x_0<x_1<\cdots <x_{n-1}<x_n=b$

其中， $x_i=a+ih$ ， $i=0,1,\cdots ,n$ ， $h=\frac{b-a}{n}$ 。

已知函数 $f\left(x\right)$ 在n个子区间 $\left[x_i,x_{i+1}\right]$ 上的积分值 $I_i$ ，即

$I_i={\displaystyle {\int }_{x_i}^{x_{i+1}}f\left(x\right)\text{d}x},i=0,1,\cdots ,n-1$ (2)

本文要解决的问题就是利用已知函数在连续等距区间上积分值的信息来解决函数重构问题。

3.1. 函数值与一阶导数值的逼近

本文利用连续区间上的积分值的线性组合得到结点处函数值的六阶逼近，一阶导数值的五阶逼近。

定理1对于 $i=3,4,\cdots ,n-3$ 有

${\tilde{f}}_i=\frac{1}{60h}\left(I_{i-3}-8I_{i-2}+37I_{i-1}+37I_i-8I_{i+1}+I_{i+2}\right)=f_i+O\left(h^6\right)$ (3)

${{\tilde{f}}^{\prime }}_i=\frac{1}{180h^2}\left(-2I_{i-3}+25I_{i-2}-245I_{i-1}+245I_i-25I_{i+1}+2I_{i+2}\right)={f^{\prime }}_i+O\left(h^5\right)$ (4)

证明：当 $i=3,4,\cdots ,n-3$ 时，将 $f\left(x\right)$ 在 $x_i$ 处展开如下：

$f\left(x\right)={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{f_i^{\left(j\right)}}{j!}}{\left(x-x_i\right)}^j$

$\begin{array}{c}{I}_i={\displaystyle {\int }_{x_i}^{x_{i+1}}f\left(x\right)\text{d}x}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{f_i^{\left(j\right)}}{j!}{\displaystyle {\int }_{x_i}^{x_{i+1}}{\left(x-x_i\right)}^j\text{d}x}}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{h^{j+1}}{\left(j+1\right)!}{f}_i^{\left(j\right)}}\\ =f_{i}h+\frac{{f^{\prime }}_i}{2!}{h}^2+\frac{{f^{″}}_i}{3!}{h}^3+\frac{{f^{‴}}_i}{4!}{h}^4+\frac{f_i{}^{\left(4\right)}}{5!}{h}^5+\frac{f_i{}^{\left(5\right)}}{6!}{h}^6+O(\; h\; 7\; )\end{array}$

同理可得

$\begin{array}{c}{I}_{i-1}={\displaystyle {\int }_{x_{i-1}}^{x_i}f\left(x\right)\text{d}x}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{f_i^{\left(j\right)}}{j!}{\displaystyle {\int }_{x_{i-1}}^{x_i}{\left(x-x_i\right)}^j\text{d}x}}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\left(-1\right)}^j\frac{h^{j+1}}{\left(j+1\right)!}{f}_i^{\left(j\right)}}\\ =f_{i}h-\frac{{f^{\prime }}_i}{2!}{h}^2+\frac{{f^{″}}_i}{3!}{h}^3-\frac{{f^{‴}}_i}{4!}{h}^4+\frac{f_i{}^{\left(4\right)}}{5!}{h}^5-\frac{f_i{}^{\left(5\right)}}{6!}{h}^6+O(\; h\; 7\; )\end{array}$

$\begin{array}{c}{I}_i+I_{i+1}={\displaystyle {\int }_{x_i}^{x_{i+2}}f\left(x\right)\text{d}x}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{f_i^{\left(j\right)}}{j!}{\displaystyle {\int }_{x_i}^{x_{i+2}}{\left(x-x_i\right)}^j}}\text{d}x={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{{\left(2h\right)}^{j+1}}{\left(j+1\right)!}{f}_i^{\left(j\right)}}\\ =f_i\left(2h\right)+\frac{{f^{\prime }}_i}{2!}{\left(2h\right)}^2+\frac{{f^{″}}_i}{3!}{\left(2h\right)}^3+\frac{{f^{‴}}_i}{4!}{\left(2h\right)}^4+\frac{f_i{}^{\left(4\right)}}{5!}{\left(2h\right)}^5+\frac{f_i{}^{\left(5\right)}}{6!}{\left(2h\right)}^6+O(\; h\; 7\; )\end{array}$

$\begin{array}{c}{I}_{i-2}+I_{i-1}={\displaystyle {\int }_{x_{i-2}}^{x_i}f\left(x\right)\text{d}x}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{f_i^{\left(j\right)}}{j!}{\displaystyle {\int }_{x_{i-2}}^{x_i}{\left(x-x_i\right)}^j}}\text{d}x={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\left(-1\right)}^j\frac{{\left(2h\right)}^{j+1}}{\left(j+1\right)!}{f}_i^{\left(j\right)}}\\ =f_i\left(2h\right)-\frac{{f^{\prime }}_i}{2!}{\left(2h\right)}^2+\frac{{f^{″}}_i}{3!}{\left(2h\right)}^3-\frac{{f^{‴}}_i}{4!}{\left(2h\right)}^4+\frac{f_i{}^{\left(4\right)}}{5!}{\left(2h\right)}^5-\frac{f_i{}^{\left(5\right)}}{6!}{\left(2h\right)}^6+O(\; h\; 7\; )\end{array}$

$\begin{array}{c}{I}_i+I_{i+1}+I_{i+2}={\displaystyle {\int }_{x_i}^{x_{i+3}}f\left(x\right)\text{d}x}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{f_i^{\left(j\right)}}{j!}{\displaystyle {\int }_{x_i}^{x_{i+3}}{\left(x-x_i\right)}^j}}\text{d}x={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{{\left(3h\right)}^{j+1}}{\left(j+1\right)!}{f}_i^{\left(j\right)}}\\ =f_i\left(3h\right)+\frac{{f^{\prime }}_i}{2!}{\left(3h\right)}^2+\frac{{f^{″}}_i}{3!}{\left(3h\right)}^3+\frac{{f^{‴}}_i}{4!}{\left(3h\right)}^4+\frac{f_i{}^{\left(4\right)}}{5!}{\left(3h\right)}^5+\frac{f_i{}^{\left(5\right)}}{6!}{\left(3h\right)}^6+O(\; h\; 7\; )\end{array}$

$\begin{array}{c}{I}_{i-3}+I_{i-2}+I_{i-1}={\displaystyle {\int }_{x_{i-3}}^{x_i}f\left(x\right)\text{d}x}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{f_i^{\left(j\right)}}{j!}{\displaystyle {\int }_{x_{i-3}}^{x_i}{\left(x-x_i\right)}^j}}\text{d}x={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\left(-1\right)}^j\frac{{\left(3h\right)}^{j+1}}{(j+1)!}{f}_i^{\left(j\right)}}\\ =f_i\left(3h\right)-\frac{{f^{\prime }}_i}{2!}{\left(3h\right)}^2+\frac{{f^{″}}_i}{3!}{\left(3h\right)}^3-\frac{{f^{‴}}_i}{4!}{\left(3h\right)}^4+\frac{f_i{}^{\left(4\right)}}{5!}{\left(3h\right)}^5-\frac{f_i{}^{\left(5\right)}}{6!}{\left(3h\right)}^6+O(\; h\; 7\; )\end{array}$

由上，得到线性方程组

$\{\begin{array}{l}{f}_{i}h+\frac{{f^{\prime }}_i}{2!}{h}^2+\frac{{f^{″}}_i}{3!}{h}^3+\frac{{f^{‴}}_i}{4!}{h}^4+\frac{f_i{}^{\left(4\right)}}{5!}{h}^5+\frac{f_i{}^{\left(5\right)}}{6!}{h}^6+O\left(h^7\right)=I_i\\ f_{i}h-\frac{{f^{\prime }}_i}{2!}{h}^2+\frac{{f^{″}}_i}{3!}{h}^3-\frac{{f^{‴}}_i}{4!}{h}^4+\frac{f_i{}^{\left(4\right)}}{5!}{h}^5-\frac{f_i{}^{\left(5\right)}}{6!}{h}^6+O\left(h^7\right)=I_{i-1}\\ f_i\left(2h\right)+\frac{{f^{\prime }}_i}{2!}{\left(2h\right)}^2+\frac{{f^{″}}_i}{3!}{\left(2h\right)}^3+\frac{{f^{‴}}_i}{4!}{\left(2h\right)}^4+\frac{f_i{}^{\left(4\right)}}{5!}{\left(2h\right)}^5+\frac{f_i{}^{\left(5\right)}}{6!}{\left(2h\right)}^6+O\left(h^7\right)=I_i+I_{i+1}\\ f_i\left(2h\right)-\frac{{f^{\prime }}_i}{2!}{\left(2h\right)}^2+\frac{{f^{″}}_i}{3!}{\left(2h\right)}^3-\frac{{f^{‴}}_i}{4!}{\left(2h\right)}^4+\frac{f_i{}^{\left(4\right)}}{5!}{\left(2h\right)}^5-\frac{f_i{}^{\left(5\right)}}{6!}{\left(2h\right)}^6+O\left(h^7\right)=I_{i-2}+I_{i-1}\\ f_i\left(3h\right)+\frac{{f^{\prime }}_i}{2!}{\left(3h\right)}^2+\frac{{f^{″}}_i}{3!}{\left(3h\right)}^3+\frac{{f^{‴}}_i}{4!}{\left(3h\right)}^4+\frac{f_i{}^{\left(4\right)}}{5!}{\left(3h\right)}^5+\frac{f_i{}^{\left(5\right)}}{6!}{\left(3h\right)}^6+O\left(h^7\right)=I_i+I_{i+1}+I_{i+2}\\ f_i\left(3h\right)-\frac{{f^{\prime }}_i}{2!}{\left(3h\right)}^2+\frac{{f^{″}}_i}{3!}{\left(3h\right)}^3-\frac{{f^{‴}}_i}{4!}{\left(3h\right)}^4+\frac{f_i{}^{\left(4\right)}}{5!}{\left(3h\right)}^5-\frac{f_i{}^{\left(5\right)}}{6!}{\left(3h\right)}^6+O\left(h^7\right)=I_{i-3}+I_{i-2}+I_{i-1}\end{array}$

整理得

$\left(\begin{array}{cccccc}1& 1& 1& 1& 1& 1\\ 1& -1& 1& -1& 1& -1\\ 2& 2^2& 2^3& 2^4& 2^5& 2^6\\ 2& -2^2& 2^3& -2^4& 2^5& -2^6\\ 3& 3^2& 3^3& 3^4& 3^5& 3^6\\ 3& -3^2& 3^3& -3^4& 3^5& -3^6\end{array}\right)\left(\begin{array}{c}{f}_{i}h+O\left(h^7\right)\\ \frac{{f^{\prime }}_i}{2!}{h}^2+O\left(h^7\right)\\ \frac{{f^{″}}_i}{3!}{h}^3+O\left(h^7\right)\\ \frac{{f^{‴}}_i}{4!}{h}^4+O\left(h^7\right)\\ \frac{f_i{}^{\left(4\right)}}{5!}{h}^5+O\left(h^7\right)\\ \frac{f_i{}^{\left(5\right)}}{6!}{h}^6+O\left(h^7\right)\end{array}\right)=\left(\begin{array}{c}{I}_i\\ I_{i\text{-1}}\\ I_i+I_{i+1}\\ I_{i-2}+I_{i-1}\\ I_i+I_{i+1}+I_{i+2}\\ I_{i-3}+I_{i-2}+I_{i-1}\end{array}\right)$

$\left(\begin{array}{c}{f}_{i}h+O\left(h^7\right)\\ \frac{{f^{\prime }}_i}{2!}{h}^2+O\left(h^7\right)\\ \frac{{f^{″}}_i}{3!}{h}^3+O\left(h^7\right)\\ \frac{{f^{‴}}_i}{4!}{h}^4+O\left(h^7\right)\\ \frac{f_i{}^{\left(4\right)}}{5!}{h}^5+O\left(h^7\right)\\ \frac{f_i{}^{\left(5\right)}}{6!}{h}^6+O\left(h^7\right)\end{array}\right)=\left(\begin{array}{cccccc}\frac{3}{4}& \frac{3}{4}& -\frac{3}{20}& -\frac{3}{20}& \frac{1}{60}& \frac{1}{60}\\ \frac{3}{4}& -\frac{3}{4}& -\frac{3}{40}& \frac{3}{40}& \frac{1}{180}& -\frac{1}{180}\\ -\frac{13}{48}& -\frac{13}{48}& \frac{1}{6}& \frac{1}{6}& -\frac{1}{48}& -\frac{1}{48}\\ -\frac{13}{48}& \frac{13}{48}& \frac{1}{12}& -\frac{1}{12}& -\frac{1}{144}& \frac{1}{144}\\ \frac{1}{48}& \frac{1}{48}& -\frac{1}{60}& -\frac{1}{60}& \frac{1}{240}& \frac{1}{240}\\ \frac{1}{48}& -\frac{1}{48}& -\frac{1}{120}& \frac{1}{120}& \frac{1}{720}& -\frac{1}{720}\end{array}\right)\left(\begin{array}{c}{I}_i\\ I_{i-1}\\ I_i+I_{i+1}\\ I_{i-2}+I_{i-1}\\ I_i+I_{i+1}+I_{i+2}\\ I_{i-3}+I_{i-2}+I_{i-1}\end{array}\right)$

则有

$\begin{array}{l}{f}_{i}h+O\left(h^7\right)=\frac{1}{60}{I}_{i-3}-\frac{2}{15}{I}_{i-2}+\frac{37}{60}{I}_{i-1}+\frac{37}{60}{I}_i-\frac{2}{15}{I}_{i+1}+\frac{1}{60}{I}_{i+2}\\ \frac{{f^{\prime }}_i}{2!}{h}^2+O\left(h^7\right)=-\frac{1}{180}{I}_{i-3}+\frac{5}{72}{I}_{i-2}-\frac{49}{72}{I}_{i-1}+\frac{49}{72}{I}_i-\frac{5}{72}{I}_{i+1}+\frac{1}{180}{I}_{i+2}\end{array}$

即得

$\begin{array}{l}{\tilde{f}}_i=\frac{1}{60h}\left(I_{i-3}-8I_{i-2}+37I_{i-1}+37I_i-8I_{i+1}+I_{i+2}\right)=f_i+O\left(h^6\right)\\ {{\tilde{f}}^{\prime }}_i=\frac{1}{180h^2}\left(-2I_{i-3}+25I_{i-2}-245I_{i-1}+245I_i-25I_{i+1}+2I_{i+2}\right)={f^{\prime }}_i+O(\; h\; 5\; )\end{array}$

另外， $f_i$ 和 ${f^{\prime }}_i$ $\left(i=0,1,2\right)$ 可以由 $I_0,I_1,I_2,I_3,I_4,I_5$ 得到，由对称性可以得到 $f_i$ 和 ${f^{\prime }}_i$ $\left(i=n-2,n-1,n\right)$ 的逼近值。

定理2对于端点处函数值以及一阶导数值有

${\tilde{f}}_0=\frac{1}{60h}\left(147I_0-213I_1+237I_2-163I_3+62I_4-10I_5\right)=f_0+O(\; h\; 5\; )$

${\tilde{f}}_1=\frac{1}{60h}\left(10I_0+87I_1-63I_2-37I_3-13I_4+2I_5\right)=f_1+O(\; h\; 5\; )$

${\tilde{f}}_2=\frac{1}{60h}\left(-2I_0+22I_1+57I_2-23I_3+7I_4-I_5\right)=f_2+O(\; h\; 5\; )$

${\tilde{f}}_{n-2}=\frac{1}{60h}\left(-2I_{n-1}+22I_{n-2}+57I_{n-3}-23I_{n-4}+7I_{n-5}-I_{n-6}\right)=f_{n-2}+O(\; h\; 5\; )$

${\tilde{f}}_{n-1}=\frac{1}{60h}\left(10I_{n-1}+87I_{n-2}-63I_{n-3}+37I_{n-4}-13I_{n-5}+2I_{n-6}\right)=f_{n-1}+O(\; h\; 5\; )$

${\tilde{f}}_n=\frac{1}{60h}\left(147I_{n-1}-213I_{n-2}+237I_{n-3}-163I_{n-4}+62I_{n-5}-10I_{n-6}\right)=f_n+O(\; h\; 5\; )$

${{\tilde{f}}^{\prime }}_0=\frac{1}{180h^2}\left(-812I_0+2320I_1-2945I_2+2135I_3-835I_4+137I_5\right)={f^{\prime }}_0+O(\; h\; 5\; )$

${{\tilde{f}}^{\prime }}_1=\frac{1}{180h^2}\left(-137I_0+10I_1+265I_2-205I_3+80I_4-13I_5\right)={f^{\prime }}_1+O(\; h\; 5\; )$

${{\tilde{f}}^{\prime }}_2=\frac{1}{180h^2}\left(13I_0-215I_1+205I_2+5I_3-10I_4+2I_5\right)={f^{\prime }}_2+O(\; h\; 5\; )$

${{\tilde{f}}^{\prime }}_{n-2}=\frac{1}{180h^2}\left(-13I_{n-1}+215I_{n-2}-205I_{n-3}-5I_{n-4}+10I_{n-5}-2I_{n-6}\right)={f^{\prime }}_{n-2}+O(\; h\; 5\; )$

${{\tilde{f}}^{\prime }}_{n-1}=\frac{1}{180h^2}\left(137I_{n-1}-10I_{n-2}-265I_{n-3}+205I_{n-4}-80I_{n-5}+13I_{n-6}\right)={f^{\prime }}_{n-1}+O(\; h\; 5\; )$

${{\tilde{f}}^{\prime }}_n=\frac{1}{180h^2}\left(812I_{n-1}-2320I_{n-2}+2945I_{n-3}-2135I_{n-4}+835I_{n-5}-137I_{n-6}\right)={f^{\prime }}_n+O(\; h\; 5\; )$

证明：将f在 $x_0$ 处展开

$f\left(x\right)={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{f_0^{\left(j\right)}}{j!}}{\left(x-x_0\right)}^j$

$\begin{array}{c}{I}_0={\displaystyle {\int }_{x_0}^{x_1}f\left(x\right)\text{d}x}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{f_i^{\left(j\right)}}{j!}{\displaystyle {\int }_{x_0}^{x_1}{\left(x-x_0\right)}^j\text{d}x}}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{h^{j+1}}{\left(j+1\right)!}{f}_0^{\left(j\right)}}\\ =f_{0}h+\frac{{f^{\prime }}_0}{2!}{h}^2+\frac{{f^{″}}_0}{3!}{h}^3+\frac{{f^{‴}}_0}{4!}{h}^4+\frac{f_0^{\left(4\right)}}{5!}{h}^5+\frac{f_0^{\left(5\right)}}{6!}{h}^6+O(\; h\; 7\; )\end{array}$

同理可得

$\begin{array}{c}{\displaystyle \underset{i=0}{\overset{1}{\sum }}{I}_i}={\displaystyle {\int }_{x_0}^{x_2}f\left(x\right)\text{d}x}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{f_i^{\left(j\right)}}{j!}{\displaystyle {\int }_{x_0}^{x_2}{\left(x-x_0\right)}^j}}\text{d}x={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{{\left(2h\right)}^{j+1}}{\left(j+1\right)!}{f}_0^{\left(j\right)}}\\ =f_0\left(2h\right)+\frac{{f^{\prime }}_0}{2!}{\left(2h\right)}^2+\frac{{f^{″}}_0}{3!}{\left(2h\right)}^3+\frac{{f^{‴}}_0}{4!}{\left(2h\right)}^4+\frac{f_0^{\left(4\right)}}{5!}{\left(2h\right)}^5+\frac{f_0^{\left(5\right)}}{6!}{\left(2h\right)}^6+O(\; h\; 7\; )\end{array}$

$\begin{array}{c}{\displaystyle \underset{i=0}{\overset{2}{\sum }}{I}_i}={\displaystyle {\int }_{x_0}^{x_3}f\left(x\right)\text{d}x}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{f_i^{\left(j\right)}}{j!}{\displaystyle {\int }_{x_0}^{x_3}{\left(x-x_0\right)}^j}}\text{d}x={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{{\left(3h\right)}^{j+1}}{\left(j+1\right)!}{f}_0^{\left(j\right)}}\\ =f_0\left(3h\right)+\frac{{f^{\prime }}_0}{2!}{\left(3h\right)}^2+\frac{{f^{″}}_0}{3!}{\left(3h\right)}^3+\frac{{f^{‴}}_0}{4!}{\left(3h\right)}^4+\frac{f_0^{\left(4\right)}}{5!}{\left(3h\right)}^5+\frac{f_0^{\left(5\right)}}{6!}{\left(3h\right)}^6+O(\; h\; 7\; )\end{array}$

$\begin{array}{c}{\displaystyle \underset{i=0}{\overset{3}{\sum }}{I}_i}={\displaystyle {\int }_{x_0}^{x_4}f\left(x\right)\text{d}x}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{f_i^{\left(j\right)}}{j!}{\displaystyle {\int }_{x_0}^{x_4}{\left(x-x_0\right)}^j}}\text{d}x={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{{\left(4h\right)}^{j+1}}{\left(j+1\right)!}{f}_0^{\left(j\right)}}\\ =f_0\left(4h\right)+\frac{{f^{\prime }}_0}{2!}{\left(4h\right)}^2+\frac{{f^{″}}_0}{3!}{\left(4h\right)}^3+\frac{{f^{‴}}_0}{4!}{\left(4h\right)}^4+\frac{f_0^{\left(4\right)}}{5!}{\left(4h\right)}^5+\frac{f_0^{\left(5\right)}}{6!}{\left(4h\right)}^6+O(\; h\; 7\; )\end{array}$

$\begin{array}{c}{\displaystyle \underset{i=0}{\overset{4}{\sum }}{I}_i}={\displaystyle {\int }_{x_0}^{x_5}f\left(x\right)\text{d}x}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{f_i^{\left(j\right)}}{j!}{\displaystyle {\int }_{x_0}^{x_5}{\left(x-x_0\right)}^j}}\text{d}x={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{{\left(5h\right)}^{j+1}}{\left(j+1\right)!}{f}_0^{\left(j\right)}}\\ =f_0\left(5h\right)+\frac{{f^{\prime }}_0}{2!}{\left(5h\right)}^2+\frac{{f^{″}}_0}{3!}{\left(5h\right)}^3+\frac{{f^{‴}}_0}{4!}{\left(5h\right)}^4+\frac{f_0^{\left(4\right)}}{5!}{\left(5h\right)}^5+\frac{f_0^{\left(5\right)}}{6!}{\left(5h\right)}^6+O(\; h\; 7\; )\end{array}$

$\begin{array}{c}{\displaystyle \underset{i=0}{\overset{5}{\sum }}{I}_i}={\displaystyle {\int }_{x_0}^{x_6}f\left(x\right)\text{d}x}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{f_i^{\left(j\right)}}{j!}{\displaystyle {\int }_{x_0}^{x_6}{\left(x-x_0\right)}^j}}\text{d}x={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\frac{{\left(6h\right)}^{j+1}}{\left(j+1\right)!}{f}_0^{\left(j\right)}}\\ =f_0\left(6h\right)+\frac{{f^{\prime }}_0}{2!}{\left(6h\right)}^2+\frac{{f^{″}}_0}{3!}{\left(6h\right)}^3+\frac{{f^{‴}}_0}{4!}{\left(6h\right)}^4+\frac{f_0^{\left(4\right)}}{5!}{\left(6h\right)}^5+\frac{f_0^{\left(5\right)}}{6!}{\left(6h\right)}^6+O(\; h\; 7\; )\end{array}$

由此，得到线性方程组

$\{\begin{array}{l}{f}_{0}h+\frac{{f^{\prime }}_0}{2!}{h}^2+\frac{{f^{″}}_0}{3!}{h}^3+\frac{{f^{‴}}_0}{4!}{h}^4+\frac{f_0^{\left(4\right)}}{5!}{h}^5+\frac{f_0^{\left(5\right)}}{6!}{h}^6+O\left(h^7\right)=I_0\\ f_0\left(2h\right)+\frac{{f^{\prime }}_0}{2!}{\left(2h\right)}^2+\frac{{f^{″}}_0}{3!}{\left(2h\right)}^3+\frac{{f^{‴}}_0}{4!}{\left(2h\right)}^4+\frac{f_0^{\left(4\right)}}{5!}{\left(2h\right)}^5+\frac{f_0^{\left(5\right)}}{6!}{\left(2h\right)}^6+O\left(h^7\right)={\displaystyle \underset{i=0}{\overset{1}{\sum }}{I}_i}\\ f_0\left(3h\right)+\frac{{f^{\prime }}_0}{2!}{\left(3h\right)}^2+\frac{{f^{″}}_0}{3!}{\left(3h\right)}^3+\frac{{f^{‴}}_0}{4!}{\left(3h\right)}^4+\frac{f_0^{\left(4\right)}}{5!}{\left(3h\right)}^5+\frac{f_0^{\left(5\right)}}{6!}{\left(3h\right)}^6+O\left(h^7\right)={\displaystyle \underset{i=0}{\overset{2}{\sum }}{I}_i}\\ f_0\left(4h\right)+\frac{{f^{\prime }}_0}{2!}{\left(4h\right)}^2+\frac{{f^{″}}_0}{3!}{\left(4h\right)}^3+\frac{{f^{‴}}_0}{4!}{\left(4h\right)}^4+\frac{f_0^{\left(4\right)}}{5!}{\left(4h\right)}^5+\frac{f_0^{\left(5\right)}}{6!}{\left(4h\right)}^6+O\left(h^7\right)={\displaystyle \underset{i=0}{\overset{3}{\sum }}{I}_i}\\ f_0\left(5h\right)+\frac{{f^{\prime }}_0}{2!}{\left(5h\right)}^2+\frac{{f^{″}}_0}{3!}{\left(5h\right)}^3+\frac{{f^{‴}}_0}{4!}{\left(5h\right)}^4+\frac{f_0^{\left(4\right)}}{5!}{\left(5h\right)}^5+\frac{f_0^{\left(5\right)}}{6!}{\left(5h\right)}^6+O\left(h^7\right)={\displaystyle \underset{i=0}{\overset{4}{\sum }}{I}_i}\\ f_0\left(6h\right)+\frac{{f^{\prime }}_0}{2!}{\left(6h\right)}^2+\frac{{f^{″}}_0}{3!}{\left(6h\right)}^3+\frac{{f^{‴}}_0}{4!}{\left(6h\right)}^4+\frac{f_0^{\left(4\right)}}{5!}{\left(6h\right)}^5+\frac{f_0^{\left(5\right)}}{6!}{\left(6h\right)}^6+O\left(h^7\right)={\displaystyle \underset{i=0}{\overset{5}{\sum }}{I}_i}\end{array}$

有

$\left(\begin{array}{cccccc}1& 1& 1& 1& 1& 1\\ 2& 2^2& 2^3& 2^4& 2^5& 2^6\\ 3& 3^2& 3^3& 3^4& 3^5& 3^6\\ 4& 4^2& 4^3& 4^4& 4^5& 4^6\\ 5& 5^2& 5^3& 5^4& 5^5& 5^6\\ 6& 6^2& 6^3& 6^4& 6^5& 6^6\end{array}\right)\left(\begin{array}{c}{f}_{0}h+O\left(h^7\right)\\ \frac{{f^{\prime }}_0}{2!}{h}^2+O\left(h^7\right)\\ \frac{{f^{″}}_0}{3!}{h}^3+O\left(h^7\right)\\ \frac{{f^{‴}}_0}{4!}{h}^4+O\left(h^7\right)\\ \frac{f_0^{\left(4\right)}}{5!}{h}^5+O\left(h^7\right)\\ \frac{f_0^{\left(5\right)}}{6!}{h}^6+O\left(h^7\right)\end{array}\right)=\left(\begin{array}{c}{I}_0\\ {\displaystyle \underset{i=0}{\overset{1}{\sum }}{I}_i}\\ {\displaystyle \underset{i=0}{\overset{2}{\sum }}{I}_i}\\ {\displaystyle \underset{i=0}{\overset{3}{\sum }}{I}_i}\\ {\displaystyle \underset{i=0}{\overset{4}{\sum }}{I}_i}\\ {\displaystyle \underset{i=0}{\overset{5}{\sum }}{I}_i}\end{array}\right)$

$\left(\begin{array}{c}{f}_{0}h+O\left(h^7\right)\\ \frac{{f^{\prime }}_0}{2!}{h}^2+O\left(h^7\right)\\ \frac{{f^{″}}_0}{3!}{h}^3+O\left(h^7\right)\\ \frac{{f^{‴}}_0}{4!}{h}^4+O\left(h^7\right)\\ \frac{f_0^{\left(4\right)}}{5!}{h}^5+O\left(h^7\right)\\ \frac{f_0^{\left(5\right)}}{6!}{h}^6+O\left(h^7\right)\end{array}\right)=\left(\begin{array}{cccccc}6& -\frac{15}{2}& \frac{20}{3}& -\frac{15}{4}& \frac{6}{5}& -\frac{1}{6}\\ -\frac{87}{10}& \frac{117}{8}& -\frac{127}{9}& \frac{33}{4}& -\frac{27}{10}& \frac{137}{360}\\ \frac{29}{6}& -\frac{461}{48}& \frac{31}{3}& -\frac{307}{48}& \frac{13}{6}& -\frac{5}{16}\\ -\frac{31}{24}& \frac{137}{48}& -\frac{121}{36}& \frac{107}{48}& -\frac{19}{24}& \frac{17}{144}\\ \frac{1}{6}& -\frac{19}{48}& \frac{1}{2}& -\frac{17}{48}& \frac{2}{15}& -\frac{1}{48}\\ -\frac{1}{120}& \frac{1}{48}& -\frac{1}{36}& \frac{1}{48}& -\frac{1}{120}& \frac{1}{720}\end{array}\right)\left(\begin{array}{c}{I}_0\\ {\displaystyle \underset{i=0}{\overset{1}{\sum }}{I}_i}\\ {\displaystyle \underset{i=0}{\overset{2}{\sum }}{I}_i}\\ {\displaystyle \underset{i=0}{\overset{3}{\sum }}{I}_i}\\ {\displaystyle \underset{i=0}{\overset{4}{\sum }}{I}_i}\\ {\displaystyle \underset{i=0}{\overset{5}{\sum }}{I}_i}\end{array}\right)$

得到

${\tilde{f}}_0=\frac{1}{60h}\left(147I_0-213I_1+237I_2-163I_3+62I_4-10I_5\right)=f_0+O(\; h\; 6\; )$

${{\tilde{f}}^{\prime }}_0=\frac{1}{180h^2}\left(-812I_0+2320I_1-2945I_2+2135I_3-835I_4+137I_5\right)={f^{\prime }}_0+O(\; h\; 5\; )$

用同样的方法，可以得到f在 $x_1,x_2,x_{n-2},x_{n-1},x_n$ 处的函数值及其一阶导数值。

3.2. 高精度积分值B样条拟插值格式

利用定理1和定理2中的 ${\tilde{f}}_i$ 和 ${{\tilde{f}}^{\prime }}_i$ 代替拟插值算子 ${\tilde{Q}}_{3,1}f\left(x\right)$ 中的 $f_i$ 和 ${f^{\prime }}_i$ ，得到高精度积分值B样条拟插值 $Q_{4}f(\; x\; )$

$Q_{4}f\left(x\right)={\displaystyle \underset{i=0}{\overset{n}{\sum }}\left[{\tilde{f}}_i+\frac{1}{4}{\tilde{f}}^{\prime }\left(x_i\right)\left(x-x_i\right)\right]H_i(\; x\; )}$

这样得到的高精度B样条拟插值算子是基于积分值的，不依赖于目标函数值和导数值。

3.3. 误差分析

下面对构造的拟插值算子 $Q_{4}f\left(x\right)$ 进行误差分析。

定理3对于任意函数 $f\in C^5\left[a,b\right]$ ，若 $x\in \left[a,b\right]$ ，则有

${\Vert Q_4^{\left(k\right)}f\left(x\right)-f^{\left(k\right)}\left(x\right)\Vert }_{\infty }=O\left(h^{5-k}\right),k=0,1,2,3$

证明

$\begin{array}{c}{\Vert Q_4^{\left(k\right)}f\left(x\right)-f^{\left(k\right)}\left(x\right)\Vert }_{\infty }={\Vert Q_4^{\left(k\right)}f\left(x\right)-{\tilde{Q}}_{3,1}^{\left(k\right)}f\left(x\right)+{\tilde{Q}}_{3,1}^{\left(k\right)}f\left(x\right)-f^{\left(k\right)}\left(x\right)\Vert }_{\infty }\\ \le {\Vert Q_4^{\left(k\right)}f\left(x\right)-{\tilde{Q}}_{3,1}^{\left(k\right)}f\left(x\right)\Vert }_{\infty }+{\Vert {\tilde{Q}}_{3,1}^{\left(k\right)}f\left(x\right)-f^{\left(k\right)}\left(x\right)\Vert }_{\infty }\end{array}$

由文献 [15] 中定理2.2，可以得到

${\Vert {\tilde{Q}}_{3,1}^{\left(k\right)}f\left(x\right)-f^{\left(k\right)}\left(x\right)\Vert }_{\infty }=O\left(h^{5-k}\right)$

且有

$\begin{array}{l}{\Vert Q_4^{\left(k\right)}f\left(x\right)-{\tilde{Q}}_{3,1}^{\left(k\right)}f\left(x\right)\Vert }_{\infty }\\ ={\Vert {\left[{\displaystyle \underset{i=0}{\overset{n}{\sum }}\left[{\tilde{f}}_i+\frac{1}{4}{f^{\prime }}_i\left(x-x_i\right)\right]H_i\left(x\right)}\right]}^{\left(k\right)}-{\left[{\displaystyle \underset{i=0}{\overset{n}{\sum }}\left[f_i+\frac{1}{4}{f^{\prime }}_i\left(x-x_i\right)\right]H_i\left(x\right)}\right]}^{\left(k\right)}\Vert }_{\infty }\\ ={\Vert \frac{k}{4}{\displaystyle \underset{i=0}{\overset{n}{\sum }}\left({{\tilde{f}}^{\prime }}_i-{f^{\prime }}_i\right)H_i^{\left(k-1\right)}\left(x\right)}+{\displaystyle \underset{i=0}{\overset{n}{\sum }}\left[\left({\tilde{f}}_i-f_i\right)+\frac{1}{4}\left({{\tilde{f}}^{\prime }}_i-{f^{\prime }}_i\right)\left(x-x_i\right)\right]H_i^{\left(k\right)}\left(x\right)}\Vert }_{\infty }\\ \le \frac{k}{4}\underset{0\le i\le n}{\max }\left|{{\tilde{f}}^{\prime }}_i-{f^{\prime }}_i\right|{\Vert {\displaystyle \underset{i=0}{\overset{n}{\sum }}{H}_i^{\left(k-1\right)}\left(x\right)}\Vert }_{\infty }+\underset{0\le i\le n}{\max }\left|\left({\tilde{f}}_i-f_i\right)+\frac{1}{4}\left({{\tilde{f}}^{\prime }}_i-{f^{\prime }}_i\right)\left(x-x_i\right)\right|{\Vert {\displaystyle \underset{i=0}{\overset{n}{\sum }}{H}_i^{\left(k\right)}\left(x\right)}\Vert }_{\infty }\end{array}$

对于 $\forall i$ ，有

${{\tilde{f}}^{\prime }}_i-{f^{\prime }}_i=O\left(h^5\right)$ ， ${\tilde{f}}_i-f_i=O(\; h\; 6\; )$

则有

${\Vert Q_4^{\left(k\right)}f\left(x\right)-{\tilde{Q}}_{3,1}^{\left(k\right)}f\left(x\right)\Vert }_{\infty }=O(\; h\; 5\; )$

所以

${\Vert Q_4^{\left(k\right)}f\left(x\right)-f^{\left(k\right)}\left(x\right)\Vert }_{\infty }=O\left(h^{5-k}\right)$

定理证明完毕。

4. 数值实例

本节用数值实例来验证本文方法是简单并且有效可行的。选取函数 $f\left(x\right)=\exp \left(x\right)$ ， $g\left(x\right)=\sin \left(\pi x\right)$ ，对于不同的值n，给出逼近函数及其相应的高阶导数的最大误差和数值收敛阶。

最大误差(maximum error ME)定义为

$M{E}^{\left(k\right)}\left(n\right)={\Vert Q_4^{\left(k\right)}f\left(x\right)-f^{\left(k\right)}\left(x\right)\Vert }_{\infty }$

对于 $f\left(x\right)$ ， $g\left(x\right)$ 及其高阶导数的最大误差见表1、表2。

Table 1. Maximum errors M E ( k ) ( n ) for f ( x )

表1. 对 $f\left(x\right)$ 的最大误差 $M{E}^{\left(k\right)}(\; n\; )$

Table 2. Maximum errors M E ( k ) ( n ) for g ( x )

表2. 对 $g\left(x\right)$ 的最大误差 $M{E}^{\left(k\right)}(\; n\; )$

由表1，表2可以看出，与Boujraf等人 [11] 提出的三次样条积分值拟插值算子逼近结果相比较，本文的拟插值算子对于原函数以及导函数有更好的逼近效果，并且文献 [11] 中的样条拟插值算子 ${\tilde{Q}}_{3}f\left(x\right)$ 只能逼近原函数、一阶导函数和二阶导函数，本文的拟插值算子还能较好的逼近三阶导函数。同时，对比文献 [16] 中的积分值四次样条拟插值 ${\tilde{Q}}_{4}f\left(x\right)$ ，虽然两者同为积分值四次样条拟插值，由数值实验结果可以看到本文的逼近效果是更优的，误差精度更小。对比吴金明等人 [13] 提出的积分值五次样条拟插值 ${\tilde{Q}}_{5}f\left(x\right)$ ，本文的拟插值算子与其整体逼近效果基本相当。

在表3，表4中相应列出了数值收敛阶(NCO)，其定义如下：

$NC{O}_k:=NC{O}_k\left(n\to 2n\right)=\frac{\ln \left(M{E}^{\left(k\right)}\left(n\right)/M{E}^{\left(k\right)}\left(2n\right)\right)}{\ln 2}$

对于 $f\left(x\right)$ ， $g\left(x\right)$ 的数值收敛阶见表3、表4。

Table 3. Numerical convergence orders NCOk for f ( x )

表3. 对 $f\left(x\right)$ 的数值收敛阶NCO_k

Table 4. Numerical convergence orders NCOk for g ( x )

表4. 对 $g\left(x\right)$ 的数值收敛阶NCO_k

由表3，表4可以看到，两个函数的数值收敛阶基本上与理论值吻合。

为了更直观的显示整体逼近效果，下面分别给出 $g\left(x\right)$ 和 $Q_{4}g\left(x\right)$ 、 $g^{\prime }\left(x\right)$ 和 ${Q^{\prime }}_{4}g\left(x\right)$ 、 $g^{″}\left(x\right)$ 和 ${Q^{″}}_{4}g\left(x\right)$ 、 $g^{‴}\left(x\right)$ 和 ${Q^{‴}}_{4}g\left(x\right)$ 的图像，见图1~图4 (取区间个数n = 10)。

从图1~图4可以看出，高精度积分值四次B样条拟插值在整体上可以很好的逼近原函数、一阶导函数、二阶导函数、三阶导函数。

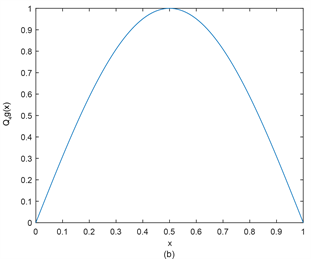
Figure 1. (a) Function $g\left(x\right)$ ; (b) Approximation function $Q_{4}g(\; x\; )$

图1. (a) 函数 $g\left(x\right)$ ；(b) 逼近函数 $Q_{4}g(\; x\; )$

Figure 2. (a) Function $g^{\prime }\left(x\right)$ ; (b) Approximation function ${Q^{\prime }}_{4}g(\; x\; )$

图2. (a) 函数 $g^{\prime }\left(x\right)$ ；(b) 逼近函数 ${Q^{\prime }}_{4}g(\; x\; )$

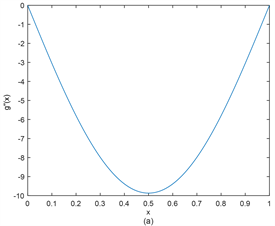
Figure 3. (a) Function $g^{″}\left(x\right)$ ; (b) Approximation function ${Q^{″}}_{4}g(\; x\; )$

图3. (a) 函数 $g^{″}\left(x\right)$ ；(b) 逼近函数 ${Q^{″}}_{4}g(\; x\; )$

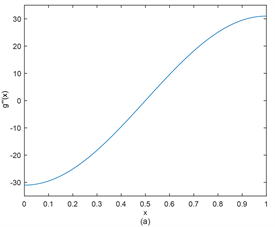
Figure 4. (a) Function $g^{‴}\left(x\right)$ ; (b) Approximation function ${Q^{‴}}_{4}g(\; x\; )$

图4. (a) 函数 $g^{‴}\left(x\right)$ ；(b) 逼近函数 ${Q^{‴}}_{4}g(\; x\; )$

5. 结语

本文给出的高精度积分值四次B样条拟插值算子来解决连续区间上积分值的函数重构问题，具有一定的优越性与创新性。本文的方法是利用连续区间的积分值的线性组合近似逼近结点处的函数值与一阶导数值，进而基于带导数信息的高精度B样条拟插值算子，得到高精度积分值四次B样条拟插值。该方法不需要解线性方程组，也不需要添加额外的目标函数信息，简单便于计算。同时通过数值实例的验证，本文的高精度积分值四次B样条拟插值与文献 [11] 中积分值三次样条拟插值算子相比，误差精度更高，同时能逼近更高阶的导函数；与文献 [16] 中四次样条拟插值相比较误差精度更高；与文献 [13] 中五次样条拟插值算子相比整体逼近效果相当。

NOTES

^*通讯作者。