如何比较两个无限集的元素“个数”？

How to Compare the “Number” of Elements of Two Infinite Sets?

摘要: 2019年人教版高中数学教科书必修第一册有一则“阅读与思考”材料–集合中元素的个数，其指出：有限集合中元素的个数可以一一数出来，便能通过比较自然数的大小直接比较有限集合元素个数的多少。而对于元素个数无限的集合，如N={0,1,2,…,n,…}，A={0,2,4,…,2n,…}无法一一数出集合中元素的个数，又该如何比较它们元素“个数”的多少呢？本文尝试类比比较两个有限集元素个数的方法，探讨如何比较两个无限集的元素“个数”。

Abstract: The first volume of the compulsory high school mathematics textbook of the 2019 People’s Education Edition has a “reading and thinking” material—the number of elements in the set, which points out that the number of elements in the finite set can be counted one by one, and the number of elements in the finite set can be directly compared by comparing the size of the natural number. For a set with an infinite number of elements, such as N={0,1,2,…,n,…} and A={0,2,4,…,2n,…}, the number of elements in the set can’t be counted one by one, so how to compare the number of their elements? This paper tries to compare the number of elements of two finite sets by analogy, and discusses how to compare the “number” of elements of two infinite sets.

1. 如何比较两个有限集的元素个数？

例如全班有45名学生，现有一箱苹果，每人分1个苹果，如何判断苹果是否够分呢？

一种判断的方法是数一数箱子里的苹果够不够45个。如果苹果个数不小于45，那么这箱苹果就够分。如果苹果个数小于45，则说明这箱苹果不够分。即可以通过“数一数”的方法来比较箱子里苹果个数和全班人数的多少。

实际上，我们可能不会把箱子里的苹果全部繁琐地数一遍。因此，一种操作性的判断方法是，直接给45名学生1人分1个苹果。如果每名学生都能分到苹果，且箱子里的苹果没有剩余，表明苹果恰好有45个，即苹果的个数和学生人数一样多。如果每名学生都分到了苹果，且箱子里的苹果有剩余，表明苹果多于45个，即苹果的个数大于学生人数。如果存在学生没有分到苹果，表明苹果少于45个，即苹果的个数小于学生人数。

上述两种方法——“数一数”和“1人分1个苹果”都能用来比较两个有限集元素个数的多少，那么它们也都能用来比较两个无限集元素“个数”多少吗？显然，无限集的元素“个数”无法一一数出来，因此只能通过“1人分1个苹果”的方法比较两个无限集元素“个数”的多少。

2. 集合等势的概念

“1人分1个苹果”本质上是数学中的一一映射，如果全班45名学生能够和这箱苹果建立一一映射，表明学生人数和苹果个数相等，即这两个集合的元素“个数”是一样多的。

将这个问题一般化，怎样判断两个集合元素“个数”是否相等呢？只需看它们是否能够建立一一映射。如果两个集合能够建立一一映射，称这两个集合等势，记作 $A\sim B$ [1] 。

显然，等势集合的元素“个数”(集合的“势”)相等，也称两个集合有相同的基数。

3. 如何比较两个无限集的元素“个数”？

由此看来，若想比较两个无限集的元素“个数”，只需看其是否能够建立一一映射。如果能够建立一一映射，说明两个集合元素“个数”一样多，如果不能建立一一映射，那么含有剩余元素的集合元素“个数”多。下面利用集合等势的概念，比较无限集合元素“个数”的多少。

例1 已知自然数集 $N=\left\{0,1,2,\cdots ,n,\cdots \right\}$ ，其中的偶数集 $A=\left\{0,2,4,\cdots ,2n,\cdots \right\}$ ，比较自然数的“个数”和其中偶数的“个数”的多少。

或许你会脱口而出，自然数集是一个整体，而偶数集是自然数集的一部分，“整体”当然大于“部分”，所以自然数的“个数”显然比其中的偶数的“个数”多。

上述直观的认识是不正确的，实际上自然数的“个数”与其中偶数的“个数”是一样多的。

根据等势的概念，如果两个集合能够建立一一映射，表明两个集合元素“个数”相等。显然可以建立自然数集和偶数集之间如图1所示的一一映射，从而自然数集与偶数集等势，即自然数的“个数”和其中的偶数的“个数”一样多。

Figure 1. One-to-one mapping between natural numbers and even numbers

图1. 自然数与偶数建立的一一映射

例2 如图2，2 cm的线段 $AB$ 和4 cm的线段 $CD$ 比较(如图2)，哪条线段上的点多？

Figure 2. Line segment AB and CD

图2. 线段AB和CD

可能你会直观地基于4 cm的线段比2 cm的线段长，得出4 cm的线段比2 cm的线段上的点多，实际上这两条线段上的点是一样多的。

同样，我们尝试建立2 cm线段上的点到4 cm线段上的点的一一映射。

如图3，将 $AB$ 和 $CD$ 置于互相平行的位置，连结 $CA$ ， $DB$ 交于点 $O$ 。在 $AB$ 上任取一点，连结 $OP$ 交 $CD$ 于点 $P^{\prime }$ 。这样的情形类似以 $O$ 为点光源，将线段 $AB$ 上点 $P$ 投影到线段 $CD$ 上。显然，对于线段 $AB$ 上任意两个不同的点 $P_1$ 和 $P_2$ ，在线段 $CD$ 上总有不同的点 ${P^{\prime }}_1$ 和 ${P^{\prime }}_2$ 与之对应，同时线段 $CD$ 上的任意一点 $P^{\prime }$ 在线段 $AB$ 上都能找到原象 $P$ 。

Figure 3. A one-to-one mapping of line segment AB and CD

图3. 线段AB和CD的一种一一映射

这样，我们就建立了线段 $AB$ 上的点到线段 $CD$ 上的点之间一一映射，从而线段 $AB$ 上的点集与线段 $CD$ 上的点集等势，即线段 $AB$ 上的点和线段 $CD$ 上的点一样多 [2] 。

例3 实数集 $R$ 和开区间(0, 1)内的实数哪个多？

或许你会直观地基于开区间(0, 1)是实数集 $R$ 的真子集，认为全体实数比开区间(0, 1)内的实数多，实际上开区间(0, 1)和全体实数一样多。

同样，我们尝试建立开区间(0, 1)到实数集 $R$ 的一一映射。

函数 $y={\log }_2\sqrt{\frac{1-x}{x}}$ 的定义域是(0, 1)，值域是实数集 $R$ ，函数关系是一一映射，即开区间(0, 1)内任意两个不同的实数 $x_1$ 和 $x_2$ ，在实数集 $R$ 上总能找到两个不同的实数 $y_1$ 和 $y_2$ 与之对应，同时实数集 $$ 上的任意一个实数 $y$ 在开区间(0, 1)内都能找到某个 $x$ 与之对应。

这就建立了开区间(0, 1)到实数集 $R$ 的一一映射(图4)。从而开区间(0, 1)与实数集 $R$ 等势，即开区间(0, 1)上的实数和全体实数一样多。

上述三个例子都建立了两个无限集之间的一一映射，说明三对集合都是等势的，即它们的元素“个数”是相等的。

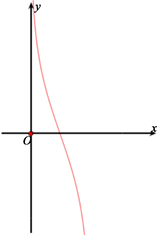
Figure 4. A one-to-one mapping from the open interval (0, 1) to the set of real numbers

图4. 开区间(0, 1)到实数集的一个一一映射

同时可以发现，例1中，自然数集是“整体”，其中的偶数集是自然数集的“部分”；例2中，4 cm的线段是“整体”，2 cm的线段是它的“部分”；例3中，实数集 $R$ 是“整体”，开区间(0, 1)是实数集 $R$ 的“部分”。这三个例子均得出“整体”等于“部分”的结论，这颠覆了“整体”大于“部分”的直观认识。

这个结论在历史上也困扰着众多数学家和逻辑学家。而康托尔认为这恰恰是无限集的本质特征，也就是只有无限集才可能出现“整体=部分”的现象。换言之，只有通过集合等势的关系才可以定义无限集，即如果集合 $A$ 可以和其真子集建立等势关系，则这个集合一定是无限集。据此可知，苏教版高中数学必修第一册中把“含有无限个元素的集合称为无限集”，实际是用“无限”定义“无限集”的逻辑循环错误。

4. “无穷”也有大小之分

上述三个例子中集合的元素“个数”分别对应相等，并且其元素个数均为“无穷”，是否意味着所有无限集的元素“个数”都是一样大的“无穷”呢？换言之，“无穷”是否也有大小呢？

事实上，数学家严格证明了无限集的元素“个数”(即“无穷”)也是有大小的。数学家将能与自然数集 $N$ 建立一一映射的无限集的“无穷”定义为最小的“无穷”，称为阿列夫零，记作 ${\aleph }_0$ ，并将这样的集合叫做“可数集”。例如偶数集、奇数集都是可数集。同时数学家严格证明了有理数集也是可数集，即有理数集和自然数集等势，有理数和自然数的“个数”一样多。

进而数学家康托尔严格证明了比自然数集这类可数集的“无穷”大的下一个“无穷”，是指能与实数集建立等势关系的集合的“无穷”，叫做阿列夫一，记作 ${\aleph }_1$ 。例如(0, 1)、[2, 5]、(4, 8]等区间元素“个数”的“无穷”都是阿列夫一。阿列夫一是比阿列夫零大的“无穷”，即实数集的“无穷”比自然数集的“无穷”大。康托尔利用“对角线法”严格证明了此结论，其证明方法如下：

证明：实数集不能与自然数集建立一一映射，即实数集 $R$ 是不可数集。

分析：由例3知 $R\sim \left(0,1\right)$ ，要证明实数集 $R$ 是不可数集，只需证明开区间(0, 1)是不可数集。根据集合等势的概念，只需证明开区间(0, 1)不能与自然数集建立一一映射即可。

现利用反证法：假设开区间(0, 1)与自然数集等势。把开区间(0, 1)内每个实数 $a_n$ 唯一地表示为十进位无穷小数 $a_n=0.a_{n1}{a}_{n2}{a}_{n3}\cdots a_{nn}\cdots$ 的形式，其中 $a_{ni}$ 是 $0,1,\cdots ,9$ 中的一个数字，不全为9，且不以0为循环节。

这样开区间 $\left(0,1\right)=\left\{a_1,a_2,a_3,\cdots ,a_n,\cdots \right\}$ ，其中

$\begin{array}{l}{a}_1=0.a_{11}{a}_{12}{a}_{13}\cdots a_{1n}\cdots \\ a_2=0.a_{21}{a}_{22}{a}_{23}\cdots a_{2n}\cdots \\ a_3=0.a_{31}{a}_{32}{a}_{33}\cdots a_{3n}\cdots \\ \cdots \\ a_n=0.a_{n1}{a}_{n2}{a}_{n3}\cdots a_{nn}\cdots \\ \cdots \end{array}$

利用对角线上数字 $a_{nn}\left(n=1,2,\cdots \right)$ 构造开区间(0, 1)内的一个实数如下：

$x=0.x_1{x}_2{x}_3\cdots x_n\cdots$

其中 $x_1\ne a_{11},x_2\ne a_{22},x_3\ne a_{33},\cdots ,x_n\ne a_{nn},\cdots$ ，从而实数 $x\ne a_1,x\ne a_2,x\ne a_3,\cdots ,x\ne a_n,\cdots$ ，故而 $x$ 不属于 $\left(0,1\right)=\left\{a_1,a_2,a_3,\cdots ,a_n,\cdots \right\}$ ，这样出现了矛盾： $x=0.x_1{x}_2{x}_3\cdots x_n\cdots$ 是开区间(0, 1)内的一个实数，但这个数又不属于开区间(0, 1)。之所以出现矛盾，原因就在于假设开区间(0, 1)与自然数集等势，从而假设不成立，因此开区间(0, 1)是不可数集，所以实数集的“无穷”比自然数集的“无穷”大。

我们知道，若有限集 $A$ 的元素个数为 $n$ ，这个有限集的所有子集构成的集合 $M$ (有限集 $A$ 的幂集)的元素个数是 $2^n$ ，显然 $2^n>n$ 。这样的关系可以类比到无限集。设集合 $B$ 是一个无限集，它的元素“个数”为 $\aleph$ ，其幂集 $P$ 的元素“个数”是 $2^{\aleph }$ ，且 $2^{\aleph }>\aleph$ 。

可见，任何一个无限集幂集的元素“个数”比这个无限集的元素“个数”多(cantor定理) [3] ，即“无穷”也有大小之分。自然数集 $N$ 这个无限集的“无穷”为最小的“无穷” ${\aleph }_0$ ，自然数集 $N$ 的幂集与实数集等势，其元素“个数”为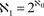，实数集幂集的元素“个数”为 ${\aleph }_2=2^{{\aleph }_1}$ ，以此类推，得到“无穷”的大小关系如下：

5. 结束语

本文从比较两个有限集元素个数“1人分1个苹果”的方法入手，从中抽象出集合等势的概念，进而利用等势概念解决了如何比较无限集的“元素个数”的问题，并得到刻画不同无限集“元素个数”的“无穷”也有大小的深刻认识。这样的思考过程和结果深刻彰显数学学科独有的抽象性、逻辑性和严密性。