监控广义线性Profile数据的变样本容量动态控制图

Dynamic Control Charts with Variable Sample Size for Monitoring Generalized Linear Profile Data

摘要: 对于离散响应变量的profile数据，比如二元的、多项的、次序的和Poisson响应的profile，进行有效的监控越来越受到统计过程控制领域研究人员的关注。这些profile都可看作广义线性模型的特殊情况。本文提出了一种基于加权似然比检验的第二阶段的变样本容量动态控制图用来监控广义线性profile数据。不仅能增强对中小漂移的检测敏感度，还可以提高检测的速度, 降低抽样成本，提高企业统计决策的精确度和可靠度。通过平均运行长度来衡量控制图的性能表现，模拟结果表明，与静态控制图相比，所提出的控制图对于模型参数的变化有很好的监控能力。

Abstract: In recent years, effective profile monitoring for discrete response variables, such as binary, multinomial, ordinal or Poisson variables, has increasingly attracted interest of researchers in the area of statistical process control. Such quality characteristics are often modeled as special cases of generalized linear models. A new control chart is developed based on the weighted likelihood ratio test with adaptive sample sizes, which is used to monitoring generalized linear profile data. It can not only enhance the sensitivity of detecting small and medium-sized shift, but it can also improve the speed of detection, reduce sampling costs, and improve the accuracy and reliability of enterprise statistical decision-making. The performance of the control chart is measured by the average running length, and the simulation results show that compared with the static control chart, the proposed control chart has good monitoring ability for changes in model parameters.

1. 引言

随着现代工业技术的发展，精密制造业的生产过程日趋复杂，有关产品质量的问题已不能被某个或某几个指标的均值或方差(或分布)来完全代表或解释，而是需要用profile数据对过程进行更加精细和完整地刻画。Profile数据指的是在抽样点上，我们所得到的观测值可以看作是一些回归曲线。

统计过程控制中对profile数据(连续响应变量或离散响应变量)的监控方法已非常丰富，参见文献 [1] [2] 或专著 [3] 。关于离散响应变量的profile，Yeh et al. [4] 开创性地研究了用于监控二元响应变量的profile的第二阶段(Phase II)的控制图。之后，学者们分别提出了用于监控响应变量是Poisson的、次序的和多项的profile的第二阶段的控制图 [5] [6] [7] 。这里，响应变量是二元的、Poisson的、次序的和多项的profile都可以看作是广义线性模型的特例。在广义线性模型的统一框架下，Amiri et al. [8] 和Shadman et al. [9] 建立了第一阶段(Phase I)的控制图，Qi et al. [10] 建立了第二阶段的控制图。

以上的文献都是以固定的抽样间隔抽取固定数量的样本，而一个非常直观的想法是当一个控制图的检验统计量距离控制线较近，过程失控的可能性比较大时，我们就会以一个较短的抽样间隔抽取较多数量的样本，来达到对当前过程信息更好地了解的目的；反之，当一个控制图的检验统计量距离控制线较远，过程失控的可能性比较小时，我们就可以以一个较长的抽样间隔抽取较少数量的样本，这就是动态控制图的思想 [11] 。尚云艳 [12] 建立了基于似然比的变样本容量动态控制图监控正态数据。Kazemzadeh et al. [13] 建立了变样本容量的动态控制图监控简单线性profile数据。Mohammadzadeh et al. [14] 建立了变抽样区间的动态控制图监控二元响应变量的profile数据。

综上，关于离散响应变量的profile，本文考虑在广义线性模型的统一框架下，给出变样本容量的第二阶段控制图监控模型的系数是否发生漂移。通过加权似然比检验建立监控统计量，设置报警限和警戒限，当监控统计量小于警戒限时抽取较少的样本，当监控统计量大于警戒限时抽取较多的样本，当监控统计量大于报警限时，发出过程失控的警报。通过蒙特卡洛模拟，所提出的控制图具有较好的表现。

2. 变点模型

假设在生产过程中收集到的profile数据之间是独立的，在第i时刻抽取 $n_i$ 个样本，随机样本简记为 $\left(X_{ij},y_{ij}\right)$ ， $i=1,2,\cdots ,t$ ， $j=1,\cdots ,n_i$ ，其中 $X_{ij}$ 是解释变量， $y_{ij}$ 是响应变量， $n_i$ 为随时间变化的样本量。进一步假设数据满足以下广义线性模型：

1) 响应变量 $Y_i={\left(y_{i1},\cdots ,y_{i{n}_i}\right)}^{{\rm T}}$ 是独立同分布，服从于指数分布族的随机变量，其中 $y_{ij}$ 是在时刻i的第j个样本的响应变量，响应变量 $y_{ij}$ 的概率密度函数为

$f\left(y_{ij};{\theta }_{ij}\right)=\exp \left[y_{ij}b\left({\theta }_{ij}\right)+c\left({\theta }_{ij}\right)+d\left(y_{ij}\right)\right],i=1,2,\cdots ,t;j=1,\cdots ,n_i$

其中 $b\left({\theta }_{ij}\right),c\left({\theta }_{ij}\right),d\left(y_{ij}\right)$ 是已知函数， $l_i^{\text{'}}(\beta )={\displaystyle \underset{j=1}{\overset{n_i}{\sum }}\left[y_{ij}b({\theta }_{ij})+c({\theta }_{ij})+d(y_{ij})\right]}，i=1,\mathrm{...},t$ 是自然参数。

2) 解释变量

$X_i=\left(\begin{array}{c}{X}_{i1}^{\text{T}}\\ ⋮\\ X_{i{n}_i}^{\text{T}}\end{array}\right)=\left(\begin{array}{ccc}{x}_{i1,1}& \cdots & x_{i1,p}\\ ⋮& & ⋮\\ x_{i{n}_i,1}& \cdots & x_{i{n}_i,p}\end{array}\right)$

为一个设定的 $n_i\times p$ (且 $p<n_i$ )维矩阵，其中 $X_{ij}^{\text{T}}=\left(x_{ij,1},\cdots ,x_{ij,p}\right)$ ， $i=1,2,\cdots ,t$ ， $j=1,\cdots ,n_i$ 。

3) 解释变量 $X_{ij}^{\text{T}}$ 与回归系数 $\beta$ 的一个单调链接函数如下：

$g\left({\mu }_{ij}\right)={\eta }_{ij}=X_{ij}^{\text{T}}\beta$

其中 ${\mu }_{ij}=E\left(Y_{ij}\right)$ ，且回归系数向量 $\beta ={\left({\beta }_1,\cdots ,{\beta }_p\right)}^{\text{T}}$ ， $p<n_i$ ， $i=1,2,\cdots ,t$ ， $j=1,2,\cdots ,n_i$ 。

假设在一个未知的 $\tau$ 时刻，生产过程失控，即系数 $\beta$ 由可控时的 ${\beta }_{IC}$ 变为失控时的 ${\beta }_{OC}$ 。于是，在每一时刻 $t=1,2,\cdots$ 监控以下变点模型：

$\{\begin{array}{l}{H}_0:\beta ={\beta }_{IC}\\ H_1:\beta ={\beta }_{OC}\end{array}$

3. 在线监控方法

首先求加权似然比监控统计量，在第t时刻的对数似然函数为

${l^{\prime }}_i\left(\beta \right)={\displaystyle \underset{j=1}{\overset{n_i}{\sum }}\left[y_{ij}b\left({\theta }_{ij}\right)+c\left({\theta }_{ij}\right)+d\left(y_{ij}\right)\right],i=1,2,\cdots ,t}$

从而加权对数似然函数为

$w{l^{\prime }}_t\left(\beta \right)={\displaystyle \underset{i=0}{\overset{t}{\sum }}{w}_i{l^{\prime }}_i\left(\beta \right)}={\displaystyle \underset{i=0}{\overset{t}{\sum }}{w}_i{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}\left[y_{ij}b\left({\theta }_{ij}\right)+c\left({\theta }_{ij}\right)+d\left(y_{ij}\right)\right]}}$

其中 $w_0={\left(1-\lambda \right)}^t$ ， $w_i=\lambda {\left(1-\lambda \right)}^{t-i}$ ， $i=1,2,\cdots ,t$ ， $\lambda \in \left(0,1\right)$ 是光滑参数。

令 ${\Im }^{\left(m-1\right)}={\displaystyle \underset{i=1}{\overset{t}{\sum }}{w}_i{\Im }_i^{\left(m-1\right)}}$ 为信息矩阵， $U^{\left(m-1\right)}={\displaystyle \underset{i=0}{\overset{t}{\sum }}{w}_i{U}_i^{\left(m-1\right)}}$ 为得分矩阵，由牛顿迭代法 [10] ，根据公式

${\beta }^{\left(m\right)}={\beta }^{\left(m-1\right)}+{\left[{\Im }^{\left(m-1\right)}\right]}^{-1}{U}^{\left(m-1\right)}$

可得系数 $\beta$ 的加权极大似然估计 ${\stackrel{⌢}{\beta }}_t=\arg {\max }_{\beta }w{l^{\prime }}_t\left(\beta \right)$ 。

于是，构造如下变样本容量的加权似然比检验统计量(VSS-WLRT)

${W^{\prime }}_t=2{\displaystyle \underset{i=0}{\overset{t}{\sum }}{w}_i\left\{{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}\left[y_{ij}b\left({\hat{\theta }}_{ij}\right)+c\left({\hat{\theta }}_{ij}\right)+d\left(y_{ij}\right)/\sqrt{n_i}\right]}-{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}\left[y_{ij}b\left({\theta }_{ij}\right)+c\left({\theta }_{ij}\right)+d\left(y_{ij}\right)/\sqrt{n_i}\right]}\right\}}$

然后，根据公式 $n_1{p}_1+n_2{p}_2=n_0$ 设置报警限h和警戒限g，其中 $p_1={\rm P}\left[{W^{\prime }}_t\in \left(g,h\right)\right]$ ， $p_2={\rm P}\left[{W^{\prime }}_t\in \left(0,g\right)\right]$ ， $n_0$ 为固定样本容量的控制图的抽取样本量， $n_1<n_0<n_2$ 且 $p_1+p_2=1$ 。

在时刻t，当统计量 $g<{W^{\prime }}_t<h$ 时，在下一时刻抽取较大的容量为 $n_2$ 的样本；当统计量 ${W^{\prime }}_t<g$ 时，在下一时刻抽取较小的容量为 $n_1$ 的样本；当统计量 ${W^{\prime }}_t>h$ 时，此时控制图发出系数 $\beta$ 发生漂移的警报。

变样本容量动态控制图监控过程的流程图如图1所示。

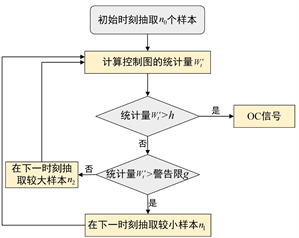
Figure 1. Flow chart of dynamic control chart monitoring with variable sample size

图1. 变样本容量动态控制图监控的流程图

4. 统计模拟与示例

通过蒙特卡洛模拟将本文所提出的方法(简记为VSS-WLRT)与Qi et al. [10] 的WLRT方法进行比较。参考Qi et al. [10] 响应变量是Poisson分布的统计模拟，当过程参数可控时给定 ${\beta }_i={\beta }_{IC}={\left(1,1\right)}^{{\rm T}}$ ，过程参数失控时 ${\beta }_i={\beta }_{IC}+\Delta$ ，其中 $\Delta ={\left({\delta }_1{\sigma }_1,{\delta }_2{\sigma }_2\right)}^{{\rm T}}$ ， ${\delta }_1,{\delta }_2$ 为漂移量且不同时为0， ${\sigma }_1=0.35181$ ， ${\sigma }_2=0.50947$ 。参考文献 [13] ，在进行动态控制图与静态控制图比较时，应设定具有相同的平均采样率，本文设定 $p_1=p_2=0.5$ ，此时样本容量设置为 $\left(n_0,n_1,n_2\right)=\left(5,2,8\right)$ 时，控制图记为VSS-WLRT₁；样本容量设置为 $\left(n_0,n_1,n_2\right)=\left(5,3,7\right)$ 时，控制图记为VSS-WLRT₂。通过二分法调整控制限使得不同控制图可控时的平均运行长度ARL₀接近370，然后比较失控时的平均运行长度ARL₁。失控状态下的ARL₁越小，控制图报警越早，监控效果越好。在理论上，WLRT和VSS-WLRT控制图的监控效果都受到光滑参数的影响，较大的光滑参数对大漂移较有效，较小的光滑参数对小漂移较有效。因此，在光滑参数 $\lambda$ 分别取0.05，0.1和0.2的情况下，进行5000次重复模拟得到各控制图的ARL₁，见表1、表2和表3。

Table 1. ARL1 the control chart of the WLRT, VSS-WLRT1, VSS-WLRT2 when λ = 0.05

表1. $\lambda =0.05$ 时WLRT、VSS-WLRT₁、VSS-WLRT₂的失控ARL₁

由表1~表3可以看出，相同漂移的情况下，VSS-WLRT₁与VSS-WLRT₂两个动态控制图的ARL₁均比静态WLRT控制图的更小，从而监控效果更好。例如，在 $\lambda =0.05$ ，漂移量 $\left({\delta }_1,{\delta }_2\right)=\left(0.2,0\right)$ 时，WLRT控制图的ARL₁为143.5650，VSS-WLRT₁的ARL₁为87.8400，VSS-WLRT₂的ARL₁为74.7350；漂移量 $\left({\delta }_1,{\delta }_2\right)=\left(0.59,0.59\right)$ 时，WLRT控制图的ARL₁为7.5540，而VSS-WLRT₁的ARL₁为3.2420，VSS-WLRT₂的ARL₁为3.8320。因此表明，在不同的漂移量下，变样本容量的动态控制图的报警速度均比静态控制图更快。

Table 2. ARL1 the control chart of the WLRT, VSS-WLRT1, VSS-WLRT2 when λ = 0.1

表2. $\lambda =0.1$ 时WLRT、VSS-WLRT₁、VSS-WLRT₂的失控ARL₁

由表1~表3还可以看出，三个控制图的监控效果受到光滑参数的影响。 $\lambda =0.2$ ，对大漂移比较有效； $\lambda =0.05$ ，对小漂移比较有效。例如，当漂移量 $\left({\delta }_1,{\delta }_2\right)=\left(0.59,0.59\right)$ 时， $\lambda =0.2$ 的VSS-WLRT₁控制图的ARL₁ = 1.4172， $\lambda =0.05$ 的VSS-WLRT₁控制图的ARL₁ = 3.2420；当漂移量 $\left({\delta }_1,{\delta }_2\right)=\left(0.2,0\right)$ 时， $\lambda =0.05$ 的VSS-WLRT₁控制图的ARL₁ = 87.8400， $\lambda =0.2$ 的VSS-WLRT₁控制图的ARL₁ = 185.3000，这一结果与理论一致。整体上看，与WLRT相比，VSS-WLRT控制图对中小漂移的检测敏感度有所提高。

Table 3. ARL1 the control chart of the WLRT, VSS-WLRT1, VSS-WLRT2 when λ = 0.2

表3. $\lambda =0.2$ 时WLRT、VSS-WLRT₁、VSS-WLRT₂的失控ARL₁

为了更好地理解所提出方法的应用，本文在 $\lambda =0.05$ ，漂移量 $\left({\delta }_1,{\delta }_2\right)=\left(0.5,0\right)$ 时，进行一次过程监控，给出如图2的示例(WLRT控制图中n取10)。由图2可以看出，固定样本量的WLRT控制图在t = 37时发出失控警报，VSS-WLRT₁控制图在t = 23时发出失控警报，VSS-WLRT₂在t = 16时发出失控警报。于是动态控制图所需的平均样本量更少，能达到降低成本的目的。

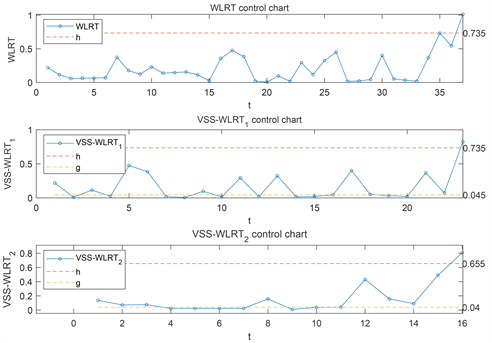
Figure 2. WLRT, VSS-WLRT₁, VSS-WLRT₂ control chart

图2. WLRT、VSS-WLRT₁、VSS-WLRT₂控制图

为了验证所提出方法对其它模型的适用性，本文扩展了Goeman和Cessie [15] 所讨论的多项式逻辑回归模型作为一个控制图性能比较的示例。在这里，我们只考虑解释变量是分类变量的情况，考虑一个有四个类别的响应变量Y。令 ${\pi }_1,\cdots ,{\pi }_4$ 表示响应变量各自类别的概率，且 ${\pi }_1+\cdots +{\pi }_4=1$ 。假设有三个取值为−1，0，1的协变量 $x_1$ 、 $x_2$ 、 $x_3$ 满足：

$\{\begin{array}{l}\log \left(\frac{{\pi }_2}{{\pi }_1}\right)=2x_1+\delta x_1^2,\\ \log \left(\frac{{\pi }_3}{{\pi }_1}\right)=2x_2,\\ \log \left(\frac{{\pi }_4}{{\pi }_1}\right)=2x_3.\end{array}$

取 $\lambda =0.1$ ， ${\text{ARL}}_0=\text{37}0$ ， $\tau =20$ ，可控时 $\delta =1$ ，失控时 $\delta =1.6$ 。在每个时间点t，从3个协变量值的3³=27种可能组合中随机抽取，获得25个观察数据集。VSS-WLRT₁控制图样本容量设置为 $\left(n_0,n_1,n_2\right)=\left(25,20,30\right)$ ，VSS-WLRT₂控制图样本容量设置为 $\left(n_0,n_1,n_2\right)=\left(25,15,35\right)$ ，WLRT控制图样本容量n设置为25。进行一次过程监控，绘制控制图如图3所示。

由图3可以看出，固定样本量的WLRT控制图在t = 47时发出失控警报，VSS-WLRT₁控制图在t = 28时发出失控警报，VSS-WLRT₂在t = 25时发出失控警报。变化样本量的动态控制图监测过程失控速度更快，且所需样本量更少，说明所提出方法对监控多项式逻辑回归模型也是适用的。

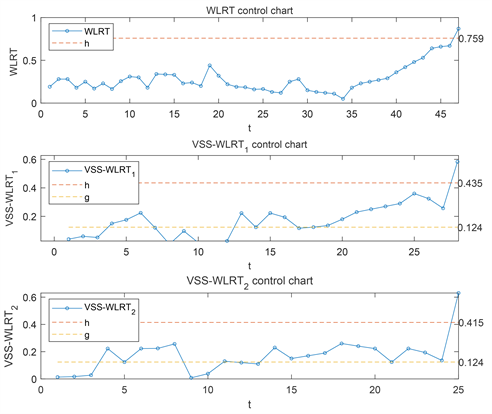
Figure 3. WLRT, VSS-WLRT₁, VSS-WLRT₂ control chart

图3. WLRT、VSS-WLRT₁、VSS-WLRT₂控制图

5. 结论

采用可变样本容量的方法建立动态的控制图，可以更有效地监测到生产过程失控，降低统计过程控制中的抽样成本。本文针对响应变量是离散型的profile数据，给出了在广义线性模型的统一框架下基于加权似然比检验的动态控制图。通过二分法统计模拟确定报警限和警戒限，当监控统计量小于警戒限时抽取较少的样本，当监控统计量大于警戒限时抽取较多的样本，达到降低抽样成本的目的。通过蒙特卡洛模拟得出，所提出的控制图失控时平均运行长度较小，具有较好的表现。广义线性模型是线性模型的推广，所以本文所提出的方法很容易应用于线性模型。本文的动态控制图是基于变样本容量提出，在之后的研究中还可以考虑变抽样区间对结果的影响。

基金项目

吉林省教育厅项目(JJKH20210809KJ)、国家自然科学基金面上项目(12271271)。