1. 引言
1970年至2021年期间 [1] ,共报告了近12,000起极端天气、气候和水灾害,造成200多万人死亡和4.3万亿美元的经济损失。预计2024年房地产企业面临的全球气候风险还将继续增加,针对风险建立提前预警机制,以便能采取主动规划或缓解措施是十分有益的。本文将通过模糊综合评价等方法为房地产公司提供决策依据 [2] 。
1.1. 麦肯锡逻辑树分析
麦肯锡分析问题最常使用的工具就是“逻辑树”。把一个已知问题当成树干,然后开始思考(头脑风暴)这个问题和哪些相关问题或者小问题有关。每想到一个问题,就给这个问题(也就是树干)加一个“树枝”,并标明这个“树枝”所代表的问题。一个大的“树枝”上还可以有小的“树枝”,如此类推,找出问题的所有相关联项目。由逻辑树分析确定的评价房地产投资可行性的指标有灾害程度,地区稳定性,建筑物等级,社区服务满意度和未来气候风险,逻辑树见图1:
1.2. 数据来源
灾害程度:灾害程度是指灾害的严重程度和对人类社会造成的影响。它可以通过人员伤亡情况、财产损失、社会和经济影响等方面的指标来衡量。本文收集三个城市历史极端天气次数和历史灾难死亡率数据进行TOPSIS结合熵权法的打分作为评价依据。
地区稳定性:地区稳定性是指一个特定区域在地质、环境和社会经济等多方面的相对稳定程度。这种稳定性可以受到多种因素的影响,包括地壳运动、自然灾害、环境变化、人口增长、经济发展等。本文把对应国家的人口密度数据作为评价依据。
建筑物等级:建筑物等级是指根据建筑物的耐久性、耐火性、设计等级等因素所划分的等级。这些等级有助于评估建筑物的质量、安全性和使用寿命,并为建筑物的使用、维护和改造提供指导。本文依据调查得来的各国建筑物等级排名作为评价依据。
社区服务满意度:社区服务满意度是指居民对社区提供的各项服务质量和效果的总体评价和感受。这些服务包括但不限于公共设施、环境卫生、文化活动、安全保障等方面 [3] 。本文依据本国居民对于本国政府的信任度评分作为评价依据。接下来通过气候预测,得出高温月份数作为未来气候风险的评价依据。
2. 气候预测
气候预测就是根据过去气候的演变规律,如温度,降水量,日照等,推断未来某个时间段内气候发展的可能趋势。由于气候有各种时间尺度的变化,从预测几十年以内的短期气候变化到预测万年以上冰期和间冰期的气候变迁,都属于气候预测的范畴。
前期我们一共收集了中国北京,德国柏林,摩洛哥卡萨布兰卡的月平均气温数据。我们选择中国北京月平均气温作为例子进行具体建模过程的展示,其它两个地方只列举最后结果。
2.1. 创建时间序列图
时间序列图是一种用于展示数据随时间变化的图形。它通常用于分析时间序列数据,即在不同时间点收集的数据序列。时间序列图可以用于识别数据的长期趋势、季节性变化以及周期性变化。例如,如果一个时间序列图显示数据在每年的同一时期都有相似的上升或下降趋势,那么这可能表明存在季节性影响。同样,如果数据呈现出固定的周期性变化,那么这可能表明存在某种周期性因素,如季节变化、经济周期等。本文通过SPSS软件创建的时间序列图见图2。
由图2我们可以看出中国北京的月平均气温波动稳定,且数据具有很强的季节性,因此可以使用加法分解模型。
2.2. 季节性分解
季节性分解 [4] 是根据时间序列数值的变化,将结果分为:长期变动趋势、季节变动规律、周期变动规律和不规则变动,由于变动组合的不确定性,数值变化随机出现在一个时间序列中。利用SPSS做出的季节因子统计表见表1。
由上表可知第1、2、3、11、12月份的季节因子为负,第4、5、6、7、8、9、10月份的季节因子为正,这说明中国北京的月平均气温在4、5、6、7、8、9、10月份要高于1、2、3、11、12月份,且7月份的月平均气温要高于全年平均气温14.035798℃。
做出分解后的时间序列图见图3。
由图3可知,季节调整因子(seasonally adjusted factor)成周期循环趋势,不规则变动(irregular variation)

Table 1. Seasonal factor statistics
表1. 季节因子统计表
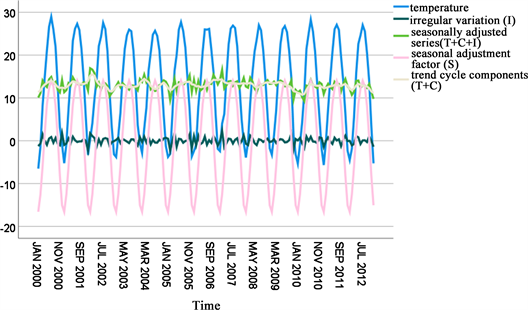
Figure 3. Decomposed time series plot
图3. 分解后的时间序列图
较为平稳并且趋于0,季节性调整后系列(seasonally adjusted series)和趋势循环成分(trend cycle components)近似为一条直线,选择趋势和循环成分数据用MATLAB工具箱进行拟合,拟合结果见图4:
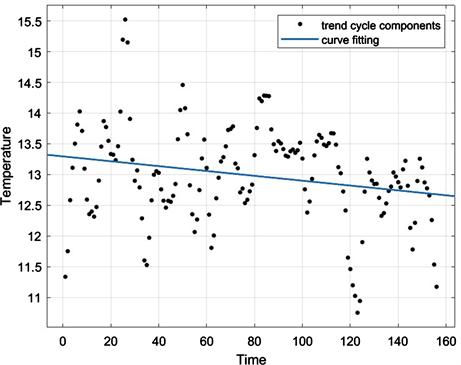
Figure 4. Trend cyclic component fitting plot
图4. 趋势循环成分拟合曲线图
计算求得拟合优度R2 = 0.0511,误差平方和SSE = 92.0756,拟合优度接近于1越好。由于该拟合优度和1相差巨大,误差平方和也较大,即使剔除异常值也无法达到理想的拟合效果,说明MATLAB工具箱不适合于对该数据预测。故本文接下来将选择SPSS的专家建模器进行预测。
2.3. 专家建模器
专家建模器 [5] 会自动査找每个相依序列的最佳拟合模型。如果指定了自变量(预测)变量,则专家建模器为ARIMA模型中的内容选择那些与该相依序列具有统计显著关系的模型。适当时,使用差分和/或平方根或自然对数转换对模型变量进行转换,缺省情况下,专家建模器既考虑指数平滑法模型也考虑ARIMA模型,还可以将专家建模器限制为仅搜索ARIMA模型或仅搜索指数平滑法模型。另外专家建模器还可以指定自动检测离群值。
Spss专家建模器推荐的模型是简单季节性模型:
(1)
(2)
(3)
:周期长度(月度数据取12,季度数据取4)
:水平的平滑参数
:季节的平滑参数
:预测超前期期数
:第
期的预测值
根据专家建模器检验并剔除离群值后的所得结果见表2:
由上表可知,专家建模器创建出的最优模型为简单季节性模型,所得R2 = 0.986,平稳R方 = 0.698,说明模型预测效果较好。
制作残差ACF与残差PACF见图5:

Figure 5. Plot of residual ACF vs. residual PACF
图5. 残差ACF与残差PACF图
从残差的ACF和PACF图形中可以看出,所有滞后阶数的自相关系数和偏自相关系数均和0没有显著的差异。另外从上表可以看出,对残差进行Q验得到的p值为0.132,即我们无法拒绝原假设,认为残差就是白噪声序列,因此该模型能够很好地识别本例中的月平均气温数据,预测结果见图6。
从图6中可以看出,真实数据和拟合数据的时序图几乎重合,这说明该模型对原数据拟合的效果很好。另外,预测的数据依然保留了原始序列的季节效应,也这说明该模型能很好的对月平均气温数据进行预测,做出预测统计表见表3。
置信区间是指在统计学中,通过对样本统计量进行计算得到的,用以估计总体参数真实值的区间。这个区间反映了总体参数真实值具有一定概率落入该区间的程度。如中国北京2029年11月的温度预测值为6.1881℃,置信水平为95%,那我们可以认为预测值有95%的可能落在区间[−0.2809, 8.6555]内。
气候预测最终目的是进行房地产决策,所以我们通过该模型预测的数据记录中国北京,德国柏林,摩洛哥卡萨布兰卡从2024年到2029年30摄氏度及以上的月平均气温出现次数,作为这三个国家未来气候风险的评分依据,结果如下见表4:

Table 4. Basis for climate risk scoring
表4. 气候风险评分依据
3. 房地产建设决策模型
模糊数学又称Fuzzy数学,是研究和处理模糊性现象的一种数学理论和方法。模糊性数学发展的主流是在它的应用方面,由于模糊性概念已经找到了模糊集的描述方式,人们运用概念进行判断、评价、推理、决策和控制的过程也可以用模糊性数学的方法来描述。例如模糊聚类分析、模糊模式识别、模糊综合评判、模糊决策与模糊预测、模糊控制、模糊信息处理等。这些方法构成了一种模糊性系统理论,构成了一种思辨数学的雏形。
模糊综合评价法 [6] 是一种基于模糊数学的综合评价方法,它在国民经济和科学技术领域已经得到了广泛应用。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象作出一个总体的评价。
3.1. 数据整理
指标数据见表5:
3.2. 综合评判
在模糊综合评价中,因素集是指评价对象的各种影响因素所组成的集合。这些因素是影响评价对象优劣、性能、状态等方面的各种指标或属性。定义因素集U为{灾害程度,地区稳定性,建筑物等级,社区服务满意度,未来气候风险}。
在模糊综合评价中,评语集是指对评价对象可能做出的各种总的评价结果所组成的集合。定义评语集V为{中国北京,德国柏林,摩洛哥卡萨布兰卡}。
3.3. 确定隶属函数
隶属函数主要用于描述元素对模糊集合的隶属关系。由于这种关系的不分明性,隶属函数用从区间[0, 1]中所取的数值来代替0和1这两值,以表示元素属于某模糊集合的“真实程度”。
定义灾害程度的隶属函数:
(4)
定义地区稳定性的隶属函数:
(5)
定义建筑物等级隶属函数:
(6)
定义社区服务满意度隶属函数:
(7)
定义未来气候风险隶属函数:
(8)
3.4. 计算隶属度
根据各隶属函数计算出3个国家所对应的不同隶属度,见表6:
这样就确定了单因素判断矩阵:
(9)
3.5. 综合评价
根据熵权法计算的权重为:A = [0.2869, 0.0636, 0.3270, 0.0214, 0.3011],于是得到综合评价向量为:
B = A∙R (0.1705, 0.6327, 0.3905),通过分析得分可以得知:
1) 德国柏林评分最高。由此建议房地产公司把德国作为最佳的房地产投资地,因为在综合了目的地灾害程度,地区稳定性,建筑物等级,社区服务满意度,未来气候风险这五个指标后,德国高居榜首,并且五个指标的得分也比较均衡。计算结果表明德国投资风险较低,有助于减少极端天气带来的损失。德国社区发展程度也比较高,这有助于节省建设时的相关费用,也能提升房屋建设的效率自然也就会获得较高的经济效益。而德国的建筑物等级则说明:德国房屋的原材料和建造技术都是优质的,未来房地产公司可以考虑雇佣当地的工人,直接使用当地原材料进行建造,将会获取更大的收益。
2) 摩洛哥卡萨布兰卡评分属于中等水平。计算结果表明它在建筑物等级方面评分较低,未来如果考虑在此进行建设,建筑材料,建筑技术等因素是必须要重视的。其社区发展程度评分低,这可能会给房地产建设带来一些困难。它在气候风险方面的评分很高,说明摩洛哥卡萨布兰卡的气候环境比较稳定,在当地建设时,气候方面的关注度可以弹性调节。
3) 中国北京评分最低。计算结果表明其在天气方面的评分极低,建设时就要着重考虑规避气候风险的问题。但它有着较高的地区稳定性和社区服务满意度,这说明中国的营商环境是优越的,这对于投资建厂是极为有利的,说明如果在能够规避一定的天气风险,考虑在中国进行建设投资也是可观的。
4. 结论
本文能够理论联系实际,以目前房地产开发商比较关心的极端天气入手,以中国北京,德国柏林,摩洛哥卡萨布兰卡三个极具代表性的城市为例,进行投资可行性打分。本文将时间序列预测和模糊数学的理论相结合,并引入到房地产领域,为开发商面对投资决策问题提供了一个很好的解决办法。最后得出的结论可靠,有效,具有较强的理论意义和实用价值,有助于未来房地产开发商进行合理的投资决策,具有一定的创新性。
但本文在举例方面有所欠缺,应该计算出多个城市的评分进行比较分析,排除偶然因素对模型的干扰。接下来的研究需要在此方面加以改进,进一步提高模型的适用性和可操作性。