1. 引言
煤矿瓦斯爆炸会导致巷道设施被严重破坏、给煤矿带来巨大财产损失 [1] [2] [3] ,为了掌握瓦斯爆炸破坏特性,国内外许多学者对此进行了大量研究 [4] [5] [6] ,并取得丰硕的研究成果。为了优化工程结构的抗爆性能、提高系统安全度,人们提出了许多损伤理论和评估方法,这些理论和方法广泛应用于指导工程实践,并为工程结构损伤破坏研究奠定了基础。例如,2004年,Soh等 [7] 进行了大量数值模拟试算,通过曲线拟合的方式获得了构件的P-I曲线。2006年,孙建运等 [8] 研究了钢骨混凝土柱在爆炸冲击荷载作用下的响应特征,提出了钢骨混凝土柱的等效单自由度模型的等效屈服强度计算公式。2009年,李忠献等 [9] 研究了在爆炸荷载下钢筋混凝土板的破坏特性,提出了基于剩余承载力的破坏准则,建立了爆炸冲击荷载作用下钢筋混凝土柱的P-I曲线和拟合公式。2010年,蒋维等 [10] 建立了三轴压缩条件下岩石的损伤本构模型,结合试验曲线和多元函数极值条件验证了损伤本构模型参数。2011年,Mutalib等 [11] 对爆炸荷载作用下纤维增强混凝土柱的损伤评估进行了研究,以柱的剩余承载力为损伤指标,考虑了柱的尺寸、材料强度、纤维厚度及强度等参数,通过数值模拟得到了纤维增强混凝土柱的P-I曲线。2012年,吴赛 [12] 研究了不同参数对复式钢管混凝土柱抗爆能的影响,以剩余承载力作为破坏准则,建立了P-I曲线。2012年,汪维 [13] 分析了爆炸载荷形状及构件参数对各临界损伤程度P-I曲线的两条渐近线的影响,提出了构件P-I曲线的一种简化方法。2013年,汪 [14] 采用了Johnson-Cook强度模型,评估了爆炸作用下的方钢柱损伤情况,并提出了P-I-t曲面计算式。2014年,丁阳等 [15] 提出了基于钢柱抗剪承载力的失效破坏准则,获得了爆炸荷载作用下钢柱的动态响应、损伤评估和失效情况。2014年,Dragos [16] 提出了新式等效单自由度法,并获取了在爆炸荷载作用下的钢柱P-I曲线。2016年,田志敏等 [17] 试验了钢板混凝土复合梁的承载性能,得到了爆炸荷载作用下钢板混凝土复合梁的P-I曲线。2016年,陈俊杰等 [18] 基于单自由度等效体系运动方程和结构变形的理想弹塑性模型,运用图像法计算阻尼耗能,得到了P-I曲线冲量区和准静态区的渐进线方程,并得到了P-I曲线动态区的拟合公式。2016年,陈晔 [19] 模拟研究了室内爆炸波的传播以及爆炸诱发火灾发展过程,并建立了通过使用P-I曲线预测爆炸荷载与火灾联合作用下钢柱的损伤程度的方法。2017年,师吉浩等 [20] 分析了不同爆炸载荷下的三种波纹板防爆墙的动态响应,拟合了三种类型波纹板防爆墙的抗爆评估P-I曲线,获取了拟合不同防爆墙P-I曲线的统一经验方程形式。2017年,闫秋实等 [21] 利用有限元分析方法,建立了“炸药–空气–混凝土柱”耦合模型,提出了基于承载能力的损伤评估方法。2018年,潘建军等 [22] 构建了一种基于等效单自由度模型的钢管RPC柱抗爆超压–冲量(P-I)曲线,并对标准ISO-834火灾和爆炸作用后的4根钢管RPC柱进行损伤评估。
综上分析发现,有关爆炸冲击荷载对工程结构损伤破坏的研究大多体现在固体炸药爆炸方面,而且对地面设施的炸药爆炸破坏P-I评估已经比较成熟,但是对于矿井瓦斯爆炸冲击荷载对巷道壁面结构破坏的P-I评估的研究十分有限。大量实验和数值模拟表明 [23] [24] [25] ,对矿井巷道破坏进行评估,P-I曲线也可以作为一个很好的方法。因此,本文在分析P-I曲线基本理论基础上,以支座转角作为损伤破坏指标判定巷道壁面损伤破坏等级,并应用此方法评估不同瓦斯爆炸强度下的巷道损伤破坏程度。研究结果不但能为不同爆炸强度下的巷道损伤破坏提供防护依据,而且能根据评估结果分析巷道在瓦斯爆炸荷载后的安全性及使用价值。
2. 巷道壁面损伤破坏准则和评估方法
2.1. 壁面破坏准则
常见的爆炸冲击波对物体的伤害评估准则有:超压准则、冲量准则和超压–冲量准则。超压准则:若目标物的损伤破坏主要由超压峰值造成的,则适合采用超压准则。当物体在爆炸持续较小超压下发展破坏,则不适应于单独使用超压准则评估损伤。冲量准则:冲量破坏准则认为爆炸冲击波对受载物造成损伤破坏,取决于爆炸冲量大小。如果冲量值越过损伤破坏临界值,则受载物损伤破坏;但超压峰值也有高低,当超压很小即使荷载持时再长目标也不会产生任何损伤破坏,故仅用冲量准则也是不全面的。冲量准则的适用目标通常达到损伤破坏需要经历比较长的时间。超压–冲量准则:超压–冲量准则综合考虑了超压准则和冲量准则的优缺点,该准则认为在超压和冲量共同满足某一临界条件时,受载物就会产生损伤破坏。超压–冲量(P-I)准则适合于爆炸荷载下大多数目标物的损伤破坏评估,同时考虑超压和冲量两个重要的爆炸参数。所以本次对瓦斯爆炸冲击载荷下巷道壁面的损伤破坏评估采用超压–冲量准则,即P-I准则。
2.2. 壁面损伤评估方法
常见的爆炸冲击波对物体的损伤评估方法有支座转角损伤评估、剪切滑移量损伤评估、剩余承载力损伤评估和基于延性比的损伤评估等 [26] [27] 。
1)支座转角损伤评估
壁面损伤破坏程度常和壁面最大动态响应相关联,常用评估参数支座转角来评估壁面损伤破坏程度 [26] [27] ,支座转角大小来源于壁面单元的位移,位移大小在爆炸试验的现场容易测量,在数值模拟单元上也方便提取,在抗爆设计标准中更容易于查找。
支座转角θ定义见图1,表达式为:
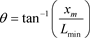 (1)
(1)
θ为支座转角,xm为变形位移量,Lmin是峰值位移点距最近支座的距离,等于单元长度的一半,支座转角与最大弯矩处横截面转角相关。在张拉膜动态响应中,θ随着峰值位移与长度的比。
可以通过对不同瓦斯爆炸强度下巷道壁面的损伤破坏程度进行粗略评估,并选择支座转角θ的P-I准则来评估巷道壁面损伤破坏程度,损伤破坏等级和相关参数如表1所示。
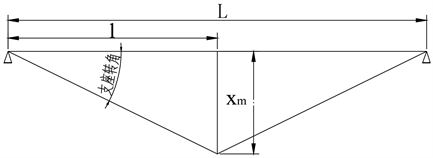
Figure 1. Schematic diagram of bearing angle
图1. 支座转角示意图

Table 1. Criteria for damage assessment
表1. 损伤破坏评估等级
2)剪切滑移量损伤评估
巷道壁面单元的剪切滑移量可以表示为:
(2)
其中,Ws是剪切滑移量,表示单元剪切变形累积的滑移大小,S是剪应变平均值,L是单元长度。
3)剩余承载力损伤评估
通过壁面煤岩体承载能力作为损伤破坏指标来评定巷道壁面的损伤破坏程度,具有现实意义。剩余承载力损伤破坏参数如下:
(3)
其中,W是剩余承载力,r是壁面单元剩余承载力,R是壁面单元基准极限弯矩。
4)基于延性比的损伤评估
延性比Q对评估延性物体的低等级损伤破坏和脆性物体的所有等级损伤破坏较为适宜。称单元的挠度与屈服挠度的比为延性比:
(4)
其中,Q是延性比,E是单元的屈服挠度,S是单元的最大位移。
通过分析以上4种损伤评估参数指标,发现损伤评估参数指标既有差别性(例如:由于定义划分标准不太相同,各损伤评估参数有所区别),也有一致性(例如:损伤等级和防护等级关联密切)。基于巷道壁面破坏特性及ANSYS/LS-DYNA特性,结合P-I评估办法,本次选择支座转角作为损伤评估参数。
3. 壁面损伤破坏评定
为建立巷道壁面的P-I损伤评估曲线,本次利用瓦斯爆炸冲击荷载作用下巷道壁面的动态响应数值模拟数据(由于篇幅限制,数据见附件),并根据表1中的损伤评估准则,经过多次模拟获得了一系列不同损伤程度区间边界点,将这些边界点连结成P-I曲线,并通过origin进行曲线的公式拟合。P-I曲线上的每一个点对应着特定的支座转角,也与特定损伤等级相关联,并且是在具体的瓦斯爆炸荷载下得到的。经过大量的反复试算,得到各损伤破坏等级的分界点,将各测点对应的超压和冲量标注在P-I空间内,如图2所示。
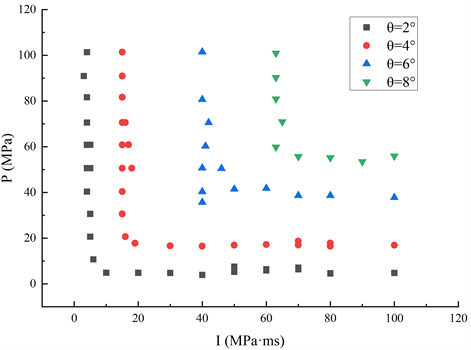
Figure 2. Measuring value of dividing point
图2. 分界点测值
通过origin拟合得到的P-I曲线如图3所示。图中4条P-I曲线分别是θ = 2˚、θ = 4˚、θ = 6˚和θ = 8˚的损伤破坏程度临界值,将P-I空间划分为5个区域,分别为轻度损伤区、中度损伤区、重度损伤区,严重损伤区、坍塌破坏区,损伤程度划分如表2所示。
图3中每一个组合点表示一种瓦斯爆炸强度下的巷道壁面测点损伤情况,通过曲线拟合得到的P-I曲线通常可以表示为:
(5)
其中,P0为极限超压,I0为极限冲量,即图3中超压渐近线和冲量渐近线所对应的数值。对于巷道壁面,各参数取值如表3所示。
因此,曲线拟合公式可表达为:
(6)
将得到的P-I损伤破坏曲线用于不同瓦斯爆炸强度下的巷道损伤破坏程度评估,不同爆炸强度(即P-I组合)下封闭端壁面41605号测点位移响应如图4所示,由爆炸产生的最大位移量可对壁面损伤破坏进行等级评估。
当巷道内瓦斯爆炸强度为1.7E06J时,数值模拟得到巷道壁面单元测点上的最大超压值为3.45 MPa,最大冲量值为3.91 MPa·ms,同时测得测点最大位移为0.00085 m,经计算得到支座转角为1.95˚。将超压测值–冲量测值的组合点绘制在图3的P-I曲线图中,得到的损伤破坏程度为轻度损伤。
当巷道内瓦斯爆炸强度为5.1E06J,数值模拟得到巷道壁面单元测点上的最大超压值为10.4 MPa,最大冲量值为11.9 MPa·ms,同时测得测点最大位移为0.00149 m,经计算得到支座转角为3.41˚。将超压测值和冲量测值的组合点绘制在图3的P-I曲线图中,得到的损伤破坏程度为中度损伤破坏。
当巷道内瓦斯爆炸强度增加到17E06J时,数值模拟得到巷道壁面单元测点上的最大超压值为27.6 MPa,最大冲量值为31.7 MPa·ms,同时测得测点最大位移为0.00243 m,经计算得到支座转角为5.55˚。将超压测值和冲量测值的组合点绘制在图3的P-I曲线图中,得到的损伤破坏程度为重度损伤破坏。
当巷道内瓦斯爆炸强度为20E06J时,数值模拟得到巷道壁面单元测点上的最大超压值为55.2 MPa,最大冲量值为63.5 MPa·ms,同时测得测点最大位移为0.00342 m,经计算得到支座转角为7.78˚。将超压测值和冲量测值的组合点绘制在图3的P-I曲线图中,得到的损伤破坏程度为严重损伤破坏。

Figure 4. The displacement of different explosion
图4. 不同爆炸强度时的位移
当巷道内瓦斯爆炸强度为34E06J时,数值模拟得到巷道壁面单元测点上的最大超压值为68.9 MPa,最大冲量值为79.4 MPa·ms,同时测得测点最大位移为0.0038 m,经计算得到支座转角为8.64˚。将超压测值和冲量测值的组合点绘制在图3的P-I曲线图中,得到的损伤破坏程度为坍塌破坏。5组数值模拟动态响应与P-I曲线评估结果基本一致。
4. 结论
1) 基于爆炸冲击荷载作用下巷道壁面的动态响应数值模拟数据,选取支座转角为巷道壁面损伤破坏评估参数,以P-I为损伤破坏评估准则,获得不同损伤等级区间边界点,将连结边界点成P-I曲线,并获得了曲线的拟合公式。
2) 建立了以支座转角2˚,4˚,6˚和8˚为节点的轻度损伤,中度损伤,重度损伤,严重损伤和坍塌破坏区域。
基金项目
国家自然科学基金项目“矿井多爆源瓦斯爆炸传播特性及热冲击动力学机制研究”(编号:52174178)、“矿井瓦斯爆炸能量释放转化特性及热冲击能量损耗研究”(编号:52174177)。