双星S_2,6的平面Turán型问题的一个上界

An Upper Bound for the Planar Turán Type Problem of Double Star S_2,6

摘要: 极值图论是图论中的重要内容，主要研究具有某些性质的图的极值问题。平面图的Turán数是指具有n个顶点的平面图G的最大边数，其中图G不包含H作为一个子图。这个问题是由Dowden在2016年提出的。最近Ghosh等人研究了若干双星图的平面Turán数，并得到很多结果。在这里，我们将给出不含双星S_2,6且任意相邻两点度数之和不等于12的平面图边数的上界，即设图G是个顶点的平面图，图中不包含S_2,6作为子图且任意相邻两点度数之和不等于12，那么有。

Abstract: Extremal graph theory is an important part of graph theory, which aims to study the extremal structure of graphs with certain properties. The planar Turán number, denoted by , is the maximum number of edges in graph G on n vertices, where G does not contain H as a subgraph. This problem was initiated by Dowden in 2016. Recently, Ghosh et al. discussed the planar Turán numbers of several double stars and obtained many results. In this paper, we will give the upper bound for the number of edges in the planar graph in which there does not exist a double star S_2,6 and degree sum of adjacent vertices is not equal to 12. That is, if the graph G is a plane diagram of vertices, and the graph does not contain S_2,6 as a subgraph, and the sum of the degrees of any adjacent two points is not equal to 12, then .

1. 前言

图论是组合数学的一个分支，是离散数学的重要组成部分。极值图论是图论的一个分支，是由Mantel [1] 在1907年提出来的，平面Turán问题是Turán问题中的一种，研究的对象从一般图缩减到平面图，所谓平面图是指可以画在平面上并且不同的边可以互不相交的图。例如，在图、圈、Theta图、路、匹配等上进行一系列的Turán数的研究，图里面包括一些单图，例如星图。近几年来平面图的Turán数研究也越来越多，与平面Turán数问题相关的更多文献可以参看 [2] - [8] 。

对于星的平面Turán数的研究，Lan [9] 几乎已经完全解决了当 $n\ge t+1$ 时， $e{x}_p\left(n,K_{1,t}\right)$ 的数值问题，随后又在文献 [10] 中相继求出了 $t\ge 3$ ， $n\ge t+2$ ， $e{x}_p\left(n,K_{2,t}\right)$ 的确切值。星的平面Turán数可以帮助我们更好地理解和研究平面图的性质和特征。星的平面Turán数的研究对于理解和应用平面图具有重要的意义。关于星图的更多信息可以参考文献 [11] 。

Ghosh [11] 进一步地研究了双星的平面Turán数。一个(k, l)双星，记作S_k,l，是指由一条边uv通过额外连接k个和l个顶点所形成的图。Ghosh等人给出了当 $n\ge 16$ 时， $e{x}_p\left(n,S_{2,2}\right)=2n-4$ ；当 $n\ge 1$ 时， $e{x}_p\left(n,S_{2,3}\right)=2n$ 。并且计算出了 $e{x}_p\left(n,S_{2,4}\right)$ ， $e{x}_p\left(n,S_{2,5}\right)$ ， $e{x}_p\left(n,S_{3,3}\right)$ ， $e{x}_p\left(n,S_{3,4}\right)$ 的上下界。在本文中我们给出了不含双星图S_2,6且6度点互不相邻的平面图边数的上界，对n进行归纳完成了证明，得到了结果 $e{x}_p\left(n,S_{2,6}\right)\le \frac{23}{8}n-3$ 。

为了方便叙述本文的主要结论，下面我们介绍所需要用到的定义和符号。给定一个无向图 $G=\left(V,E\right)$ ，其中V是图G的顶点集，E是图G的边集，分别用 $d_G\left(v\right)$ 、 $\Delta \left(G\right)=max\left\{d_G\left(x\right):x\in V\left(G\right)\right\}$ 、 $\delta \left(G\right)=\min \left\{d_G\left(x\right):x\in V\left(G\right)\right\}$ 表示顶点v的度数、图G的最大度和最小度。设 $n_k$ 是度为k的顶点数。此外，我们用 $N_G\left[v\right]$ 来表示G中与v相邻的顶点的集合。让 $N_G\left[v\right]=N_G\left(v\right)\cup \left\{v\right\}$ ，对于任意子集 $S\subset V\left(G\right)$ ，在S上导出的子图记为 $G\left[S\right]$ 。我们用 $G\backslash S$ 来表示 $V\left(G\right)\backslash S$ 上的诱导子图，如果 $S=\left\{v\right\}$ ，我们简单地写 $G\backslash v$ 。我们用 $e\left[S,T\right]$ 来表示S和T之间的边数，其中S，T是 $V\left(G\right)$ 的子集。 $k-l$ 边是这样一条边，其端点的顶点度分别为m和n，并且 $k-l-s$ 路是一条由顶点度分别为k，l，s的三个顶点组成的路。

2. 主要结论

下面我们给出主要结论，并通过对n的归纳完成证明。

定理2.1 设图G是 $n\ge 2$ 个顶点的平面图，图中不包含S_2,6作为子图且任意相邻两点度数之和不等于12，则

$e\left(G\right)\le \frac{23}{8}n-3.$

证明：

首先我们讨论顶点数较少的情形。

断言1. 对于 $2\le n\le 24$ ， $e\left(G\right)\le \frac{23}{8}n-3$ 。

易知当 $n=2$ 时结论成立。我们有 $n\ge 3$ 个顶点极大平面图其最大边数为 $3n-6$ 。而当 $n\le 24$ 时， $3n-6\le \frac{23}{8}n-3$ 。 □

为了后续讨论方便，由断言1我们不妨假设 $n\ge 24$ 。

断言2. 如果图G中存在顶点u满足 $d\left(u\right)\le 2$ ，则 $e\left(G\right)\le \frac{23}{8}n-3$ 。

不妨删除这一顶点u，则根据归纳假设可知，剩余图的边数 $e\left(G\backslash u\right)\le \frac{23}{8}\left(n-1\right)-3$ 。那么 $e\left(G\right)=e\left(G\backslash u\right)+d\left(u\right)\le \frac{23}{8}\left(n-1\right)-3+2\le \frac{23}{8}n-3$ 。 □

断言3. 如果图G中存在边割集 $E\left[S_1,S_2\right]$ 满足 $e\left[S_1,S_2\right]\le 3$ ， $\left|S_1\right|,\left|S_2\right|\ge 2$ ，则 $e\left(G\right)\le \frac{23}{8}n-3$ 。

假设图G中存在边割集 $E\left[S_1,S_2\right]$ ，其中 $V\left(G\right)=S_1\cup S_2$ 。根据条件可知， $e\left[S_1,S_2\right]\le 3$ 。易知子图 $G\left[S_1\right],G\left[S_2\right]$ 中也不存在S_2,6，由断言1和归纳假设可知 $e\left(G\left[S_1\right]\right)\le \frac{23}{8}\left|S_1\right|-3$ ， $e\left(G\left[S_2\right]\right)\le \frac{23}{8}\left|S_2\right|-3$ 。那么

$\begin{array}{c}e\left(G\right)=e\left(G\left[S_1\right]\right)+e\left(G\left[S_2\right]\right)+e\left[S_1,S_2\right]\\ \le \frac{23}{8}\left|S_1\right|-3+\frac{23}{8}\left|S_2\right|-3+3\\ =\frac{23}{8}n-3.\end{array}$

□

同理可证当图G的边连通度 $\lambda \left(G\right)\le 2$ 时， $e\left(G\right)\le \frac{23}{8}n-3$ 。下面不妨设图G的边连通度 $\lambda \left(G\right)\ge 3$ 。我们进一步讨论图G的最大度的取值情况。

断言4. 图G的最大度满足 $\Delta \left(G\right)\le 7$ 。

如果G中包含一个顶点 $v\in V\left(G\right)$ ，满足 $d\left(v\right)\ge 9$ 。注意到对每个 $u\in N\left(v\right)$ ，我们有 $d\left(u\right)\ge 3$ 。易知图G中存在一个S_2,6作为子图。

进一步地，我们分析当图中存在度数为8的顶点时，图G的边数满足不等式。设图中存在点 $v\in V\left(G\right)$ ，使得 $d\left(v\right)=8$ ，令 $S=N\left(v\right)\cup \left\{v\right\}$ 。很容易知道对于每个 $u\in N\left(v\right)$ ，如果u和 $V\left(G\right)\backslash S$ 中任一顶点相邻，那么 $d\left(u\right)=2$ 。否则，我们会在G中找到一个S_2,6。而这与条件 $\delta \left(G\right)\ge 3$ 矛盾，因此v的所有邻居顶点均不与 $V\left(G\right)\backslash S$ 中的点邻接，这意味着 $G\left[S\right]$ 是一个独立的连通分支。又根据边连通度 $\lambda \left(G\right)\ge 3$ ，可知 $V\left(G\right)=S$ 。也就是说图G的顶点个数恰好为9，与假设 $n\ge 24$ 矛盾。 □

通过上述讨论，我们得到图G中顶点度的取值范围，即 $\delta \left(G\right)\ge 3$ 和 $\Delta \left(G\right)\le 7$ 。

根据双星图S_2,6的特点，度数为7的顶点存在生成双星图的可能，下面我们分别详细讨论7-7边、7-6边这两种图中的子结构。

断言5. 如果G包含7-7边这种子图结构，那么有 $e\left(G\right)\le \frac{23}{8}n-3$ 。

假设uv是一条7-7边，由于G不包含S_2,6，所以uv上至少有5个三角形，我们根据uv边上的三角形数目来区分为两种情形。

情形1. 边uv上有6个三角形的公共边

设a，b，c，d，e和f是与u和v相邻的顶点，如图1所示。设 $S=\left\{u,v,a,b,c,d,e,f\right\}$ ， $S_1=\left\{a,b,c,d,e,f\right\}$ 和 $H=G\left[S\right]$ 。我们下面计算与这一子图结构关联的边的数目，首先S₁中的所有顶点都可以形成一条长度至多为5的路径；其次S₁中的每个顶点最多在 $V\left(G\right)\backslash S$ 中有一个邻居，否则图中可以找到S_2,6。但是我们注意到，若S₁中顶点都存在向 $V\left(G\right)\backslash S$ 中点连接的边，则图中存在大小至多为2的边割集，与 $\lambda \left(G\right)\ge 3$ 矛盾，因此S₁与 $V\left(G\right)\backslash S$ 之间不存在边。

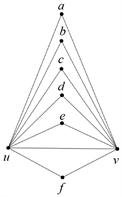
Figure 1. Subgraph structure with 7-7 sides and 6 triangles

图1. 有7-7边并且有6个三角形的子图结构

若我们删除H中的顶点，同时删去的边数最多为13 + 5 = 18条，根据归纳假设，我们有

$\begin{array}{c}e\left(G\right)\le e\left(G\backslash H\right)+18\\ \le \frac{23}{8}\left(n-8\right)-3+18\\ \le \frac{23}{8}n-3.\end{array}$

情形2. 边uv上有5个三角形的公共边

设a，b，c，d和e均与u和v相邻，f与u相邻但不与v相邻，g与v相邻而不与u相邻，令 $S_1=\left\{a,b,c,d,e\right\}$ 、 $S=\left\{u,v,f,g\right\}\cup S_1$ 和 $H=G\left[S\right]$ ，子图结构如图2所示。

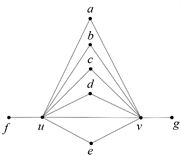
Figure 2. Subgraph structure with 7-7 sides and 6 triangles

图2. 有7-7边并且有6个三角形的子图结构

同样的，我们计算与这一子图结构关联的边的数目，首先S₁中的所有顶点都可以形成一条长度至多为4的路；其次S₁中的每个顶点至多在 $V\left(G\right)\backslash S$ 中有一个邻居，否则图中可以找到S_2,6；再次顶点f，g最多在 $V\left(G\right)\backslash S$ 中有一个邻点，否则也存在S_2,6；最后f，g与S₁中顶点也可能相连，且f，g两点可能相邻。

这里我们注意到，如果f，g在平面图的不同面内，考虑到任意边割集 $E\left[S_1,S_2\right]$ 其中 $\left|S_1\right|,\left|S_2\right|\ge 2$ ，满足 $e\left[S_1,S_2\right]\ge 4$ ，比如f在这种情况下只能与a，e拥有在 $V\left(G\right)\backslash S$ 中度为3的公共邻点。这意味着图G的顶点数至多为11，则由断言1可知结论成立。因此f，g在同一面中。特别地，如果fg是一条边，则顶点f，g与 $V\left(G\right)\backslash S$ 之间均不再存在边。

因此若我们删除H中的顶点，此时删去的边数最多为13 + 4 + 2 + 2 + 4 = 25条，根据归纳假设，我们有

$\begin{array}{c}e\left(G\right)\le e\left(G\backslash H\right)+25\\ \le \frac{23}{8}\left(n-9\right)-3+25\\ \le \frac{23}{8}n-3.\end{array}$

□

断言6. 如果G包含7-6边这种子图结构，那么有 $e\left(G\right)\le \frac{23}{8}n-3$ 。

假设uv是一条7-6边，由于G不包含S_2,6，所以uv上至少有4个三角形，我们根据uv边上的三角形数目来区分为两种情形。

情形1. 边uv上有5个三角形的公共边

设a，b，c，d，e是与u和v相邻的顶点，f是只与u相邻的顶点，如图3所示。

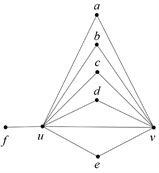
Figure 3. Subgraph structure with 7-6 sides and 5 triangles

图3. 有7-6边并且有5个三角形的子图结构

设 $S=\left\{u,v,a,b,c,d,e,f\right\}$ ， $S_1=\left\{a,b,c,d,e\right\}$ 和 $H=G\left[S\right]$ 。类似地，我们计算与这一子图结构关联的边的数目，首先S₁中的所有顶点都可以形成一条长度至多为4的路；其次S₁中的每个顶点至多在 $V\left(G\right)\backslash S$ 中有一个邻居，否则图中可以找到S_2,6；再次顶点 f最多在 $V\left(G\right)\backslash S$ 中有一个邻点，否则也存在S_2,6；最后f与S₁中顶点也可能相连。

进一步地，a，b，c，d，e中至少有3个点与 $V\left(G\right)\backslash S$ 之间不存在边。如若不然，则图中必然存在大小至多为2的边割集，与 $\lambda \left(G\right)\ge 3$ 矛盾。

若我们删除H中的顶点，同时删去的边最多为12 + 4 + 2 + 3 = 21条，根据归纳假设，我们有

$\begin{array}{c}e\left(G\right)\le e\left(G\backslash H\right)+21\\ \le \frac{23}{8}\left(n-8\right)-3+21\\ \le \frac{23}{8}n-3.\end{array}$

情形2. 边uv上有4个三角形的公共边

设a，b，c，d，e是与u和v相邻的顶点，f是只与u相邻的顶点，g是只与v相邻的顶点，如图4所示。

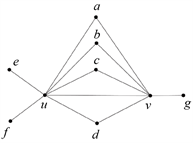
Figure 4. Subgraph structure with 7-6 sides and 4 triangles

图4. 有7-6边并且有4个三角形的子图结构

设 $S=\left\{u,v,a,b,c,d,e,f,g\right\}$ ， $S_1=\left\{a,b,c,d\right\}$ 和 $H=G\left[S\right]$ 。我们计算与这一子图结构关联的边的数目，首先S₁中的所有顶点都可以形成一条长度至多为3的路；其次S₁中的每个顶点至多在 $V\left(G\right)\backslash S$ 中有一个邻居，否则图中可以找到S_2,6；再次顶点e，f至多在 $V\left(G\right)\backslash S$ 中有一个邻点，否则存在S_2,6；而顶点g至多在 $V\left(G\right)\backslash S$ 中有4个邻点，否则也存在6-6边或S_2,6；最后e，f，g与S₁中顶点也可能相连，三个顶点e，f，g可能彼此相连。

与之前讨论类似，如果e，g之间有边相连，则e与 $V\left(G\right)\backslash S$ 之间均不再存在边，g向外连接的边数也要减1。下面我们从图G中删除H中的顶点，当e，f处于相同的面内时，删除的边数至多为12 + 3 + 2 + 2 + 5 + 1 = 25。

则根据归纳假设，我们有

$\begin{array}{c}e\left(G\right)\le e\left(G\backslash H\right)+25\\ \le \frac{23}{8}\left(n-9\right)-3+25\\ \le \frac{23}{8}n-3.\end{array}$

当e，f处于平面图中不同的面时，不妨设e单独在一个面内，且面边界点上有c，d。此时如果e存在向外连接的边，则c，d，e将连接 $V\left(G\right)\backslash S$ 中度为3的顶点，否则其中存在每个部分顶点数都大于1的3边割。此时将这一顶点加入集合S进行下一步计算，讨论同上；如果e没有向外连接的边，则c，d也不存在向外连接的边，同样可以讨论删除的边数情况。

综合上述情况，删除的总边数至多为25，由归纳假设结论成立。 □

任意取相邻两点 $x,y\in V\left(G\right)$ ，由图G中任意相邻两点度数之和不等于12，结合上述的断言，最后只需要讨论 $d\left(x\right)+d\left(y\right)\le 11$ 的情形，对G所有的边求和，我们有

$\begin{array}{c}11\cdot e\ge {\displaystyle {\sum }_{xy\in E\left(G\right)}\left(d\left(x\right)+d\left(y\right)\right)}\\ ={\displaystyle {\sum }_{x\in V\left(G\right)}{\left(d\left(x\right)\right)}^2}\\ \ge n{\bar{d}}^2=n{\left(\frac{2e}{n}\right)}^2\end{array}$

其中 $\bar{d}$ 是G的平均度。

由上式可得，当 $n\ge 24$ 时， $e\left(G\right)\le \frac{11}{4}n\le \frac{23}{8}n-3$ 。

因此对于 $n\ge 1$ ，我们有 $e\left(G\right)\le \frac{23}{8}n-3$ ，证毕。

3. 总结

本文在Ghosh部分结果的基础上讨论了图中6度顶点互不相邻且不包含S_2,6作为子图的平面图的最大边数，给出了相应的上界。同时我们注意到可以通过下述方式构造 $e{x}_p\left(n,S_{2,6}\right)$ 的下界。因为S_2,6包含10个顶点，所以 $n\le \text{9}$ 的最大平面图不包含S_2,6。令 $9|n$ 。考虑由9个顶点上的最大平面图的 $\frac{n}{9}$ 个不相交的图组成的平面图，这些平面图不包含S_2,6。因此， $e{x}_p\left(n,S_{2,6}\right)\ge \frac{21}{9}n$ 。这都为后续的研究打下了坚实的基础。