欠驱动垂直起降飞行器解耦反演跟踪控制

Decoupling Inversion Tracking Control of Underactuated Vertical Takeoff and Landing Aircraft

摘要: 针对欠驱动垂直起降飞行器这种典型的强耦合非线性系统的跟踪问题，引入坐标变换和输入变换，把原模型变为一种方便控制器设计和稳定性分析的形式，变换后的模型可以分解为一个线性可控子系统和一个低阶的非线性系统，对于非线性系统，采用反演法设计输出反馈控制律，确保系统可以渐近收敛于预定轨迹。这种方法同已有的方法比较，简单直观，仿真结果表明，飞行器的实际轨迹和实际速度可以较好地收敛到预定的轨迹和速度。

Abstract: For the tracking problem of a typical strongly coupled nonlinear system, underactuated vertical takeoff and landing aircraft, coordinate transformation and input transformation are introduced to transform the original model into a convenient form for controller design and stability analysis. The transformed model can be decomposed into a linear controllable subsystem and a low order nonlinear system. For the nonlinear system, the inversion method is used to design the output feedback control law, ensuring that the system can asymptotically converge to the pre controller fixed trajectory. Compared with existing methods, this method is simple and intuitive. Simulation results show that the actual trajectory and speed of the aircraft can converge well to the predetermined trajectory and speed.

1. 引言

欠驱动系统是指用较少的输入控制机械系统较多的自由度，这种控制问题一般属于本质非线性控制系统的范畴，随着科技的发展，欠驱动系统的应用领域日趋广泛，如水下机器人、船舶、卫星、垂直起降飞行器(VTOL)等。VTOL主要指轰炸机或战斗机，一般具有推动和滚动两个控制输入，三个输出的欠驱动系统。由于它可以自由起降，不受跑道的限制，在军用和民用两方面都有重要的价值，近年来引起了人们极大的研究兴趣。VTOL的控制难点在于这是一个欠驱动、强耦合的非线性系统。早期的研究者多是通过输入输出非线性反馈线性化的方法研究系统的位姿、稳定性和轨迹跟踪问题 [1] [2] [3] [4] 。但在设计控制器时，没有考虑滚动输入和横向控制两者的耦合作用，这些耦合作用是客观存在的。随后的研究者注意到了耦合因素，并引入坐标变换，采用李雅谱诺夫方法设计控制器，使系统可以有较好的渐近稳定性。文献 [5] 通过坐标变换将三个二阶系统解耦，设计了全局渐近稳定跟踪器。文献 [6] 研究了不确定有界扰动条件下系统的稳定问题。文献 [7] [8] [9] 利用kaerman滤波方法，设计了一种非线性反馈控制律，补偿 VTOL的未建模动态并提升系统的鲁棒性。文献 [10] 针对外部扰动的提出了一种神经网络跟踪算法，这些都为本文开展工作打下了好的基础，但目前VTOL的输出反馈跟踪控制问题仍然没有很好地解决，鉴于此，本文通过引入坐标输入变换解耦，把VTOL的动力学模型变为二阶的链式系统，利用反演法设计输出反馈控制律，保证系统渐近收敛于参考轨迹。本文较之于文献 [5] ，控制器的设计更为直观，方法更为简便，而且可以更好地渐近收敛于参考轨迹。

本文的结构安排如下：第一部分介绍了VTOL机器人的控制方法并提出了自己的设计思路。第二部分建立了数学模型，第三部分对控制器的设计思路进行了介绍。第四部分对所设计的控制器的稳定性进行了分析。第五部分进行了matlab仿真实验。第六部分进行了总结讨论。

2. VTOL的动力学建模

图1为垂直起降飞行器的飞行悬停示意图。为了使问题得到简化，VTOL的空中运动可以简化为xy面内的运动，我们主要关注飞行器的质心位置 $x\left(t\right),y\left(t\right)$ 和偏航角 $\theta \left(t\right)$ ，控制输入为飞行器的底部推力 ${\tau }_1$ 和滚动转矩 ${\tau }_2$ 。显然，这是一个2输入3输出的欠驱动控制系统，其动力模型可用下式描述：

$\{\begin{array}{l}\ddot{x}=-{\tau }_1\sin \alpha +\rho {\tau }_2\cos \alpha \\ \ddot{y}={\tau }_1\cos \alpha +\rho {\tau }_2\sin \alpha -g\\ \ddot{\alpha }={\tau }_2\end{array}$ ①

其中，g为重力加速度， $\rho$ 为反映两个输入之间耦合关系的相关系数， $\rho >0$ 表示施加向左滚动的正力矩，形成向右的加速度； $\rho <0$ 时结果相反。以前的控制问题总是假设 $\rho =0$ 或者比较小，本文对 $\rho$ 的取值不做限制。

Figure 1. Hover diagram of a vertical take-off and landing aircraft

图1. 垂直起降飞行器的悬停示意图

3. 动力学模型的解耦

由于各状态变量之间的耦合作用，根据原动力学模型设计控制器难度较大，为此引入非奇异的坐标变换，把原动力学模型变为一种便于设计控制器和稳定性分析的模型。解耦步骤如下：

1) 由①式的前两式，可知

$\left(\begin{array}{c}\ddot{x}\\ \ddot{y}\end{array}\right)=\left(\begin{array}{cc}-\sin \alpha & \cos \alpha \\ \cos \alpha & \sin \alpha \end{array}\right)\left(\begin{array}{c}{\tau }_1\\ \rho {\tau }_2\end{array}\right)+\left(\begin{array}{c}0\\ -g\end{array}\right)$

令

$\left(\begin{array}{c}{\tau }_1\\ \rho {\tau }_2\end{array}\right)={\left(\begin{array}{cc}-\sin \alpha & \cos \alpha \\ \cos \alpha & \sin \alpha \end{array}\right)}^{-1}\left(\begin{array}{c}{\omega }_1\\ {\omega }_2+g\end{array}\right)$

则

$\left(\begin{array}{c}\ddot{x}\\ \ddot{y}\end{array}\right)=\left(\begin{array}{cc}-\sin \alpha & \cos \alpha \\ \cos \alpha & \sin \alpha \end{array}\right){\left(\begin{array}{cc}-\sin \alpha & \cos \alpha \\ \cos \alpha & \sin \alpha \end{array}\right)}^{-1}\left(\begin{array}{c}{\omega }_1\\ {\omega }_2+g\end{array}\right)+\left(\begin{array}{c}0\\ -g\end{array}\right)=\left(\begin{array}{c}{\omega }_1\\ {\omega }_2\end{array}\right)$

$\rho {\tau }_2={\omega }_1\cos \alpha +\left({\omega }_2+g\right)\sin \alpha$

上式中， ${\omega }_1,{\omega }_2$ 为待设计的新控制量，整理上式，则动力学模型为：

$\{\begin{array}{l}\ddot{x}={\omega }_1\\ \ddot{y}={\omega }_2\\ \ddot{\alpha }=\frac{1}{\rho }\left({\omega }_1\cos \alpha +\left({\omega }_2+g\right)\sin \alpha \right)\end{array}$ ②

这样， ${\ddot{x}}_1,{\ddot{x}}_2$ 的控制耦合被消除。

针对②式，可令

$\{\begin{array}{l}x=m+\rho \sin \alpha \\ y=n-\rho \cos \alpha \\ {\omega }_1=\rho t\cos \alpha +\left(s-\rho {\stackrel{\dot{}}{\alpha }}^2\right)\sin \alpha \\ {\omega }_2=\rho t\sin \alpha -\left(t-\rho {\stackrel{\dot{}}{\alpha }}^2\right)-g\end{array}$

则

$\{\begin{array}{l}\ddot{m}=\ddot{x}-\rho {\left(\sin \alpha \right)}^{\prime \text{}\prime }\\ \ddot{n}=\ddot{y}+\rho {\left(\cos \alpha \right)}^{\prime \text{}\prime }\\ \ddot{\alpha }=\frac{1}{\rho }\left\{\cos \alpha \left(\left(s-\rho {\stackrel{\dot{}}{\alpha }}^2\right)\sin \alpha +\rho t\cos \alpha \right)+\left[\left(\rho t\sin \alpha -\left(t-\rho {\stackrel{\dot{}}{\alpha }}^2\right)-g\right)+g\right]\sin \alpha \right\}\end{array}$

整理以上结果，可得：

$\{\begin{array}{l}\begin{array}{l}\ddot{m}=s\cdot \sin \alpha \hfill \\ \ddot{n}=-\left(s\cdot \cos \alpha +g\right)\hfill \end{array}\hfill \\ \ddot{\alpha }=t\hfill \end{array}$ ③

这样，实现 ${\omega }_1,{\omega }_2$ 的解耦。

2) 为消除③中 $\sin \alpha$ 和 $\cos \alpha$ 的耦合，再次令 $s\cdot \cos \alpha =f_1$ ， $\text{tg}\alpha =r$ ， $\ddot{r}=f_2$ ， $f_1,f_2$ 为新控制量。则③式变为令

$P={\left(p_1,p_2,p_3,p_4,p_5,p_6\right)}^{\text{T}}$ 且 $p_1=n$ ， $p_2=\stackrel{\dot{}}{n}$ ， $p_3=m$ ， $p_4=\stackrel{\dot{}}{m}$ ， $p_5=r$ ， $p_6=\stackrel{\dot{}}{r}$ ，

则最后的解耦形式为：

$\{\begin{array}{l}\begin{array}{l}{\stackrel{\dot{}}{p}}_1=p_2\hfill \\ {\stackrel{\dot{}}{p}}_2=-f_1-g\hfill \end{array}\hfill \\ \begin{array}{l}{\stackrel{\dot{}}{p}}_3=p_4\hfill \\ {\stackrel{\dot{}}{p}}_4=p_5{f}_1\hfill \end{array}\hfill \\ \begin{array}{c}{\stackrel{\dot{}}{p}}_5=p_6\\ {\stackrel{\dot{}}{p}}_6=f_2\end{array}\hfill \end{array}$

4. 轨迹跟踪控制器设计

设参考跟踪轨迹为 $P_d={\left(p_{1d},p_{2d},p_{3d},p_{4d},p_{5d},p_{6d}\right)}^{\text{T}}$ ，且满足：

$\{\begin{array}{l}\begin{array}{l}{\stackrel{\dot{}}{p}}_{1d}=p_{2d}\hfill \\ {\stackrel{\dot{}}{p}}_{2d}=-f_{1d}-g\hfill \end{array}\hfill \\ \begin{array}{l}{\stackrel{\dot{}}{p}}_{3d}=p_{4d}\hfill \\ {\stackrel{\dot{}}{p}}_{4d}=p_{5d}{f}_{1d}\hfill \end{array}\hfill \\ \begin{array}{c}{\stackrel{\dot{}}{p}}_{5d}=p_{6d}\\ {\stackrel{\dot{}}{p}}_{6d}=f_{2d}\end{array}\hfill \end{array}$

$f_{1d},f_{2d}$ 为时变的参考控制输入，跟踪过程产生的误差计为： $e={\left(e_1,e_2,e_3,e_4,e_5,e_6\right)}^{\text{T}}=P-P_d$ ，对误差矢量求导，得到如下的子系统：

A： $\{\begin{array}{l}{\stackrel{\dot{}}{e}}_1=e_2\hfill \\ {\stackrel{\dot{}}{e}}_2=f_{1d}-f_1\hfill \end{array}$

B： $\{\begin{array}{l}\begin{array}{l}{\stackrel{\dot{}}{e}}_3=e_4\hfill \\ {\stackrel{\dot{}}{e}}_4=f_1{e}_5+e_5\left(f_1-f_{1d}\right)\hfill \end{array}\hfill \\ \begin{array}{l}{\stackrel{\dot{}}{e}}_5=e_6\hfill \\ {\stackrel{\dot{}}{e}}_6=f_2-f_{2d}\hfill \end{array}\hfill \end{array}$

由上式，飞行器的轨迹跟踪可转化为下述问题：在初始跟踪误差 $e\left(0\right)$ 条件下，寻找合适的时变状态反馈控制器， $f_1=f_1\left(t,y\right)$ ， $f_2=f_2\left(t,y\right)$ ，使VTOL可以渐近收敛于参考轨迹。由于系统A为线性子系统，设计如下的控制律：

$f_1=f_{1d}+{\lambda }_1\left(e_2+{\lambda }_2{e}_1\right)+{\lambda }_2{e}_2$ ④

${\lambda }_1,{\lambda }_2$ 为正的常数增益且有 ${\lambda }_1>{\lambda }_2$ 。这时子系统A的特征根均为负数，故 $e_1\to 0$ ， $e_2\to 0$ ，( $t\to \infty$ ).但如果子系统B稳定渐进于原点之前，若 $f_1=0$ ，则系统B中的 $f_2$ 便会出现奇异，因此 $e_1,e_2$ 的选取应保证 $f_1$ 非零。根据B系统的具体形式，下面采用反演法设计 $f_2$ 的渐近稳定控制器。第一步，利用中间虚拟量，定义4个误差变量：

$\{\begin{array}{l}\begin{array}{l}{z}_1=e_3\hfill \\ z_2=e_4-{\mu }_1\left(e_3\right)\hfill \end{array}\hfill \\ \begin{array}{l}{z}_3=e_5-{\mu }_2\left(e_3,e_4\right)\hfill \\ z_4=e_6-{\mu }_3\left(e_3,e_4,e_5\right)\hfill \end{array}\hfill \end{array}$ ⑤

上式中， ${\mu }_1,{\mu }_2,{\mu }_3$ 为虚拟量，为使每一状态具有渐近稳定性，下面控制律设计的每一步都会定义一个Lyyapnovo函数，⑤式本质为微分同胚变换，故可通过镇定原系统的状态变量与虚拟反馈间的误差而达到镇定原系统B的目的，具体步骤如下：

1) 求 ${\stackrel{\dot{}}{z}}_1$ ， ${\stackrel{\dot{}}{z}}_1=e_4=e_4+{\lambda }_3{e}_3-{\lambda }_3{z}_1$ ， ${\lambda }_3$ 为正常数增益，令 ${\mu }_1=-{\lambda }_3{e}_3$ ， $V_1=\frac{1}{2}{z}_1^2$ ，则有：

$\{\begin{array}{l}\begin{array}{l}{\stackrel{\dot{}}{z}}_1=-{\lambda }_3{z}_1+z_2\hfill \\ {\stackrel{\dot{}}{z}}_2=f_1{e}_5+\left(f_1-f_{1d}\right)p_{5d}-{\stackrel{\dot{}}{\mu }}_1\hfill \end{array}\hfill \\ {\stackrel{\dot{}}{V}}_1=-{\lambda }_3{z}_1^2+z_1{z}_2\hfill \end{array}$

由上式可知，若 $z_2=0$ ， ${\stackrel{\dot{}}{z}}_1=-{\lambda }_3{z}_1$ ，指数稳定，但 $z_2$ 一般不恒为0，这时引入虚拟控制 ${\mu }_2$ ，使误差 $z_2$ 具备期望的渐近性，为此转入第二步设计：

2) 令 $V_2=V_1+\frac{1}{2}{z}_2^2$ ， ${\mu }_2=\left({\stackrel{\dot{}}{\mu }}_1-z_1-{\lambda }_4{z}_2-p_{5d}\left(f_1-f_{1d}\right)\right)/f_1$ ， ${\lambda }_4$ 为正增益常数。则有：

$\{\begin{array}{l}\begin{array}{l}{\stackrel{\dot{}}{z}}_1=-{\lambda }_3{z}_1+z_2\hfill \\ {\stackrel{\dot{}}{z}}_2=-z_1-{\lambda }_4{z}_2+f_1{z}_3\hfill \end{array}\hfill \\ \begin{array}{l}{\stackrel{\dot{}}{z}}_3=e_6-{\stackrel{\dot{}}{\mu }}_2\hfill \\ {\stackrel{\dot{}}{V}}_2=-{\lambda }_3{z}_1^2-{\lambda }_4{z}_2^2+f_1{z}_2{z}_3\hfill \end{array}\hfill \end{array}$

若 $z_3$ 为0，则 $z_1,z_2$ 在0处指数渐近稳定，但 $z_3$ 一般不恒为0，为使 $z_3$ 具有期望的渐近状态，引入虚拟控制 ${\mu }_3$ ，转入第三步设计：

3) 定义 $V_3=V_2+\frac{1}{2}{z}_3^2$ ， ${\mu }_3=-f_1{z}_2-{\lambda }_5{z}_3+{\stackrel{\dot{}}{\mu }}_2$ ， ${\lambda }_5$ 为正增益，可得：

$\{\begin{array}{l}{\stackrel{\dot{}}{z}}_1=-{\lambda }_3{z}_1+z_2\\ {\stackrel{\dot{}}{z}}_2=-z_1-{\lambda }_4{z}_2+f_1{z}_3\\ {\stackrel{\dot{}}{z}}_3=-f_1{z}_2-{\lambda }_5{z}_3+z_4\\ {\stackrel{\dot{}}{z}}_4=f_2-f_{2}d-{\stackrel{\dot{}}{\mu }}_3\\ {\stackrel{\dot{}}{V}}_3=-{\lambda }_3{z}_1^2-{\lambda }_4{z}_2^2-{\lambda }_5{z}_3^2+z_3{z}_4\end{array}$

同上， $z_4$ 为0时， $z_1,z_2,z_3$ 在0处渐近稳定，但 $z_4$ 一般不恒为0，为使 $z_4$ 具有期望的渐近状态，可以通过 $f_2$ 的选取实现，为此转入最后一步设计：

4) 定义 $V_4=V_3+\frac{1}{2}{z}_4^2$ ，令 $f_2={\stackrel{\dot{}}{\mu }}_3+f_{2}d-{\lambda }_6{z}_4-z_3$ ， ${\lambda }_6$ 为正增益，则有：

$\{\begin{array}{l}{\stackrel{\dot{}}{z}}_1=z_2-{\lambda }_3{z}_1\\ {\stackrel{\dot{}}{z}}_2=f_1{z}_3-z_1-{\lambda }_4{z}_2\\ {\stackrel{\dot{}}{z}}_3=z_4-f_1{z}_2-{\lambda }_5{z}_3\\ {\stackrel{\dot{}}{z}}_4=-z_3-{\lambda }_6{z}_4\\ {\stackrel{\dot{}}{V}}_4=-\left({\lambda }_3{z}_1^2+{\lambda }_4{z}_2^2+{\lambda }_5{z}_3^2+{\lambda }_6{z}_4^2\right)\end{array}$ ⑥

由上式可以看出， $z_1,z_2,z_3,z_4$ 在0处均指数渐近稳定，且虚拟控制量 ${\mu }_1,{\mu }_2,{\mu }_3$ 也渐近稳定趋于0，这样，系统B也是指数渐近稳定。

5. 系统的稳定性分析

在 $f_2$ 的作用下，B系统在原点处渐近稳定。

证明：由推导过程可知， $V_4=\frac{1}{2}\left(z_1^2+z_2^2+z_3^2+z_4^2\right)$ ，

故

$\begin{array}{c}{\stackrel{\dot{}}{V}}_4=z_1{\stackrel{\dot{}}{z}}_1+z_2{\stackrel{\dot{}}{z}}_2+z_3{\stackrel{\dot{}}{z}}_3+z_4{\stackrel{\dot{}}{z}}_4\\ =z_1\left(-{\lambda }_3{z}_1+z_2\right)+z_2\left(f_1{z}_3-z_1-{\lambda }_4{z}_2\right)+z_3\left(z_4-f_1{z}_2-{\lambda }_5{z}_3\right)+z_4\left(-z_3-{\lambda }_6{z}_4\right)\\ =-\left({\lambda }_3{z}_1^2+{\lambda }_4{z}_2^2+{\lambda }_5{z}_3^2+{\lambda }_6{z}_4^2\right)\\ \le -\lambda {\Vert Z\Vert }^2\end{array}$

$\lambda =\min \left({\lambda }_3,{\lambda }_4,{\lambda }_5,{\lambda }_6\right)$

由李雅谱诺夫指数稳定定理，可知：

${\Vert Z\left(t\right)\Vert }^2\le {\text{e}}^{-2\lambda t}{\Vert Z\left(0\right)\Vert }^2$

即

$\Vert Z\left(t\right)\Vert \le \epsilon {\text{e}}^{-\lambda t},\lambda =\Vert Z\left(0\right)\Vert$ ⑦

由⑦可知， $\left|z_i\left(t\right)\right|\le \epsilon {\text{e}}^{-\lambda t}\left(i=1,2,3,4\right)$ ，故 $z_1,z_2,z_3,z_4$ 都指数渐近收敛于原点，可以推出 $e_3\to 0$ ， $e_4\to {\mu }_1$ ， $e_5\to {\mu }_2$ ， $e_6\to {\mu }_3$ ( $t\to \infty$ )。若要 $e_4,e_5,e_6$ 都趋于0，只需 ${\mu }_1,{\mu }_2,{\mu }_3$ 收敛于0即可。 ${\mu }_1=-{\lambda }_3{e}_3$ ，故 ${\mu }_1\to 0$ ， ${\mu }_2=\left({\mu }_1-z_1-{\lambda }_4{z}_2-p_{5d}\left(f_1-f_{1d}\right)\right)/f_1$ ，由 $z_1\to 0$ ， $z_2\to 0$ ，及④中 $f_1$ 的定义，可知 ${\mu }_2\to 0$ 且指数收敛于原点，其导数 ${\stackrel{\dot{}}{\mu }}_2$ 也应指数收敛于原点。由 ${\mu }_3$ 的定义可知， ${\mu }_3$ 也指数渐近收敛于原点。这样就可以说明 $e_4,e_5,e_6$ 都指数趋于0，故系统B渐近稳定于原点。综合以上结果，在控制律 $f_1=f_{1d}+{\lambda }_1\left(e_2+{\lambda }_2{e}_1\right)+{\lambda }_2{e}_2$ 和 $f_2={\stackrel{\dot{}}{\mu }}_3+f_{2}d-{\lambda }_6{z}_4-z_3$ 以及虚拟控制 ${\mu }_1,{\mu }_2,{\mu }_3$ 的作用下，系统A，B是指数渐近稳定的。

6. 仿真结果和讨论

本文利用Matlab软件进行数值仿真，验证所设计的控制器的性能。本文中，取 $\rho =1$ ， ${\lambda }_1=2$ ， ${\lambda }_2=2$ ， ${\lambda }_3=3$ ， ${\lambda }_4={\lambda }_5={\lambda }_6=5.2$ ， $g=9.8\left(\text{m}\cdot {\text{s}}^{-2}\right)$ ，设控制输入 $p_{1d}=10+\sin t$ ， $p_{2d}=0$ 对应的参考轨迹为 ${\stackrel{\dot{}}{x}}_d=1$ ， ${\stackrel{\dot{}}{y}}_d=\cos t$ ， ${\stackrel{\dot{}}{\alpha }}_d=0$ ， $x_d=t$ ， $y_d=10-\sin t$ ， ${\alpha }_d=0$ ，数值仿真结果如下图2和图3所示：

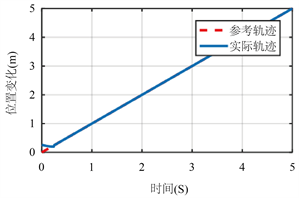
Figure 2. Position x changes with time curve

图2. 位置x随时间变化曲线

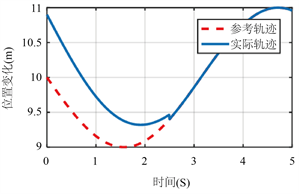
Figure 3. Position y changes with time curve

图3. 位置y随时间变化曲线

从图2和图3可以看出，控制量响应速度较快、在t = 3 s时稳定收敛。相比于文献 [5] 文献 [7] 中的控制方法，本控制器设计方法简单，编程易于实现，可实现垂直起降飞行器的跟踪控制，仿真结果还可以说明，该算法可实现对横向和垂向运动的解耦，实现垂直起降飞行器的快速稳态跟踪。

7. 结语

本文针对欠驱动空间垂直升降器的跟踪控制问题，提出了一种控制器的反演设计方法，首先对这种机械系统的动力学方程进行解耦，解耦后的动力学模型分为两个子系统，然后利用反步法设计了系统的控制器，改设计可以避免一些文献中需要进行黎卡提方程的求解，编程易于实现，适合实际的工程应用。仿真结果也表明，所设计的控制器可以有效地跟踪参考轨迹。