金属接触密封中流体压差对泄漏量的影响研究

Research on the Influence of Fluid Pressure Differential on Leakage in Metal Contact Seals

摘要: 密封是液压系统正常工作的保障，工作在高温高压环境中的液压元件常采用金属接触密封，本文通过有限元仿真从微观角度研究了流–固耦合作用对金属接触密封的泄漏过程的影响。首先基于包含粗糙度均方根与自相关长度的点云函数构建了离散化粗糙面的接触模型，然后提取变形后的接触面进行了单向流–固耦合，分析了流体压力对接触面积和泄漏通道平均高度的影响规律，并计算了在不同压差作用下的泄漏量。研究结果表明：随着压差的增大，流体对金属接触密封接触状态的影响逐渐变大，对流道入口处的形貌影响最大，最后导致密封面的分离度增加。考虑流–固耦合作用后，密封副的泄漏量明显增加，且当流体压差达到接触压力的60%时，会导致泄漏量近似呈指数激增。以上研究成果可以为金属接触密封结构的设计提供指导。

Abstract: Sealing is essential for the normal operation of hydraulic systems, and metal contact seals are commonly used in hydraulic components operating in high temperature and high pressure environments. This paper investigates the influence of fluid-solid coupling on the leakage process of metal contact seals from a microscopic perspective using finite element simulation. Firstly, a contact model of discretized rough surfaces is constructed based on a point cloud function that includes the root mean square roughness and autocorrelation length. Then, the deformed contact surfaces are subjected to one-way fluid-solid coupling, and the influence of fluid pressure on the contact area and average height of the leakage channel is analyzed. The leakage rates under different pressure differentials are also calculated. The research findings show that, as the pressure differential increases, the influence of the fluid on the contact status of the metal contact seal gradually becomes more significant, especially at the inlet of the flow channel, leading to an increase in the degree of separation of the sealing surfaces. Considering the fluid-solid coupling, the leakage rate of the sealing pair significantly increases, and when the fluid pressure differential reaches 60% of the contact pressure, the leakage rate experiences an approximate exponential increase. These research findings could provide guidance for the design of metal contact sealing structures.

1. 引言

在液压系统中，液压控制阀保证了液压系统的稳定。对于应用在高压环境的液压控制阀，金属接触密封是常用的密封形式 [1] 。在金属密封中阀芯与阀座之间相互接触形成密封带并起到密封作用，金属密封的结构相对简单，在相同的使用场景下相比其他密封形式具有良好的耐用性与密封性能 [2] 。但现有的加工技术无法使得工程表面达到完全光滑的标准，将工程表面放大后可以发现其表面布满了大小不一的微凸体 [3] ，两个表面的接触实际上是其表面上微凸体的接触，表面的实际接触面积远小于宏观接触面积。未接触的微凸体周围的空隙相互贯通，形成了泄漏通道，使得流体在压力的作用下由高压侧向低压侧泄漏，金属接触密封的泄漏失效在工程应用中仍有发生 [4] [5] 。

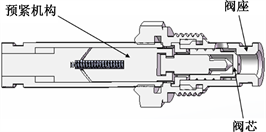
Figure 1. Common metal contact seal structure

图1. 常见的金属接触密封结构

图1为一常见的金属接触密封结构，该系统依靠预紧机构提供接触压力使阀芯与阀座相互接触，并通过这种接触形成密封带。金属接触密封的密封压力通常由电磁铁或者弹簧提供，密封压力过大会导致结构损坏，密封压力过小会导致泄漏量增大，选取合适的密封压力对保证结构的正常运行具有重要意义。过去的一些研究未考虑流体压差对泄漏通道形貌的影响，使用达西公式计算泄漏量，其结论中泄漏量与流体进出口压差呈线性关系 [6] [7] ，在达西公式中流体泄漏量Q公式为 [8] ：

$Q=\frac{KA\text{Δ}p}{\mu l}$ (1)

式中，K为渗透率；A为多孔介质横截面积； $\text{Δ}p$ 为流道压差；μ为流体动力黏度；l密封端面宽度。

但学者们在研究高压环境中工作的金属接触密封结构时发现，随着液体压力的上升，密封结构的泄漏有指数形上升的趋势 [9] ，这与之前的理论不符。

金属密封的泄漏机理是机械密封领域中亟需解决的重要问题，国内外学者已经进行了大量的研究 [10] [11] 。金属表面具有一定的微观形貌，直接计算其泄漏量是十分困难的。目前分析方法主要分为两种，其中一种是通过逾渗理论来揭示金属接触过程中泄漏通道的形貌变化与泄漏特性 [12] [13] 。逾渗理论描述了流体在随机介质中的流动过程，通过孔隙率、迂曲度等参数来反映泄漏通道的形貌特性并计算泄漏量。这种研究方法可以较为准确的反映流体泄漏量的变化，但无法直观反映泄漏通道的形貌变化的过程。另一种则是借助现代计算机仿真技术，构建粗糙表面接触模型，通过数值仿真的方法直接对泄漏通道中流体的流动进行计算 [14] [15] ，进而研究泄漏通道的各种特性。但由于粗糙表面相互接触后形成的泄漏通道具有及其复杂的形貌，这种方法对计算机性能的要求极高，需要占用大量的计算资源。

在仿真软件中构建金属接触模型的主要问题在于金属表面具有不规则的几何结构，这将在建模软件中形成一个复杂的表面，对其划分网格并进行仿真计算需要占用大量的运算资源。为了改善这些问题，文本将使用离散化思想对粗糙表面进行建模。使用点云数据构建大量具有指定离散步长的立方体并进行有序组合来构建仿真模型，这种方法能够将包含复杂三维曲面的体转化为规则的体并且充分保留其三维面的几何结构 [16] 。

本文将从建立有效的粗糙面微观几何形貌入手，逐步构建离散化金属接触密封泄漏模型，通过有限元方法探究流体压差对泄漏过程的影响，从微观角度研究接触泄漏问题，为接触式金属密封结构泄漏的探究提供新的思路和方法。

2. 粗糙表面的构造

为了研究不同条件下金属接触密封泄漏通道的形貌与泄漏量的变化趋势，构建可信的粗糙表面是研究问题的基础。由于大部分工程表面都满足高斯分布的条件 [17] ，本文所构建的随机粗糙表面也采用高斯分布模型。

重构维数为 $M\times N$ 的粗糙表面轮廓，可以用 $\left(M+m\right)\times \left(N+n\right)$ 的符合正态分布的随机序列 $\eta$ 和一个维数为 $m\times n$ 的自相关矩阵α通过线性变换获得，其中随机序列 $\eta$ 满足以下关系：

$E\left({\eta }_{k,l},{\eta }_{a,b}\right)=\{\begin{array}{l}1\text{if}k=a,l=b\hfill \\ 0\text{ifotherwise}\hfill \end{array}$ (2)

式中E是数学期望值。

由于指数型自相关函数表征的粗糙面最贴合实际工程表面的特征 [17] 。所以假设接触密封结构中，金属密封结构表面上微观几何形貌的自相关函数为：

$R\left(x,y\right)={\sigma }^2\exp \left\{-2.3{\left|{\left(\frac{x}{{\tau }_x}\right)}^2+{\left(\frac{y}{{\tau }_y}\right)}^2\right|}^{\frac{1}{2}}\right\}$ (3)

式中𝜎为表面粗糙度的均方根(μm)；exp为自然指数函数； ${\tau }_x$ 为x方向上的自相关长度，即x沿着x方向衰减为初始值的10%时的长度(μm)； ${\tau }_y$ 为y方向上的自相关长度，即y沿着y方向衰减为初始值的10%时的长度(μm)。

本文研究中使用的是各项同性的粗糙表面，即自相关长度 $\tau$ 满足：

$\tau ={\tau }_x={\tau }_y$ (4)

三维表面的自相关函数的定义如下：

$R\left(a,b\right)=E\left\{z\left(k,l\right)z\left(k+a,l+b\right)\right\}$ (5)

式中a与b分别是x与y方向上的自相关长度。

离散形式下，平稳随机过程 $z\left(k,l\right)$ 的自相关函数的定义为：

$R\left(a,b\right)=\frac{1}{\left(M-k\right)\left(N-l\right)}{\displaystyle {\sum }_{a=1}^{M-k}{\displaystyle {\sum }_{b=1}^{N-l}Z\left(k,l\right)Z\left(k+a,l+b\right)}}$ (6)

离散状态下的遍历性粗糙面的自相关函数可以表示为：

(7)

通过自相关函数的定义得到自相关系数矩阵为：

$\begin{array}{l}{R}_{p,q}={\displaystyle {\sum }_{a=1}^{m-p}{\displaystyle {\sum }_{b=1}^{n-q}{\alpha }_{a,b}{\alpha }_{a+p,b+q}}}\\ p=0,1,\cdots ,n-1\\ q=0,1,\cdots ,m-1\end{array}$ (8)

根据上述求得的自相关矩阵和随机序列，即可得到粗糙表面的矩阵：

$Z_{k,l}={\displaystyle {\sum }_{a=1}^m{\displaystyle {\sum }_{b=1}^n{\alpha }_{a,b}{\eta }_{k+a,l+b}}}$ (9)

粗糙度均方根与自相关长度可以分布反映粗糙面高度参数与空间分布情况，而且这两个参数相互独立。通过给定粗糙度均方根与自相关长度数值可以得到具有特定表面形貌的粗糙面，本文中所使用的是粗糙面是在粗糙度均方根 $\sigma =0.4\text{μm}$ ，自相关长度 $\tau =30\text{μm}$ 的条件下建立的。

3. 离散化仿真模型的构建

通过计算机仿真来研究金属微观接触问题时，需要使用算法对获得的点云数据进行曲面拟合来进行曲面建模。随着点云数据的增加，曲面的复杂程度也越来越高，因此在这个过程中还需要对生成的曲面进行平滑与细化处理，才能得到可以进行计算的接触模型。这种方法需要使用大量的运算资源，还会导致处理后的模型失去点云数据中的部分特征 [18] 。

为了改善上述问题，本文将结合离散化建模思想，建立可以完整保留点云信息的离散化接触模型。

3.1. 离散化粗糙面的构建

本节将根据点云信息建立大量具有一定离散步长的立方体，按照点云的排列顺序将这些立方体有序组合并最终获得离散化的粗糙面。点云文件中包含大量的点来描述几何结构，离散化建模需要建立大量的规则立方体，需要借助编程语言来进行快速建模。PythonOCC是一个基于Python编程语言的开源计算机辅助设计与计算机辅助制造工具包，可以用于三维几何数据的建模、分析和可视化操作。本文使用PythonOCC工具包对粗糙面进行参数化建模，具体建模流程如图2所示。

其中立方体的长宽大小等于点云的采样间隔即选取的离散步长；各立方体的高度等于点云中各点的z坐标值加上给定的粗糙面厚度H；各立方体底面中心的x坐标与y坐标为点云中各点的x坐标与y坐标；各立方体底面的z坐标为0。便得到了所需要的名义厚度为H的粗糙面。最终建立的离散化粗糙面如图3所示。

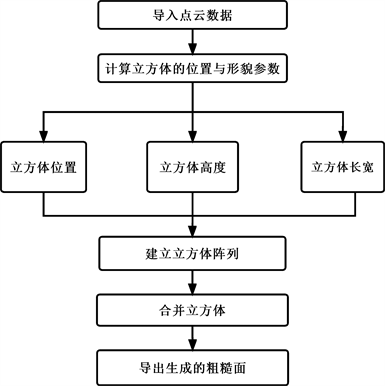
Figure 2. Flowchart of the rough plane constructed in PythonOCC

图2. 在PythonOCC中构建的粗糙平面的流程图

Figure 3. Rough surface discretization model

图3. 粗糙面离散化模型

从图3中可以看出，离散化建模降低了曲面的几何复杂程度，这样生成的模型不仅保留了点云数据中的所有信息，还通过使用离散化元素，提高了模型在仿真软件中处理和分析的速度与兼容性。

3.2. 接触模型的构建

考虑整个金属接触密封结构的微观形貌，对其整体进行仿真分析及其困难。为了简化计算量，取其中长宽为100 μm × 100 μm的高斯型粗糙面建模，建模厚度取10 μm。模型由具有理想光滑平面的体和具有指定表面粗糙度与自相关长度的粗糙面的体两个部分构成，不考虑重力对接触过程产生的影响。之前有研究对比了两组微观接触模型，其中一组将两个具有不同微观形貌的粗糙表面的体进行接触，而另一组将其中一个粗糙面简化为具有理想的光滑平面的体，对比发现两组模型的仿真结果几乎没有差别 [19] 。所以本文也采用粗糙面与理想光滑平面的接触来研究金属接触密封，建立的接触模型如图4所示。

Figure 4. Constructed contact model

图4. 构建的接触模型

使用Ansys Workbench仿真软件对金属接触模型进行研究分析。将金属密封模型中带有微观高斯形貌特征粗糙面的体的下表面固定，对具有理想光滑平面的体的上表面施加作用在Z方向，且向下的压力。设置粗糙面与光滑平面为无摩擦接触。对具有理想平面的体与粗糙面的体的侧面添加无摩擦支撑来保证无滑移、无摩擦的边界条件，具有理想平面的体选用结构钢，为考虑粗糙面的弹塑性变形，其材料选择一般非线性材料中的铝合金，材料属性见表1。

Table 1. Material property table

表1. 材料属性表

3.3. 离散步长对接触模型的影响

在本模型中，离散步长等于单个立方体底面的长宽尺寸，离散步长的选取会直接影响模型的精度。图5为在100 MPa接触压力作用下离散步长为2 μm × 2 μm、粗糙度均方根为0.4 μm、自相关长度为30 μm粗糙面的等效应力与总变形，可以看出在接触应力作用下中两表面并没有完全接触。

离散化建模中，较小的离散步长可以更加准确地捕捉曲面的细节与曲率的变化，而较大的离散步长可以降低模型的复杂程度，本节将使用从同一曲面上获得的点云文件，建立不同离散步长的粗糙面，对比这些粗糙面在接触过程中的仿真精度变化。

本节从大小为100 μm × 100 μm的粗糙表面上分别建立离散步长为10 μm×10 μm、4 μm × 4 μm、2 μm × 2 μm、1 μm × 1 μm的离散化曲面，下图6为各离散步长模型与使用曲线拟合的粗糙面在压力作用下光滑面与粗糙面的接触面积的变化趋势。

如图6所示，当离散步长较大时模型中含有的有效数据较少，其接触面积曲线与其他模型相差较大。随着网格尺寸的减小，各模型的接触面积曲线相互接近，其中离散步长为4 μm × 4 μm、2 μm × 2 μm、1 μm × 1 μm的离散化模型在不同接触压力下相差不超过5%。这些离散化模型相比使用曲线拟合生成粗糙面的模型的接触面积曲线的偏差不超过8%，这些偏差主要来自于拟合过程中带来的偏差。综上所述，随着离散步长的减小，模型的接触曲线将趋于接近并具有良好的精度，过小的网格也会增加所需的计算资源，本文构建的接触模型使用的离散步长为2 μm × 2 μm。

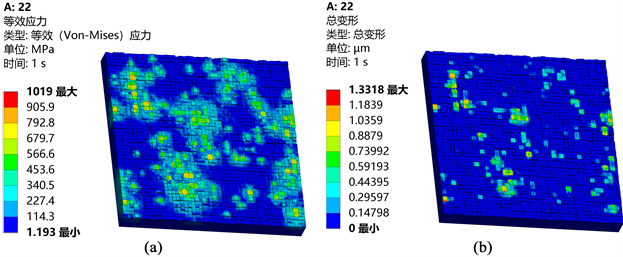
Figure 5. Deformation of rough surface at contact pressure of 100 MPa. (a) Equivalent force on a rough surface at a contact pressure of 100 MPa; (b) Total deformation of rough surface at contact pressure of 100 MPa

图5. 接触压力为100 MPa时粗糙面的变形情况。(a) 接触压力为100 MPa时粗糙面的等效应力；(b) 接触压力为100 MPa时粗糙面的总变形

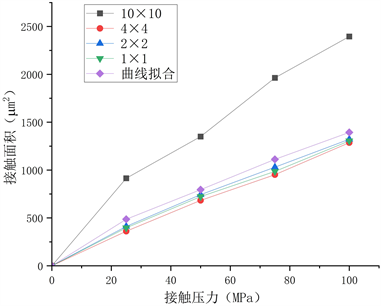
Figure 6. Contact pressure and contact area curves for each model

图6. 各模型的接触压力与接触面积曲线

3.4. 金属接触密封泄漏模型

在金属接触密封发生泄漏时，流体在阀芯阀座两端的压差的推动下流过接触后形成的流道并产生泄漏。在接触过程中仿真流体对接触面的影响是一个复杂的问题，其中的主要问题是在表面相互接近的过程中流体网格的上下边界会发生接触，这将导致流体域的几何拓扑结构发生改变，最终导致仿真分析的无法运行。

本文采用仿真方法如下：在仅受接触压力作用下的接触模型中，创建变形后的未接触部分为流体通道，并对模型整体进行单向的流–固耦合分析，在流体压力、接触压力的作用下模型将达到新的平衡。提取受流体作用变形后模型，通过其的间隙创建泄漏流道，以此流道分析各因素对流道泄漏量的影响，分析在流体压差下泄漏量的变化情况，并得到考虑了单向流–固耦合作用的泄漏模型。

Figure 7. Leakage channel model

图7. 泄漏通道模型

以大小为100 μm × 100 μm的接触模型在100 MPa平均接触应力作用下得到的微流道为例，建立的泄漏通道仿真模型。建立的仿真模型如图7所示，图中灰色部分是泄漏通道，白色部分是密封面的接触部分。该模型忽略了体积力对流体流速的影响。设置模型的左右两面分别为流道压力的出入口，入口压力设置为P，出口压力为大气压强，前后两平面设置为对称边界，其他边界视为壁面。

4. 流体压差对金属接触密封的影响

金属接触密封被广泛的运用于各种液压系统中，随着流体压差的增加，流–固耦合作用对泄漏通道的影响也同样不容忽视。本节将研究流体压差对金属接触密封泄漏的影响。用于接触密封的上下表面在接触压力的作用下相互接近，其接触状态也随之改变，本节使用两表面的接触面积与流道的平均高度来表征泄漏通道形貌的变化，以更好的分析流体压差对金属接触泄漏的影响。本节所用的模型的大小均为100 μm × 100 μm。

4.1. 流体压差对流道形貌的影响

液体在流道中的流动将产生压降，导致流体对接触面作用力的大小不均匀，图8为100 MPa接触压力作用下，流体压差为50MPa时流体的速度分布图，流体在流道的流动过程中，当流道的宽度增加，流体的速度减小，当流道的宽度减小时，流体的速度增大。

下图9为考虑不同流体压差与不考虑流体作用的流道形貌对比，其流道出入口的方向与图7相同。由图9可得，随着流体压差的增大，流道形貌已经很大的变化。流道形貌图中白色的区域为两面的接触区域，灰色区域为提取到的流道。当不考虑流体作用时，接触区域的分布较为平均，接触区域的接触面积较大，流道较窄。随着流体压差的增加，流体作用的增强，两平面逐渐分离，由于流道入口的压力显著高于流道出口的压力，接触区域在出口方向的分布显著多于入口方向。

图10为模型在100 MPa接触压力作用下的接触状况随流体压差的变化曲线。从图中可以看出随着流体压差的增大，流体压力使得接触面达到新的平衡状态，密封面的接触面积变小，泄漏通道的平均高度增大。随着流体压差的上升，模型的接触面积的下降速度与流道平均高度的增加速度都有所提高，这是因为随着流体压差的上升，密封副上发生接触的点更少，这将导致接触面的刚度变小，抵抗变形的能力变弱，继续变形所需的力更小。

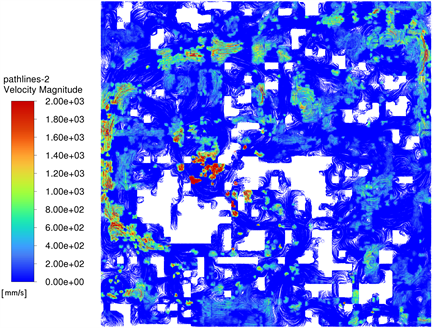
Figure 8. Velocity distribution in the flow channel for a fluid pressure difference of 50 MPa

图8. 流体压差为50 MPa时流道的速度分布图

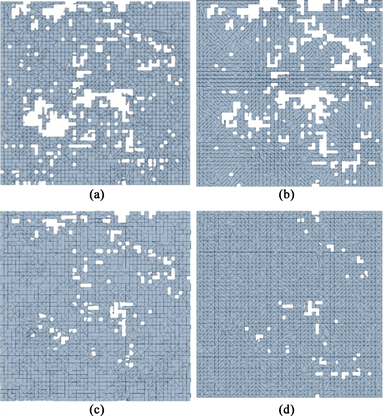
Figure 9. Comparison of flow channel morphology under fluid-solid coupling effect. (a) Disregarding fluid differential pressure; (b) Fluid differential pressure P = 30 MPa; (c) Fluid differential pressure P = 50 MPa; (d) Fluid differential pressure P = 100 MPa

图9. 流–固耦合作用下流道形貌对比图。(a) 不考虑流体作用；(b) 流体压差P = 10 MPa；(c) 流体压差P = 50 MPa；(d) 流体压差P = 100 MPa

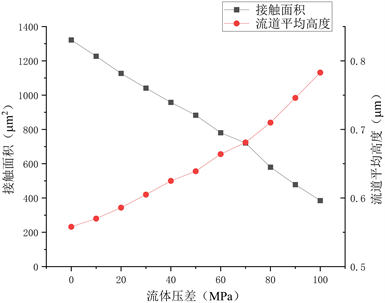
Figure 10. Effect of fluid pressure difference on contact state

图10. 流体压差对接触状态的影响

4.2. 流体压差对泄漏量的影响

金属接触密封具有结构简单可靠的特点，被广泛的使用在高压的工作环境中。在低压条件下，流过密封副两端的流体不会对流道形貌产生显著影响，而高压流体将对密封副产生较大的作用力，使得上下表面的接触状态发生变化，本节将使用所建立的模型研究流体压差对金属接触密封泄漏量的影响。

本文构建的流–固耦合模型在进行泄漏分析时同时考虑了流体压力与接触压力的作用，泄漏量通过泄漏通道出口处的流速积分获得。

Figure 11. Comparison of leakage curves for several models

图11. 几种模型的泄漏量曲线对比图

图11对比了本文建立的流–固耦合模型、不考虑流体作用的仿真模型与根据达西公式计算的泄漏量曲线。其中在根据达西定律来计算泄漏量的模型中，在不考虑流体作用的仿真模型中，孔隙率通过变形后的仿真模型的体积计算获得。进行泄漏分析的流道从仅受接触压力作用后变形的模型中创建得到。达西公式中使用的各项参数也通过不考虑流体作用的仿真模型中创建得到。

由图可得，在根据达西公式计算的数学模型和不考虑流体作用的仿真模型中，泄漏量与液体压差均具有线性关系，且泄漏量数值较为接近，但根据达西公式计算的泄漏量大于不考虑流体作用的仿真模型，这是由于在接触过程中密封面上存在部分间隙没有与出入口联通，并非泄漏通道，这导致使用达西公式计算泄漏量时取得的孔隙率K偏大，造成其泄漏量大于不考虑流体作用的仿真模型。在使用本文建立的流–固耦合模型考虑流体作用后，模型的泄漏量明显增加，随着流体压差的增大，流体对两面的接触状态的影响逐渐增大，两平面逐渐分离，流–固耦合模型的泄漏量超过使用达西公式计算的泄漏量。

在本文使用的流–固耦合模型中，流体改变了两面的接触状态，使得模型泄漏量快速增加。将考虑流体作用的泄漏曲线与文献 [9] 中高压下使用金属接触密封的换向阀的泄漏实验数据对比可以发现，两者的增长趋势一致，金属接触密封结构的泄漏量在高压下有指数增长的趋势。在流体压差为40 Mpa时考虑与不考虑流体作用仿真模型的泄漏曲线相差54%，当流体压差为60 MPa时两曲线相差达到了93%，显然随着流体压差的进一步增大，不考虑流体作用的模型已经无法反映泄漏的实际情况。

5. 结论

(1) 本文结合离散化建模思想，构建了离散化的粗糙表面，发现离散步长在4 μm × 4 μm以内获得的粗糙几何体的仿真误差不超过5%。

(2) 通过对比不同压差下的流道形貌变化，发现在高压作用下，流体对流道入口方向接触状态的影响大于流道出口方向。

(3) 通过单向流–固耦合分析了流体压差对金属接触密封的影响，得到了流体压差对接触情况与泄漏量的影响曲线，在对比其他模型后发现高压流体将显著增加模型的泄漏量，在流体压差达到接触压力的60%时，流体将对接触状态产生显著影响，不考虑流体作用将无法反映实际情况。