基于新型趋近律的PMSM-DTC无感控制

PMSM-DTC Non-Inductive Control Based On New Approach Law

摘要: 在永磁同步电机直接转矩控制(PMSM-DTC)系统中，通常需要通过机械传感器获取转速及位置信息。然而，这种传感器的应用不仅增加了电机系统的成本，而且在复杂环境下难以有效运作。为解决上述问题，本研究引入了模型参考自适应算法，用于跟踪电机的转速和位置，从而实现了PMSM-DTC系统的无感控制。同时，本研究结合了滑模控制，并引入了一种新型的趋近律来改进模型参考自适应算法。通过在Matlab/Simulink中建立仿真模型进行验证，结果表明，所提出的基于新型趋近律的PMSM-DTC无感控制方法能够有效地跟踪电机的转速和位置，从而节约了电机系统的成本。

Abstract: In the permanent magnet synchronous motor direct torque control (PMSM-DTC) system, the rotation speed and position information are usually obtained using mechanical sensors, but they occupy the cost of the motor and are difficult to work in complex environments. To address the above problems, this paper introduces a model reference adaptive algorithm is introduced to track the motor speed and position to achieve non-inductive control of the PMSM-DTC system. A new approach law is introduced in combination with sliding mode control to improve the model reference adaptation, and a simulation is built for verification. The results show that the PMSM- DTC non-inductive control based on the new reaching law used in this article can effectively track the motor speed and position, saving the cost of the motor.

1. 引言

在永磁同步电机直接转矩控制(PMSM-DTC)系统中，通常需要机械传感器获得电机转速及转子位置信息。然而，这种传感器不仅增加了系统的复杂性和成本，还可能导致故障和维护问题的出现。无感控制技术通过对电机的数学模型以及电流值、电压值的利用，能够实现对电机转速及转子位置的准确跟踪，从而避免了传感器的使用，实现电机转子的精确位置和速度控制，而无需依赖机械传感器。

在无感控制中，通常会使用一些先进的控制算法，例如滑模观测器 [1] [2] [3] 、模型参考自适应观测器 [4] [5] [6] 、扰动观测器 [7] [8] [9] 、扩张状态观测器 [10] [11] [12] 等，以实现更高的性能和响应速度。目前国内外，对永磁同步电机的无感控制进行了大量研究，梅柏杉，易蒙，冯江波 [13] 等人对传统MRAS系统的数学模型进行改进，使得数学模型仅和交轴电感有关，避免了定子电阻参与，但是简化后的数学模型也使动态性能变差。邓永彦，王建霖，李华伟 [14] 等人通过对外部扰动进行观测，设计了滑模扰动观测器(SMDO)，并对观测值进行反馈补偿，来提高系统的鲁棒性。诸德宏，赵铭钰 [15] 提出一种超螺旋二阶滑模观测器，减小转子位置和转速的估计误差，针对切换速域过渡不平滑的问题，引入差分进化算法，改进加权系数，实现两种算法的平滑过渡，提高系统的动态性能，但是对于控制系统的设计相对复杂，不利于系统的实时响应。

对上述文献研究分析，为了保证PMSM-DTC系统在保持良好动态响应能力的前提下，实现无传感器控制，提出一种改进型模型参考自适应(Improved Model Reference Adaptive System, IMRAS)。首先引入MRAS算法进行转速和位置跟踪，并根据滑模控制的优点，设计了一种的基于新型趋近律的IMRAS观测器用于PMSM-DTC系统。

2. PMSM-DTC系统原理

永磁同步电机是一种多参数、高耦合、非线性的复杂控制系统，对永磁同步电机进行无感控制需要对其进行建立精确的数学模型，本文以表贴式永磁同步电机为研究对象，为了简化电机模型，忽略铁芯损耗和涡流损耗，在d-q旋转坐标系下，PMSM电压方程公式如下：

$\{\begin{array}{l}{u}_d=R_s{i}_d+\frac{\text{d}{\psi }_d}{\text{d}t}-{\omega }_r{\psi }_q\\ u_q=R_s{i}_q+\frac{\text{d}{\psi }_q}{\text{d}t}+{\omega }_r{\psi }_d\end{array}$ (1)

在d-q旋转坐标系下，PMSM磁链方程公式如下：

$\{\begin{array}{l}{\psi }_d=L_d{i}_d+{\psi }_f\\ {\psi }_q=L_q{i}_q\end{array}$ (2)

在d-q旋转坐标系下，PMSM转矩方程公式如下：

$T_e=\frac{3}{2}{p}_n{i}_q\left[i_d\left(L_d-L_q\right)+{\psi }_f\right]$ (3)

式中，u_d、u_q——d-q轴定子电压；L_d、L_q——d-q轴电感；i_d、i_q——d-q轴定子电流；R_s——定子电阻；p_n——极对数；ω_r——电机角速度；ψ_f——转子永磁体磁链。且表贴式永磁同步电机L_d = L_q = L_s，所以表贴式PMSM转矩方程可简化为：

$T_e=\frac{3}{2}{p}_n{i}_q{\psi }_f$ (4)

式中，T_e为电磁转矩，ψ_f为定子磁链。

PMSM-DTC系统主要由五个基本模块组成：转速环PI控制器、滞环控制器、开关表、逆变器以及电磁转矩和定子磁链的估算模块。PMSM-DTC系统框图如图1所示，首先，对电机的电压和电流进行实时检测。通过估算模块，根据电压和电流值计算出电磁转矩Te和磁链ψ_s的实际数值。接着，将转速环PI控制器输出的转矩期望值与实际转矩值Te相减，得到误差输出，作为转矩滞环控制器的输入。同时，将实际磁链值ψ_s与磁链期望值相减，得到误差输出，作为磁链滞环控制器的输入。根据转矩滞环控制器和磁链滞环控制器的输出状态以及定子磁链所在的扇区，对逆变器输出脉冲信号进行分析，控制电压源逆变器的导通和关断，以实现电机调速控制系统的快速响应 [16] 。

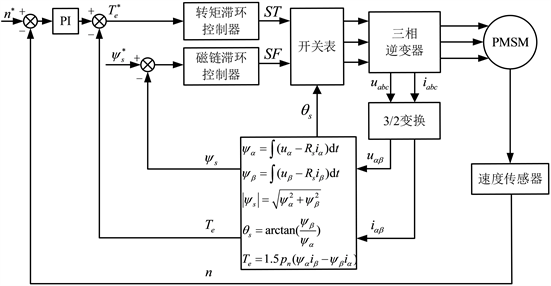
Figure 1. PMSM-DTC system block diagram

图1. PMSM-DTC系统框图

3. MRAS控制原理

不要使用空格、制表符设置段落缩进，不要通过连续的回车符(换行符)调整段间距MRAS由参考模型与可调模型两部分组成，将两个模型的误差信号输入至被控制对象系统之中，并反馈给自适应机构，使得误差收敛至0，达到转速估计的目的，本文采用MRAS并联结构，系统框图如图2所示。

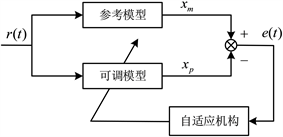
Figure 2. MRAS parallel structure system block diagram

图2. MRAS并联结构系统框图

MRAS的并联结构参考模型公式如下：

${\stackrel{\dot{}}{x}}_m=A_m{x}_m+B_{m}r$ (5)

可调模型公式如下：

${\stackrel{\dot{}}{x}}_p=A_p{x}_p+B_{p}r$ (6)

误差矢量e为A_p与B_p的广义误差矢量，公式如下：

$e=x_m-x_p$ (7)

选取自适应结构的自适应率公式如下：

$\{\begin{array}{l}{A}_p={\displaystyle {\int }_0^t{F}_1\left(v,\tau ,t\right)\text{d}\tau }+F_2\left(v,t\right)+A_{p0}\\ B_p={\displaystyle {\int }_0^t{G}_1\left(v,\tau ,t\right)\text{d}\tau }+G_2\left(v,t\right)+B_{p0}\end{array}$ (8)

以PMSM-DTC为控制对象，结合式(1)、式(2)可得系统参考模型公式如下：

$\{\begin{array}{l}\frac{\text{d}{i}_d}{\text{d}t}=-\frac{R_s}{L_d}{i}_d+\omega i_q\frac{L_q}{L_d}+\frac{u_d}{L_d}\\ \frac{\text{d}{i}_q}{\text{d}t}=-\frac{R_s}{L_q}{i}_q-\omega i_d\frac{L_d}{L_q}-\frac{{\psi }_f}{L_q}\omega +\frac{u_q}{L_q}\end{array}$ (9)

令式(9)中：

${i^{\prime }}_d=i_d+\frac{{\psi }_f}{L_s},{i^{\prime }}_q=i_q,{u^{\prime }}_d=u_d+\frac{R_s{\psi }_f}{L_s},{u^{\prime }}_q=u_q$ (10)

则式(9)可简化公式如下：

$\{\begin{array}{l}\frac{\text{d}}{\text{d}t}{i^{\prime }}_d=-\frac{R_s}{L_s}{i^{\prime }}_d+\omega {i^{\prime }}_q+\frac{1}{L_s}{u^{\prime }}_d\\ \frac{\text{d}}{\text{d}t}{i^{\prime }}_q=-\frac{R_s}{L_s}{i^{\prime }}_q-\omega {i^{\prime }}_d+\frac{1}{L_s}{u^{\prime }}_q\end{array}$ (11)

令式(11)中：

$A=\left[\begin{array}{cc}-\frac{R_s}{L_s}& \omega \\ -\omega & -\frac{R_s}{L_s}\end{array}\right];B=\frac{1}{L_s};i^{\prime }=\left[\begin{array}{c}{i^{\prime }}_d\\ {i^{\prime }}_q\end{array}\right];v^{\prime }=\left[\begin{array}{c}{u^{\prime }}_d\\ {u^{\prime }}_q\end{array}\right]$ (12)

并联可调模型则可以写为：

$\frac{\text{d}}{\text{d}t}{i}^{\prime }=A{i}^{\prime }+B{v}^{\prime }$ (13)

4. 新型趋近律MRAS观测器

滑模指数趋近律公式如下：

$\stackrel{\dot{}}{s}=-\epsilon \mathrm{sgn}\left(s\right)-ks\begin{array}{cc}& \epsilon >0,k>0\end{array}$ (14)

本文对指数趋近律进行改进，在等速项中引入自适应函数，设计一种新型滑模趋近律，公式如下：

$\stackrel{\dot{}}{s}=-a_1\phi \left(s\right)\mathrm{sgn}\left(s\right)-a_{2}s\begin{array}{cc}& a_1>0,a_2>0\end{array}$ (15)

其中自适应连续函数公式如下：

$\phi \left(s\right)=\frac{m}{1+e^{-ns}}\begin{array}{cc}& m>0,n>0\end{array}$ (16)

自适应律可以由Popov积分不等式的逆向求解得到，自适应律公式如下：

${\hat{\omega }}_e={\displaystyle {\int }_0^t{K}_i\left(i_d{{\hat{i}}^{\prime }}_q-{{\hat{i}}^{\prime }}_d{i^{\prime }}_q\right)\text{d}\tau }+K_p\left(i_d{{\hat{i}}^{\prime }}_q-{{\hat{i}}^{\prime }}_d{i^{\prime }}_q\right)$ (17)

对式(17)进行拉普拉斯变换，可得转速公式如下：

${\hat{\omega }}_e=\frac{K_i}{s}\left(i_d{{\hat{i}}^{\prime }}_q-{{\hat{i}}^{\prime }}_d{i}^{\prime }\right)+K_p\left(i_d{{\hat{i}}^{\prime }}_q-{{\hat{i}}^{\prime }}_d{i^{\prime }}_q\right)$ (18)

令式(18)中：

$\sigma =i_d{{\hat{i}}^{\prime }}_q-{{\hat{i}}^{\prime }}_d{i^{\prime }}_q$ (19)

则式(18)可简化公式如下：

${\hat{\omega }}_e=\frac{K_i}{s}\sigma +K_p\sigma$ (20)

对于此非线性方程， ${\hat{\omega }}_e$ 是系统的控制变量。将积分滑模面定义为系统的滑模面，可得滑模面公式如下：

$s=\sigma +{\displaystyle \int k\sigma \text{d}t}\begin{array}{cc}& k>0\end{array}$ (21)

对上式两边同时求导，可得公式如下：

$\stackrel{\dot{}}{s}=\stackrel{\dot{}}{\sigma }+k\sigma \begin{array}{cc}& k>0\end{array}$ (22)

对 $\sigma$ 两边同时求导，可得公式如下：

$\stackrel{\dot{}}{\sigma }={\stackrel{\dot{}}{i}}_d{{\hat{i}}^{\prime }}_q+{\stackrel{\dot{}}{i}}_d{\stackrel{\dot{}}{{\hat{i}}^{\prime }}}_q-{\stackrel{\dot{}}{{\hat{i}}^{\prime }}}_d{i^{\prime }}_q-{{\hat{i}}^{\prime }}_d{\stackrel{\dot{}}{i^{\prime }}}_q$ (23)

将式(11)代入上式，可得公式如下：

$\stackrel{\dot{}}{\sigma }={\stackrel{\dot{}}{i}}_d{\widehat{i^{\prime }}}_q-{\widehat{i^{\prime }}}_d{\stackrel{\dot{}}{i^{\prime }}}_q-\frac{R_s}{L_s}{i}_d{\widehat{i^{\prime }}}_q-\hat{\omega }{\widehat{i^{\prime }}}_d{i}_d+\frac{1}{L_s}{u^{\prime }}_q{i}_d+\frac{R_s}{L_s}{{\hat{i}}^{\prime }}_d{i^{\prime }}_q-\hat{\omega }{{\hat{i}}^{\prime }}_q{i^{\prime }}_q-\frac{1}{L_s}{u^{\prime }}_d{i^{\prime }}_q$ (24)

对式(24)整理化简，可得公式如下：

$\stackrel{\dot{}}{\sigma }={\stackrel{\dot{}}{i}}_d{\widehat{i^{\prime }}}_q-{\widehat{i^{\prime }}}_d{\stackrel{\dot{}}{i^{\prime }}}_q+\frac{R_s}{L_s}{{\hat{i}}^{\prime }}_d{i^{\prime }}_q-\frac{R_s}{L_s}{i}_d{\widehat{i^{\prime }}}_q+\frac{1}{L_s}{u^{\prime }}_q{i}_d-\frac{1}{L_s}{u^{\prime }}_d{i^{\prime }}_q-\hat{\omega }\left({\widehat{i^{\prime }}}_d{i}_d+{{\hat{i}}^{\prime }}_q{i^{\prime }}_q\right)$ (25)

令式(25)中：

$\{\begin{array}{l}{f}_1={\stackrel{\dot{}}{i}}_d{\widehat{i^{\prime }}}_q-{\widehat{i^{\prime }}}_d{\stackrel{\dot{}}{i^{\prime }}}_q+\frac{R_s}{L_s}{{\hat{i}}^{\prime }}_d{i^{\prime }}_q-\frac{R_s}{L_s}{i}_d{\widehat{i^{\prime }}}_q+\frac{1}{L_s}{u^{\prime }}_q{i}_d-\frac{1}{L_s}{u^{\prime }}_d{i^{\prime }}_q\\ f_2={\widehat{i^{\prime }}}_d{i}_d+{{\hat{i}}^{\prime }}_q{i^{\prime }}_q\end{array}$ (26)

则式(25)可简化公式如下：

$\stackrel{\dot{}}{\sigma }=f_1-f_2\hat{\omega }$ (27)

结合式(15)、式(22)和式(27)，可得转速估计公式如下：

$\hat{\omega }=\frac{f_1+a_1\phi \left(s\right)\mathrm{sgn}\left(s\right)+a_{2}s+k\sigma }{f_2}$ (28)

对式(28)等式两边积分，可以得到转子位置估计公式如下：

$\hat{\theta }={\displaystyle \int \hat{\omega }\text{d}\tau }$ (29)

5. 仿真验证

本文在MRAS观测器中引入了基于新型趋近律的滑模控制，取代传统MRAS中的PI环节，设计了一种基于IMRAS算法的观测器来估计转速和转子位置角，基于IMRAS算法的PMSM-DTC系统结构图如图3。为了验证该算法的合理性，在MATLAB/Simulink软件仿真实现PMSM-DTC的无位置传感器控制，仿真如图4。实验采用如下仿真条件：直流母线电压Udc = 310 V，定子电感Ls = 6.5 mH，定子电阻Rs = 1.4Ω，定子磁链ψ_f = 0.13 Wb，极对数pn =3，转动惯量J = 0.003 kg∙m²，给定转速1000 rpm，给定磁链0.3 Wb，在0.2 s时，突加1.5 N∙m的负载，观察系统转速波形，速度误差波形与转子位置波形。

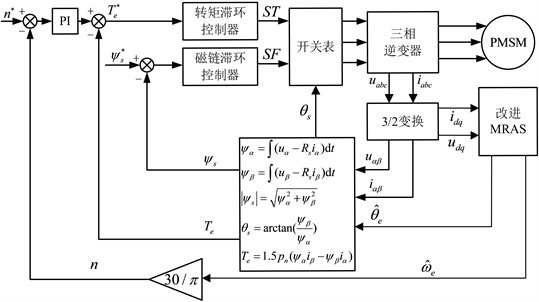
Figure 3. PMSM-DTC system structure diagram based on IMRAS

图3. 基于IMRAS算法的PMSM-DTC系统结构图

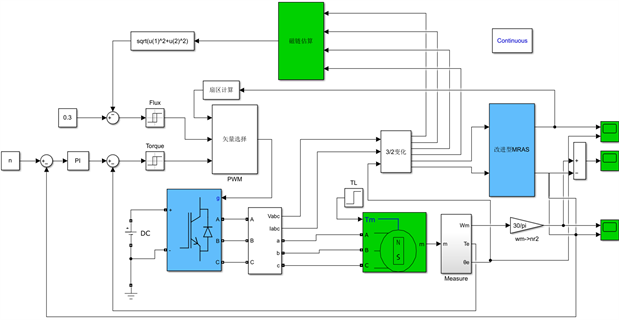
Figure 4. PMSM-DTC system simulation based on IMRAS algorithm

图4. 基于IMRAS算法的PMSM-DTC系统仿真

通过图5、图6可以看出，在启动阶段，电机达到约1200 rpm，估计转速与实际转速误差约为100 rpm，0.03 s后系统达到给定转速1000 rpm，转速误差稳定在40 rpm上下浮动，说明本文所采用的IMRAS算法能够有效的跟踪实际转速，并且保留了PMSM-DTC系统快速响应的优点。当系统给定负载1.5 N∙m时，系统转速有所下降，不过在很短时间内，回复至给定转速1000 rpm，转速误差波形并没有变形，系统估计转速也能很好的跟踪实际转速，说明本文所采用的IMRAS算法在突加负载的情况下也能很好的跟踪转速，实现了PMSM-DTC各阶段转速追踪。通过图7可以看出，估计转子位置与系统实际转子位置近乎重叠，说明本文所采用的IMRAS算法对于转子在各个阶段都有很好的追踪效果。

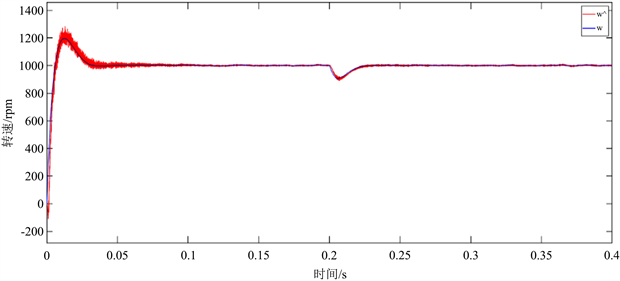
Figure 5. IMRAS variable load speed waveform

图5. IMRAS变载转速波形

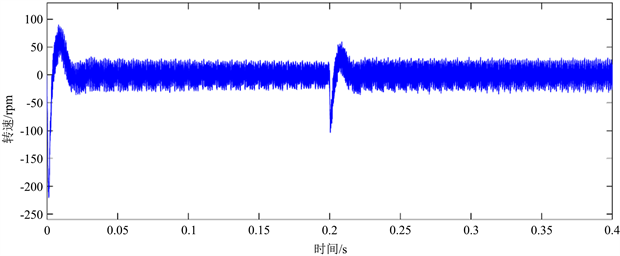
Figure 6. IMRAS variable load speed error

图6. IMRAS变载速度误差

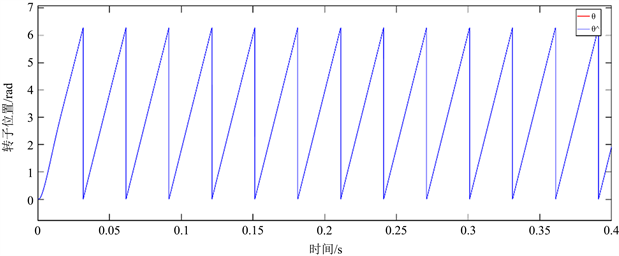
Figure 7. IMRAS variable load rotor position

图7. IMRAS变载转子位置

6. 结束语

本文在PMSM-DTC系统引入了模型参考自适应算法来代替传统DTC系统中的速度位置传感器，并结合滑模控制的优点设计了一种新型趋近律，来对电机转速和转子位置进行跟踪，通过理论推导及仿真分析，在设定高速变载的实验条件下，实验结果表明，本文设计的IMRAS算法有着良好的动态响应能力，转速误差控制在一定范围，转子位置也实现了同步跟踪，证明了本文所设计的IMRAS算法在不影响PMSM-DTC优秀动态响应能力的基础上，实现了对电机转速位置的跟踪，降低了电机成本，同时也具有较好的抗干扰性。