1. 引言
在“工业4.0”、人工智能、物联网技术革命引领下,喷涂机器人的智能化研发已经拉开帷幕,得到了快速发展并进行了一定程度的工业化应用,在喷涂机器人仿真软件方面,产生了机器人运动学、动力学离线仿真技术,扇面模型及膜厚仿真技术,喷涂机器人在线轨迹生成技术 [1] 。潘洋 [2] 等人在平面喷涂模型研究的基础上,采用最小二乘自然二次曲面拟合法对复杂曲面进行拟合,并采用多段分割曲线逼近目标函数的方法分析了相邻两条轨迹间的涂料堆积情况。
近年来,随着机器学习和人工智能技术的不断发展,基于数据驱动的轨迹规划方法逐渐受到关注,通过学习大量的喷涂数据和工件表面特征,能够实现对复杂工件的精准轨迹规划,从而提高了喷涂质量和效率 [3] 。袁子祺 [4] 等人研发了一种智能喷涂机器人小车,采用了高精度喷涂控制系统的喷涂技术,能获得高质量的喷涂效果。在实际工业生产中,为了进一步提高喷涂机器人在喷涂作业过程中的可靠性和稳定性,需要对喷涂运动轨迹进行轨迹规划 [5] [6] 。喷涂机器人轨迹规划的主要目标是确保在工件表面均匀覆盖喷涂材料的同时,最大限度地提高喷涂效率和质量 [7] 。然而,喷涂机器人在实际应用中面临着一个关键挑战,即如何在保证喷涂质量的前提下实现高效的轨迹规划。传统的轨迹规划方法往往依赖于经验性的手动设定或基于简单规则的自动规划,无法充分考虑到工件表面的复杂形状和材料特性,导致喷涂质量无法得到有效控制 [8] 。为此,如何提高喷涂质量的喷涂机器人轨迹规划是当下应该研究和解决的重心。
本文在传统喷涂轨迹规划不考虑喷涂涂层质量以及喷涂轨迹稳定性的基础上,建立涂层模型,分析喷涂间距对喷涂涂层质量均匀性的影响,通过设定好工艺参数,得到最佳喷涂间距。提出一种提高喷涂厚度均匀性的轨迹规划方法,最后通过仿真验证了轨迹的可执行性和可靠性。
2. 喷涂涂层厚度分布模型的建立
喷涂涂层厚度积累的过程与喷枪分布模型有很大关系,为了更好的研究喷涂距离以及机器人喷涂轨迹规划的问题,建立涂层厚度模型具有重要意义,并且能够预测喷涂质量,为后续轨迹规划稳定性和可执行性建立依据 [9] 。
根据喷涂涂料的沉积范围,可以将平面涂层厚度生长模型分为两类,一类是有限范围模型,另一类是无限范围模型 [10] 。有限范围模型包括抛物线分布模型、椭圆双β分布模型等;无限范围分布模型主要包括高斯分布模型和柯西分布模型,喷枪在无穷远处沉积速率可以忽略 [11] 。对于无限范围模型喷涂建立繁琐且喷涂精度不高的问题,本文选用椭圆双β分布模型,如图1所示,喷涂工件区域为椭圆形。
沿着喷涂宽度方向以及涂层厚度方向,服从于β值为β1、β2的双β模型,椭圆双β分布模型表达如下:
(1)
其中a和b分别是椭圆的大直径和小直径;β1和β2分别为X和Y方向的沉积系数;
是喷涂表面上任何点的涂层厚度的函数。
X方向上服从β1分布,Y方向上服从β2分布,可得到Y方向和X方向最大涂层厚度
分别满足:
(2)
(3)
其中:
,
。
对椭圆双β涂层厚度分布模型在MATLAB进行仿真,得到椭圆双β分布模型如图2所示。
3. 喷涂距离对涂层质量的影响
3.1. 涂层厚度建模
上述基于椭圆双β分布模型,分析了在喷涂过程中,喷涂区域内点的涂层厚度满足分布曲线规律。为了达到涂层均匀性的要求,提出一种改进喷枪喷涂距离的方法,通过仿真得到最佳喷涂间距。
在实际喷涂过程中,喷涂区域两边的涂层厚度是比较薄,而中间区域比较厚,如图3是喷涂过程中涂层的累积进程。假设点A的坐标为
。喷枪的垂直投影从o沿轴y的正方向移动,当喷枪椭圆形喷涂区域的一个边界到达A点时,A点的涂层开始累积。喷枪继续移动。当喷枪椭圆形喷涂区域的另一边界离开A点时,A点的涂层停止堆积。
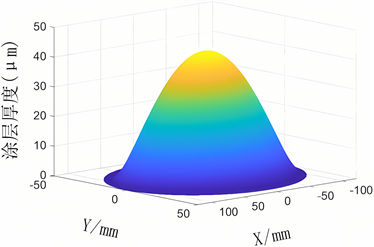
Figure 2. Elliptical two-β distribution model
图2. 椭圆双β分布模型
喷涂速度为匀速v时,那么A点的厚度积累时间为:
(4)
所以A点的涂层厚度为:
 (5)
(5)
式中R为喷涂区域的喷枪半径, g为最大涂层堆积率。当喷枪的匀速v增大时,涂层的累积时间t将减小。
3.2. 涂层距离的测定
在喷涂过程中,需要将两个相邻的喷涂重叠。根据式5工作面任意点的涂层厚度分布规律,两次喷涂之间的喷涂间距确定为l (
)。基于涂层厚度的函数,推导了平面上两次喷涂和重叠零件的涂层厚度的数学表达式:
(6)
设定相关参数:喷枪半径R = 14 cm,最大涂层堆积率g = 0.01,v = 4 cm/s,模拟得到了不同喷枪喷涂间距的涂层厚度效果图,如图4所示。
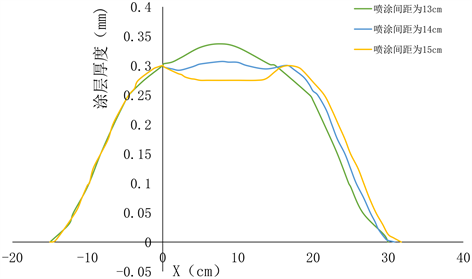
Figure 4. Coating thickness at different pitches
图4. 不同间距下的涂层厚度
从上图得到的对比数据如下表1。

Table 1. Comparison of spraying thickness differences between different spraying spacing
表1. 不同喷涂间距喷涂厚度差异比较
在表1中,喷涂间距从l = 13 cm逐渐增加,涂层厚度差逐渐减小,直到距离l = 14 cm。当间距再次增大时,涂层厚度差逐渐增大。从对比中可以看出,当喷涂间距为整数值且l = 14 cm时,涂层厚度差异最小,最佳喷涂间距为l = 14 cm。
4. 基于涂层厚度均匀性的轨迹规划设计
在机器人喷涂作业的过程中,喷涂机器人的喷涂厚度均匀性会受到机械臂末端移动速度的影响。将待喷涂工件进行区域的划分,通过选择上节分析的最佳喷涂间距,在工件上下两侧为缓冲区,得到如图5的工件喷涂设计图。缓冲区宽度可按照如下公式计算。
(7)
其中D为待喷涂工件宽度,L为整个区域宽度。
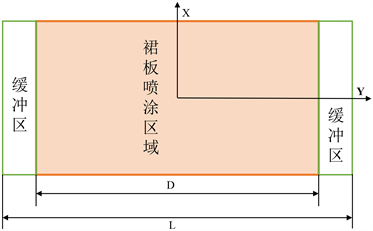
Figure 5. Workpiece spraying design drawing
图5. 工件喷涂设计图
如图6显示了喷枪的整体喷涂轨迹设计图。X轴方向上每次喷涂量为d,d为喷涂重叠长度,最后通过第二小节的椭圆双β模型,计算喷涂量d,S是X轴上某一点的沉积厚度。
传统喷涂工艺是直接在待喷涂的平板上进行的,忽略了喷涂过程中喷枪速度变化造成的Y轴方向喷涂厚度不均匀的问题,因此把缓冲区设置在喷枪变速阶段的喷涂过程,保证工件在Y轴方向上的涂层厚度均匀。
5. 喷涂机器人仿真实验
前面小节,我们对喷涂机器人喷涂间距优化以及喷涂轨迹规划进行了研究,本节基于Robot studio仿真软件,对裙板曲面工件进行喷涂轨迹仿真。
5.1. 碰撞检测
在对喷涂工件进行喷涂的过程中,由于喷涂轨迹规划的不合适以及曲面曲率较大原因,都有一定可能导致喷枪与待喷涂工件发生碰撞,从而使喷枪及工件的破坏,造成严重的损失。所以我们需要在喷涂中,进行碰撞检测如图7所示,检测喷枪与待喷涂工件是否碰撞,采取修改碰撞设置,当发生碰撞时,喷涂工件表面将会变成红色。
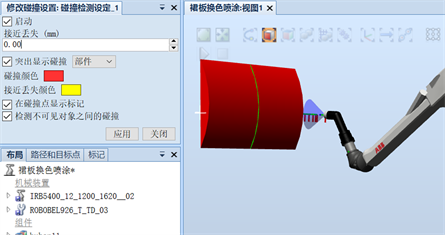
Figure 7. Schematic diagram of collision detection
图7. 碰撞检测示意图
5.2. 机器人喷涂路径仿真
完成碰撞检测模型之后,根据第4小节喷涂轨迹的设计,根据轨迹规划算法生成喷涂轨迹,在生成的轨迹上选择特征节点并且转换为喷枪的位姿。
通过轨迹规划算法生成可连续的喷涂轨迹,如图8所示。
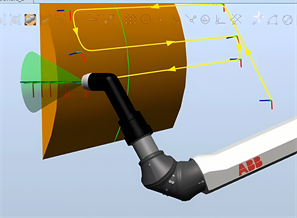
Figure 8. Simulation of robot spraying surface trajectory
图8. 机器人喷涂曲面轨迹仿真
为了保证机器人喷涂曲面裙板运行速度的稳定性和喷涂均匀性,采用圆弧插补算法优化,喷涂优化仿真结果如图9所示。
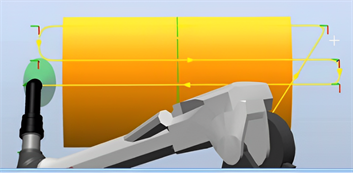
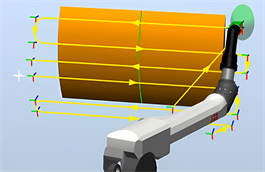
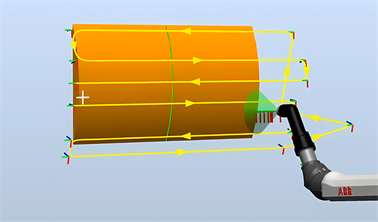
Figure 9. Simulation of arc interpolation optimization of robot spraying path
图9. 机器人喷涂路径圆弧插补优化仿真
5.3. 仿真分析
机器人喷涂路径的实现实际是机器人各关节轴变化产生的结果,根据仿真喷涂运行轨迹实时记录运行轨迹中位姿点的关节轴角度变化进行仿真分析,ABBIRB5500机器人6个关节轴角度变化曲线如下图10所示。
根据机器人6个关节轴的角度变化时间曲线可知,关节轴1开始角度变化较大,运行后面趋于平稳;关节轴2、关节轴3、关节轴4角度变化曲线相似;关节轴5和关节轴6角度变化曲线相似。结合机器人实时关节轴角度变化与轨迹仿真可知,当喷涂路径从一个子区域转到另一个子区域时,各个轴关节的角度变化最明显。但整个喷涂路径中机器人关节轴角度变化都处于机器人IRB5500可允许的角度范围内,并在仿真过程中能平稳执行该段路径轨迹。
6. 结论与展望
本文通过喷涂涂层厚度模型的分析与建立,确定喷枪分布模型为椭圆双 分布模型,并研究了喷涂距离对涂层质量的影响,得出最佳喷涂距离。针对传统轨迹规划方法在喷涂过程中不考虑涂层厚度均匀性的问题,本文提出一种涂层厚度均匀性的轨迹规划方法,设立缓冲区和喷涂区,保证工件在Y轴方向涂层厚度更加均匀。在Robot studio仿真软件建立喷涂仿真平台,根据喷涂机器人工作过程中各关节轴角度变化并对喷涂过程进行碰撞监测,验证了喷涂轨迹的可执行性和合理性,为喷涂机器人在喷涂质量轨迹规划上提供有力的依据和实验仿真基础。