1. 引言
齿轮减速器在工业生产制造中应用广泛,具有传动效率高等特点,箱体是齿轮箱重要的组成部分,其内部结构复杂。箱体在传动过程中受到啮合冲击和外部载荷时,很容易产生振动和变形,这种振动会加剧齿轮的磨损以及产生很大的噪声,一定程度上对齿轮箱的寿命有影响 [1] 。因此,在设计箱体时有必要对其进行有限元分析,从而避免激励频率接近箱体的固有频率,使其发生共振。大量学者对减速器箱体进行了深入的研究,王鑫兴等 [2] 对搅拌车减速器箱体采用变密度法进行拓扑优化以完成轻量化设计,并对优化后的箱体进行仿真分析和试车实验,结果表明箱体整体性能有所提升。张楠等 [3] 在减速器箱体轴承座孔处施加动态激励进行分析得到动刚度频响曲线,并进行拓扑优化改进了危险频率下的箱体结构。刘五合等 [4] 研究了基于声学超材料下的减速器箱体振动噪声问题,分别通过缩比模型和实验共同验证了超材料方案的有效性。王文龙等 [5] 建立齿轮减速器的刚柔耦合动力学模型并分析其共振频率特点,通过齿轮修形改善了其振动噪声问题,并通过仿真和实测验证了方案的合理性。何鹏辉等 [6] 对压裂泵减速器箱体进行仿真分析并结构优化,所设计的箱体的综合应力和变形量均满足使用要求。
本文通过建立单级圆柱齿轮减速器箱体的有限元模型,利用ANSYS Workbench分析软件对减速器箱体的模态和振动特性进行了计算,得到了齿轮箱的前6阶模态以及应力分布云图和变形分布云图。同时在模态分析的基础上,对齿轮箱箱体进行了谐响应分析,得到了齿轮箱体在不同方向,不同位置的位移与频率响应曲线。基于以上分析,箱体的强度在许可范围之内,同时为箱体的可靠性和减振提供理论依据。
2. 减速器箱体静力学分析
2.1. 静力学分析简介
静力学主要是在固定载荷作用的情况下去分析其结构的变化,系统的惯性、阻尼和与时间相关的量等因素对系统的影响可以不考虑 [7] ,其公式为:
(1)
该公式中,
为系统刚度矩阵,
是位移矢量,
则是力矢量。
2.2. 静力学分析前的准备工作
在进行有限元分析之前,首先建立减速器箱体的三维模型,单级圆柱齿轮减速器箱体采用上下箱体结构,分为箱盖、箱座两个部分。为了方便操作,通过布尔计算将上下箱体结构变为一个整体,其圆角、倒角等结构因为会影响到受力情况得以保留。如图1所示,是使用三维软件建立的减速器箱体三维结构简化模型,将三维模型保存为stp文件并导入ANSYS软件。
根据实际情况,减速器箱体材料为灰铸铁,其材料具体属性如表1所示。

Table 1. Material properties of reducer box
表1. 减速器箱体的材料属性
减速器箱体分为箱底和箱盖两个部分,这两部分的接触定义为绑定接触。使用workbench划分网格,使用的是四面体单元,网格划分模式采用自由网格划分方法,设置Relevance为40,采用Curvature网格细化方法。设置好上述参数,经过网格划分,共得到100,749个单元 [8] ,其网格划分如图2所示。

Figure 2. Mesh division of the reducer box
图2. 减速器箱体的网格划分
首先进行载荷分析,齿轮啮合产生的载荷作用在轴承上,然后传递到箱体轴承座上。箱体轴承座部分所受载荷可以分解为径向和轴向载荷,其中径向载荷可以等效为120˚范围内余弦均布压力 [9] ,通过Workbench的Bearing Load来施加。对于轴向载荷,则可以等效为作用于底座的力和力矩的形式 [10] 。根据工作实况,对减速器箱体的底座的四个螺栓面施加固定约束,如图3所示为对减速器箱体静力学分析前的准备工作。
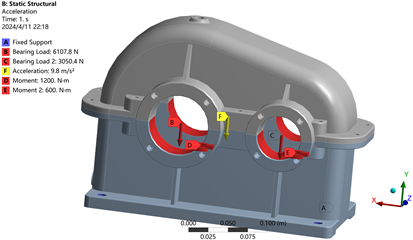
Figure 3. Adding Fixed Support to the bottom of the box and applying loads
图3. 对箱底添加Fixed Support固定约束和施加载荷
2.3. 静力学仿真结果分析
经过ANSYS Workbench软件分析计算所得到的总位移云图及X、Y、Z方向上的云图和等效应力、应变图如图4所示。
对于材料HT250,
是许用安全系数 [11] ,取
,故许用应力:
(2)
由上图可以看出,齿轮箱X方向上位移最大点在输出轴轴承孔位置,最大位移为0.01167 mm;齿轮箱Y方向上位移最大点在齿轮箱底部的两侧,最大位移为0.00041 mm;齿轮箱Z方向上位移最大点在输出轴的左侧部位,最大位移为0.01175 mm。减速器最大变形发生在输出轴轴承孔部位和箱体左右侧部位,最大变形为0.0250 mm。减速器最大应力为48.62 MPa,小于许用应力156.25 MPa,说明强度符合设计要求,最大应力发生在齿轮箱下半部位。由此建议,优化齿轮箱结构需要对轴孔和底座部分进行加强处理。
3. 减速器箱体模态分析
3.1. 模态分析简介
模态振动是减速器箱体固有的振动属性,对减速器箱体进行模态分析得到的固有频率应当尽量避免在工作频率范围内以防止引起共振,使得减速器发生问题 [12] ,其公式如下:
(3)
式中,
是质量矩阵;
是刚度矩阵;
,
分别是位移、加速度矢量。简谐振动的位移为正弦函数:
(4)
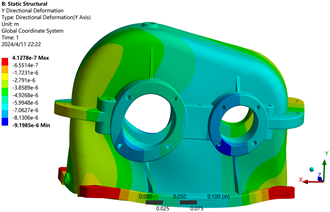
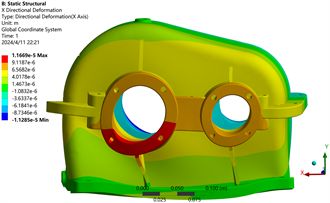
(a) X方向位移云图 (b) Y方向位移云图
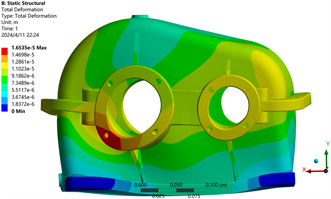
 (c) Z方向位移云图 (d) 总位移云图
(c) Z方向位移云图 (d) 总位移云图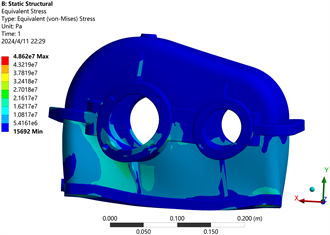
 (e) 等效应变 (f) 等效应力
(e) 等效应变 (f) 等效应力
Figure 4. Reducer case stress and strain analysis cloud diagrams
图4. 减速器箱体应力、应变分析云图
代入式得:
(5)
求解后的特征值为
,自振圆频率为对其开方后所得,得出的系统的固有频率为
。
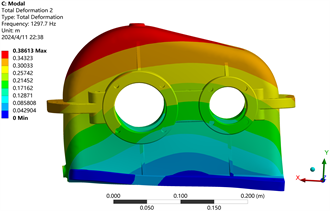
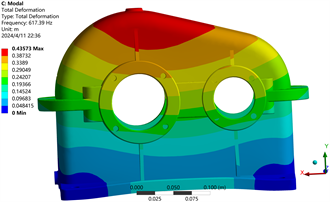
(a) 一阶 (b) 二阶
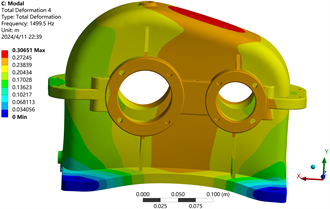
 (c) 三阶 (d) 四阶
(c) 三阶 (d) 四阶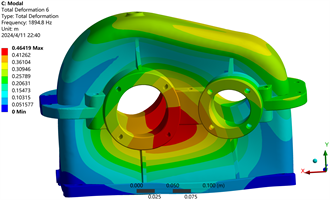
 (e) 五阶 (f) 六阶
(e) 五阶 (f) 六阶
Figure 5. The first sixth order modes of the reducer box
图5. 减速器箱体前6阶的振型
3.2. 减速器箱体模态分析
在对减速器箱体进行模态分析时,其上下箱体之间的接触为绑定约束,使用Block Lanczos法进行模态求解,提取前面六阶的模态。减速器在实际工况下,其底面被四角螺栓固定在地面上,因此需要在箱体底部添加固定约束。模态分析求解得到的减速器箱体的前六阶的固有频率及模态振型如图5所示。
表2给出了单级圆柱齿轮减速器箱体各阶的固有频率值及振型。

Table 2. The first six natural frequencies of reducer box
表2. 减速器箱体前6阶固有频率
由表2可知,减速器箱体的前6阶固有频率在617.39~1894.8 Hz之间,频率分布范围较为集中,其中第二、三、四阶模态固有频率比较接近,这与箱体结构的复杂性有关。
根据箱体振型的动画演示可以得出:1阶振型集中表现为箱体沿Z轴方向的整体摆动,以底座为中心,越向上其变动的幅度越大,容易引起连接处的疲劳损伤,需要对连接处进行加固;2阶振型集中表现为箱体沿X轴方向的整体摆动,最大变形在箱盖,对箱体的影响与1阶类似;3阶振型集中表现为箱体沿Z轴方向的向内压缩,最大变形在轴承孔位置;4阶振型集中表现为沿Y轴方向的摆动,此振型会影响减速器齿轮副的对中性,加剧齿轮的磨损;5阶振型集中表现为齿轮箱体绕Y轴方向的扭转,对箱体的影响与4阶类似,最大变形在箱体的两侧;6阶振型集中表现为齿轮箱体沿Z轴方向的局部振动。
减速器箱体的前6阶振型多种多样,这些振型会各自影响箱体的结构和强度,故对影响较大的部位需要适当的加固以减少振动对箱体的影响。
假设其减速器的输入转速为1000 r/min,按照以下公式:
(6)
将有限元分析得到的减速器箱体前六阶频率代入上式,得到不同固有频率下的减速器输入转速(n)为 [13] :
(7)
通过对上述转速进行比较分析发现:能够引起单级圆柱齿轮减速器箱体共振的转速是在37,043.4~113,688 r/min之间,减速器的实际工作转速远远低于上述转速,说明这种情况下,减速箱体几乎不会发生共振变形。
4. 减速器箱体的谐响应分析
4.1. 谐响应分析方法
谐响应分析是通过扫频分析不同频率和振幅下的结构在谐波载荷下的响应,以避免共振的发生 [14] 。其动力学的通用方程是:
(8)
式中,
是质量矩阵;
是阻尼矩阵;
是刚度矩阵;
,
,
分别代表位移、速度和加速度矢量;
是力矢量,上面的等式右侧为:
。
4.2. 谐响应仿真前处理
在模态分析的基础上,采用模态叠加法进行谐响应分析,对大齿轮孔位置施加400 N∙m的转矩,小齿轮孔位置施加200 N∙m的转矩。考虑到高频激励对减速器箱体动态响应的影响,其计算频率范围为0~2000 Hz,其施加的转矩方向如图6所示。
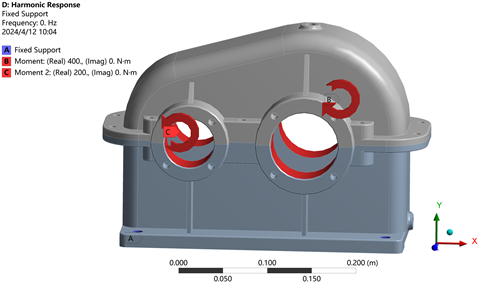
Figure 6. Applying torque to the reducer box
图6. 对减速器箱体施加力矩
4.3. 不同方向谐响应仿真结果分析
分别分析齿轮箱在X轴、Y轴和z轴方向上的响应情况,计算得到的单级圆柱齿轮减速器箱体位移—频率响应结果如图7所示。
表3给出了单级圆柱齿轮减速器箱体X轴、Y轴和Z轴方向上在各自谐振频率处所对应的振动位移最大值。
由图7和表3可以得出:
(1) 随着激励频率的增大,振动位移会在相应的谐振频率处产生峰值,其中X轴谐振频率在1297.7 Hz附近,接近减速器箱体的第二、三阶固有频率,Y轴谐振频率在1500 Hz附近,接近减速器箱体的第四阶固有频率(1499.5 Hz),Z轴谐振频率在617.39 Hz附近,接近减速器箱体的一阶固有频率(617.39 Hz),为提高寿命,其外部激励应该避免上述频率区域。
(2) Z轴方向上的振动位移要大于X轴和Y轴方向上的振动位移,X轴方向上的振动位移和Y轴方向上的振动位移相似,X轴、Y轴和Z轴方向上的谐振区间不完全一致,主要是因为减速器箱体在这三个方向上的结构差异所导致。
(3) 无论是X轴方向还是Y、Z轴方向,谐振频率较高点都在低阶频率处(0~1700 Hz),而对于高阶频率,单级圆柱齿轮减速器箱体的振动比较小,说明减速箱体对高频激励的动态响应良好。
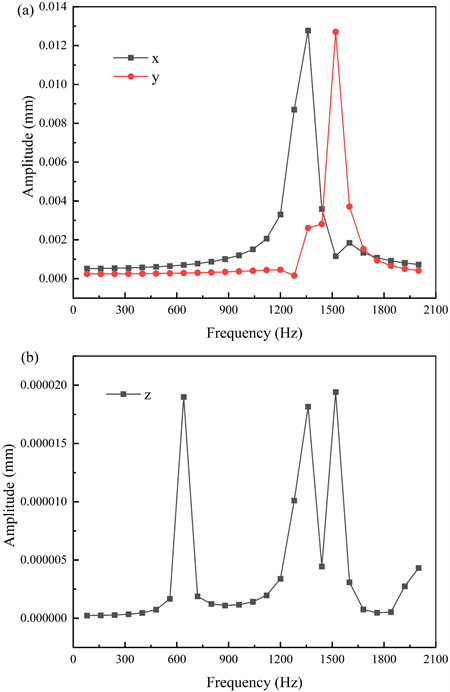
Figure 7. Displacement-frequency response of reducer box: (a) X, Y axis direction; (b) Z axis direction
图7. 减速器箱体位移—频率响应:(a) X、Y轴方向;(b) Z轴方向

Table 3. Maximum values of vibration displacements of reducer box
表3. 减速器箱体振动位移最大值
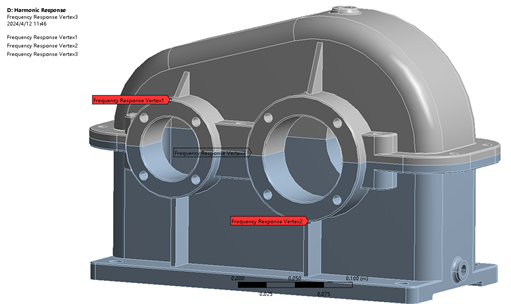
Figure 8. Nodal distribution position of reducer box
图8. 减速器箱体节点分布位置
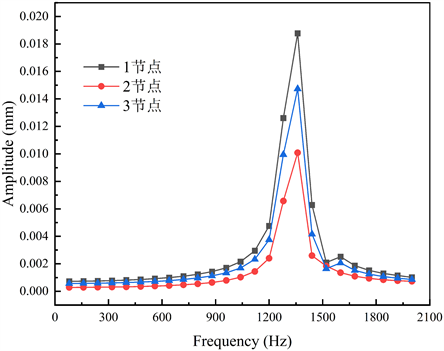
Figure 9. Displacement-frequency response at nodes of reducer box
图9. 减速器箱体节点处位移—频率响应
4.4. 不同位置谐响应仿真结果分析
为了对比分析齿轮箱在X轴方向上其箱体上不同节点的响应情况,选定了减速器箱体的三个不同位置的节点进行分析 [15] ,其中1节点位置在减速器小轴承盖上边缘,2节点位置在减速器大轴承盖下边缘,3节点在减速器箱体中间面上,其选定的节点如图8所示,计算得到的单级圆柱齿轮减速器箱体位移–频率响应结果如图9所示。
表4给出了单级圆柱齿轮减速器箱体在X轴方向上的1、2、3节点的各自谐振频率处所对应的振动位移最大值以及在1520 Hz时振动位移 [16] 。

Table 4. Maximum value of box node vibration displacement
表4. 箱体节点振动位移最大值
由图9和表4可知:
(1) 随着激励频率的增大,振动位移会在相应的谐振频率处产生峰值,其三节点处的峰值所对应的谐振频率一致,这是因为都在X轴方向上,但振动位移的最大值不同,在1360.0 Hz时,1节点的振动位移最大,2节点的振动位移最小。
(2) 通过对比三节点在1520 Hz时的振动位移可以发现,1节点在1520 Hz时振动位移出现极小值,3节点在1520 Hz时振动位移出现极小值,3节点在1520 Hz时振动位移曲线平缓。三个节点的Z轴位置相同,因此,这是由三节点的X、Y轴的位置不同导致的。
5. 结论
(1) 通过建立齿轮箱箱体有限元模型,对箱体进行静力学分析,可知该单级圆柱齿轮减速器箱体在工作过程中变形量小,且最大受力远远小于对应材料的许用应力。
(2) 通过单级圆柱齿轮减速器有限元动力学模型进行模态分析,计算得到了箱体的前6阶固有频率和振型,分析前六阶振型,得出各阶振型所对应的薄弱部分。计算结果表明,能够引起单级圆柱齿轮减速器箱体共振的转速是在37,043.4~113,688 r/min。根据计算出的减速器危险转速范围,可以尽可能的避免引起减速器箱体共振的频率范围。
(3) 对单级圆柱齿轮减速器箱体进行谐响应分析,得到其X、Y、Z轴方向上的位移—频率响应曲线,通过分析其位移幅值随频率的变化情况,发现在617.39 Hz、1297.7 Hz、1520 Hz为峰值区域,从而避免这些区域。