1. 引言
近年来安静型潜艇、无人潜航器对国家海洋国土安全带来的威胁逐渐增大,其低噪声特性和隐蔽入侵方式也给反潜行动带来极大困难。与反潜潜艇、反潜水面舰艇和反潜直升机等相比,无人反潜平台以其长期值守、封锁范围广、部署成本低等优势,成为了世界海军强国竞相发展的重要装备 [1] [2] 。无人反潜平台空投可以增加隐蔽性和突发性,可以满足快速的远距离作战需求,因而得到各国海军的高度重视。
在无人反潜平台进行空投入水的过程中,其受到的击水力是一个复杂且关键的问题。这一冲击力直接关系到平台的入水稳定性以及后续的水下操纵性能。由于入水瞬间产生的巨大冲击,不仅对无人反潜平台的结构强度和耐久性提出了高要求,还可能影响内部精密设备的功能与寿命。因此,深入研究空投无人反潜平台入水时的冲击力,对于结构的总体设计优化、提高生存性和作战效能至关重要。此外,准确的冲击力数据是进行水下弹道仿真的基础,有助于预测和分析平台入水后的动态响应和行为模式,从而优化控制策略和导航路径,确保其在复杂的海洋环境中能有效地执行反潜任务。
在空投入水冲击的研究中,国内外学者已开展大量数值仿真研究。已有的研究表明,在无人反潜平台进行空投入水的过程中,主要受到击水力的影响 [3] 。张臣 [4] 采用了近似理论先行对弹体垂直入水瞬间可能遇到的最大载荷进行了预测。在此基础上,他们进一步通过模拟仿真手段详细分析了整个空投入水过程中弹体所受的冲击情况。与此相似,李正达 [5] 等人专注于舟船空投入水时的姿态和过载特性,并通过实际的水上跌落试验来检验仿真计算的准确性。这些研究共同表明,在无人反潜平台空投入水时,击水力是影响其性能的一个主要因素,因此精确评估这一力的效应对于无人平台的设计和仿真具有极其重要的意义 [6] [7] [8] [9] [10] 。
本文通过对无人反潜平台入水过程的分析,利用数值模拟的方法对平台入水冲击的过程进行有限元仿真,对平台的入水冲击特性进行分析和研究,为无人反潜平台的总体设计提供参数支持和技术依据。
2. 入水过程分析及相关理论
2.1. 入水过程分析
无无人反潜平台入水的整个过程包括撞水、侵水、带空泡航行、全侵湿后转入受控运动等四个阶段,如图1所示。各个过程的一些主要现象和动力过程可简述如下。
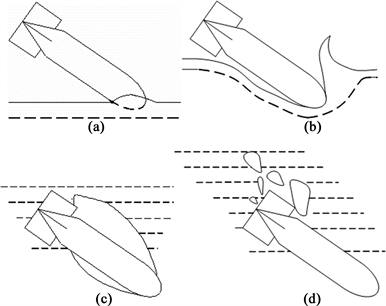
Figure 1. Diagram of the platform entering the water
图1. 平台入水过程示意图
撞水阶段(图1(a)):撞水阶段仅持续极短时间,发生在平台头部刚接触水面时,流体受头部冲击力作用产生压缩波。撞水时,平台在流体介质的反作用力下将会产生结构功能性响应,应力将会以波的形式从头部传递到尾部。由于此时头部将会遭受极大的峰值载荷,有可能造成头部局部壳体出现皱褶,对于斜入水情况,还有可能在连接处出现应力集中而造成局部破坏。尽管这一阶段平台将遭受极大的冲击压力,但由于该阶段持续作用力时间较短,且作用力面积较小,因而总的冲量相对较小,故这一阶段对平台的整体运动影响是很小的。
侵水阶段(图1(b)):这一阶段结构受到很大的流体阻力和角加速度,这不仅使壳体遭受轴向和法向过载,有可能损坏壳体结构和内部器件,而且对以后的入水弹道和入水空泡都会产生很大的影响。一旦撞水阶段结束,头部以很高的速度排挤周围的水,随着沾水面的不断扩大,水面也逐渐隆起,这时沾水面所受的流体阻力将不断增大。对于斜入水,还有可能出现“低压”及“忽扑”现象。
带空泡航行阶段(图1(c)):随着平台沾水面不断的扩大,水流开始分离并形成一个充气的空泡将结构的前半段包住。平台入水由侵水阶段转入带空泡运行阶段,此时平台所受的作用力主要为带空泡运动的流体阻力。直至空泡溃灭。
全侵湿阶段(图1(d)):当空泡溃灭,平台整个外表面被水沾湿后,进入全侵湿阶段。在这个阶段,下潜深度、平台的姿态与方位、速度的大小与方向,都将对后续的受控运行弹道产生重要影响。
2.2. 流固耦合
无人反潜平台空投入水冲击载荷仿真分析是个典型的流-固耦合问题。流-固耦合力学的重要特征是两相介质之间的相互作用,变形固体在流体载荷作用下会产生变形或运动。当物体发生变形或运动时,会对周围的流体运动产生显著影响,改变流体的负荷分布和大小。这种相互作用导致了各种不同形式的流-固耦合现象在不同条件下的出现。解决这一问题需要同时考虑流体和固体域中的变量,并使用耦合方程来描述它们之间的相互作用。这种耦合问题的复杂性在于流体和固体之间存在着不同的运动和变形特性,因此无法简单地将问题削减为单独求解流体或固体的方程。目前,人们采用整体求解方法或交替求解方法来解决这一问题。整体求解方法将流体和固体的变量作为整体来求解,但由于方程规模大、计算量大以及两者性质上的差异,这种方法可能面临较大的困难。相比之下,交替求解方法则是分别在流场和结构中进行求解,并在每个时间步之间进行耦合计算,通过耦合面来传递相关物理量来达到不同求解域的耦合,这样求解的优势就是可以充分利用现有流体及固体领域内成熟的程序,而只需加入个耦合算法就可以求解流固耦合问题,因此交替求解法越来越受到研究者的重视。
3. 基于有限元法的入水冲击特性分析
3.1. 无人反潜平台入水过程仿真
将无人反潜平台的模型简化为简单回转体,再将三维模型导入到ANSYS/LS-DYNA中进行有限元的前处理,为了减少计算时间,我们对网格数量进行了控制,并且将导入的无人反潜平台的三维模型进行有建模时,只选取平台的二分之一模型,再将平台的三维模型进行有限元网格划分,平台有限元模型图如图2所示。

Figure 2. The finite element model of mine
图2. 无人反潜平台的有限元模型
在ANSYS/LS-DYNA中建立水域和空气域的两相三维模型,并进行网格划分。空气域的模型尺寸为3000 mm × 3000 mm × 1000 mm,划分成网格后共有18,000个节点;水域的模型尺寸为3000 mm × 3000 mm × 7000 mm;划分网格后共有144,000个节点。平台以不同角度入水的有限元模型如图3所示。
3.2. 材料模型
本文中选择的单元类型是SOLID164单元。然后定义平台、水、空气的材料模型,本文中无人反潜平台的材料为铝合金5A06,水的状态方程采用Gruneisen状态方程来描述:
式中:
P表示承受压力;
V表示相对体积;
E表示单位体积内能;
为水的材料常数。
计算过程中所使用的数据如表1所示。
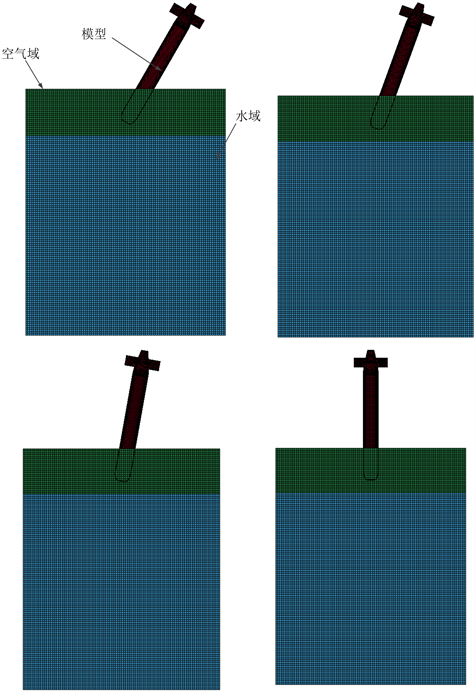
Figure 3. The finite element model of mine entering water at different angles
图3. 平台不同角度入水的有限元模型

Table 1. State equation parameter of water
表1. 水的状态方程参数
空气材料状态方程采用LINER-POLY-NOMIAL线性状态方程来描述:
式中:
P表示承受压力;
V表示相对体积;
E表示单位体积内能。
3.3. 边界条件及初始条件
当对水域和空气域进行仿真时,最好需要一个无限域来进行模拟,然而,由于用软件仿真来解决问题又是有限的。为了限制模型的规模以及减少仿真计算时间,本文使用非反射边界条件来表示无限域。通过在物体外表面创建节点的组元,然后施加非反射约束,从而可以指定沿特定的组元是否消除膨胀波与剪切波的反射。在本文中,选择空域和水域的四周以及底面上的节点组作为非反射边界条件,如下图4所示。

Figure 4. Non-reflective boundary element
图4. 非反射边界组元
4. 入水冲击载荷计算结果与分析
计算不同高度、速度和姿态情况下平台入水冲击载荷和空泡特性。本文研究的入水高度为10~200 m,根据自由落体原理可以分析出无人反潜平台在200米高度下降到水面时的速度为63 m/s。本文开展了入水速度20~60 m/s,入水角度60˚~90˚不同组合下的入水冲击载荷计算。
4.1. 不同速度入水时的计算分析
首先分析不同姿态下入水速度对入水冲击载荷的影响。分析过程中,分别计算了平台的轴向冲击载荷与法向冲击载荷随时间的变化趋势。
以下是20 m/s、40 m/s、60 m/s几种入水速度下的计算结果。
由图5~7不同入水速度下的计算结果,可以得到如下结论:
(1) 无人反潜平台斜入水时,从平台触水开始,入水冲击载荷逐渐达到最大峰值,并且平台斜入水时载荷峰值到达时间比平台垂直入水时载荷峰值到达时间长,大概在入水后3.5 ms左右;
(2) 无人反潜平台斜入水时,平台的入水冲击载荷在最大峰值之后减小,轴向载荷在达到最大峰值后
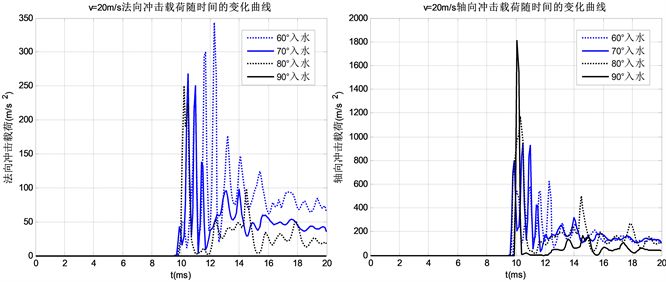
Figure 5. The normal and axial impact when the entering water speed is 20 m/s
图5. 入水速度为20 m/s时法向冲击和轴向冲击变化曲线
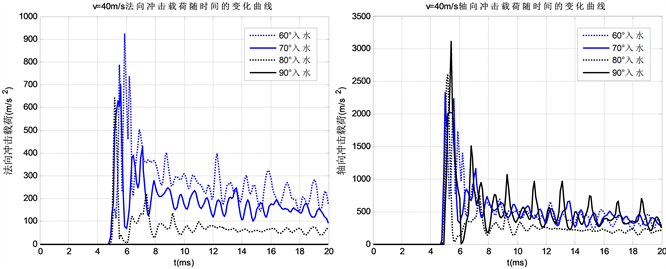
Figure 6. The normal and axial impact when the entering water speed is 40 m/s
图6. 入水速度为40 m/s时法向冲击和轴向冲击变化曲线
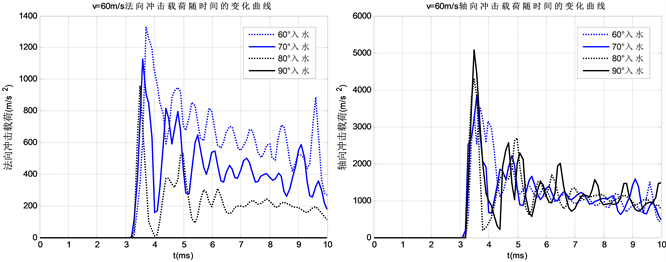
Figure 7. The normal and axial impact when the entering water speed is 60 m/s
图7. 入水速度为60 m/s时法向冲击和轴向冲击变化曲线
维持在一个较低的数值,径向载荷在达到最大峰值后迅速减小,并且最终在低值附近震荡;平台受到的冲击载荷主要为轴向载荷,且对平台强度影响较大;
(3) 无人反潜平台垂直入水时,在平台入水冲击的初期,入水冲击载荷达到最大峰值,即在平台入水0.5 ms内冲击载荷达到峰值;
(4) 无人反潜平台垂直入水时受到的冲击载荷远大于斜入水时受的冲击载荷。
4.2. 不同角度入水时的结果分析
对无人反潜平台以不同角度入水时的冲击载荷进行研究,获取平台承受冲击载荷呈现不同的特性。分析过程中,分别研究了60˚~90˚时,不同入水角度下的轴向冲击载荷与法向冲击载荷特性。
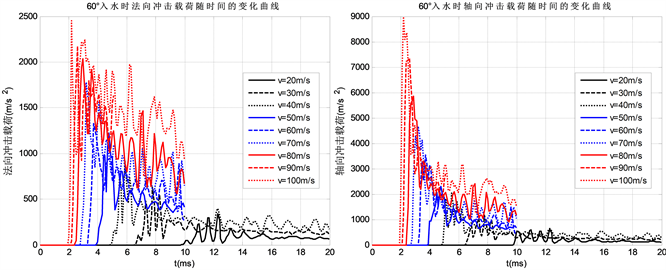
Figure 8. The normal and axial impact when the entering water angle is 60˚
图8. 入水角为60˚时法向冲击和轴向冲击变化曲线
从图8、图9可以看出,无人反潜平台同一入水角度下,速度越大,结构受到的冲击载荷越大,同时结构局部的压力峰值也会增大。因此无人反潜平台入水前要避免过高的速度,在入水前必须采取适当的减速和保护措施。对于减速方式,工程上一般采用降落伞的方式,但是此法的弊端在于入水前平台的姿态不易控制;在不显著降低入水速度的情况下,还可采用其他缓冲保护方式,如采取尖拱型缓冲头帽的方式,可以有效地降低入水载荷,同时入水时平台的姿态不会发生太大改变。
表2为不同入水速度、角度时法向与轴向载荷峰值的汇总。
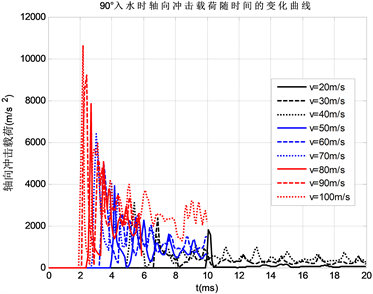
Figure 9. The axial impact when the entering water angle is 90˚
图9. 入水角为90˚时轴向冲击变化曲线

Table 2. The normal and axial peak impact at the different speeds and different angles
表2. 不同入水速度、角度时法向与轴向冲击峰值
5. 结论
本文利用数值模拟的方法对无人反潜平台的入水冲击特性进行分析和研究,结果表明:
1) 空投无人反潜平台入水时,随着入水速度的增加,作用在平台壳体上的冲击载荷也随之增加,冲击载荷峰值巨大,这对平台壳体的强度尤其是头部结构强度提出了极高的要求。因此,有必要尽可能降低空投无人反潜平台入水时的速度。
2) 速度相同的情况下,无人反潜平台垂直入水时受到的冲击载荷远远大于斜入水时受的冲击载荷,选取合适的入水角度(如60˚)可减小平台的入水冲击力。
本文通过数值模拟手段对无人反潜平台入水冲击特性进行了深入分析,研究结果凸显了入水速度和入水角度两个关键因素对于平台结构尤其是头部结构强度设计的重大影响。研究结果不仅对无人反潜平台的设计与结构优化具有指导意义,也为其安全运行和任务执行效率的提升提供了重要参考。