1. 引言与文献综述
随着近年来互联网技术的快速发展,涌现出很多贷款模式,比如b2C贷款、P2P贷款、P2C贷款等。这些贷款模式的出现给人们带来方便的同时也增加了相关金融机构的风险压力,金融机构只有精确地对个人进行信用评估后才能降低贷款的风险。然而,个人信用由多方面因素组成,其中就包括个人基本信息、信贷记录、个人财产等。因此在复杂的因素环境中设计出一个好的信用评估模型对于金融机构来说具有重要的意义。
常用于构建信用评估模型的机器学习方法有朴素贝叶斯(NB)、多元回归分析、逻辑回归、神经网络等。比如朱毅峰等提出了融合BP神经网络和概率神经网络的微型企业信用评估模型,实验结果表明该模型能够降低对差企业的误判率,具有重要的实际价值意义 [1] 。姜明辉等利用多元回归分析方法建立了是否获得贷款和其他变量的关系,基于该方法能够较为准确的判断是否给个人发放贷款 [2] 。张国政等使用逻辑回归模型分析了商业银行的信贷数据,研究发现影响个人信用的关键因素主要有贷款金额、婚姻状况等六项指标 [3] 。李旭升等在信用评估的实验中对比了David West的五种神经网络和三种NB算法,结果表明NB算法具备更好的信用评估能力 [4] 。
其中NB算法因其扎实的概率论基础、简单的模型结构和稳定的分类能力等优点,在很多分类任务中得到了广泛的应用。然而NB算法需要满足特征之间独立,这在现实中很难满足,往往是特征之间越不独立,其分类效果就越差。针对此问题,模型融合是一种有效克服特征独立性假设问题的策略。比如叶晓枫等首先通过随机森林算法对信用数据集提取特征,然后用NB算法训练所提取的特征,研究表明此两种算法的融合能够提高信用预测精度 [5] 。徐屾等从三个不同角度提出了三种改进的NB信用评估模型,并在其实验中取得较好的评估效果 [6] 。秦锋等将快速独立分量分析(FastICA)与NB算法融合得到FastICA-NB模型,该模型将原始样本投影到独立的特征空间,从而获得具有独立性的新样本,进而改善分类效果 [7] 。李楚进等针对独立性要求采用PCA的改进方法得到了融合的PCA-NB模型,该模型将原始特征变换为不相关特征,提高了NB的分类效果 [8] 。
独立分量分析(ICA)作为盲源分离的一种重要统计方法,最大特点就是通过其处理后的数据具备独立性,能够满足NB算法对特征独立性的要求。随着ICA的快速发展,学者们已经提出很多种ICA的变体,其中用得最多的当属HyvarinenAapo提出的FastICA [9] 。线性判别分析(LDA) [10] 作为一种降维方法,优势在于它是一种有监督学习方法,经其降维后不同类别的样本尽可能分开。
综上所述,结合FastICA和LDA的优势,提出一种基于模型融合改进的NB分类算法——FastICA-LDA-NB。将所提模型应用于UCI上的德国个人信用数据集,实验结果表明FastICA-LDA-NB具有较好的个人信用评估能力。
2. 相关理论基础
2.1. 朴素贝叶斯算法
假设分类任务的输入特征为n维向量
,输出类别
,则朴素贝叶斯公式为:
(1)
考虑到
对所有类别都相同,因此式(1)可转化为如下NB算法的学习模型:
(2)
由式(2)可得,朴素贝叶斯分类的学习意味着估计
和
。设N表示样本总数,由极大似然估计得到两个概率值为:
(3)
(4)
其中ail表示第i个特征
在集合
中的第l个值,
;
;且n表示特
征总数,Si为特征
取值集合的大小。式(3)和(4)中概率估计值的分子可能会出现零,对后验概率计算产生影响。可采用贝叶斯估计解决该问题,即式(3)、(4)分别修改为:
(5)
(6)
其中
,特别地当
时为拉普拉斯平滑。
2.2. 独立分量分析
ICA是信号处理领域的一种统计方法,其主要任务是把混合信号分解成若干个独立的信号。图1为
ICA模型的简单表示,其中
为n维未知独立成分,一般假设该n维分量的均值为0方差为1,A为
维的未知混合矩阵,
为m维观测变量,W为解混矩阵,ICA的主要任
务是求解矩阵W,使得输出
是S的最佳逼近。

Figure 1. Simple block diagram of independent component analysis
图1. 独立分量分析简单框图
评价Y中各分量独立性的常见准则有信息最大化、负熵最大化等。基于这些评价标准,衍生出了很多ICA的实现方法,比如JADE、FastICA [11] 等。本文采用负熵最大化的FastICA,负熵定义为:
(7)
其中
表示Y的熵,
为Y的密度函数,
是与Y具有相同协方差阵的
高斯随机变量,负熵一般近似为:
(8)
是一个非二次函数,常用的形式有如下三个 [12]
(9)
其中a通常取区间(1,2)的常数。
要使(7)式最大,只需
最大,根据Kuhn-Tucker条件,在
条件下,当
最大时有:
(10)
式中
为恒定值,
,由牛顿法对式(10)求极大值得W的迭代式为
(11)
求出W之后,根据
便可得出独立成分S的估计。
2.3. LDA降维
LDA是一种监督降维方法,其核心思想是通过广义特征值分解把高维特征映射到低维特征,使得在
低维特征空间中的异类样本尽可能分离。设N为样本总量,K为类别总数,Nk为第k类样本量,
为第k类样本均值向量,
为全体样本均值向量,
为类别k中第j个样本。LDA的计算步骤如下:
a) 计算第k类样本的协方差阵
(12)
b) 计算类内散度矩阵
(13)
c) 计算类间散度矩阵
(14)
d) 计算
的前d个特征值对应的特征向量,组成投影矩阵W
e) 计算训练样本X降维后的特征数据
2.4. FastICA-LDA-NB信用评估模型
结合FastICA能够分离出独立分量以及LDA算法作为有监督降维的优势,将FastICA与LDA的结合作为NB算法的预处理系统,提高了NB算法在信用评估中的性能。FastICA-LDA-NB信用评估的设计流程如图2:
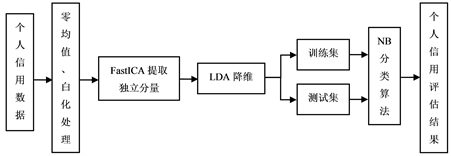
Figure 2. FastICA-LDA-NB credit evaluation process
图2. FastICA-LDA-NB信用评估流程
FastICA-LDA-NB模型的信用评估过程如下:
a) 对信用数据进行零均值、白化处理,使得模型在提取独立分量阶段取得更好的收敛性。
b) 通过FastICA方法提取独立分量。
c) 利用LDA对所提取的独立分量进行降维处理。
d) 对降维后的数据随机划分为训练集和测试集。
e) 利用训练集训练NB算法模型。
f) 使用训练后的NB算法对测试集测试,从而获得个人信用评估结果。
3. 实验与结果分析
3.1. 实验数据与评价指标
本文选取UCI上的德国某银行信用卡个人信用数据集german.data-numeric,该数据集由700个信用好的用户和300个信用差的用户组成。每个样本由客户的信用账户额度、年龄、资产状况等24个特征组成。该数据集质量好,不存在缺失情况。
为了比较各模型的信用评估效果,选取准确率P、召回率R作为评价指标。各指标的具体计算公式为
(15)
其中TP、TN、FP、FN分别表示真正例、真反例、伪正例、伪反例。
3.2. 实验过程
对于模型选取:为了验证提出模型的可行性,采用python编程语言实现各个模型,以NB、PCA-NB、FastICA-NB和RF-NB四个模型作为参照模型,比较FastICA-LDA-NB模型在信用评估中的效果,每个模型重复50次实验。
对于各模型参数:FastICA中的
函数形式选取式(9)中的
形式、
,解混矩阵W随机
初始化;PCA中主成分的选取原则为特征值贡献率大于90%;RF中决策数为500个、决策树最大深度为5。
对于数据集划分:每次实验随机划分训练集和测试集,其中测试集占20%。
3.3. 实验结果与分析
为了更直观地了解各模型的分类效果,画出了50次实验中准确率P、召回率R两个指标的箱线图,如图3、图4所示:
对50次实验后的P、R取平均得表1:

Table 1. Comparison of P and R indicators of five models (%)
表1. 五个模型的P、R指标比较(%)
从上面图3、图4的箱线图可以看出,在50次实验中所提模型FastICA-LDA-NB的两个评价指标P、R整体上优于NB、PCA-NB、FastICA-NB和RF-NB四个模型。由表1得出提出的模型较其他四个模型在准确率P上提高了大约2.5%~6.5%,在召回率R上提高了大约3.5%~4.5%,表明FastICA-LDA-NB模型在个人信用评估中有较好的实用性。
由FastICA-LDA-NB与FastICA-NB对比可以看出引入LDA进行降维的恰当性,充分利用了LDA属于有监督降维的优势。FastICA-NB相对于NB来说没有提升精度,可能是提取独立分量后的特征存在信息冗余造成的,因为经过特征降维或特征选择处理后的PCA-NB和RF-NB两种模型均较NB来说有所提高。
FastICA能够分离出相互独立的特征,刚好满足NB算法的独立性假设。但是不确定分离出来的特征对分类任务的重要性,如果存在特征冗余问题,那么反而会降低NB算法的分类准确率。所以本文有机结合了FastICA、LDA和NB的优势,构造了FastICA-LDA-NB模型,并取得较好的实验效果,因此在个人信用评估领域有一定的价值意义。
4. 结语
构建科学的信用评估模型,可以帮助银行等金融机构更加准确地判断客户信用状况,进而作出合理的决策,有效避免了风险。目前NB算法被广泛应用于信用评估领域,但其对属性独立性假设的要求很难满足。因此本文应用了盲源分离领域的FastICA算法,该算法能够分离出具有独立性分量,恰好满足NB算法的要求。考虑到数据集存在特征冗余的情况,在FastICA的基础上引入LDA,该方法属于有监督降维,降维后的特征能够使不同类别之间的样本尽可能分离。综上所述,本文综合利用了FastICA、LDA和NB三者的优势,提出了FastICA-LDA-NB的信用评估模型。在德国个人信用数据集上的结果表明,提出模型不仅提高了NB算法的分类精度,而且与文献中几种NB的融合模型相比也取得较好的分类效果,表明了FastICA-LDA-NB模型对于提高金融机构的风险管理具有一定的意义。
此外,本文提出模型虽然有所改善,但准确率P和召回率R的提升幅度不够大,仍有提升的空间。下一步研究将会考虑深度学习中的表征学习思想,把FastICA-LDA-NB集成具有深层结构的模型,使其能够充分挖掘信用数据中的信息,进而构建更加科学的信用评估模型。
基金项目
国家自然科学基金项目(11771321);山西省社会发展科技攻关计划项目(201703D321032)。
NOTES
*通讯作者。