1. 引言
生物资源的开发利用是学术界的一个经典问题。在这个经典问题上,人类不仅考虑短期的经济利益,更注重生物资源的可持续利用。毫无疑问,最大的问题之一是如何设计一个可接受的开发解决方案。从大型生物种群到特殊生物种群,许多学者对其进行了研究。例如,在 [1] 中,Li和Wang研究了一般随机Logistic人口模型中基于最大可持续产量和最大留存利润两个管理目标的最优控制策略。Messaoud和Lotfi [2] 研究了各种渔业种群的确定性模型,有一般的Logistic模型和显示Allee效应的模型。通过优化和数值计算,确定了不同种群密度下的最大产量。在 [3] 中,Ding和Suzanne利用包含半线性椭圆偏微分方程、Dirichlet边界条件和Logistic种群增长的显式空间模型研究了一个最优渔业捕获问题。考虑两个目标函数:最大产量和最小成本或捕捞努力量的变化(控制)。建立了两种条件下最优收获控制的存在性、必要条件和唯一性。给出了诺伊曼(无通量)边界条件下产量最大化的结果。最优控制用变分不等式表示。
然而,自然界的各种噪音成为研究这些问题的不确定因素,如自然灾害,全球变暖,金融危机的影响,如股票和债券。因此,随机控制策略的研究受到了更多学者的青睐。J.R.和R.M.在Science [4] 上首次研究了随机波动环境下的收获种群。Li等人 [5] 研究了一种单种群模型的最优控制策略,该模型的收获努力和固有增长率受高斯白噪声影响。Liang等人 [6] 利用导出的近似Fokker-Planck方程研究了噪声和相关加性色噪声的稳定强度分布,以及包含相关泵浦噪声和颜色量子噪声的单模激光立方体模型。Jin等 [7] 研究了由颜色相关的颜色噪声驱动的标准双稳态Duffing模型的稳态概率密度函数、状态变量的均值和方差。噪声的参与使得最优控制问题更加复杂,并且使种群研究的不确定性增大,更有可能产生许多无法预料到的结果,这导致人们在实际生活中总是想办法避免噪声的干扰,但随着现代技术的发展,对随机噪声进行适当的干预和引导反而会在种群系统的研究中产生更加积极的作用,比如在这一章中,共振激活现象的发生,随机共振,噪声诱导下的相变情况,所以噪声在种群随机动力学的研究中扮演者一个非常重要的角色。
2. 模型分析
种群竞争模型可以用来描述两个种群之间的竞争过程,并分析产生不同结果的条件。例如,对于一个群体,当它独自生活时,其量的变化服从逻辑规律。本文采用经典的logistic种群模型作为研究对象:
(2-1)
式中,
为t时刻的种群密度,K为环境承载力,r为种群增长率。Logistic生长模型又称迟滞生长模型,是一种常见的生物种群生长模型,包括从单细胞生物到高等生物的许多生物种群。该模型表明,种群增长率应该与种群数量有关。这种类型的种群模型已经被研究过 [8] [9]。
在控制模型的这一部分研究中,我们遵循以下假设:
1) 自然和人类社会中的噪声都是乘性和加性的,分别由白噪声和色噪声产生。
2) 在以下假设下,种群资源受到开发。
其中h是一个严格递增的函数,
,E表示捕获努力量。E指捕鱼规模或数量,人们投资,资源组在一定海域或水域内一段时间(年,月或鱼洪水,等等),它反映了捕获的资源组的死亡水平,生物学意义的E也适用于其他种群。这样,捕获种群的方程式就可以写作:
(2-2)
3) 时间范围是无限的,没有任何折现因素。
设(2-2)中
,得到一个非零平衡解
可持续的收益是
令
,
,那么
有一个最大点
,最优捕获努力量
为
当
时,最大可持续产量为
此外,我们可以证明最大可持续产量
是渐近稳定的,无论何时有小扰动,然后随着时间的推移
被恢复。事实上,我们有
(2-3)
则由式(2-3)得到
的渐近稳定性。
接下来,我们为模型引入随机噪声。在该系统中,引入的噪声分别为加性噪声和乘性噪声。加性噪声通常来源于内部噪声,而乘性噪声通常来源于外部噪声。现在考虑一个由加性噪声和乘性噪声驱动的种群模型,这个模型可以表示为如下的方程:
(2-4)
(2-5)
其中,
和
为高斯白噪声
(2-6)
这里,
为指数型高斯色噪声
(2-7)
其中,D和
分别为乘性高斯色噪声强度和加性高斯白噪声强度,
为乘性色噪声的噪声强度。
3. 稳态概率密度函数
3.1. 稳态概率密度函数的推导
我们可以将模型(2-4)写作如下形式:
(3-1)
对应式(3-1),这里
(3-2)
将扩展的UCNA应用到相关噪声的情况下,由(2-4)-(2-7)得到下列一维马尔科夫过程:
(3-3)
将(3-2)带入得:
(3-4)
在这里
化简得
(3-5)
为了从(3-4)和(3-5)中得到FPK,我们从随机等价的Stratonovich随机微分方程出发
(3-6)
其中
(3-7)
这里
是高斯白噪声
(3-8)
(3-3)和(3-6)的随机等价性证明类似于 [4]。
为了便于后续研究,我们将(3-6)写成如下形式
(3-9)
其中
(3-10)
根据文献 [10],(2-1)的势函数为
存在两个稳定性点:
,
,通过诺维科夫定理和均匀有色噪声近似(UCNA),对应的FPK方程为
(3-11)
其中,漂移函数和扩散函数的表达式分别为:
式(3-11)中,漂移系数和扩散系数都与t无关,因此FPK方程必须有稳态解。在FPK的研究中,稳态解的研究更为重要,原因是稳态解反映出了系统的持续性行为。在经过各种不同长度的瞬态过程后,系统将受到这种长时间行为的支配。因此,人们在大多数时候测量的正是这种稳态解的性质。同时,我们将看到FPK的稳态解也与确定性方程的某个势函数有关。该势函数作为平衡系统的拓展,将其称之为广义势函数。广义势函数既决定了系统的静态特性,又决定了FPK的确定性方程和一些重要的动态特性。
模型(2-4)的稳态密度函数
可由 [4] 给出:
(3-12)
这里,
为归一化常数。
根据密度函数归一性的性质,可得:
那么
稳态概率密度函数也可以用如下形式来表示:
(3-13)
是有效势函数。
通过计算可得:
(3-14)
3.2. 讨论与生物解释
接下来,我们讨论稳态概率密度函数分别受乘性色噪声强度D、加性白噪声强度
和相关时间
影响的变化曲线图,并结合生物学意义对呈现的图象进行解释说明,进一步归纳出重要的结论。
图1描述了当乘性高斯色噪声强度D取不同值时,种群稳态概率密度函数的变化曲线图。图象呈单峰结构,峰值在
附近取到,并且随着乘性色噪声强度的增加,峰值高度在降低;在
处,曲线所占比例随乘性噪声强度的增强而增大,当D取最小值时,曲线在
处的取值几乎为零;当x增大到一定程度时,D取不同值的曲线变化趋于一致,表明此时稳态密度函数受乘性噪声强度D的影响变小,无论乘性噪声强度如何变化时,稳态概率密度函数的变化都是一致的。结合种群的生物学意义可知,乘性噪声强度D的增加不利于种群生存,会增大种群灭绝的可能性。
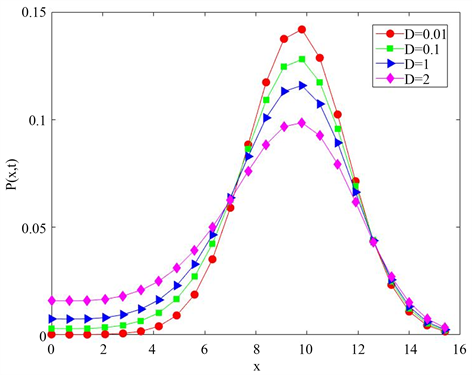
Figure 1. The relation between
and x under Gaussian color noise intensity
图1. 高斯色噪声强度下
和x的关系
图2描述了当加性高斯白噪声强度
取不同值时,种群稳态概率密度函数的变化曲线图。曲线呈单峰结构,峰值在
处取到,并且随着加性白噪声强度的增加,峰值高度在降低;在
两侧并且远离K值时种群的密度函数趋向于零,说明此时种群处于完全灭绝状态。由此可以得出结论,种群内部加性噪声强度的增加不利于种群生长,这与种群密度函数受乘性噪声强度影响的变化规律是一致的。
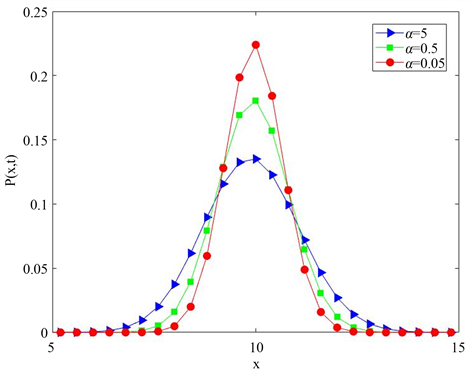
Figure 2. The relation between
and x under Gaussian white noise intensity
图2. 高斯白噪声强度下
和x的关系
图3描述了相关时间
取不同值时,种群稳态概率密度函数的变化曲线图。曲线呈双峰结构,峰值分别在
,
处取得。当
增加时,曲线的左峰降低,右峰升高;当
减小时,密度函数的左峰升高,右峰降低。由图可以得出,乘性噪声强度相关时间的增加有利于种群的生存,而且可以推测出相关时间越大,种群的生长趋势越好。
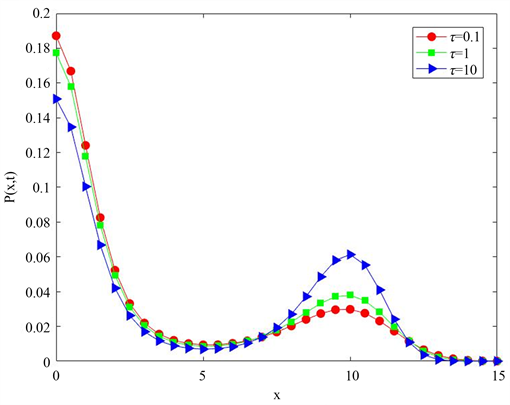
Figure 3. The relation between
and x at relevant time
图3. 相关时间下
和x的关系
4. 平均首次穿越时间
4.1. 平均首次穿越时间的推导
为了进一步研究这个模型,这里我们估计了一个种群从一个稳定状态移动到另一个稳定状态所需的时间。这量化了噪声对稳态之间过渡的影响。这个时间叫做初渡时间。经过多次试验,我们可以得到平均首次穿越时间。如果从一个初始稳定态到另一个初始稳定态的平均首次穿越时间较长,说明初始稳定态 [11] 相对稳定。在这里,我们应该关注种群从稳定状态
到稳定状态
的平均首次穿越时间的表达式 [12] [13] [14] [15]。
(4-1)
这里,T可以通过最陡下降近似 [16] 得到
(4-2)
在这种情况下,
是有效势对x的二阶导数。
通过计算得:
(4-3)
4.2. 讨论与生物解释
根据公式(4-3),接下来研究了平均首次穿越时间分别受乘性色噪声强度D、加性白噪声强度
和相关时间
影响的变化曲线图,并结合种群的生物学意义对图像进行解释说明,归纳出较为一般的结论。
图4描绘了乘性噪声强度D对平均首次穿越时间的影响。我们在这个图象中可以观察到,随着加性噪声强度
的增加,曲线先减小后增大。当乘性噪声强度D很小时,平均首次穿越时间受
的影响较大,而当乘性噪声强度D增大时,平均首次穿越时间受
的影响较小。我们还发现当
增强到一定程度时,会发生共振激活现象。共振激活现象是生物学中一个很关键且重要的结论,对于研究随机噪声干扰对种群系统的影响作用有很大意义。通过这幅图像再结合种群的生物学意义可以得出:平均首次穿越时间的行为对较小的乘性色噪声强度比较敏感,而受较大的乘性色噪声强度的影响较小 [17]。

Figure 4. The relationship between MFPT and multiplicative color noise intensity
图4. MFPT和乘性色噪声强度的关系
图5描绘了加性噪声强度
对平均首次穿越时间的影响。当
和
时,随着乘性噪声强度D的增加,平均次穿越时间的曲线先降低后逐渐变平缓。当
和
时,曲线先上升后变平缓。但曲线最终都会以稳定状态结束。这表明,平均首次穿越时间对较小的乘性色噪声强度更敏感,此时平均首次穿越时间受乘性噪声强度的影响较大。而当乘性噪声强度增大到一定值时,乘性噪声强度的变化对种群平均首次穿越时间的影响很小,平均首次穿越时间值几乎没有什么变化。
结合图4和图5,可以得出,平均首次穿越时间的行为对较小的乘性噪声强度更敏感。当乘性噪声强度较大时,加性噪声强度的变化对稳态穿越时间的影响较小。还有一个很重要且很关键的结论是,当加性噪声强度
达到一定水平时,共振激活现象 [18] 发生。生物系统极其复杂,噪声强度对种群的影响也受到其他参数的限制。当加性噪声强度较小时,乘性噪声强度的增加会对种群的生存和稳定产生不利影响。然而,当加性噪声强度相对较大时,乘性噪声强度的增加将对种群的稳定和发展起到积极作用。这一结论为我们在实际生活中探究种群噪声强度对平均首次穿越时间的影响提供了重要的理论支撑。
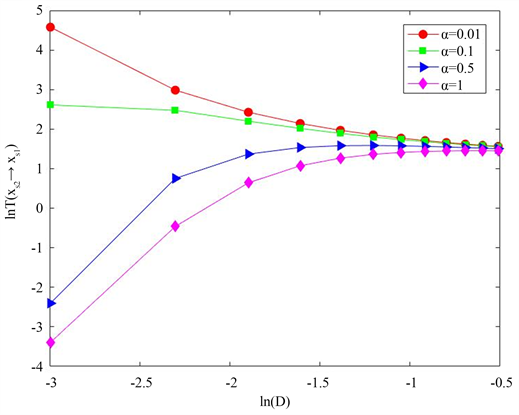
Figure 5. The relationship between MFPT and additive white noise intensity
图5. MFPT和加性白噪声强度的关系
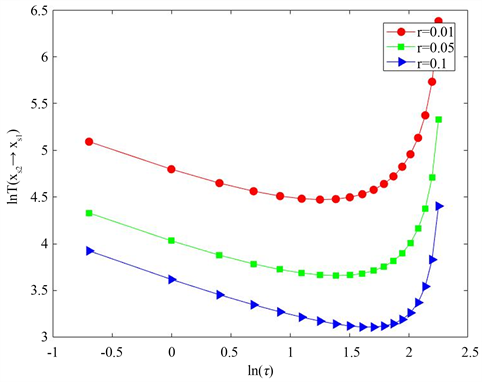
图6描述了不同增长率r对平均首次穿越时间的影响。两幅图的曲线都呈先下降后上升的状态,当r增大时,共振激活现象再次发生。图6(a) 中,在共振激活现象发生之前,固定
值,增长率r的增加有助于平均首次穿越时间的加速。在这里,时间的加速意味着种群灭绝的可能性增加。与图6(a)不同的是,图6(b) 的曲线先相交后出现共振激活。因此,在图6(b)中,将
值固定,增长率r的增加使得平均首次穿越时间变得缓慢,时间的缓慢意味着种群灭绝的可能性降低。曲线相交后,增大r对平均首次穿越时间的影响与图6(a)相同。
由图6可以得出,增长率对种群的影响不是恒定的 [19],它受到各种影响因素的制约。当增长率较低时,它的增长不利于种群内的繁殖。但当增长率上升到一定水平时,它的持续增长将有利于种群的生存。所以,在对平均首次穿越时间受种群增长率的影响进行研究时,要考虑全面,充分认识到增长率对种群生存影响的不稳定性,而不可片面的下结论。
5. 结论
本文的创新点在于模型中的参数受到的外部环境随机干扰不同,即建立的模型中的参数有别于前人所研究的。首先,我们引入了一个带有高斯色噪声和高斯白噪声的种群模型。然后,利用统一色噪声近似(UCNA)法推导了种群的稳态概率密度函数和平均首次穿越时间的表达式。紧接着还讨论了不同变量对密度函数的影响以及对种群从一个稳态到另一个稳态所需的时间的影响,再结合种群的生物学意义进行绘图并解释。
 (a)
(a) (b)
(b)
Figure 6. The relationship between MFPT and relevant time
图6. MFPT和相关时间的关系
研究表明,不同的噪声强度对密度函数有不同的影响。通过比较不同噪声强度对稳态概率密度函数的影响,发现概率密度函数受加性噪声强度的影响较小,而受乘性噪声强度的影响较大。在相关时间对密度函数的影响中,出现了双峰结构。更重要的是,当研究乘性噪声强度对平均首次穿越时间的影响时,当加性噪声强度不断增加,并且达到一定程度时,就会发生共振激活,在发生共振激活时,当乘性色噪声的强度增加到一定大小时,跃迁会被抑制。在种群增长率对相关时间的影响中,得出低增长率对种群存活有不利影响,而高增长率促进种群生存。
有待进一步研究的问题:文中我们假设噪声影响
,除此之外,噪声还可能影响模型中的其他参数。即噪声影响其它某个参数也能够精确地模拟种群受到的随机干扰,并且由此得出的种群模型不同,对于后续的研究结果也会出现很大的变化。
致谢
非常感谢我的导师李东喜副教授。从论文的构思,撰写再到修改,定稿,李老师多次进行了认真指导,更是提出了很多中肯贴切的意见和建议,是一位认真负责的好老师。李老师对待学术求真务实,一丝不苟,对待工作勤奋踏实,兢兢业业,值得我们学习。在此向他致以诚挚的谢意。
其次,感谢给予转载和引用权的文献及研究思想和设想的所有作者,正是借助你们的肩膀,我才能够更好地完成论文的撰写。
NOTES
*通讯作者。