关于部分标定简单图的数目

On the Number of Partially Labelled Simple Graphs

摘要: 本文讨论部分标定简单图的数目，首先介绍了计算标定简单图的公式，然后确定了当顶点个数为3时的标定简单图的数目为8个。主要证明了当顶点个数为4时的标定简单图的计数以及所有画法，并用数学方法证明了它的数目的精确值为64。最后也给出当顶点个数为4时，非标定简单图的数目为11个以及全部画法。近百年来，国内外很多学者都对这一问题进行了研究。由于所涉及的画法较多并且证明过程较为复杂，国内外关于此领域的研究进展缓慢。相比较而言，本文给出了四个顶点的标定简单图的所有画法，并采用度序列的方法更简洁直观，更具创新性。

Abstract: In this paper, we discuss the number of partially labelled simple graphs. First, the formula for cal-culating the calibrated simple graphs is introduced. Then, when the number of vertices is 3, the number of calibrated simple graphs is determined to be 8. This paper mainly proves the counting and all the drawing methods of the labeled simple graph when the number of vertices is 4, and mathematically proves that the exact value of its number is 64. Finally, when the number of vertices is 4, the number of uncalibrated simple graphs is 11 and all the drawing methods are given. Over the past century, many scholars at home and abroad have studied this issue. Due to the many drawing methods involved and the complicated proof process, the research progress in this field at home and abroad is slow. In comparison, this paper gives all the drawing methods of the simple graph of the four vertices, and the method of degree sequence is more concise, intuitive and innova-tive.

1. 引言

拓扑图论作为图论的一个分支，这个问题的最初研究起源于1736年欧拉提出的著名的欧拉公式 [1]，其关注的是如何在平面上表示图。图之所以如此命名是因为它们可以用图形来表示，正是这种图形表示帮助了我们理解它们的许多性质。现实世界中的很多情况都可以通过一个由一组点和连接这些点对的简单曲线组成的图来描述，有趣的哥尼斯堡桥问题以及其它的一些实际问题都涉及到图论 [2]。

在关于图论的历史研究中，很多结论与猜想都是围绕着一些特殊图类进行的。本论文对部分标定简单图的数目进行了研究，介绍了关于图论的相关基础知识，并给出了如何计算标定简单图的数目的公式，分别确定了当变量为3和4时的标定简单图的精确值及全部画法，也确定了当变量为4时的非标定简单图的精确值及全部画法。

2. 预备知识

避免在本文的相关讨论中产生歧义，首先介绍图论的一些理论并将这些提及的理论应用于本文所研究的问题中。

2.1. 图的定义和表示

定义1图G是一个有序对(V(G)，E(G))，这个有序对由一个顶点集V(G)和一个与V(G)不相交的边集E(G)组成。同时，它还与一个关联函数ψ_G相关联，此关联函数ψ_G将G的每一条边映射为G的顶点集V(G)中的无序点对。如果e是G的一条边，u和v是G的两个顶点，那么ψ_G(e) = {u, v}称为e连接了u和v (为了简化，可将无序对{u, v}记作uv)，顶点u和v被称为e的端点 [3]。

在图G中将顶点集的数量记为v(G)，将边集的数量记为e(G)，这两个基本参数分别称为G的阶数和大小。若一个图的顶点集合为空集，则称它为空图。

例如，G = (V(G), E(G))，令

$V\left(G\right)=\left\{u,v,w,x,y\right\}$

$E\left(G\right)=\left\{a,b,c,d,e,f,g,h\right\}$

ψ_G被定义为

${\psi }_G\left(a\right)=uv$， ${\psi }_G\left(b\right)=uu$， ${\psi }_G\left(c\right)=vw$， ${\psi }_G\left(d\right)=wx$

${\psi }_G\left(e\right)=vx$， ${\psi }_G\left(f\right)=wx$， ${\psi }_G\left(g\right)=ux$， ${\psi }_G\left(h\right)=xy$

此时，v(G) = 5，e(G) = 8。

2.2. 图的画法

在一个平面上，一个图的画法是从该图形到平面的一一映射，简记为D。此映射将图的每一个顶点映射为平面上的点(为清晰起见，顶点用小圆圈表示)，并通过连接其端点位置的简单曲线来表示每条边。

D的顶点的全体记作V(D)，D的边的全体记作E(D)。

2.3. 交叉与交叉数

设D是图G的一个好的画法，边 $e_1,e_2\in E\left(D\right)$， $p\notin V\left(D\right)$，如果 $e_1,e_2$ 都穿过p，即它们有一个公共点p，那么称e₁和e₂在D上相交于p，也可以将p称为D上的一个交叉点。图G在平面上的最优画法是指在图G的所有画法D中交叉点的数目是最少的画法，这个数目称为图G在画法D下的交叉数，简记为 $cr\left(D\right)$。

设A和B是E的两个互不相交的边子集，在画法D中， $c{r}_D\left(A,B\right)$ 表示由集合A中的边与集合B中的边产生的交叉个数，用 $c{r}_D\left(A\right)$ 表示由集合A中的边与边产生的交叉个数。

2.4. 图的好的画法

图的一个好的画法需要满足以下几点：

1) 没有边与自身交叉；

2) 一条边的两个顶点不能重叠，即一条边包含两个不同的顶点；

3) 相邻的两条边不相交，即具有公共顶点的两条边不产生交叉；

4) 若两条边产生交叉，则交叉点的数量最多是一个；

5) 两条边的相对位置不是相切；

6) 任意三条边不相交于同一个点。

除了特别指出，本文中所提及的所有画法均为好的画法。一个图可能会有多个好的画法，不同的图得到的画法可能相同 [4]。

2.5. 同构与自同构

对于两个图G和图H，如果在它们的顶点集合之间存在着一个保持邻接性的一一映射 $\varphi :V\left(G\right)\to V\left(H\right)$，使得对于任意 $u,v\in V\left(G\right)$，有 $\varphi \left(u\right),\varphi \left(v\right)\in V\left(H\right)$，同时满足 $\left(u,v\right)\in E\left(G\right)$ 当且仅当 $\left(\varphi \left(u\right),\varphi \left(v\right)\right)\in E\left(H\right)$，则称图G和图H是同构的，记作 $G\cong H$。

一个图G的自同构指的是图G与它自身的一个同构。

一个图的自同构可以反映出它的对称性。

2.6. 标定图与非标定图

如果一个图的顶点或边标出了文字，则称为标定图。否则，均未标记文字的图称为非标定图。

2.7. 度

在图G中，一个顶点v的度是指与顶点v相关联的G的边的数目，每个自环计数两次，顶点的度用d_G(v)表示。特别地，如果G是一个简单图，那么d_G(v)是G中顶点v的邻居的数目。度为零的顶点称为孤立点 [5]。

更多交叉数方面的知识见文 [1] 及其参考文献。

3. 三个顶点的所有标定简单图

定理1 对于有n个顶点的简单图G，其顶点集为 $V\left(G\right):=\left\{v_1,v_2,\cdots ,v_n\right\}$，则它的标定简单图有 $2^{\left(\begin{array}{c}n\\ 2\end{array}\right)}$ 个。

引理1 当n = 3时，其标定简单图有8个。

图1给出了三个顶点的所有标定简单图。

Figure 1. The eight labelled simple graphs on three vertices

图1. 三个顶点的8个标定简单图

4. 四个顶点的所有标定简单图

引理2 当n = 4时，其标定简单图的个数为64。

证明 假设G为四个顶点的简单图，则顶点集的数量v(G) = 4，边集的数量的最大值为6，此时G为完全图K4。由顶点的度之和以及度的相关性质可知，在这四个顶点中，任意两个顶点的度不能为0和3 (即0度顶点和3度顶点不能同时存在)。

根据边集的数目可分为以下7种情况进行讨论。

1) 边集的数目为0当且仅当G为空图。如图2所示。

Figure 2. The labelled simple graphs on four vertices

图2. 四个顶点的标定简单图

2) 当边集数目为1时，在此情况下标定简单图有 $C_4^2=6$ 个。如图3所示。

当边集数目为2时，所有顶点的度之和为4，那么度序列有以下三种子情况。

子情况1 度序列为0112。此时图G有12种标定简单图的情况。如图4所示。

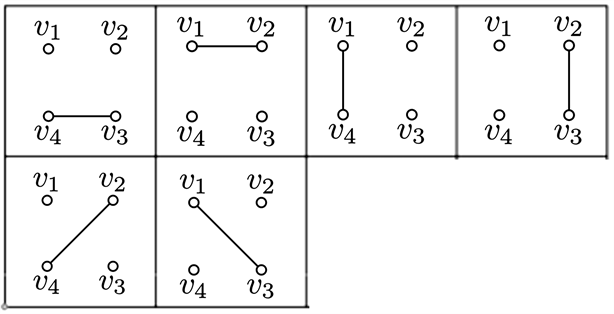
Figure 3. The labelled simple graphs on four vertices

图3. 四个顶点的标定简单图

Figure 4. The labelled simple graphs on four vertices

图4. 四个顶点的标定简单图

子情况2 度序列为0022。此时图G为圈或自环，不是简单图。

子情况3 度序列为1111。此时图G有3种为标定简单图的情况。如图5所示。

4) 当边集数目为3时，所有顶点的度之和为6，度序列有三种子情况。

子情况1 度序列为1122。此时图G有12种为标定简单图的情况。如图6所示。

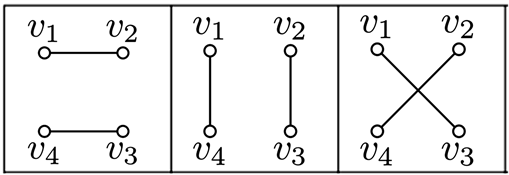
Figure 5. The labelled simple graphs on four vertices

图5. 四个顶点的标定简单图

Figure 6. The labelled simple graphs on four vertices

图6. 四个顶点的标定简单图

子情况2 度序列为0222。此时图G有4种为标定简单图的情况。如图7所示。

Figure 7. The labelled simple graphs on four vertices

图7. 四个顶点的标定简单图

子情况3 度序列为1113。此时图G有4种为标定简单图的情况。如图8所示。

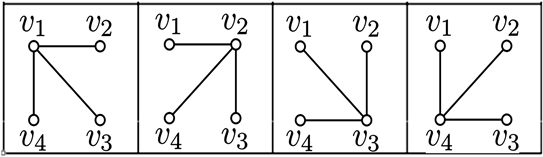
Figure 8. The labelled simple graphs on four vertices

图8. 四个顶点的标定简单图

5) 当边集数目为4时，所有顶点的度之和为8，并且每个点的度最少为1，因此度序列有三种子情况。

子情况1 度序列为1133。此时图G包含圈或自环，不是简单图。

子情况2 度序列为2222。此时图G有3种为标定简单图的情况。如图9所示。

Figure 9. The labelled simple graphs on four vertices

图9. 四个顶点的标定简单图

子情况3 度序列为1223。此时图G有12种为标定简单图的情况。如图10所示。

Figure 10. The labelled simple graphs on four vertices

图10. 四个顶点的标定简单图

6) 当边集数目为5时，标定简单图有 $C_4^2=6$ 个。如图11所示。

Figure 11. The labelled simple graphs on four vertices

图11. 四个顶点的标定简单图

7) 边集的数目为6当且仅当G为完全图K4。如图12所示。

Figure 12. The labelled simple graphs on four vertices

图12. 四个顶点的标定简单图

5. 四个顶点的所有非标定简单图

经过验证，四个顶点的非标定简单图共11个，如图13所示。

Figure 13. The unlabelled simple graphs on four vertices

图13. 四个顶点的非标定简单图

6. 结论

本文介绍了关于图论的基础知识，通过定理1的计算方法给定了四个顶点的标定简单图的数目，并构造出了全部画法。通过度序列的方法得到所有画法后，进一步与数学证明相结合，确定了四个顶点的标定简单图的数目的精确值为64个。最后给出了四个顶点的非标定简单图的数目为11个。