1. 引言
在无源定位与跟踪系统中，获取接收信号的多普勒频移及变化率信息对运动目标的状态估计和定位具有非常重要的意义[1] -[4] 。现有的无源定位技术，由于不能探测得到目标的中心频点，所以多普勒频移是无法直接测得的。基于多普勒测量方式的无源定位技术，一般只能通过采用多普勒频差测量技术而予以实现，这是因为多普勒频差能够通过对辐射频率差的测量而间接获得[5] [6] 。
事实上，通过简单的角度置换，我们即能获得在频移与相差之间的对应关系[7] ，且基于这种关系，多普勒频移就能通过简单的相差测量而被确定。但已有的基于相差的频移检测方法是建立在近似相差测向式的基础之上的[8] [9] ，本文进一步探讨分析了基于精确相差测向的多普勒频移计算方法。
2. 相差测向
2.1. 单基线近似测向式
如图1所示，设多通道相位干涉仪使用一个等效的单基线阵列对目标进行无源探测，为解相位模糊，其中等效的单基线阵列实际上是由多基线子阵组成的。如对应于每个径向距离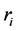
，鉴相单元所测得的相移是
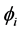，则有基于相移测量的距离公式：
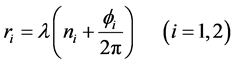(1)
式中：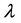
为波长；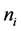
为波长整周数。
根据相移-距离关系(1)，在单基线两阵元径向距离间的程差可以由相差测量所确定，且即能得到在形式上与时差定位方程完全相类似的相差定位方程：
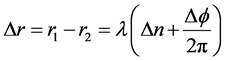(2)
式中：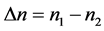
是程差所包含的波长整周数；
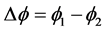为两阵元之间的相位差。
如假设来自同一辐射源的入射到两天线的信号近似为平面波，则由相位差-距离差的关系式(2)，按三角正弦定理即可近似得到现有的相位干涉测向公式：
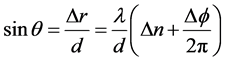(3)
即有：
(4)
式中：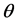
为信号的到达角；
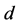为阵元间的距离。
2.2. 一维双基精确解
对于图2所示的几何模型，由余弦定理可列出如下两个几何方程：
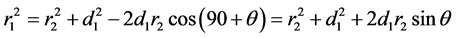(5)
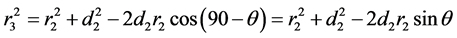(6)
因有：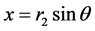
，故几何辅助方程可改写为：
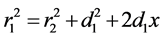(7)
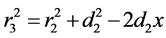(8)
设：
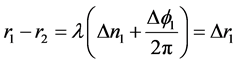
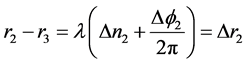
式中：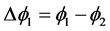
；
。
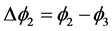将上面两式代入几何辅助式(7)和(8)，且为表达简便，直接用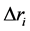
表示相差测量项。在移项整理后有
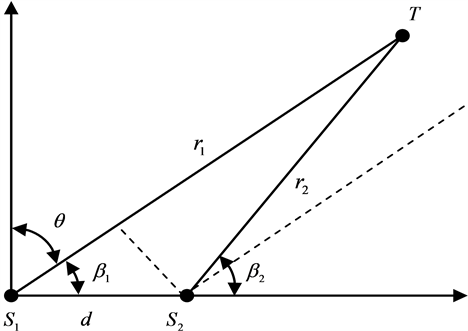
Figure 1. Single baseline direction finding array based on phase interference measuring
图1. 等效单基线相位干涉测向阵列
Figure 2. A one-dimensional double-base line direction finding array based on phase interference measuring
图2. 一维双基线相位干涉测向阵列
如下的二元一次线性方程组：
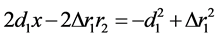(9)
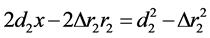(10)
从中可以直接解出：
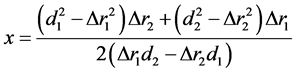(11)
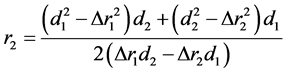(12)
由求得的目标位置参数，即能得到目标的到达角：
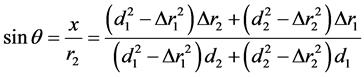(13)
注意，符号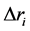
实际上表示的是相位测量项：
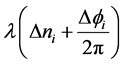，即到达角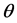
是由相差测量得到的。
3. 频移的相差检测
假设在机载平台上安置一维双基阵，在直线阵列的各个阵元处所接收到的多普勒频移是：
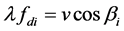(14)
式中：
为多普勒频移；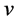
为机载平台的移动速度；
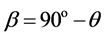为前置角。
因有：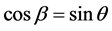
，利用基于相差检测的近似测向式，即能得到基于相差测量的多普勒频移近似计算公式：
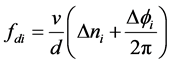(15)
如将测向严格解代入，则得到：
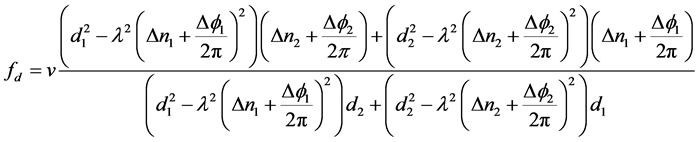(16)
若相邻两基线相等，则有：
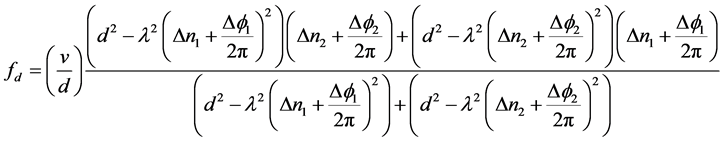(17)
图3给出了频移严格相差检测解的相对计算误差。模拟计算表明，严格解的计算准确度有了很大的提高。
4. 精度分析
根据误差估计理论，基于相差测量的频移计算式的测量误差是：
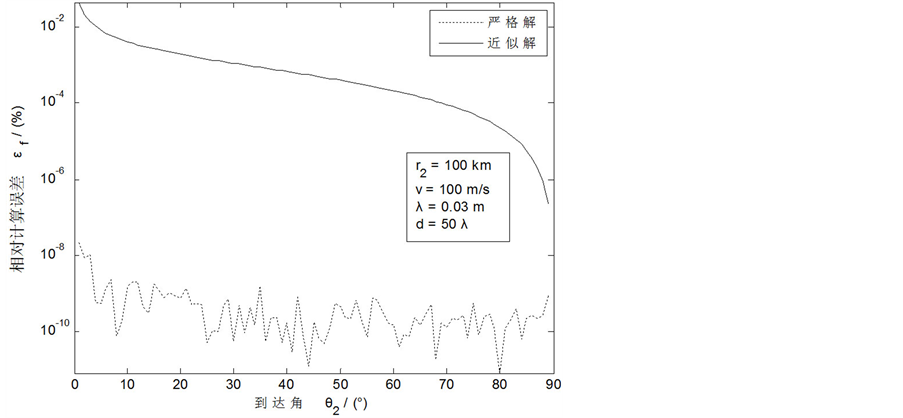
Figure 3. Comparing between rigorous solution and approximate solution
图3. 严格解与近似解的比较
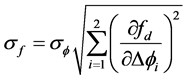(18)
式中：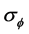
为相位差测量误差的均方根值。
设：
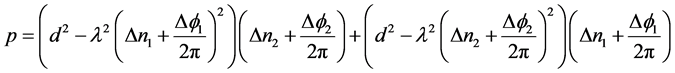
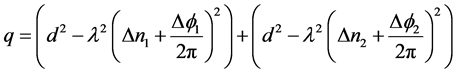
通过对相差求微分所得到的各个误差分量是：
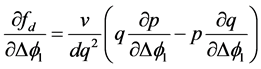(19)
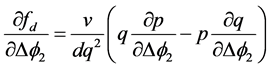(20)
其中：
图4给出了在不同基线长度时的测频误差，显然，增长基线和减小相差测量误差都将有利于降低测频误差。当基线长度为几十个波长时，在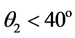
的范围内，多普勒频移的测量误差可小于5赫兹。
5. 结语
相移与频移函数关系的一个较为重要的应用就是有效解决了对多普勒频移的检测问题[7] ，即机载多普勒频移可以通过相位干涉测量而获得。
由于包含有被测目标的信号波长，尽管基于精确相差测向所得到的多普勒频移计算式是更为准确的，但对无源定位而言可能还缺乏实际的使用价值。相比之下，基于近似相差测向所导出的多普勒频移计算式则是与信号波长无关的。