非理想Buck变换器分数阶建模及参数辨识研究

Parameter Identification of Buck Converter Based on the Non-Ideal Fractional Model

摘要: 基于实际电容和电感本质上是分数阶的事实，针对以往开关变换器建模过程中一些理想化假设会引起较大误差的问题，建立了电感电流连续模式下Buck变换器的非理想状态分数阶模型及状态平均模型，提出了一种用于分数阶模型阶次辨识的改进随机数辨识方法，通过仿真验证了运行非理想状态下Buck变换器的分数阶仿真模型的合理性和可行性，并对Buck变换器分数阶阶次进行辨识，与一般传统的算法对比，结果表明改进的方法具有更高的准确性。

Abstract: Based on the fact that the capacitor and the inductor are fractional in nature, and some ideal as-sumptions could bring errors during the modeling of the switching converters, the fractional mathematical and the fractional state averaged model of the not ideal buck converter in continu-ous mode operation are built and analyzed, a parameter identification method that can be applied in fractional model is proposed. Finally, to verify the theoretical analysis the simulation model of the buck converter in continuous conduction mode operation is established by using the software of Matlab/Simulink, the validated of the new identified method is validated by compared with traditional methods.

1. 引言

开关变换电源的建模分析是研究开关电源的基础，对开关电源的分析与设计具有重要意义，决定着开关变换器控制器设计性能的高低，是当前电力电子技术领域的研究方向之一 [1] [2] [3] 。开关变换器传统建模主要基于整数阶模型，但随着人们研究的深入发现，电路中的电容和电感在本质是分数阶的，建立相应的分数阶模型更能准确的描述实际电容和电感的电特性 [4] [5] 。以往建模过程中，为简化模型往往忽略电路中的寄生参数，这样得到的理想化模型在实际应用中存在误差，有一定局限性 [6] [7] [8] [9] 。针对这一问题，本文采用基于分数阶的状态平均法建立了Buck变换器在考虑各种非理想因素条件下的数学模型，采用改进的随机数直接搜索法对分数阶变换器进行阶次的辨识研究，通过仿真实验平台对Buck变换器仿真，验证了分数阶变换器建模理论的正确性和随机数辨识法的可行性。

2. 理论建模

2.1. Buck的工作原理和状态平均模型

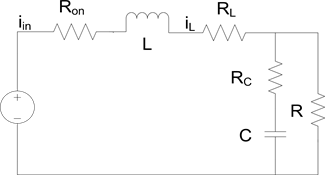
Buck变换器又称降压变换器，它是一种对输入输出电压进行降压变换的直流斩波器，即输出电压低于输入电压。Buck电路的基本拓扑电路如图1所示， $Q$ 为周期开关脉冲信号，其开关周期为 $T$ 。设Buck变换器输入电压为 $V_{in}$ ，电感电流为 $i_L\left(t\right)$ ，输出电压为 $V_0\left(t\right)$ 。Buck变换器工作在电感电流连续模式下，当周期性开关脉冲信号为高电平时，功率开关 $Q$ 导通，电感电流大于负载电流时，电容处于充电状态，二极管承受反向电压而截止，电感输入端电压值为直流输入电压与开关导通压降只差，称为Buck工作模态1；当功率开关 $Q$ 截止、二极管导通时，电感 $L$ 为了保持其电流 $i_L\left(t\right)$ 不变，负载电压 $V_0\left(t\right)$ 仍是上正下负，电感电流小于负载电流时，电容处于放电状态，通过二极管续流，电感输入电压值为二极管正向导通电压，称为Buck工作模态2。

2.2. 非理想状态下Buck电路模型

本文讨论的非理想条件是指考虑开关管导通电阻 $R_{on}$ 、二极管导通正向压降 $V_d$ 、电感等效串联电阻 $R_L$ 、电容等效串联电阻 $R_C$ 。在非理想条件下，对Buck变换器的建模作如下定义：1) 二极管导通状态由正向压降 $V_d$ 来代替，关断电阻近似为无穷大；2) 滤波电容足够大，流过电流恒定。可见，非理想Buck变换器处于2种不同工作过程，如图2所示。

3. Buck变换器的分数阶状态平均模型的建立与分析

根据分数阶电感和分数阶电容的数学模型以及上述的2种工作模态，可得运行于电感电流连续模式

Figure 1. Schematic diagram of Buck converter

图1. Buck变换器原理结构图

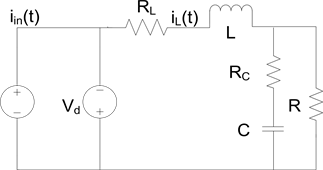(a) (b)

Figure 2. The working process of non-ideal Buck converter. (a) topology diagram (Q turn-on and D turn-off); (b) topology diagram(Q turn-off and D turn-on)

图2. 非理想Buck变换器工作过程. (a) Q导通，D关断时的拓扑结构图；(b) Q关断，D导通时的拓扑结构图

下Buck变换器的数学模型如下：

工作模态1： $\{\begin{array}{l}\frac{{\text{d}}^{\alpha }{i}_L}{\text{d}{t}^{\alpha }}=-\frac{R_{on}+R_L}{L}{i}_L-\frac{v_0}{L}+\frac{v_{in}}{L}\\ \frac{{\text{d}}^{\beta }{v}_0}{\text{d}{t}^{\beta }}=\frac{R}{C\left(R+R_C\right)}\left[1-\frac{C{R}_C(R_{on}+R_L)}{L}\right]i_L-\frac{C{R}_{C}R+L}{CL\left(R+R_C\right)}{v}_0+\frac{R_{C}R}{L\left(R+R_C\right)}{v}_{in}\end{array}$ (1)

工作模态2： $\{\begin{array}{l}\frac{{\text{d}}^{\alpha }{i}_L}{\text{d}{t}^{\alpha }}=-\frac{R_L}{L}{i}_L-\frac{v_0}{L}+\frac{v_d}{L}\\ \frac{{\text{d}}^{\beta }{v}_0}{\text{d}{t}^{\beta }}=\frac{R}{C\left(R+R_C\right)}\left[1-\frac{C{R}_C{R}_L}{L}\right]i_L-\frac{C{R}_{C}R+L}{CL\left(R+R_C\right)}{v}_0-\frac{R_{C}R}{L\left(R+R_C\right)}{v}_d\end{array}$ (2)

采用状态平均法进行电路状态平均变换时，需满足三点假设：1) 低频假设，交流小信号的频率应远小于开关频率；2) 小纹波假设，变换器的转折频率远小于开关频率；3) 小信号假设，电路中各变量的交流分量幅值远小于相应的直流分量。在本文研究的Buck变换器中，开关频率一般在 ${10}^{-5}$ 的级别，直流分量幅值远大于交流分量，容易满足状态平均法的假设。基于上式(1)、(2)以及状态平均建模方法，并根据分数阶微积分的性质，可直接得到工作电感电流连续状态下非理想Buck变换器的分数阶状态平均模型为：

$\{\begin{array}{l}\frac{{\text{d}}^{\alpha }\langle i_L\rangle }{\text{d}{t}^{\alpha }}=-\frac{d{R}_{on}+R_L}{L}\langle i_L\rangle -\frac{v_0}{L}+\frac{d\langle v_{in}\rangle }{L}-\frac{d^{\prime }{v}_d}{L}\\ \frac{{\text{d}}^{\beta }\langle v_0\rangle }{\text{d}{t}^{\beta }}=\frac{R}{R+R_C}\left[\frac{1}{C}-\frac{R{R}_C}{L}-\frac{R_{on}{R}_C}{L}d\right]\langle i_L\rangle -\frac{C{R}_{C}R+L}{CL\left(R+R_C\right)}\langle v_0\rangle +\frac{R_{C}R}{L\left(R+R_C\right)}d\langle v_{in}\rangle -\frac{R_{C}R}{L\left(R+R_C\right)}{d}^{\prime }{V}_d\end{array}$ (3)

4. 基于改进的随机数搜索辨识法

电力电子电路在工作中具有时变、非线性等特点，无法直接应用一些经典的、精确的电路分析方法。针对电力电子电路的这些性质，本文采用一种改进的随机数搜索法进行电力电子分数阶参数模型的辨识。针对Buck电路分数阶小信号模型，在模型结构已知的条件下计算步骤如下：

1) 确定要搜索的分数阶系统的微分项系数和阶次

2) 产生随即搜索向量

3) 选择评价函数，如式(4)所示

$\Phi ={\displaystyle \int \left(y_0\left(t\right)-\tilde{y}\left(t\right)\right)\text{d}t}$ (4)

其中 $y_0\left(t\right)$ 表示在阶跃激励下测得实际对象输出， $\tilde{y}\left(t\right)$ 表示阶跃激励下模型的输出。

4) 选择适当的初值与范围

选择一组随机数或一组整定参数作为初值 $x_{\left(i\right)}^0$ ，并确定初始半径 $r_{\left(i\right)}^1$ 为初值的若干倍，即：

$r_{\left(i\right)}^1=C{x}_{\left(i\right)}^0$ (5)

其中， $r$ 为半径，其通式是 $r_{\left(i\right)}^j$ ， $i=1,2,\cdots ,n$ 。 $n$ 表示寻优参数的个数； $j$ 为迭代次数， $j=1,2,\cdots ,100$ 。

5) 迭代计算

按照下式估算模型的参数：

$x_k^j\left(i\right)=x_k^{j-1}\left(i\right)+v_{ki}{r}_k^j\left(i\right)$ (6)

6) 选择收缩系数 $\psi$

为了加快收敛速度，提高搜索效率，所以将在每一次迭代计算之后缩小搜索半径 $r_i^j$ ，即：

$r_i^j=\psi r_i^{j-1}$ (7)

7) 修正搜索范围 $r_i^j$

$X_0$ 为要辨识参数的初值 $x^{\left(0\right)}\left(i\right)$ 。首先设定搜索半径允许的最大比例 $\eta$ 。(一般大于0，可设为 $\eta =1.5$ )。若某一变量 $x_j$ 在搜索后改变比率大于 $\eta$ ，说明该变量的目前位置距离最佳位置较远，则不改变其搜索半径。即搜索半径的调整通过下式表示：

$r_i^0=C{X}_0$ (8)

$r_i^j=C{X}_{j-1}\times v_j,j>0$ (9)

其中 $v_j$ 取值为：当 $j=0,1$ 时， $v_j=1$ ；当 $j>1$ ，若 $1/\eta <\left|X_{j-1}/X_{j-2}\right|<\eta$ 则 $v_j={\psi }_j\times v_{j-1}$ ；否则 $v_j=1$ 。

8) 迭代搜索

重复步骤(5)，(6)与(7)进行下一次迭代计算。一般情况下迭代100次，计算结果己经可以收敛了，然后输出辨识结果。

5. 仿真及结果分析

5.1. 状态空间平均法的仿真

为了进一步验证上述非理想Buck分数阶建模与理论分析的正确性，根据Matlab/Simulimk软件以及薛定宇等人 [10] 提出的改进Oustaloup滤波器分数阶微分算法，分别建立电感电流连续模式下Buck变换器分数阶模型和分数阶平均状态的Simulimk仿真模型，Oustaloup滤波器的分数阶微积分算法三个主要参数 [11] ：拟合下限频率 ${\omega }_b$ 、拟合上限频率 ${\omega }_h$ 、滤波器阶数 $2N+1$ 。在对实际分数阶系统进行仿真时，需根据系统的频率范围选择拟合频率段 $\left({\omega }_b,{\omega }_h\right)$ 和 $N$ 值，取 ${\omega }_b{\omega }_h=1$ 。选择电路参数当 $\alpha ,\beta =0.9$ 时， $R=10\Omega$ ， $v_{in}=20\text{V}$ ， $L=1\text{mH}$ ， $C=47\mu \text{F}$ ， $d=0.5$ ， $f=25\text{kHz}$ ，且认为 $\langle d\rangle =0.5$ ， $\langle v_{in}\rangle =20\text{V}$ 。此时电流 $0.5\ast \Delta i_L\prec I_L$ 电路工作在电感电流连续的状态下。

图3中的Fractional Int s^(a)模块式分数阶积分单元，由于开关频率为 $f=25\text{kHz}$ ，即相应的 $\omega =2\text{π}f\approx 1.57\times {10}^5\text{rad}/\text{s}$ ，考虑到存在高于开关频率的高频谐波在，选择 ${\omega }_h>1.57\times {10}^5\text{rad}/\text{s}$ ，因此选 ${\omega }_h=5\times {10}^5\text{rad}/\text{s}$ ， ${\omega }_b=2\times {10}^{-6}\text{rad}/\text{s}$ ， $N=8$ 。对采用分数阶和状态平均法得到的非理想Buck变换器数学模型公式(1)、(2)和(3)，应用Matlab/Simulink建立仿真模型，如图3(a)图3(b)所示。两种模型的仿真结果如图4(a)图4(b)所示。

Figure 3. The simulation model of the Buck converter under non-ideal state. (a) fractional order model of Buck converter; (b) fractional order state average model of converter

图3. 非理想状态下Buck变换器电路的仿真模型。(a) Buck变换器分数阶模型；(b) Buck变换器分数阶状态平均模型

Figure 4. Simulation waveform of Buck converter circuit. (a) integer order simulation waveform of Buck converter; (b) fractional order simulation waveform of Buck converter

图4. Buck变换器电路的仿真波形。(a) Buck变换器整数阶仿真波形；(b) Buck变换器分数阶仿真波形

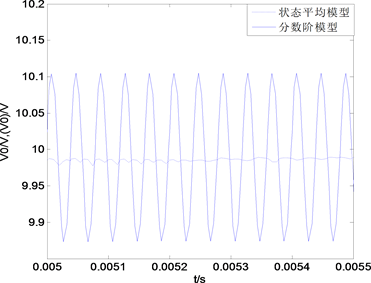
当系统运行达到稳态时，两种模型下的电感电流 $i_L$ 和输出电压 $v_0$ 波形分别如图5(a)(b)所示。根据图5(a)知Buck变换器运行在电感电流连续的模式下， $i_{L\max }=1.332\text{A}$ ， $\langle i_L\rangle =0.971$ ；根据图5(b)可测量， $v_{0\max }=10.11\text{V}$ ， $\langle v_0\rangle =9.98\text{V}$ 。由于电路交流分量远小于直流分量，因此 $V_0\approx \text{9}\text{.98}\text{V}$ ， $I_L\approx 0.971\text{A}$ 。同时根据公式分别计算出 $V_0=9.797\text{V}$ ， $I_L=0.977\text{A}$ 。由此可见，本文采用数值仿真的结果与理论计算结果基本一致，误差很小。证明在电感电流连续状态下，非理想Buck变换器的分数阶模型和理论是正确的。

5.2. Buck电路分数阶参数辨识算法及结果分析

在前面已对Buck电路非理想分数阶模型进行了理论分析与仿真实验，在此基础上对分数阶系统参数辨识进行验证，Buck变换器电路分数阶参数辨识的基本思路为：首先根据Buck电路小信号模型建立电路输出阻抗传递函数模型，其次，获取电路的单位阶跃响应的信号，通过仿真之后将输出小信号电流和输出小信号电压数据采集到Matlab的Workspace中，然后进行参数辨识可得到分数阶参数，仿真实验中器件的参数同上。同时与采用最小二乘法的辨识方法 [12] 进行对比，仿真结果如图6、图7所示。图中a表示电路的分数阶阶数，k表示分数阶模型的增益系数。

从图7中可以看到在本文预设的分数阶参数为 $\alpha ,\beta =0.9$ 的情况下，运用两种方法对Buck分数阶参数进行辨识，在进化代数相同情况下，本文改进的方法得到结果为 $\alpha =0.9$ ， $k=1$ ；传统的最小二乘法得到结果为 $\alpha =0.8774$ ， $k=0.9829$ ，由此可见在近似的单分数阶参数辨识中，本文提出的分数阶参数辨识方法进行能够对电感电流连续状态下，Buck变换器分数阶阶数进行辨识。

6. 结束语

本文基于分数阶微积分理论，对非理想状态下的Buck变换器进行建模，分析了分数阶模型和分数阶平均状态模型与传统整数阶电路的区别，通过分析表明，Buck变换器在电感电流连续的状态下，其稳态直流分量与电容和电感的分数阶阶数无关，但在交流小信号分析中，纹波电压和纹波电流均与电感和电容的分数阶阶数有关，因此在考虑电感和电容是分数阶的本质前提下，建立电力电子变换器分数阶工作模型，显得尤为重要。最后设计了一种改进的随机数搜索法对分数阶系统阶数辨识进行了研究，结果表明该方法在一定程度上能够解决分数阶非线性算子的辨识问题。

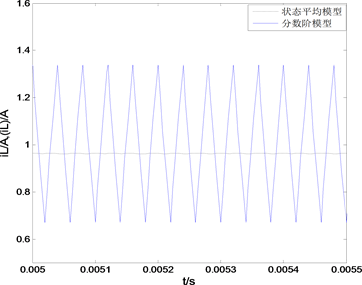(a) (b)

Figure 5. Circuit simulation waveform of Buck fractional order. (a) current simulation waveform; (b) voltage simulation waveform

图5. Buck分数阶电路仿真波形。(a) 电流仿真波形；(b) 电压仿真波形

Figure 6. Improved random number identification results

图6. 改进的随机数辨识结果

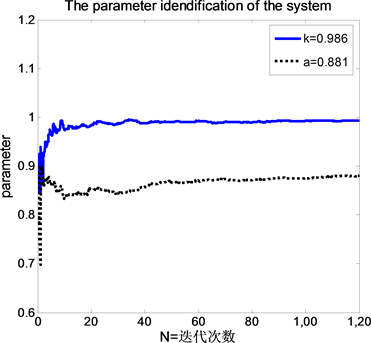
Figure 7. Least squares identification results

图7. 最小二乘辨识结果

本文侧重于理论验证，下一步将通过实验平台对电力电子电路的分数阶特性进行分析，同时在系统结构不确定的情况下进行电路的分数阶模型参数辨识，还有待进一步的深入研究。

致 谢

本文的撰写是在我院电力系统教研室李孝全副教授指导下完成的，在此表示诚挚的谢意！