忆阻器新型非线性窗口函数的伏安特性研究

Research on the Voltammetric Characteristics of a New NonlinearWindow Function of Memristor

摘要: 在本文中，基于我们提出的新型窗口函数的忆阻器模型为研究对象，调节忆阻器模型中的相关参数，研究其伏安特性曲线的变化规律。由数值模拟结果表明，首先，现有窗口函数存在一些不足之处：容易发生终态问题，调控的灵活性不高；其次，选取描述窗口函数特性的内部参数为控制变量，数值模拟其伏安特性的演化规律；接着，引入外部的激励电压，并调节信号的频率。研究结果发现，我们提出的新型窗口函数不仅能有效的解决现有窗口函数的不足，而且，对外部不同频率的刺激信号也具有较好的辨识能力。上述研究结果将帮助我们更进一步的了解忆阻器的非线性特性，为未来深入理解其调控机理和研发具有特定功能的电子器件都有一定的理论意义和指导作用。

Abstract: In this paper, based on the memristor model with our new window function, the regulation of voltammetric characteristics was studied by adjusting the related parameters of the memristor model. Simulation results show that, firstly, the existing window functions have some shortcomings: It is easy to appear the terminal state problem, and the flexibility of regulation needs to be improved. Secondly, to simulate the evolution of the voltammetric characteristics, the internal parameters describing the characteristics of the window function is selected as the control variables. Furthermore, to study the dynamical behavior of memristor the external excitation signal is introduced and the frequency of the external excitation signal is adjusted. The results show that our new window function not only can effectively solve the shortcomings of the existing window function, but also has a good ability to identify the stimulus signals with different frequencies. These results will help us to further study the nonlinear characteristics of memristor, and have theoretical significance and guidance for further understanding of the mechanism of memristor and the development of electronic devices with specific functions.

1. 引言

忆阻器作为一种具有记忆功能的非线性电阻，自1971年由蔡少棠基于电荷、电流、电压和磁通之间的关系以及电路完备性理论提出以来，人们从理论和实验两个方面对其进行了不懈的探索和研究 [1] 。直到2008年，惠普实验室Strukov等人首次在物理上实现了基于TiO_x的忆阻器，人们发现该型忆阻器理想的理论模型的伏安曲线具有典型的“8”字型迟滞回线，且随着外部信号频率的增加该曲线逐渐趋于一条直线，表明理想HP模型具有对阻值的记忆能力 [2] ，至此，对忆阻器的研究才开始受到人们的广泛关注。

人们通过研究发现忆阻器有许多独特的动力学特性，Makoto等人发现忆阻器的非线性特性可以产生混沌现象，是构造混沌和超混沌系统的理想元件 [3] [4] [5] [6] 。惠普忆阻器具有记忆和布尔逻辑运算功能，这标志着存储电路和逻辑运算可以合二为一，从而创建起全新的计算机系统 [7] [8] [9] 。忆阻器具有与生物神经突触功能包括记忆与遗忘、经验学习等相似的特性，是目前已知的功能最接近神经元突触的器件 [10] [11] [12] [13] 。因此忆阻器不仅可用于研究混沌现象，而且可用于超大型集成网络和非易失随机访问存储器 [3] [4] [5] [6] 。除此之外，忆阻器在人工神经网络，机器学习和人工智能计算机方面也有着极为重要的作用 [13] [14] [15] [16] 。

由于实物忆阻器处于纳米尺度范畴，其掺杂区界面移动的动力学行为是高度非线性的，因此，为深入了解忆阻器忆阻的变化规律，为将来能将其视作突触应用于神经元网络之中，有必要从理论上对忆阻器窗口函数的伏安特性及其调控机理进行深入研究。本文我们首先介绍几种忆阻器的窗口函数，分析其不足和需要改进之处。第二部分分析了这些窗口函数的伏安特性，以及不同控制参数作用下的行为和演化规律。第三部分对模拟结果进行了分析与讨论，最后对本文进行了总结。

2. 忆阻器模型描述

忆阻器是连接电荷与磁通量的一种无源电路元件，忆阻M与电阻的量纲相同。其定义如下 [17] ：

$\text{d}\phi =M\text{d}q$ (1)

2008年惠普实验室提出了一个基于TiO₂的双极忆阻器：在两个Pt电极中间加上有高阻特性的纯净TiO₂和低阻特性的掺杂TiO_2−x组成的TiO₂薄膜，此时忆阻器总电阻为掺杂区域电阻加上非掺杂区域电阻之和的可变电阻 [2] ，忆阻值M(ω)可以表示为：

$M\left(\omega \right)=\frac{\omega }{D}{M}_{on}+\left(1-\frac{\omega }{D}\right)M_{off}$ (2)

TiO_2−x缺少氧原子，携带一定的电荷。在两个Pt电极之间的电场的作用下，带电杂质TiO_2−x开始发生偏移，TiO₂和TiO_2−x的分界面随之迁移。分界面的移动速度取决于电流强度。用状态变量ω表示完全

掺杂区的厚度，则 $\frac{\text{d}\omega }{\text{d}t}=g\frac{{\mu }_v{M}_{on}}{D}i\left(t\right)$ 。该式由惠普实验室通过大量实验数据给出，g表示忆阻器的极性 [18]

[19] 。D为忆阻器薄膜的宽度，M_on和M_off分别为完全掺杂以及完全无掺杂时忆阻器阻值。

对于纳米尺度范畴的电子器件来说，一个微小的电场就会对器件产生巨大的影响，当分界面的迁移接近两极接触面的任意一个时，分界面的迁移速率在偏置极性的同极相斥作用下被抑制。由于TiO₂和TiO_2−x的分界面在大部分区域内保持恒定的迁移速度，仅在接近两极的小部分区域受到同极相斥作用的影响，所以引入适当窗口函数可以描述这种非线性特性 [18] [19] 。因此完全掺杂区的厚度ω随时间变化满足 [20] ：

$\frac{\text{d}\omega }{\text{d}t}=\frac{{\mu }_V{M}_{on}}{D}i\left(t\right)g\left(x\right)$ (3)

$x=\frac{\omega }{D}$ (4)

$\frac{\text{d}x}{\text{d}t}=\frac{{\mu }_V{M}_{on}}{D^2}i\left(t\right)g\left(x\right)$ (5)

x用来描述掺杂区与忆阻器宽度的比值， ${\mu }_V$ 为离子迁移速率。i(t)表示通过忆阻器的电流，引入激励电压 $V\left(t\right)=M\left(q\left(t\right)\right)i\left(t\right)$ 。 $g\left(x\right)$ 为边界迁移的窗口函数，描述TiO₂和TiO_2−x分界面迁移的非线性掺杂动力学行为，当 $g\left(x\right)=1$ 时，掺杂边界为线性迁移。

由于忆阻器的设计要求较高，直接利用实物忆阻器来研究较为困难，因此，目前通常人们将忆阻器引入到理想电路中构建理论模型，然后利用数值仿真来分析其特性是较为广泛的一种研究方法 [2] [19] 。

3. 结果与讨论

3.1. 非线性窗口函数

为了研究忆阻器的非线性特性，科研工作者们提出了许多描述TiO₂和TiO_2−x分界面迁移的非线性掺杂动力学行为的窗口函数模型，借助于这些模型，人们从理论上对忆阻器开展了相关研究，了解了相应的伏安特性。下面首先就这些窗口函数进行一些分析和讨论。

最早在2008年Strukov等人就提出了一个窗口函数 [3] ：

$g\left(x\right)=x-x^2$ (6)

该窗口函数没有内部调整参数，缺乏灵活性，不能满足条件 $0\le g_{\max }\left(x\right)\le 1$ ，也无法提供掺杂线性与非线性迁移之间的联系。随后，2009年Joglekar等人提出了描述非线性掺杂剂迁移特性的窗口函数 [20] ：

$g\left(x\right)=1-{\left(2x-1\right)}^{2p}$ (7)

其中引入了一个取正整数的内置控制参量p。该窗口函数虽然引入了一个内部控制变量，使得模型有一定的调控灵活性，但在掺杂剂耗尽( $\omega \to 0$ )或者饱和( $\omega \to D$ )时， $g\left(x\right)\equiv 0$ 不再变化，这使得模型出现了“终态问题”。接着，Biolek等将电流与掺杂迁移联系起来提出如下函数 [21] ：

$\begin{array}{l}g\left(x\right)=1-{\left[x-\mathrm{sgn}\left(-i\right)\right]}^{2p}\\ \{\begin{array}{l}\mathrm{sgn}\left(i\right)=1\begin{array}{ccc}& & i\ge 0\end{array}\\ \mathrm{sgn}\left(i\right)=0\begin{array}{ccc}& & i<0\end{array}\end{array}\end{array}$ (8)

该窗口函数将忆阻器电流 $i\left(t\right)$ 引入到窗口函数中，虽然较好地解决了“终态问题”，但是该窗口函数不满足非线性连续变化的条件。Prodromakis等人在Strukov窗口函数的基础上提出了包含两个控制参量的窗口函数 [22] ：

$g\left(x\right)=q\times \left(1-{\left[{\left(x-0.5\right)}^2+0.75\right]}^p\right)$ (9)

其中引入q、p两个内部参数能使得该模型具有很好的灵活性，但没有解决终态问题。

由上可见，这些窗口函数都不能很好地解决终态问题和调控的灵活性，因此我们最近提出了一种基于正弦函数的窗口函数模型，较好的弥补了这两个方面的缺陷，模型方程如下：

$g\left(x\right)=q\times {\sin }^{\frac{1}{p}}\left(\text{π}x\right)$ (10)

该函数解决了终态问题，又因为引入了q、p两个内部参数具有良好的灵活性。本文中，我们以此新的窗口函数为研究对象，分别选取内置参数q、p，以及掺杂区与忆阻器宽度的比值x作为控制参量，考察窗口函数的伏安特性以及其动力学行为。其他参数取值为： $D=1\times {10}^{-8}$ ， ${\mu }_V=1\times {10}^{-14}$ ，时间步长取dt = 0.0002。利用龙格库塔法对上述方程(1-5)式及(10)式进行数值积分，记录忆阻器两端电压 $V\left(t\right)$ 和通过忆阻器的电流 $i\left(t\right)$ ，以及忆阻值随时间的演化结果，进行相关分析。

3.2. 伏安特性曲线

首先，我们选取参数 $\alpha =M_{off}/M_{on}$ 为控制变量，引入激励电压 $V\left(t\right)=1.2\sin \left(2\text{π}ft\right)$ ，考察系统伏安特性随着相应参数变化的行为和规律。其他相关参数分别固定为x = 0.25，f = 0.05 Hz，M_on = 1 Ω。调节完全无掺杂以及完全掺杂时忆阻器阻值之比α的值，选取几个有代表性的α = 6、10、20、40、60、80、100等，记录系统在不同的完全无掺杂以及完全掺杂时阻值的比值α下伏安特性曲线如图2(a-b)所示。从图1中可以看出，当α的值较小时，曲线由“8”字型退化为一条斜直线，如图1(a)中α = 6所示。而随着α的增大，均呈现出不同的迟滞回线特性。

其次，设置α = 160，f = 0.05，在 $x\in \left(0,1\right)$ 范围内调节x的大小，选取几个有代表性的x = 0.1、0.2、0.4、0.6、0.8、0.9，记录系统在不同的掺杂区和总宽度之比x下的伏安特性曲线如图2(a, b)所示。从图2中可以看出，x取值不宜过大，否则曲线会退化为斜直线，如图2(b)中x = 0.9所示。只有当x取值适当时，忆阻器具有灵活多变的伏安特性和复杂多样的动力学行为。

再次，我们固定设置α = 160，x = 0.25，调节外接电压频率f的值，选取几个有代表性的f = 0.1、0.2、0.3、0.4、0.5、0.6、0.8、1，记录系统在不同的频率下的伏安特性曲线如图3(a, b)所示。从图3中可以看出，当f的值较小时，伏安曲线会退化成一条斜直线，如图3(a)中f = 0.1所示。而f取其他值时均呈现出较好的伏安特性。另一方面，随频率f值的增大，曲线逐渐趋向于一条直线。

最后，设置 $D=1\times {10}^{-8}$ ， ${\mu }_v=1\times {10}^{-14}$ ，调节内置参数p = 0.5，q = 3，分别考察当α，x和f三参数

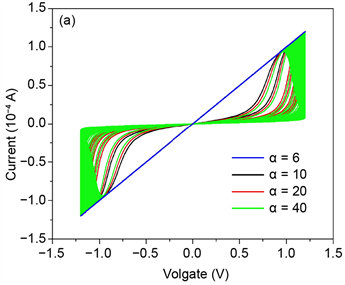
Figure 1. Current-voltage curves with different α values.

图1. 不同的α下忆阻器伏安特性曲线

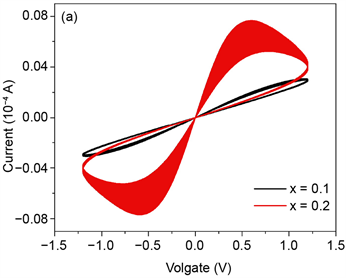
Figure 2. Current-voltage curves with different x values.

图2. 不同的x下忆阻器伏安特性曲线

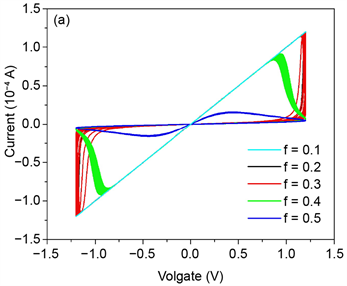
Figure 3. Current-voltage curves with different f values.

图3. 不同的频率f下忆阻器伏安特性曲线

中固定两个参数不变，改变第三个的值，记录相应的伏安特性曲线。模拟结果如图4所示。(i)固定x = 0.25，f = 0.05 Hz，选取α = 3、10、30、60、160等值，(ii)固定α = 160，f = 0.05 Hz，x = 0.1、0.5、0.6、0.8；(iii)固定x = 0.25，α = 160，f = 0.1、0.2、0.4、0.8。所得结果如图4(a)-(c)所示。若改变内置参数p，q重复上述内容，均能得到类似结果。我们发现其伏安曲线出现“8”字型的迟滞回线，且随着频率的增加其迟滞曲线逐渐趋于一条直线，上述模拟结果表明，(10)式对应的窗口函数能较好地与Strukov等人在物理上实现的电子元件的非线性特性相吻合，且引入的内置参数p，q使得窗口函数的伏安特性具有较好的灵活可控性。这些变化规律与特征，均与HP忆阻器的非线性特性在定性上相吻合。

4. 总结

综上所述，本文中我们采用基于正弦函数而引入新的窗口函数，调节相应的控制参量，研究了模型的伏安特性曲线的演化规律。通过数值模拟发现，该窗口函数有效地改善了现有函数的两点不足之处；引入一定频率的外部刺激信号，并通过改变相应的控制参数α、f、x和窗口函数的内置参数p，q，发现

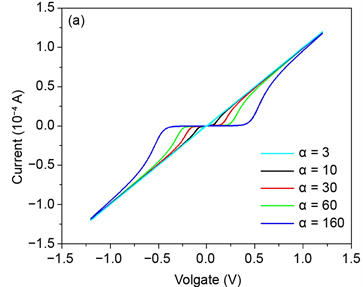
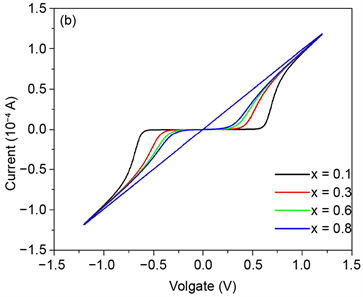
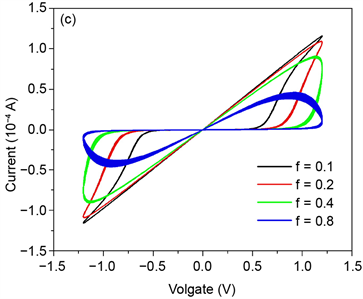
Figure 4. Current-voltage curves with different parameters values. (a) x = 0.25, f = 0.05 Hz, α = 3, 10, 30, 60, 160. Current-voltage curves with different α values. (b) α = 160, f = 0.05 Hz, x = 0.1, 0.5, 0.6, 0.8. Current-voltage curves with different x values. (c) x = 0.25, α = 160, f = 0.1, 0.2, 0.4, 0.8. Current-voltage curves with different f values

图4. 忆阻器伏安特性曲线在不同参数下变化示意图。(a) x = 0.25, f = 0.05 Hz, α = 3, 10, 30, 60, 160。不同α下忆阻器伏安特性曲线。(b) α = 160, f = 0.05 Hz, x = 0.1, 0.5, 0.6, 0.8。不同x下忆阻器伏安特性曲线。(c) x = 0.25, α = 160, f = 0.1, 0.2, 0.4, 0.8。不同频率f下忆阻器伏安特性曲线

窗口函数的伏安特性具有较好的灵活可控性。由于忆阻器具有良好的记忆能力和逻辑运算功能，将来有望作为突触连接应用于人工神经网络、智能计算、人工突触等诸多领域 [23] 。因此，我们的研究结果将会帮助我们深入了解忆阻器的非线性特性，为日后进一步探究理解忆阻器的调控机理和研发具有特定功能的电子器件都有一定的理论意义和指导作用。

致谢

感谢安徽省自然科学基金项目(No: 1508085MA15)、高校学科(专业)拔尖人才学术资助重点项目(No: gxbjZD2016014)、安徽师范大学研究生科研创新与实践项目(2017cxsj045)和安徽省学术和技术带头人后备人选科研资助项目(2017H117)的资助。