损伤悬臂梁固有频率精确测量与分析

Measurement and Analysis of Natural Frequency of Damaged Cantilever Beam

摘要: 本文推导了悬臂梁损伤位置与结构损伤前后固有频率变化的关系，进而可计算悬臂梁损伤位置。为了减小悬臂梁固定端夹紧力波动对测量结果的影响，设计了一套具有较高精度的固有频率测量方法，并对该方法的精确性进行了实验验证，实验证明采用该方法可使固有频率测量值的平均相对误差降至0.7%以下。针对损伤前后悬臂梁的固有频率计算分析与测量，结果表明：通过固有频率变化得到出结构的损伤位置与实际位置基本一致。

Abstract: The relationship between the damage position of cantilever beam and the natural frequency change before and after structural damage is derived. In order to reduce the influence of the clamping force fluctuation of the fixed end of the cantilever beam on the measurement results, a set of natural frequency measurement method with high precision is designed. The accuracy of the method is verified by experiments. It is proved that the average relative error of the measured natural frequencies can be reduced to less than 0.7%. It calculated and analyzed the natural frequency of the cantilever beam before and after the damage. The results show that the damage position of the structure obtained by the natural frequency change is basically consistent with the actual position.

1. 引言

航空发动叶片的工作环境十分严苛，叶片发生断裂所导致的后果非常严重。因工况不同，发动机转子失效模式并不相同。其中最常发生的，危害最大的是转子叶片疲劳断裂失效 [1] 。航空发动机叶片的质量和性能直接影响整个飞机能否正常工作，因此准确检测航空发动机叶片的完整性和状态，提高发动机工作安全性，成为目前无损检测领域研究的一个共同热点 [2] 。基于振动理论可知，如果结构中存在损伤，结构系统中的动力学参数如质量、阻尼、刚度等都会发生相应改变，从而导致系统的振动模态和频响函数发生改变。固有频率是机械结构振动模态的最基本信息，是结构刚度与质量的函数，由于结构损伤的存在，导致结构的刚度减小、阻尼增大，固有频率就会有所降低 [3] 。对比结构损伤前后的固有频率变化情况，就能识别出结构是否存在损伤以及损伤大小情况 [4] 。Cawley和Adams [5] 基于利用结构损伤前后频率变化进行损伤识别的方法，得到了结构损伤前后任意两阶频率变化仅是损伤位置函数的结论。但是在实际测量固有频率时，固定端的夹紧力波动对测量结果影响很大 [6] 。因此在利用叶片的固有频率检测其损伤状态时，由于固定叶片的夹紧力不稳定，叶片的固有频率测量有较大的误差。在实际的测量中，叶片一般处于一端固定，另一端自由的悬臂状态。固定装置给叶根施加的夹紧力的大小对叶片固有频率测量结果有很大影响，当夹紧力变大时，固有频率测量结果相应也会变大。

详细描述利用固有频率推导悬臂梁的损伤位置的过程。针对叶片固有频率测量时夹紧力变化会影响测量结果的这一问题，设计了一套高精度固有频率测量方法和装置，并且对该方法的可靠性进行了实验验证。同时针对简化的叶片模型，对叶片损伤检测进行了验证。

2. 理论分析

对于一个多自由度结构系统，忽略阻尼的影响，其振动特征方程为：

$\left(K-{\omega }^{2}M\right)\phi =0$ (1)

式中，M为质量矩阵，K为刚度矩阵，ω为固有频率，φ为正则化振型。

当结构的刚度和质量发生微小变化∆K和∆M时，由摄动理论式(1)可知：

$\left[\left(K+\Delta K\right)-\left({\omega }^2+\Delta {\omega }^2\right)\left(M+\Delta M\right)\right]\left(\phi +\Delta \phi \right)=0$ (2)

结构的损伤对结构的刚度影响比较大，而对结构的质量影响比较小，一般当损伤比较小的时候可忽略质量的变化。由小损伤引起的振型变化也很小，所以忽略振型的变化 [7] 。将式(2)两边同时左乘φ^T，展开并且忽略质量的变化、振型的变化和高阶小量，则式(2)变为：

$\Delta {\omega }^2=\frac{{\phi }^{\text{T}}\Delta K\phi }{{\phi }^{\text{T}}M\phi }$ (3)

对于第i阶模态，式(3)有：

$\Delta {\omega }^2=\frac{{\phi }_i^{\text{T}}\Delta K{\phi }_i}{{\phi }_i^{\text{T}}M{\phi }_i}$ (4)

用∆K_n表示第n个单元的刚度变化，通常情况下， $\Delta K={\displaystyle \sum \Delta }{K}_n$ ,用 ${\epsilon }_n\left({\phi }_i\right)$ 表示由第阶振型 ${\phi }_i$ 计算得到的第n个单元的单元变形，则 ${\phi }_i^{\text{T}}\Delta K{\phi }_i$ 可表示为 ${\displaystyle {\sum }_n{\epsilon }_n^{\text{T}}\left({\phi }_i\right)\Delta K_n{\epsilon }_n\left({\phi }_i\right)}$ 将其带入式(4)得：

$\Delta {\omega }_i^2=\frac{{\displaystyle \underset{n}{\sum }{\epsilon }_n^{\text{T}}\left({\phi }_i\right)\Delta K_n{\epsilon }_n\left({\phi }_i\right)}}{{\phi }_i^{\text{T}}M{\phi }_i}$ (5)

当只有第n个单元出现损伤时，式(5)可简化为：

$\Delta {\omega }_i^2=\frac{{\epsilon }_n^{\text{T}}\left({\phi }_i\right)\Delta K_n{\epsilon }_n\left({\phi }_i\right)}{{\phi }_i^{\text{T}}M{\phi }_i}$ (6)

固有频率平方ω²的变化可定义为损伤位置n和损伤系数α_n的函数 [8] ，即：

$\Delta {\omega }_i^2={\lambda }_i\left({\alpha }_n,n\right)$ (7)

${\alpha }_n=\frac{\Delta K_n}{K_n}$ (8)

式中K_n为第n个单元的刚度矩阵，α_n为第n个单元的损伤系数，表示损伤的程度。由于通常单个损伤对刚度矩阵的各个单元影响不同，所以∆K_n/K_n一般是一个矩阵。但是通常结构单元损伤主要影响结构的一种刚度，因此α_n取标量。

把式(7)和式(8)带入式(6)，则可化为：

$\Delta {\omega }_i^2=\frac{{\alpha }_n{\epsilon }_n^{\text{T}}\left({\phi }_i\right)K_n{\epsilon }_n\left({\phi }_i\right)}{{\phi }_i^{\text{T}}M{\phi }_i}$ (9)

从式(9)可知，固有频率变化的平方是损伤位置和损伤程度的函数 [9] [10] 。取任意一阶固有频率变化的平方与第一阶固有频率变化的平方的比值的算数平方根，得到：

$$ (10)

式(10)表明，任意一阶固有频率变化与第一阶固有频率变化的比值的绝对值仅是结构损伤位置的函数。不同位置的损伤对应一组特定的固有频率变化比的绝对值，根据结构的损伤前后的各阶模态对应的频率变化比的绝对值，可识别出结构的损伤位置。为了精确地进行损伤定位，采用如式(11)所示的偏差函数的计算值作为损伤对位的依据：

$B={{\displaystyle \underset{i}{\sum }\left[{\left(\left|\frac{\Delta {\omega }_i}{\Delta {\omega }_1}\right|\right)}_O-{\left(\left|\frac{\Delta {\omega }_i}{\Delta {\omega }_1}\right|\right)}_C\right]}}^2$ (11)

式中下标O表示实验测试数据；C表示数值计算数据。

由式(11)可知，理想状态下，使B = 0的单元就是损伤所在单元。但在实际工程中，由于测量误差等原因，不可能使B = 0，一般可近似认为使B为最小值的单元，就是损伤所在单元。

3. 测量方法及装置

对于旋转机构，如在测试航空发动机转子叶片性能，当利用固有频率变化检测其损伤状况时，无法实现在线实时监测，需要将转子叶片拆下然后固定在其他夹具上进行测量。因普通夹具对转子叶片的夹紧力波动比较大，对所测得数据有较大的影响。为减小夹紧力变化对测量轻小构件固有频率造成的误差，在此提供一种测量装置及其方法，有效减小在多次拆卸安装时因夹紧力的变化而造成的误差，从而提高检测精度。

针对悬臂梁，其固定端为燕尾形榫头，提供一套测量方法和装置。各部件装配关系如下图1所示。

3.1. 原理及测量说明

3.1.1. 原理

消除夹紧力影响的装置如图1所示，利用螺栓顶紧垫片，然后通过垫片同时将被测件和参考件压紧，使其与夹具贴紧，实现固定。当其他条件不变时，悬臂梁的固有频率和夹紧力呈正相关。因此可用参考件的固有频率来表征夹具对悬臂梁的夹紧力的变化。当同一参考件固有频率不变时，即可认为被测件的夹紧力稳定不变。

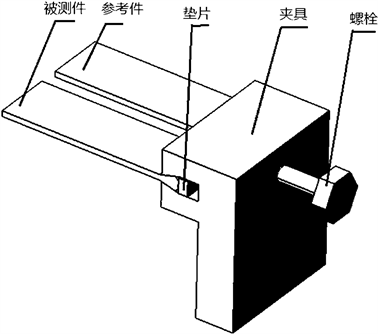
Figure 1. Measuring device and device assembly

图1. 测量装置及被测件装配图

3.1.2. 测量说明

在对被测件进行固有频率测量时，在所述装置上，同时固定与被测件相类似的参考件，如流程图2所示。选定适合的夹紧力固定参考件和被测件，然后测量参考件和被测件的初始固有频率，分别记为f_R和f_O。

规定当第i次测量， $\left|f_{Ri}-f_R\right|<m{f}_R$ 时，夹具的夹紧力稳定，测量数据有效，其中m为参考件固有频率允许变化范围。被测件经过一些处理或者变化后，需要再次测量固有频率时，同时固定被测件和参考件(被测件和参考件的固定位置要与第一次测量时候一致)，调节螺栓使参考件测得的固有频率f_Ri与初始固有频率f_R相对误差保持在允许范围内，然后测量被测件的固有频率，得到f_Oi。

3.2. 实验验证

对所述的测量方法及装置进行实验验证。以45号钢为材料，制作了上述测量装置以及被测件和参考件模型。实验将压电陶瓷贴在被测件和参考件上，进行扫频激励，用polytec PSV-500激光测振仪测量，如图3所示。

测量中，在参考件的固有频率基本不变的条件下，对被测件进行了多次安装–测量–拆卸的过程。测量中，通过调节螺栓控制夹紧力，使参考件第二阶固有频率稳定在适当的范围内，记录了实验数据如表1所示。

由表1中数据可知，当控制参考件第二阶固有频率平均相对误差小于0.07%时，可确保被测件第一阶和第二阶固有频率平均相对误差小于0.7%。综上所知：当保持参考件固有频率稳定在一定范围内时，被测件的固有频率具有较高的测量精度。

Figure 2. Measurement process

图2. 测量流程图

Figure 3. Experimental measurement

图3. 实验测量

Table 1. Measurement data of the test piece and reference piece without damage

表1. 无损伤时候被测件和参考件的测量数据

4. 利用固有频率变化对损伤悬臂梁分析

4.1. 对悬臂梁损伤处理

考虑悬臂梁承受载荷时，靠近固定端的地方所受应力最大，因此容易产生破坏。模拟悬臂梁产生疲劳裂纹，在靠近固定端的适当位置用钢锯制造一个宽1.3 mm，深1.4 mm的凹槽如下图4所示。

Figure 4. Damaged cantilever beam

图4. 产生损伤后的悬臂梁

4.2. 分析损伤悬臂梁的固有频率变化

4.2.1. 实验测量悬臂梁损伤前后频率变化

利用2.1所述的测量方法，测量损伤梁的固有频率。测量时按照表1所示测量结果，调节螺栓使参考件第二阶固有频率稳定在1934 Hz左右，然后测量损伤梁的前2阶固有频率，记录实验数据如表2所示范。由表1和表2可知，在该加持状态下，悬臂梁损伤后相比于损伤前其第一、二阶固有频率出现下降趋势。

Table 2. Natural frequency of damaged cantilever beam

表2. 损伤后悬臂梁固有频率

4.2.2. 有限元分析悬臂梁频率变化

利用COMSOL进行有限元分析。建立了相关的计算模型，按照物理场需要划分网格。计算出悬臂梁受损伤前第一阶和第二阶固有频率值分别为341 Hz和1985 Hz。损伤后第一阶和第二阶固有频率分别为307 Hz和1945 Hz。

在此基础上又分别计算了裂纹相对实际位置向右偏移不同距离时，第一阶和第二阶固有频率，并且根据式11计算B值，如表3所示。

由表3可知，裂纹位置与实际位置相同时，所计算得到的B值最小。当裂纹相对实际位置向左或向右偏移时，所计算的B值会呈现不同的上升趋势。因此可根据结构损伤前后固有频率变化初步估算裂纹位置。

Table 3. Natural frequency calculation of cracks at different positions

表3. 裂纹在不同位置时固有频率计算结果

5. 结论

1) 详细推导了悬臂梁损伤定位公式，得出了结构损伤前后固有频率变化的比值仅是损伤位置的函数。采用该方法可估算出只有单一损伤时悬臂梁损伤位置。

2) 制定了一套能够提高悬臂梁固有频率测量精度的方法。在实际工程应用中可减小由约束条件波动对测量结果造成的影响。对于文章所用试件，可将测量的平均相对误差控制在0.7%以下。

3) 制作了简化的航空发动机叶片模型。采用文章所述的测量方法和损伤定位公式，得到的损伤位置计算值与实际值一致。验证了损伤定位公式和固有频率测量方法的有效性。利用固有频率的变化计算结构的损伤位置具有定位简便，精度高，成本低的优点。

基金项目

江西省教育厅科学技术项目(DA201706712)。