测量反应堆反应性的费曼方法综述

Research Progress of Feynman Method to Measure Reactivity

摘要: 反应性是一个间接测量的参数，文章回顾总结了费曼方法进行反应性测量的基本原理及其物理意义。就该方法在反应堆临界时的发散，两次计数的时间间隔造成计数丢失效应，使用多个探测器测量进行数据综合，中子源释放相关的中子等新问题进行了分析讨论。对费曼方法应用时仍存在的问题提出了看法。

Abstract: Reactivity is a parameter measured indirectly. The principle and physical meaning of Feynman method to measure reactivity are reviewed in this paper. Some new problems such as the diver-gence while a reactor is at critical, the count loss effect due to time interval between count-ing-gates, data synthesis technique for several sensors, correlated neutron emitted by neutron source are discussed. Finally, the author’s own opinion is put forward upon the difficulty that still exists about application of Feynman method.

1. 引言

测量反应堆反应性的方差均值比方法最先是由费曼提出的，所以又叫费曼方法 [1] 。即使名义上的零功率反应堆，也仍然有大量的中子存在。堆中子统计规律的一个重要特点就是堆内中子不是完全互相无关的。

有些中子是由同一裂变链产生的，它们有着共同的“祖先”，在时间上有着相关性。如图1所示，中子a与中子b、c相关，与中子d不相关。这种相关性的存在，使得中子探测器计数率的统计特性偏离了泊松分布。

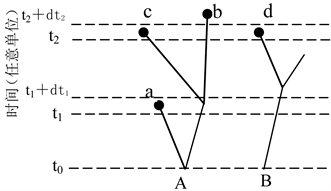
Figure 1. Diagram of neutron fission chain

图1. 中子裂变链示意图

将缓发中子看作是相互独立无关的，和一般的外中子源一样是服从泊松分布的本底，忽略缓发中子之间的相关性，则中子计数的方差与平均值之比为 [1]

$\frac{{\sigma }^2}{m}=1+\frac{\epsilon D_v}{{\rho }_p^2}\left(1-\frac{1-{\text{e}}^{-\alpha T}}{\alpha T}\right)=1+Y$ (1)

其中， $D_v=\frac{\overline{v\left(v-1\right)}}{{\bar{v}}^2}$ ，v为每次裂变产生的中子数， $\epsilon$ 是探测器的效率，T为测量统计时间， $\alpha$ 为瞬发中子衰减常数， ${\rho }_p$ 为瞬发反应性。

对于完全随机不相关的中子，它们的统计特性服从泊松分布，其方差与平均值之比为1，即 $Y=0$ 。若中子探测器在某个时刻的计数可能与以前的计数是相关的，即某个时刻引起计数的中子与以前引起计数的中子是属于同一个裂变链，则 $Y>0$ 。所以Y代表的是堆内中子相关部分，即为堆内中子统计特性偏离泊松分布程度的测度。

对于不同的统计时间T测量出对应的Y，然后利用最小二乘法可以得到瞬发中子衰减常数 $\alpha$ 。根据 $\alpha =\frac{\beta -\rho }{l}$ ，得到反应性 $\rho$ 。其中l是瞬发中子平均寿命， $\beta$ 是缓发中子份额。

对于以U²³⁵为燃料的热中子水堆，统计时间T一般在<10 ms的范围内选择，如10 ms、5 ms、1 ms、0.5 ms、0.1 ms等 [2] 。

当考虑缓发中子的衰减过程，分析缓发中子存在的互相关中子，则相关中子测度Y为 [3]

$Y=\epsilon D_v{\displaystyle \underset{i=1}{\overset{7}{\sum }}\frac{2A_i}{{\alpha }_i}{H}_0\left({\alpha }_i\right)\left(1-\frac{1-{\text{e}}^{-{\alpha }_{i}T}}{{\alpha }_{i}T}\right)}$ (2)

$A_i$ 、 ${\alpha }_i$ 由下面的零功率传递函数决定，

$H_0\left(s\right)={\displaystyle \underset{i=1}{\overset{7}{\sum }}\frac{A_i}{{\alpha }_i+s}}$

决定。文献 [4] 试验检测了缓发中子对中子相关测度Y的影响。

测量反应性的Feynman方法提出的时间应该说比较久远了，但是随着应用的不断深入，人们发现了一些新的问题，并着力进行了研究。

2. 临界发散的问题

当反应堆临界时，零功率传递函数的最后一个极点 ${\alpha }_7$ 为零，方差均值比表达式(2)会出现发散。Bennet [3] [5] [6] 提出如下方法来测量堆内中子相关程度，以避免临界时发散的问题。

$\frac{\langle {\left(c_{k+1}-c_k\right)}^2\rangle }{2\langle c_k\rangle }=1+W$ (3)

其中 $W={\displaystyle \underset{i=1}{\overset{7}{\sum }}{H}_0\left({\alpha }_i\right)\left(1-\frac{\frac{3}{2}+\frac{1}{2}{\text{e}}^{-2{\alpha }_{i}T}-2{\text{e}}^{-{\alpha }_{i}T}}{{\alpha }_{i}T}\right)}$ ，

$\langle \cdot \rangle$ 表示均值， $c_k$ 为第k个时间间隔T内的计数，W反映了堆内中子相关程度。

Wallerbos [7] 发现由于试验测量时间是有限的，实际试验中相关中子测度Y并不会发散，提出了修正后的有限测量时间模型

$\langle Y\left(NT\right)\rangle =2\epsilon D_v{\displaystyle \underset{i=1}{\overset{7}{\sum }}\frac{A_i}{{\alpha }_i}{H}_0\left({\alpha }_i\right)}\times \left[f\left({\alpha }_{i}T\right)-\frac{1}{N}f\left({\alpha }_{i}NT\right)\right]$ (4)

NT为测量时间， $f\left(T\right)=1-\frac{1-{\text{e}}^{-\alpha T}}{\alpha T}$ 。如果测量时间无限， $N\to \infty$ ，则 $Y\left(T\right)$ 的期望值

$\underset{N\to \infty }{\lim }\langle Y\left(NT\right)\rangle =2\epsilon D_v{\displaystyle \underset{i=1}{\overset{7}{\sum }}\frac{A_i}{{\alpha }_i}{H}_0\left({\alpha }_i\right)f\left({\alpha }_{i}T\right)}$

与(2)式完全一致。当反应堆临界时，零功率传递函数的最后一个极点 ${\alpha }_7$ 为零，表达式(2)发散。而将函数 $f\left(T\right)$ 进行泰勒展开取前两阶

$\underset{x\to 0}{\lim }f\left(x\right)=\frac{1}{2}x-\frac{1}{6}{x}^2$

代入有限测量时间模型(4)的零极点项，有

$\underset{{\alpha }_7\to 0}{\lim }\frac{A_7}{{\alpha }_7}{H}_0\left({\alpha }_7\right)\left[f\left({\alpha }_{7}T\right)-\frac{1}{N}f\left({\alpha }_{7}NT\right)\right]=\frac{1}{12}{A}_7^2\left(N-1\right)T^2$

可以看出反应堆临界时，方差均值比随着测量时间NT的增长而增加，除非测量时间无限，否则不会发散。Wallerbos在瑞士Paul Scherrer学院的HTR-PROTEUS试验装置上进行了试验验证 [8] 。测量统计时间NT在60 ms至6 s范围内， $Y\left(NT\right)$ 试验值与理论计算值很接近，反应性的测量值与脉冲中子源法也相当吻合。

3. 计数时间间隔效应

两次中子计数之间不可避免存在一个时间间隔 $\Delta$ [9] ，如图2所示，造成计数丢失。

Figure 2. Diagram of count time interval

图2. 计数时间间隔示意图

如果 $\Delta$ 不可忽略，Yamane如下定义了这种情况下的均值和均方值

$\bar{c}={\displaystyle \underset{i=1}{\overset{N}{\sum }}{c}_i}$ ， $\overline{c^2}={\displaystyle \underset{i=1}{\overset{N}{\sum }}\overline{c_i^2}}+2{\displaystyle \underset{i<j}{\sum }\overline{c_i{c}_j}}$

由此建立了考虑时间间隔 $\Delta$ 后计算相关中子测度Y的方法 [10]

$\begin{array}{c}Y\left(NT\right)=2\epsilon D_v{\displaystyle \underset{i=1}{\overset{7}{\sum }}\frac{A_i}{{\alpha }_i}{H}_0\left({\alpha }_i\right)}[1-\frac{1-{\text{e}}^{-{\alpha }_{i}T}}{{\alpha }_{i}T}+\frac{{\left(1-{\text{e}}^{-{\alpha }_{i}T}\right)}^2}{{\alpha }_{i}T}\\ \times {\displaystyle \underset{j=1}{\overset{N}{\sum }}\frac{N-j}{N}}\exp \left(-{\alpha }_i\left(j\Delta +j-1\right)T\right)]\end{array}$ (5)

符号含义同前。当 $\Delta =0$ 时，Yamane验证了式(5)与式(2)保持一致。Wallerbos [11] 在HTR-PROTEUS试验装置上的试验表明，两次中子计数之间时间间隔 $\Delta =2\text{ms}$ 时， $Y\left(NT\right)$ 试验值与理论计算值相当吻合。Kitamura [12] 在京都大学的临界装置KUCA上的试验表明，当 $\Delta$ 与每次计数时间T之比从0变化至100%的情况下，利用式(5)都能很好地实现反应性的测量。

4. 使用多个探测器的问题

如果同时使用多个探测器进行反应性测量，测量采集的数据如何进行综合呢？Yamane从主方程出发，引入几率母函数，提出了这种情况下计算相关中子测度Y的方法 [13]

$\begin{array}{c}{Y}_{syn}\left(T\right)=\left(\frac{1}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\epsilon }_{i}D\left(d_i\right)}}\right)\{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\epsilon }_i^2{D}^2\left(d_i\right)}\times \left[QT\left(2-\frac{d_i}{T}\right)\left(-\frac{d_i}{T}\right)+A\left(1-\frac{d_i}{T}\right){\text{e}}^{-\alpha d_i}f\left(T-d_i\right)\right]\\ +2{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=i+1}{\overset{n}{\sum }}{\epsilon }_i{\epsilon }_{j}D\left(d_i\right)D\left(d_j\right)Af\left(T\right)}}\}\end{array}$ (6)

n为探测器的个数， $A=\frac{\overline{v\left(v-1\right)}}{{\alpha }^2{\tau }_f^2}$ ， $f\left(T\right)=1-\frac{1-{\text{e}}^{-\alpha T}}{\alpha T}$ ，Q为裂变率， ${\tau }_f$ 为发生一次裂变的平均时间， $D\left(d_i\right)$ 是关于不灵敏时间 $d_i$ 的函数，其余符号含义同前。Yamane讨论了n个探测器的效率 ${\epsilon }_i$ 和不灵敏时间 $d_i$ 都相同均为 $\epsilon$ 和d的情形，假设不灵敏时间d与测量时间T之比 $d/T$ 很小， $f\left(T-d\right)$ 几乎等于 $f\left(T\right)$ ，则(6)简化为

$Y_{syn}\left(T\right)=-2\epsilon D\left(d\right)Qd+n\epsilon D\left(d\right)A\left(1-\frac{1-{\text{e}}^{-\alpha T}}{\alpha T}\right)$ 不考虑不灵敏时间效应， $d=0$ ， $D\left(d_i\right)=1$ ，进一步简化为

$Y_{syn}\left(T\right)=n\epsilon A\left(1-\frac{1-{\text{e}}^{-\alpha T}}{\alpha T}\right)$ (7)

与式(2)仍然保持一致。

5. 中子源释放相关中子

以上分析的各种情况都是假设使用传统的中子源，如Am-Be，Po-Be等，通过衰变射线在靶核上引起中子发射，每次事件只释放一个中子。每次事件释放的中子相互独立，堆内中子的相关性仅仅来源于同一裂变链上中子的相关性。

随着对加速器驱动次临界系统(Accelerator Driven Sub-critical System ADS)的研究越来越多，研究者尝试将Feynman方法应用于ADS，并发现了新的问题。

加速器驱动次临界系统包括中能质子加速器、外源中子产生器和次临界反应堆。加速器加速的质子轰击重金属靶(如铅)与靶核发生散裂反应，1个质子引起的散裂反应可产生几十个中子。用散裂中子作为外中子源作用于次临界反应堆上。

因此加速器驱动次临界系统中子源的特点是每次释放的中子数不只一个，增加了一个堆内中子数涨落的因素。对于自发裂变中子源²⁵²Cf也是这样。堆内中子的相关性不仅来源于同一裂变链上中子的相关性，而且来源于中子源同一次事件(ADS的散裂反应或²⁵²Cf的自发裂变)产生的中子之间的相关性。

中子源Am-Be，Po-Be等，一次事件释放一个中子，中子源释放的中子服从泊松分布。使用²⁵²Cf作为中子源的反应堆(有的反应堆是使用²⁵²Cf正比计数管，²⁵²Cf正比计数管既做中子探测器，又做中子源)，²⁵²Cf一次自发裂变释放1~8个中子，中子源释放的中子服从复合泊松分布。由加速器驱动的中子源，1个质子引起的散裂反应可产生几十个中子，中子源释放的中子同样服从复合泊松分布。

假设 $p\left(t_1,t_2\right)$ 是在 $\left(t_1,t_1+\text{d}{t}_1\right)$ 和 $\left(t_2,t_2+\text{d}{t}_2\right)$ 时间间隔内都探测到一个中子的几率，有

$\begin{array}{c}p\left(t_1,t_2\right)=p_{corr}\left(t_1,t_2\right)+p\left(t_1\right)p\left(t_2\right)\\ =p_{c,f}\left(t_1,t_2\right)+p_{c,s}\left(t_1,t_2\right)+p\left(t_1\right)p(t2)\end{array}$

$p_{c,f}\left(t_1,t_2\right)$ 表示由同一裂变链引起中子相关的几率， $p_{c,s}\left(t_1,t_2\right)$ 表示由中子源引起中子相关的几率， $p\left(t_1\right)$ 、 $p\left(t_2\right)$ 分别是在 $\left(t_1,t_1+\text{d}{t}_1\right)$ 和 $\left(t_2,t_2+\text{d}{t}_2\right)$ 时间间隔内各自独立探测到一个中子的几率。在不考虑缓发中子效应时，Pazsit得到了此时计算相关中子测度Y的方法 [14]

$Y\left(T\right)=\epsilon D_v\frac{1}{{\rho }^2}\left(1+\delta \right)\left(1-\frac{1-{\text{e}}^{-\alpha T}}{\alpha T}\right)$ (8)

其中， $\delta =\frac{\bar{q}{D}_q}{\bar{v}{D}_v}$ ， $D_q=\frac{\overline{q\left(q-1\right)}}{{\bar{q}}^2}$ ，q为中子源每次事件释放的中子数，其余符号同前。与(1)式比较，可以看出由于中子源引起的相关中子的存在，使得中子相关部分的测度 $Y\left(T\right)$ 增大了，这对于反应性测量是有利的。

6. 小结

对利用Feynman方法进行反应性测量的半个多世纪来的文献资料分析总结表明，国内外研究人员对Feynman方法做了持续不懈的研究。针对理论分析和实验过程中碰到的一些新问题，努力提出了解决方法。并利用研究装置或采用蒙特卡罗方法检验处理过程中的假设是否合理、方法是否有效。

关于测量不灵敏时间问题的处理存在不小的分歧，不论采用基于Markov过程的方法 [15] [16] [17] [18] [19] 还是相关滤波技术的方法 [5] [20] [21] [22] ，分析过程和结论都十分复杂，这应该是式(6)中的不灵敏时间函数未能显式表示的原因 [13] 。而且由于计算机技术的快速发展，传统的多道分析仪可以使用高速数据采集卡来代替。