1. 引言
船舶振动及所引起的噪声,不仅影响船舶人员工作环境和居住舒适性,更会使船体结构产生疲劳破坏,影响船舶的安全性和隐身性。传统钢制船舶在船舶减振降噪性能方面往往无法满足实际需要的要求,相比之下,朱竑祯提出的新型阻尼材料、新型复合材料等众多结构优化而形成的新型材料 [1],在材料特性性能等方面表现更佳。其中,复合材料由于具有阻尼性能好、比强度大、比刚度高、材料可设计性强、耐腐蚀、成型方便等优点,在船体轻量化与减振降噪方面具有良好的应用前景。此外,机械噪声是各种船舶水下噪声的重要成分 [2],人们通常采用隔振及阻尼减振等措施对已有船舶的水下噪声进行控制 [3]。
无论是船体结构声学设计还是采用减振降噪措施,都需要对船体振动噪声性能进行科学预报。在进行船舶振动噪声分析时,由于船体结构大而复杂,难以用解析方法进行求解,相比而言,数值计算为解决工程减振降噪技术提供了可行方案。大型结构的复杂部件在材料、几何属性和声振特性等方面是不同的,因此在动力学分析过程中,往往根据结构不确定性对自身的动态特性的影响将其分为中低频、高频两频段进行计算。数值计算方面,国内外研究者的惯例为采用有限元方法对船体中低频振动进行仿真,而采用能量统计方法对船体高频振动进行数值计算 [4] [5] [6]。
本文提出一种船舶振动噪声数值预报方法,对相同型线的复合材料船和钢制船的振动噪声性能进行研究,通过量化指标对比研究,证实了复合材料在船舶减振降噪技术方面的优势,为提升船舶安静型和舒适性提供理论依据。
2. 数值方法
2.1. 低频工况数值计算模型
船体结构主要参数如表1所示。
利用ABAQUS软件对主船体及上层建筑结构进行了有限元建模。建模时主要考虑了船体外板、舱壁、甲板和平台、主要支撑构件、上层建筑等主要结构部件,其中船底板、舷侧板、甲板板、舱壁板以及上层建筑板采用四节点S4R壳体单元模拟,加强筋采用B31梁单元模拟,结构单元总体尺寸约为47 mm,局部过渡区域采用精细化网格进行过渡,保证网格划分精度。模型一共划分75,864个节点,83,009个单元。根据实际建模过程,计算模型的X方向为沿船体纵向,Y方向为沿船体横向,Z方向为沿船体垂向。总体有限元模型见图1。

Figure 1. Overall finite element model of the hull structure
图1. 船体结构总体有限元模型
材料考虑复合材料和钢材两种,其中复合材料船体材料性能参数设置表2所示,钢船材料性能参数设置表3所示:

Table 2. Performance parameters of composite hull materials
表2. 复合材料船体材料性能参数

Table 3. Mechanical properties of steel
表3. 钢材力学性能
2.2. 高频工况数值计算模型
高频振动模型由基于统计能量方法的VAONE软件建立,并进行单位激励力下的高频振动响应计算,如下图所示,每个板都是一个统计能量单元,在各相邻的统计能量单元之间建立连接,允许单元之间的能量流动,甲板等有正交加强筋的平面,面上的加强筋用软件中的加筋板功能设置。各统计能量单元之间的连接示意图如图2所示。
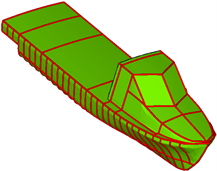
Figure 2. Connections between various statistical energy units
图2. 各个统计能量单元之间的连接
2.3. 数值计算设置
低频振动有限元计算时,分别在复合材料船体基座和钢船船体基座相同位置施加垂直于面板的单位激励力,如图3所示。采用直接法进行谐响应分析,有限元计算频率范围为20 Hz~500 Hz,计算频率间隔为1 Hz。通过计算,分别获得基座输入点(激励点)和壳体输出点的振动加速度响应,并进行数据处理分析。高频振动有限元计算时,同样分别在复合材料船体基座和钢船船体基座相同位置施加垂直于面板的单位激励力,如图4所示。

Figure 3. The position of the ship’s excitation force
图3. 钢船激励力施加位置示意图
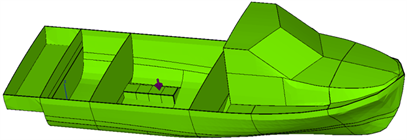
Figure 4. Schematic diagram of hull high-frequency excitation load application position
图4. 船体高频激励载荷施加位置示意图
3. 结果及分析
3.1. 船体不同位置振动噪声分析
首先研究了船体不同测点选取对比计算结果。对于振动响应输出点,复合材料船和钢船测点位置以及数目均选取一致,以便于对比。选取的测点分为两组:
1) 一组主要分布在激励点的基座周围,一共选取4圈,沿着船底、舷侧以及甲板均匀选取,每圈6个共24个测点,如图5(a)所示;
2) 一组沿全船分布,一共选取6圈,沿着船底、舷侧以及甲板均匀选取,每圈6个共36个测点,如图5(b)所示。
以复合材料船舶为例进行分析,在单位激振力作用下,采用有限元计算得到的在20 Hz~500 Hz频段范围内,复合材料船体输出点平均输出振动响应的对比如图6所示。采用统计能量法求得的复合材料船激励点周围测点板的高频振动响应结果,如图7所示。由对比可知:激励点周围测点的平均振动响应在全频段均高于全船分布测点的平均振动响应,从二者低频1/3倍频程总级比较结果来看,激励点周围测点的平均总振级高于全船分布测点3.7 dB,高频总振级也出现在激振点位置,说明振动能量主要集中传递到激励点周围的船壳结构上。随着离激励点的距离增加,振动响应逐渐减小。后面计算时,主要分析激励点周围测点的平均振动响应。
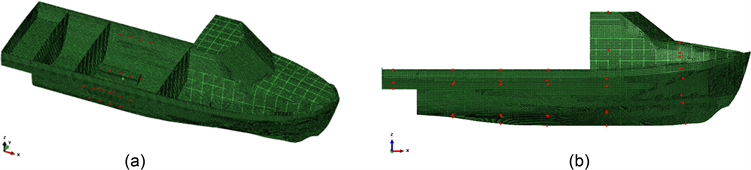
Figure 5. Schematic diagram of measuring points. (a) Schematic diagram of point 1; (b) Schematic diagram of point 2
图5. 测点示意图。(a) 输出测点1选取示意图;(b) 输出测点2选取示意图
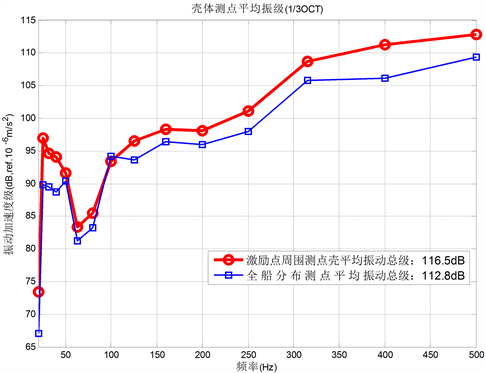
Figure 6. Calculation result of low frequency vibration response
图6. 低频振动响应计算结果
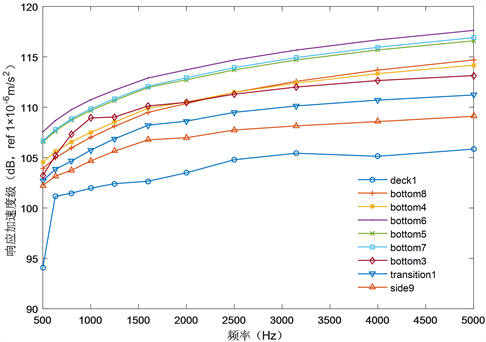
Figure 7. Calculation result of high frequency vibration response
图7. 高频振动响应计算结果
3.2. 不同材质船舶振动噪声性能分析
钢船一节振动模态和扭转振动模态如图8,图9所示。钢船一阶模态频率约在10.5 Hz,为上层建筑后端壁板的局部振动;一阶整体弯曲振动频率约在44.7 Hz。
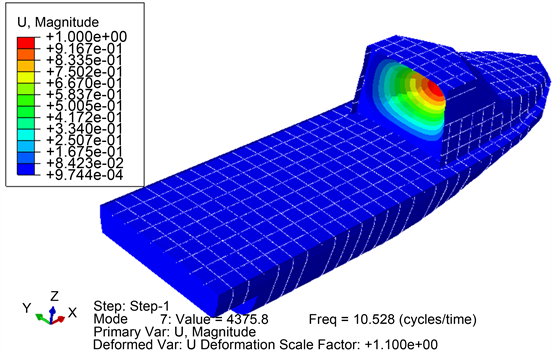
Figure 8. First-order vibration mode of a steel ship
图8. 钢船一阶振动模态
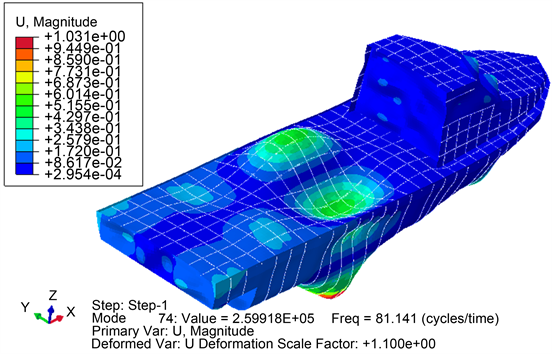
Figure 9. Torsional vibration mode of steel ship main hull
图9. 钢船主船体扭转振动模态
对比分析了采用有限元方法获得的在20 Hz~500 Hz频段范围内,在船体基座相同位置单位力激励下,复合材料船与钢船壳体的平均输出振动结果,其1/3倍频程带级的比较结果分别如图10所示。在采用有限元法及统计能量法计算得到的20 Hz~5k Hz频段范围内壳体测点1/3倍频程结果的对比,如图11所示。
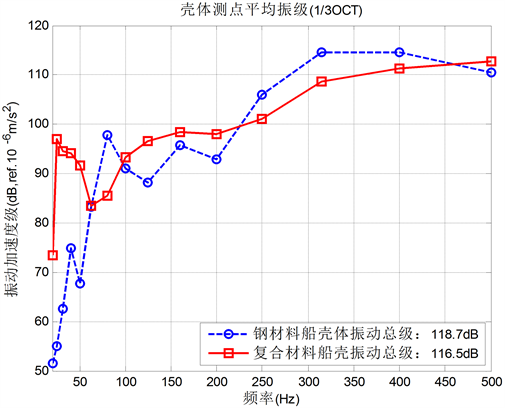
Figure 10. Comparison of average hull vibration levels (20~500 Hz)
图10. 船壳平均振级对比(20~500 Hz)
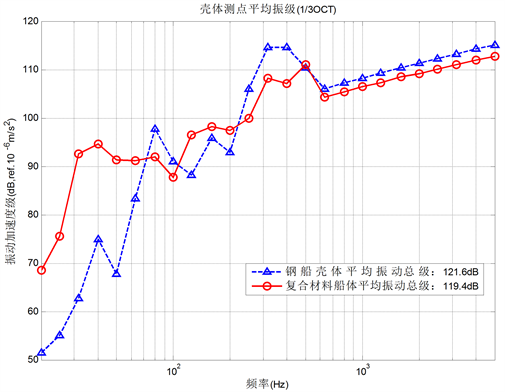
Figure 11. Comparison of average hull vibration levels (20~500 Hz)
图11. 船壳平均振级对比(20~500 Hz)
在20 Hz~500 Hz频段,复合材料船壳与钢船测点平均振动响应的1/3倍频程对比结果可知:复合材料船在230 Hz~447 Hz频段范围内平均振动响应小于钢船壳体,具有一定的减振效果;从1/3倍频程总级比较结果来看,在20 Hz~500 Hz的中、低频段,复合材料船相对钢船减振降噪效果为2.2 dB。在20 Hz~5k Hz全频段,振动频率较低时,钢船的减振降噪性能优于复合材料船舶,但全频段来看,复合材料船相对钢船减振降噪效果也为2.2 dB,复合材料船减振降噪效果优于钢质船舶。
4. 结论
本文提出了一种结合有限元方法和统计能量方法的船舶振动噪声数值评估方法,对船舶的低频和高频振动区分考虑,实现对船舶减振降噪性能进行有效分析。采用该方法,对相同型线的复合材料船和钢制船的振动噪声性能进行研究,通过量化指标来对比研究复合材料和传统材料在船舶减振降噪方面不同,总的来看,复合材料船舶的减振降噪效果优于钢制船舶。
基金项目
山东省重点研发计划(军民科技融合),2016JMRH0539。
NOTES
*通讯作者。